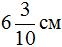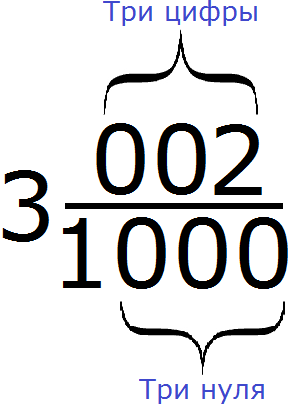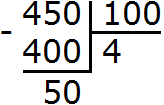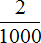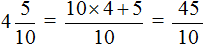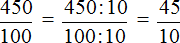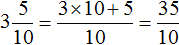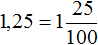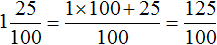Для чего нужны десятичные дроби

Исследования учащихся по теме Кому и зачем нужны десятичные числа

Содержание

Тема исследования

Какие действия можно производить с десятичными дробями

Актуальность проблемы

Расширение понятия числа и появление новых видов связей между числами, всевозможных способов выполнения различных действий с данными числами.

Выяснить какие действия можно производить с десятичными дробями, кому и зачем они нужны, и можно ли стать успешным в жизни, не зная теории чисел.

Задачи

Рассмотреть десятичные дроби со следующих точек зрения:

Гипотеза

Предполагаем, что в жизни мы можем обойтись без десятичных дробей, используя другие числа.

Этапы исследования

1. Определение проблемы и вытекающих из нее задач исследования.

2. Выдвижение гипотезы их решения.

3. Обсуждение методов исследования.

4. Поиск теоретической информации.

5. Подбор примеров к каждому разделу теории.

6. Оформление результатов поиска в виде презентации.

7. Подведение итогов.

Объект исследования

Методы

1. Эмпирические: наблюдение и опрос(анкетирование учащихся,сбор информации по различным источникам)

2. Теоретические: анализ и синтез( анализ промежуточных исследований)

Ход работы

1. Поиск различных источников информации по теме.

2. Анализ найденной информации и составление конспекта по теме.

3. Создание дидактических материалов по теме.

4. Представление результата в виде презентации.

Наши результаты

1.Защита исследовательской работы на уроке.

2.Отчетная презентация по исследовательской работе.

3.Тематическая газета к предметной неделе в школе.

Выводы

Список ресурсов

Источник

ДЕСЯТИЧНАЯ ДРОБЬ

Ключевые слова конспекта: десятичная дробь, сравнение дробей, арифметические действия с дробями, нахождение части от целого и целого по его части, представление десятичной дроби в виде обыкновенной и обыкновенной в виде десятичной.

Дробные числа, знаменатель которых равен 10, 100, 1000 и т. д., можно записать не только в виде обыкновенных, но и в виде десятичных дробей.

Сравнение десятичных дробей

Арифметические действия с десятичными дробями

Сложение и вычитание десятичных дробей

Чтобы сложить (вычесть) десятичные дроби, нужно:

Умножение десятичных дробей

При умножении десятичных дробей сначала нужно выполнить умножение, не обращая внимания на запятую, а затем в произведении отделить запятой справа столько знаков, сколько их имеется после запятой в обоих множителях вместе.

Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001, нужно перенести запятую влево на сколько цифр, сколько нулей стоит перед единицей в множителе.

Деление десятичных дробей

Чтобы разделить десятичную дробь на натуральное число, нужно:

Чтобы разделить десятичную дробь на 10, 100, 1000, …, нужно перенести влево запятую в этой дроби на сколько цифр, сколько нулей стоит после единицы в делителе.

Чтобы разделить число на десятичную дробь, нужно:

Чтобы разделить десятичную дробь на 0,1; 0,01; 0,001, нужно перенести в ней запятую вправо на столько цифр, сколько нулей стоит в делителе перед единицей (т. е. умножить дробь на 10, 100, 1000, …).

Представление десятичной дроби в виде обыкновенной
и обыкновенной в виде десятичной

Чтобы обратить десятичную дробь в обыкновенную, достаточно в числителе дроби записать число, стоящее после запятой, а в знаменателе — единицу с нулями, причем нулей должно быть столько, сколько цифр справа от запятой. Если можно, дробь сократить.

Чтобы обратить обыкновенную дробь в десятичную, следует разделить числитель на знаменатель по правилу деления десятичной дроби на целое число.

Не каждую обыкновенную дробь можно перевести в десятичную. Если знаменатель обыкновенной дроби не содержит простых множителей, кроме 2 и 5, то эту обыкновенную дробь можно перевести в десятичную.

Учитывая это правило, можно переводить обыкновенную дробь в десятичную не с помощью деления, а приведением ее к знаменателю 10, 100, 1000 путем умножения числителя и знаменателя этой дроби на недостающие множители.

Это конспект по теме «Десятичная дробь». Выберите дальнейшие действия:

Источник

Десятичные дроби

Мы уже говорили, что дроби бывают обыкновенные и десятичные. На данный момент мы немного изучили обыкновенные дроби. Мы узнали, что обыкновенные дроби бывают правильные и неправильные. Также мы узнали, что обыкновенные дроби можно сокращать, складывать, вычитать умножать и делить. И ещё мы узнали, что бывают так называемые смешанные числа, которые состоят из целой и дробной части.

Мы ещё не до конца изучили обыкновенные дроби. Есть немало тонкостей и деталей, о которых следует поговорить, но уже сегодня мы начнём изучать десятичные дроби, поскольку обыкновенные и десятичные дроби достаточно часто приходится сочетать. То есть при решении задач приходиться работать с обоими видов дробей.

Этот урок возможно покажется сложным и непонятным. Это вполне нормально. Такого рода уроки требуют, чтобы их именно изучали, а не просматривали поверхностно.

Выражение величин в дробном виде

Иногда удобно бывает показать что-либо в дробном виде. Например, одна десятая часть дециметра записывается так:

Это выражение означает, что один дециметр был разделён на десять равных частей, и от этих десяти частей была взята одна часть. А одна часть из десяти в данном случае равна одному сантиметру:

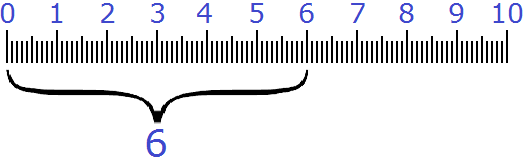
Рассмотрим следующий пример. Пусть требуется показать 6 см и ещё 3 мм в сантиметрах в дробном виде.

Итак, 6 целых сантиметров у нас уже есть:

Но осталось еще 3 миллиметра. Как показать эти 3 миллиметра, при этом в сантиметрах? На помощь приходят дроби. Один сантиметр это десять миллиметров. Три миллиметра это три части из десяти. А три части из десяти записываются как 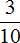см

Выражение 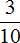см означает, что один сантиметр был разделён на десять равных частей, и от этих десяти частей взяли три части.

В результате имеем шесть целых сантиметров и три десятых сантиметра:

Дроби, в знаменателе которых присутствуют числа 10, 100, 1000 можно записывать без знаменателя. Сначала пишут цéлую часть, а потом числитель дробной части. Целая часть отделяется от числителя дробной части запятой.

Например, запишем 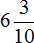без знаменателя. Сначала записываем целую часть. Целая часть это 6

Целая часть записана. Сразу же после написания целой части ставим запятую:

И теперь записываем числитель дробной части. В смешанном числе 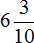числитель дробной части это число 3. Записываем после запятой тройку:

Любое число, которое представляется в таком виде, называется десятичной дробью.

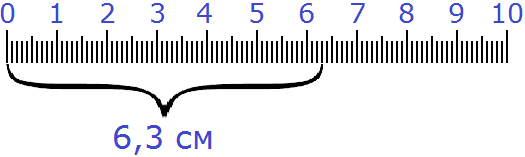
Поэтому показать 6 см и ещё 3 мм в сантиметрах можно с помощью десятичной дроби:

Выглядеть это будет следующим образом:

На самом деле десятичные дроби это те же самые обыкновенные дроби и смешанные числа. Особенность таких дробей заключается в том, что в знаменателе их дробной части содержатся числа 10, 100, 1000 или 10000.

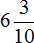
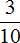
Как и смешанное число, десятичная дробь имеет цéлую часть и дробную. Например, в смешанном числе целая часть это 6, а дробная часть это .

В десятичной дроби 6,3 целая часть это число 6, а дробная часть это числитель дроби 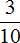, то есть число 3.

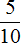
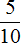
Бывает и так, что обыкновенные дроби в знаменателе которых числа 10, 100, 1000 даны без целой части. Например, дробь дана без целой части. Чтобы записать такую дробь как десятичную, сначала записывают 0, затем ставят запятую и записывают числитель дробной части. Дробь без знаменателя будет записана следующим образом:

Читается как «ноль целых, пять десятых».

Перевод смешанных чисел в десятичные дроби

Когда мы записываем смешанные числа без знаменателя, мы тем самым перевóдим их в десятичные дроби. При переводе обыкновенных дробей в десятичные дроби нужно знать несколько моментов, о которых мы сейчас поговорим.

После того как записана целая часть, обязательно нужно посчитать количество нулей в знаменателе дробной части, поскольку количество нулей дробной части и количество цифр после запятой в десятичной дроби должно быть одинаковым. Что это значит? Рассмотрим следующий пример: перевести смешанное число 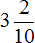в десятичную дробь.

Сначала записываем целую часть и ставим запятую:

И можно бы сразу записать числитель дробной части и десятичная дробь готова, но обязательно нужно посчитать сколько нулей содержится в знаменателе дробной части.

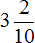
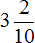
Итак, посчитаем количество нулей в дробной части смешанного числа . Видим, что в знаменателе дробной части один ноль. Значит в десятичной дроби после запятой будет одна цифра и это цифра будет числитель дробной части смешанного числа , то есть число 2

Таким образом, смешанное число 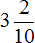при переводе в десятичную дробь обращается в 3,2. Эта десятичная дробь читается так:

«Три целых, две десятых»

«Десятых» потому что в дробной части смешанного числа 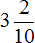содержится число 10.

Пример 2. Перевести смешанное число 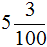в десятичную дробь.

Записываем цéлую часть и ставим запятую:

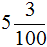
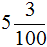
И можно бы сразу записать числитель дробной части и получить десятичную дробь 5,3 но правило говорит, что после запятой должно быть столько цифр сколько нулей в знаменателе дробной части смешанного числа . А мы видим, что в знаменателе дробной части два нуля. Значит в нашей десятичной дроби после запятой должно быть две цифры, а не одна.

В таких случаях числитель дробной части нужно немного видоизменить: добавить ноль перед числителем, то есть перед числом 3

Теперь можно довести дело до конца. Записываем после запятой числитель дробной части:

Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа 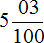одинаково.

Десятичная дробь 5,03 читается так:

«Пять целых, три сотых»

«Сотых» потому что в знаменателе дробной части смешанного числа 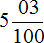содержится число 100.

Пример 3. Перевести смешанное число 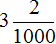в десятичную дробь.

Из предыдущих примеров мы узнали, что для успешного перевода смешанного числа в десятичную дробь, количество цифр в числителе дробной части и количество нулей в знаменателе дробной части должно быть одинаковым.

Перед переводом смешанного числа 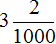в десятичную дробь, его дробную часть нужно немного видоизменить, а именно сделать так, чтобы количество цифр в числителе дробной части и количество нулей в знаменателе дробной части было одинаковым.

В первую очередь смóтрим на количество нулей в знаменателе дробной части. Видим, что там три нуля:

Наша задача организовать в числителе дробной части три цифры. Одна цифра у нас уже есть — это цифра 2. Осталось добавить ещё две цифры. Ими будут два нуля. Добавим их перед цифрой 2. В результате количество нулей в знаменателе и количество цифр в числителе станет одинаковым:

Теперь можно заняться переводом этого смешанного числа в десятичную дробь. Записываем сначала цéлую часть и ставим запятую:

и сразу записываем числитель дробной части

Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа 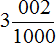одинаково.

Десятичная дробь 3,002 читается так:

«Три целых, две тысячных»

«Тысячных» потому что в знаменателе дробной части смешанного числа 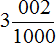содержится число 1000.

Перевод обыкновенных дробей в десятичные дроби

Обыкновенные дроби, у которых в знаменателе числа 10, 100, 1000 или 10000, тоже можно перевести в десятичные дроби. Поскольку у обыкновенной дроби целая часть отсутствует, сначала записывают 0, затем ставят запятую и записывают числитель дробной части.

Здесь также количество нулей в знаменателе и количество цифр в числителе должно быть одинаковым. Поэтому следует быть внимательным.

Пример 1. Перевести обыкновенную дробь 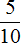в десятичную дробь.

Целая часть отсутствует, значит сначала записываем 0 и ставим запятую:

Теперь смóтрим на количество нулей в знаменателе. Видим, что там один ноль. И в числителе одна цифра. Значит можно спокойно продолжить десятичную дробь, записав после запятой цифру 5

В полученной десятичной дроби 0,5 количество цифр после запятой и количество нулей в знаменателе дроби 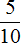одинаково. Значит дробь переведена правильно.

Десятичная дробь 0,5 читается так:

«Ноль целых, пять десятых»

Пример 2. Перевести обыкновенную дробь 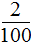в десятичную дробь.

Целая часть отсутствует. Записываем сначала 0 и стáвим запятую:

Теперь смóтрим на количество нулей в знаменателе. Видим, что там два нуля. А в числителе только одна цифра. Чтобы сделать количество цифр и количество нулей одинаковым, добавим в числителе перед цифрой 2 один ноль. Тогда дробь примет вид . Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь:

В полученной десятичной дроби 0,02 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.

Десятичная дробь 0,02 читается так:

«Ноль целых, две сотых».

Пример 3. Перевести обыкновенную дробь 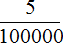в десятичную дробь.

Записываем 0 и стáвим запятую:

Теперь посчитаем количество нулей в знаменателе дроби 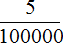. Видим, что там пять нулей, а в числителе только одна цифра. Чтобы сделать количество нулей в знаменателе и количество цифр в числителе одинаковым, нужно в числителе перед цифрой 5 дописать четыре нуля:

Теперь можно продолжить десятичную дробь. Записываем после запятой числитель дроби

В полученной десятичной дроби 0,00005 количество цифр после запятой и количество нулей в знаменателе дроби 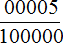одинаково. Значит дробь переведена правильно.

Десятичная дробь 0,00005 читается так:

«Ноль целых, пять стотысячных».

Перевод неправильных дробей в десятичную дробь

Неправильная дробь это дробь, у которой числитель больше знаменателя.

Бывают неправильные дроби, у которых в знаменателе содержатся числа 10, 100, 1000 или 10000. Такие дроби можно переводить в десятичные. Но перед переводом в десятичную дробь, у таких дробей необходимо выделять цéлую часть.

Пример 1. Перевести неправильную дробь 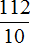в десятичную.

Дробь 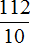является неправильной. Чтобы перевести такую дробь в десятичную, нужно в первую очередь выделить у нее цéлую часть. Вспоминаем, как выделять целую часть у неправильных дробей. Если забыли, советуем вернуться к этой теме и хорошенько изучить её.

Итак, выделим целую часть в неправильной дроби 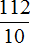. Напомним, что дробь означает деление — в данном случае деление числа 112 на число 10. Деление нужно выполнить с остатком:

Посмóтрим на этот рисунок и соберём новое смешанное число, подобно детскому конструктору. Частное 11 будет целой частью, остаток 2 — числителем дробной части, делитель 10 — знаменателем дробной части:

Мы получили смешанное число 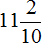. Его и переведём в десятичную дробь. А как переводить такие числа в десятичные дроби мы уже знаем. Сначала записываем целую часть и ставим запятую:

Теперь посчитаем количество нулей в знаменателе дробной части. Видим, что там один ноль. И в числителе дробной части одна цифра. Значит количество нулей в знаменателе дробной части и количество цифр в числителе дробной части одинаково. Это даёт нам возможность сразу записать после запятой числитель дробной части:

Значит, неправильная дробь 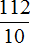при переводе в десятичную обращается в 11,2

Десятичная дробь 11,2 читается так:

«Одиннадцать целых, две десятых».

Пример 2. Перевести неправильную дробь 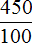в десятичную дробь.

Это неправильная дробь, поскольку числитель больше знаменателя. Но её можно перевести в десятичную дробь, поскольку в знаменателе содержится число 100.

В первую очередь выделим целую часть этой дроби. Для этого разделим уголком 450 на 100:

Соберём новое смешанное число — получим 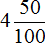. Теперь переведём его в десятичную дробь. Записываем целую часть и ставим запятую:

Теперь посчитаем количество нулей в знаменателе дробной части и количество цифр в числителе дробной части. Видим, что количество нулей в знаменателе и количество цифр в числителе одинаково. Это даёт нам возможность сразу записать числитель дробной части после запятой:

Значит неправильная дробь 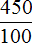при переводе в десятичную обращается в 4,50

При решении задач, если в конце десятичной дроби оказываются нули, их можно отбросить. Давайте и мы отбросим ноль в нашем ответе. Тогда мы получим 4,5

Это одна из интересных особенностей десятичных дробей. Она заключается в том, что нули которые стоят в конце дроби, не придают этой дроби никакого веса. Другими словами, десятичные дроби 4,50 и 4,5 равны и между ними можно поставить знак равенства:

Возникает вопрос «а почему так происходит?» Ведь на вид 4,50 и 4,5 разные дроби. Весь секрет кроется в основном свойстве дроби, котором мы изучали ранее. Мы попробуем доказать, почему равны десятичные дроби 4,50 и 4,5, но после изучения следующей темы, которая называется «перевод десятичной дроби в смешанное число».

Перевод десятичной дроби в смешанное число

Любая десятичная дробь может быть обратно переведена в смешанное число. Для этого достаточно уметь читать десятичные дроби.

Например, переведём 6,3 в смешанное число. 6,3 это шесть целых и три десятых. Записываем сначала шесть целых:

и рядом три десятых:

Пример 2. Перевести десятичную дробь 3,002 в смешанное число

3,002 это три целых и две тысячных. Записываем сначала три целых

и рядом записываем две тысячных:

3

Пример 3. Перевести десятичную дробь 4,50 в смешанное число

4,50 это четыре целых и пятьдесят сотых. Записываем четыре целых

и рядом пятьдесят сотых:

Кстати, давайте вспомним последний пример из предыдущей темы. Мы сказали, что десятичные дроби 4,50 и 4,5 равны. Также мы сказали, что ноль можно отбросить. Докажем, что десятичные 4,50 и 4,5 равны. Для этого переведем обе десятичные дроби в смешанные числа.

После перевода в смешанное число десятичная дробь 4,50 обращается в 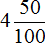, а десятичная дробь 4,5 обращается в

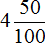
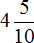
Имеем два смешанных числа и . Переведём эти смешанные числа в неправильные дроби:

Теперь имеем две дроби и . Теперь вспоминаем основное свойство дроби, которое говорит о том, что при умножении (или делении) числителя и знаменателя дроби на одно и то же число, значение дроби не меняется.

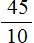
Давайте разделим числитель и знаменатель первой дроби на число 10

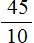
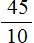
Получили , а это есть вторая дробь. Значит и равны между собой и равны одному и тому же значению:

=

Перевод десятичной дроби в обыкновенную дробь

Любая десятичная дробь может быть обратно переведена в обыкновенную дробь. Для этого опять же достаточно уметь читать десятичные дроби. Например, переведём 0,3 в обыкновенную дробь. 0,3 это ноль целых и три десятых. Записываем сначала ноль целых:

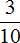
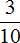
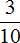
и рядом три десятых 0 . Ноль по традиции не записывают, поэтому окончательный ответ будет не 0, а просто .

Пример 2. Перевести десятичную дробь 0,02 в обыкновенную дробь.

0,02 это ноль целых и две сотых. Ноль не записываем, поэтому сразу записываем две сотых

Пример 3. Перевести 0,00005 в обыкновенную дробь

0,00005 это ноль целых и пять сто тысячных. Ноль не записываем, поэтому сразу записываем пять сто тысячных

Пример 4. Перевести 3,5 в обыкновенную дробь

Сначала переведём данную десятичную дробь в смешанное число:

Теперь смешанное число 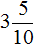переведём в неправильную (обыкновенную) дробь:

Пример 5. Перевести 1,25 в обыкновенную дробь

Сначала переведём данную десятичную дробь в смешанное число:

Теперь смешанное число переведём в неправильную (обыкновенную) дробь:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

37 thoughts on “Десятичные дроби”

все круто, понятно и доступно.
спасибо. долгий путь до высшей математики предстоит)

Спасибо за сайт! Всё очень понятно. Не понимал что такое дробь уже с пятого класса (щя 2 курс колледжа), прочитав на сайте всё понял, спасибо вам.

Огромное спаасибо! Просто, интересно, и очень нужно! Успехов и радости в жизни!

Я не понимаю как перевести обыкновенные дробь в десятичную с некруглым знаменателем

А что значит десятичная дробь с некруглым знаменателем? У десятичной дроби всегда круглый знаменатель — 10, 100, 1000. Чтобы перевести некруглый знаменатель в десятичный, нужно найти НОК с этим круглым числом. И множить…

Источник