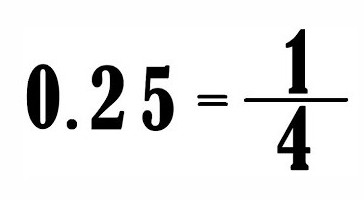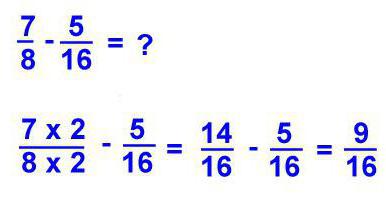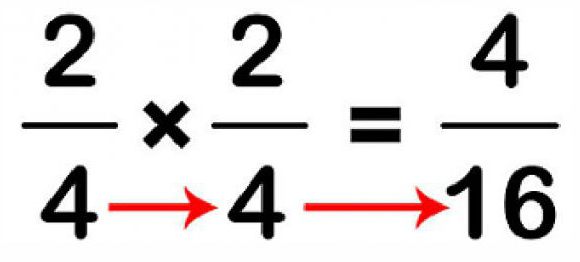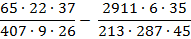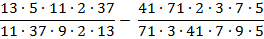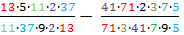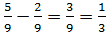Для чего нужны дроби
Изучая царицу всех наук – математику, в определенный момент все сталкиваются с дробями. Хотя это понятие (как и сами виды дробей или математические действия с ними) совсем несложное, к нему нужно относиться внимательно, ведь в реальной жизни за пределами школы оно очень пригодится. Итак, давайте освежим свои знания о дробях: что это, для чего нужно, какие виды их бывают и как совершать с ними различные арифметические действия.
Ее величество дробь: это что такое
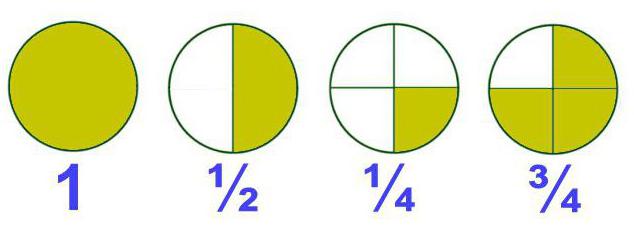
Дробями в математике называются числа, каждое из которых состоит из одной или более частей единицы. Такие дроби еще называют обыкновенными, либо простыми. Как правило, они записываются в виде двух чисел, которые разделены горизонтальной или слеш-чертой, она называется «дробной». Например: ½, ¾.
Верхнее, или первое из этих чисел – это числитель (показывает, сколько взято долей от числа), а нижнее, или второе – знаменатель (демонстрирует, на столько частей разделена единица).
Дробная черта фактически выполняет функции знака деления. К примеру, 7:9=7/9
Традиционно обыкновенные дроби меньше единицы. В то время как десятичные могут быть больше ее.
Для чего нужны дроби? Да для всего, ведь в реальном мире далеко не все числа целые. К примеру, две школьницы в столовой купили в складчину одну вкусную шоколадку. Когда они уже собрались делить десерт, встретили подружку и решили угостить и и ее. Однако теперь необходимо правильно разделить шоколадку, если учесть, что она состоит из 12 квадратиков.
Поначалу девчонки хотели разделить все поровну, и тогда каждой бы досталось по четыре кусочка. Но, раздумав, они решили угостить подружку, не 1/3, а 1/4 шоколадки. А поскольку школьницы плохо изучали дроби, то они не учли, что при подобном раскладе в результате у них останется 9 кусочков, которые очень плохо делятся на двоих. Этот довольно простой пример показывает, насколько важно уметь правильно находить часть от числа. А ведь в жизни подобных случаев гораздо больше.
Виды дробей: обыкновенные и десятичные
Все математические дроби делятся на два больших разряда: обыкновенные и десятичные. Об особенностях первого из них было рассказано в предыдущем пункте, так что теперь стоит уделить внимание второму.
Десятичной называют позиционную запись дроби числа, которая фиксируется на письме через запятую, без черточки или слеша. Например: 0,75, 0,5.
Фактически десятичная дробь идентична обыкновенной, однако, в ее знаменателе всегда единица с последующими нулями – отсюда произошло и ее название.
Подвиды обыкновенных дробей
Есть такие виды дробей простых.
Подвиды десятичной дроби
В отличие от простой, десятичная дробь делится всего на 2 вида.
Сложение дробей
Проводить различные арифметические манипуляции с дробями немного сложнее, чем с обычными числами. Однако, если усвоить основные правила, решить любой пример с ними не составит особого труда.
Итак, чтобы сложить между собою дроби, прежде всего, нужно сделать так, чтобы у обоих слагаемых были одинаковые знаменатели. Для этого предстоит найти наименьшее число, которое способно поделиться без остатка на знаменатели слагаемых чисел.
Например: 2/3+3/4. Наименьшим общим кратным для них будет 12, следовательно, необходимо, чтобы в каждом знаменателе стояло это число. Для этого числитель и знаменатель первой дроби умножаем на 4, получается 8/12, аналогично поступаем со вторым слагаемым, но только множим на 3 – 9/12. Теперь можно легко решить пример: 8/12+9/12= 17/12. Получившаяся дробь – это неправильная величина, поскольку числитель больше знаменателя. Ее можно и нужно пребразовать в правильную смешанную, разделив 17:12= 1 и 5/12.
В случае, если слагаются смешанные дроби, сначала действия совершаются с целыми числами, а потом с дробными.
Если слагать 2 десятичные дроби, важно, чтобы после запятой было одинаковое количество цифр. Если это не так, нужно просто дописать необходимое количество нулей, ведь в десятичной дроби это можно сделать безболезненно. Например, 3,5+3,005. Чтобы решить это задание, нужно к первому числу прибавить 2 ноля и далее поочередно слагать: 3,500+3,005=3,505.
Вычитание дробей
Вычитая дроби, стоит поступать так же, как и при сложении: свести к общему знаменателю, отнять один числитель от другого, при необходимости перевести результат в смешанную дробь.
Например: 16/20-5/10. Общим знаменателем будет 20. Нужно привести вторую дробь к этому знаменателю, умножив обе ее части на 2, получается 10/20. Теперь можно решать пример: 16/20-10/20= 6/20. Однако этот результат относится к сократимым дробям, поэтому стоит поделить обе части на 2 и получается результат – 3/10.
Умножение дробей
Деление и умножение дробей – значительно более простые действия, нежели сложение и вычитание. Дело в том, что, выполняя эти задания, нет необходимости искать общий знаменатель.
Чтобы умножить дроби, нужно просто поочередно перемножить между собою оба числителя, а затем и оба знаменателя. Получившийся результат сократить, если дробь – это сократимая величина.
Например: 4/9х5/8. После поочередного умножения получается такой результат 4х5/9х8=20/72. Такая дробь сократима на 4, поэтому конечный ответ в примере – 5/18.
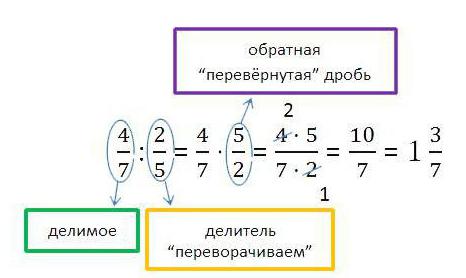
Как делить дроби
Например, деление дробей 5/19 и 5/7. Чтобы решить пример, нужно поменять местами знаменатель и числитель второй дроби и умножить: 5/19х7/5=35/95. Результат можно сократить на 5 – получается 7/19.
В случае, если необходимо разделить дробь на простое число, методика немного отличается. Изначально стоит записать это число как неправильную дробь, а потом делить по той же схеме. Например, 2/13:5 нужно записать как 2/13: 5/1. Теперь нужно перевернуть 5/1 и умножить получившиеся дроби: 2/13х1/5= 2/65.
Иногда приходится совершать деление дробей смешанных. С ними нужно поступать, как и с целыми числами: превратить в неправильные дроби, перевернуть делитель и умножить все. Например, 8 ½ : 3. Превращаем все в неправильные дроби: 17/2: 3/1. Далее следует переворот 3/1 и умножение: 17/2х1/3= 17/6. Теперь следует перевести неправильную дробь в правильную – 2 целых и 5/6.
Итак, разобравшись с тем, что такое дроби и как можно с ними совершать различные арифметические действия, нужно постараться не забывать об этом. Ведь люди всегда более склонны делить что-то на части, нежели прибавлять, поэтому нужно уметь делать это правильно.
Проект «Зачем нужны дроби»
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Департамент по образованию, культуре, молодежи и спорту администрации г. Ишима
Муниципальное автономное дошкольное образовательное учреждение
«Центр развития ребенка детский сад № 24» города Ишима
Детская исследовательская работа по познавательному развитию
«Что такое дроби и для чего они нужны в жизни человека?»
В рамках конкурса «Я-исследователь»
Выполнил: Щербакова Лиза
МА ДОУ ЦРР д/с №24 г.Ишима
Руководитель: Бохан И.Ю.
воспитатель первой категории
МА ДОУ ЦРР д/с №24 г.Ишима
Сведения об авторе:
Щербаква Лиза, 6 лет, воспитанник подготовительной к школе группы №7 МА ДОУ ЦРР д/с №24 г. Ишима.
Участница конкурсов различного уровня:
Международный конкурс ЧИП для детей и воспитателей, 3 место.
Конкурс детского творчества «Цветочный калейдоскоп», 2 место.
Городской конкурс «Красная книга глазами детей».
Конкурс рисунков «Мы – наследники победы».
Городской конкурс «Мир роботов», номинация рисунок, 3 место
Спартакиада дошкольных учреждений г. Ишима, 1 место.
Малышами мы не осознавали, что когда брали дольку апельсина, что это уже часть от целого.
Цель работы: Выяснить роль дробей в жизни людей.
1. Узнать? что такое дроби.
2. Узнать, откуда появились дроби.
3. Узнать, нужны ли дроби в жизни человека.
Гипотеза: Дроби очень важны в жизни человека. С помощью дробей выполняют математические расчеты.
Методы исследования: наблюдение, работа с литературой, поиск информации в сети интернет.
Содержание творческого проекта.
Здравствуйте, меня зовут Лиза, мне 6 лет. Как и любому ребенку, мне интересно поиграть и повеселиться, но больше всего я люблю узнавать что-то новое, интересное о том, что меня окружает.
Однажды в детском саду, воспитатель, Инна Юрьевна, учила нас делить круг на равные части, называть эти части 1/8, 2/8, 3/8 и.т. И рассказала нам, что эти части называются дробями.
И мне очень стало интересно, что такое дроби, откуда они взялись и зачем нужны в жизни человека?
Откуда появились дроби?
Придя домой, из детского сада, я попросила маму помочь мне разобраться, откуда появились дроби и для чего они нужны.
Вместе мы из статей в интернете узнали, что дроби появились еще в древности, когда у людей появилась необходимость измерять длину, площадь, время, вести расчеты за купленные или проданные товары. Не всегда удавалось измерение выразить целым числом.
Приходилось учитывать части и доли. Так появились дроби.
В русском языке слово дробь появилось в VIII веке, оно происходит от глагола «дробить» — разбивать, ломать на части. В первых учебниках математики (в VII веке) дроби так и назывались — «ломаные числа». У других народов название дроби также связано с глаголами «ломать», «разбивать», «раздроблять».
Для чего нужны дроби?
Изучая книги и статьи в интернете, я узнала что дроби нужны для решения математических задач и используются в различных профессиях, например:
в медицине, при изготовлении лекарств, чтобы приготовить необходимое лекарство нужно знать его состав, записанный с помощью дробей, или когда врач назначает больному ½ таблетки
в кулинарии при изготовлении бисквита необходимо взять 3 яйца, растереть с 1 1/3 сахара и смешать с 1 1/3 стакана муки и т.д.
в парикмахерской при завивке волос, для приготовления раствора для покраски волос и для завивки.
и других профессиях.
А так же мне стало очень интересно, где мы можем использовать дроби дома и в детском саду. И мы стали наблюдать.
Использование дробей в повседневной жизни.
Дома, мы с сестрой решили слепить блинчики из пластилина. Блины удались, но нам показалось, что если разделить каждый блин на части и соединить между собой, то получатся необычные блинчики.
Наше творчество привлекло и брата. Теперь нам предстояло снова слепить блины одного цвета и каждый разделить уже на три части. Всем досталось по 1/3 блина.
Мы делили два блина на троих-вот это да.
Какое природное явление удивительно красиво? Радуга!
В группе мы изготовили панно «Радуга» из 7 полосок разного цвета, но одинакового размера. Оказалось, что полоска красного цвета, моего любимого, это 1/7 часть от всей радуги.
А так же у нас есть очень любимое панно «Год», которое мы изготовили в виде квадрата и разделили на 4 равные части (времена года).
Из всего этого можно сделать вывод, что дроби необходимы для деления предметов на равные части.
Изготовление дидактической игры «Необычные круги».
Узнав, что такое дроби и для чего они необходимы, я захотела поделиться со своими друзьями в группе. А что бы интересней рассказать, решили изготовить игру «Необычные круги». Для этого вырезали из цветного картона круги и разрезали их на части. Что бы узнать, как называется часть и дробь, необходимо собрать круги из частей соответствующего цвета.
Эта игра так же пополнит наш математический уголок в группе.
Наше предположение: дроби очень важны в жизни человека, с помощью дробей выполняют математические расчеты, подтвердилось. Мы так же узнали, что дроби используются в различных профессиях и в повседневной жизни для деления на части.
Но, что было бы, если бы вообще не было дробей?
Можно, предположить, что люди бы ссорились, ругались из – за неравных частей при делении на части, у поворов получались бы не вкусные блюда, пересоленые, тесто бы не получалось, у медиков лекарства были бы бесполезны или вредны и т.д. Значит дроби очень важны!
Перспектива разработки темы.
Мне очень понравилось проводить исследование по данной теме, изучать книги, статьи в интернете. Я почувствовала себя настоящим ученым, исследователем. Я очень рада, что могу рассказать своим друзьям о том, что я узнала. А так же наш уголок математики пополнится новой игрой.
Практическая значимость моей работы заключается:
• в рассказе своим друзьям о дробях, ознакомлении с полученной информацией, в наблюдении за предметами.
• в изготовлении дидактической игры «Необычные круги»
М.Я.Выгодский “Арифметика и алгебра в Древнем мире”(М. Наука,1967г)
2 Г.И.Глейзер “История математики в школе”(М. Просвещение,1964г)
3 И.Я.Депман “История арифметики” (М. Просвящение, 1959г)
4 Н.Я.Виленкин «За страницами учебника математики. Арифметика» (М. Просвещение, 2008)
Творческие проекты и работы учащихся
В данном исследовательском проекте по математике на тему «Обыкновенные дроби в жизни людей» автор изучает историю возникновения дробей, даёт определение «обыкновенная дробь», а также наглядно показывает обыкновенные дроби.
Подробнее о проекте:
Автор творческого проекта по математике на тему «Обыкновенные дроби в жизни людей» изучил использование обыкновенных дробей в профессиональной деятельности человека, а также порассуждал и аргументированно доказал важность знания и применения дробей для профессии «Разметчик». Также в работе можно найти определение других математических дробей.
Оглавление
Введение
1. Теоретическая часть.
1.1 Понятие дроби.
1.2 История возникновения дробей.
1.3 Использование обыкновенных дробей в профессиональной деятельности человек.
1.3.1 Дроби для профессии «Разметчик».
2. Практическая часть.
2.1. Мои наблюдения.
Заключение
Список использованной литературы
Введение
С первого знакомства с дробями было понятно, что они очень необычные числа, начиная с их непривычной записи и заканчивая сложными правилами действий с ними.
В обычной жизни, и взрослым, и детям каждый день приходится сталкиваться с проблемой деления целого на части, и даже в определенный момент кажется, что нас больше окружают не целые, а дробные числа, что является актуальностью данной темы.
Мне стало интересно узнать: как и когда появились дроби? В какой сфере жизни больше всего практически их применяют? Хотелось в ходе исследования этого вопроса убедиться и убедить других в необходимости дробей в повседневной жизни.
Объект исследования: обыкновенные дроби
Предмет исследования: использование дробей в нашей повседневной жизни.
Цель: показать, что дроби нужны не только в математике, но и в повседневной жизни.
Понятие дроби
В математике применяются следующие виды дробей:
Дроби разные нужны, дроби всякие важны
Десятичная дробь, это дробь, которая записывается без знаменателя.
Выглядят они так: 5,6; 3,17; 0,17 и т.д. На самом деле это особая запись обыкновенных дробей, у которых знаменатель равен 10, 100, 1000 и т. д.
История возникновения дробей
Можно предположить, что потребность делить целое на части возникала ещё в первобытном обществе. Могло быть и так…
Дроби в Древнем Египте
У них числитель всегда единица. Лишь значительно позже у греков, затем у индийцев и других народов стали входить в употребление и дроби общего вида, называемые обыкновенными, у которых числитель и знаменатель могут быть любыми натуральными числами. В Древнем Египте архитектура достигла высокого развития. Чтобы строить грандиозные пирамиды и храмы, чтобы вычислять длины, площади и объемы фигур, необходимо было знать арифметику.
Из расшифрованных сведений на папирусах ученые узнали, что египтяне 4000 лет назад имели десятичную систему счисления, умели решать многие задачи, связанные с потребностями строительства, торговли и военного дела.
Одним из первых известных упоминаний о дробях является математический папирус Ринда. Три более древних текста, в которых упоминаются дроби — это Египетский математический кожаный свиток, Московский математический папирус и Деревянная табличка Ахмима. Папирус Ринда включает таблицу египетских дробей для рациональных чисел вида 1/n, а также 84 математических задачи, их решения и ответы, записанные в виде египетских дробей.
Египтяне ставили иероглиф (ер, «один из» или ре, рот) над числом для обозначения единичной дроби в обычной записи, а в священных текстах использовали линию. У них также были специальные символы для дробей 1/2, 2/3 и 3/4, которыми можно было записывать также другие дроби.
Остальные дроби они записывали в виде суммы долей. Дробь 7/8 они записывали в виде ½ ¼ 1/8, но знак «+» не указывали. А сумму 4+1/3 записывали в виде 41/3. Такая запись смешанных чисел (без знака «+») сохранилась до сих пор.
Вавилонские дроби
Исследователи по-разному объясняют появление у вавилонян шестидесятеричной системы. Число 60 прекрасно делится на 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60, что значительно облегчает всякие расчеты. Шестидесятые доли были привычны в жизни вавилонян.
Вот почему они пользовались шестидесятеричными дробями, имеющими знаменателем всегда число 60 или его степени: 602, 603 и т.д. В этом отношении шестидесятеричные дроби можно сравнить с нашими десятичными дробями.
Вавилонская математика оказала влияние на греческую математику. Следы вавилонской шестидесятеричной системы счисления удержались в современной науке при измерении времени и углов. До наших дней сохранилось деление часа на 60 мин., минуты на 60 с, окружности на 360˚, градуса на 60 мин., минуты на 60с.
Вавилоняне внесли ценный вклад в развитие астрономии. Шестидесятеричными дробями пользовались в астрономии ученые всех народов до XVII века, называя их астрономическимидробями. В отличие от них, дроби общего вида, которыми пользуемся мы, были названы обыкновенными.
Дроби в Древней Греции
Греки работали с обыкновенными дробями не часто, поэтому использовали различные обозначения. Герон и Диофант, самые известные арифметики среди древнегреческих математиков, записывали дроби в алфавитной форме, причем числитель располагали под знаменателем. Но в принципе предпочтение отдавалось либо дробям с единичным числителем, либо шестидесятеричным дробям.
Недостатки греческой системы счисления относят к их любви к строгости, которое заметно увеличило трудности, связанные с анализом отношения несоизмеримых величин. Слово «число» греки понимали, как набор единиц, поэтому то, что мы теперь рассматриваем как единое число – дробь, – греки понимали, как отношение двух целых чисел. Именно этим объясняется, почему обыкновенные дроби редко встречались в греческой арифметике.
Дроби в Древнем Китае
В Древнем Китае уже пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи: цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. Так записывались дроби на протяжении двух веков, а в V веке китайский ученый Цзу-Чун-Чжи принял за единицу не чи, а чжан = 10 чи, тогда эта дробь выглядела так: 2 чжана, 1 чи, 3 цуня, 5 долей, 4 порядковых, 3 шерстинки, 6 тончайших, 0 паутинок.
Дроби на Руси
В русском языке слово «дробь» появилось лишь в VIII веке. Происходит оно от слова «дробить, разбивать, ломать на части». В русских рукописных арифметиках XVII в. дроби называли долями, позднее «ломаными числами». В старых руководствах существуют следующие названия дробей на Руси:
Славянская нумерация употреблялась в России до XVI века, затем в страну начала постепенно проникать десятичная система счисления. Она окончательно вытеснила славянскую нумерацию при Петре I.
Дроби в других государствах древности
В китайской «Математике в девяти разделах» уже имеют место сокращения дробей и все действия с дробями. У индийского математика Брахмагупты найдена достаточно развитую систему дробей. У него встречаются разные дроби: и основные, и производные с любым числителем. Числитель и знаменатель записываются так же, как и у нас сейчас, но без горизонтальной черты, а просто размещаются один над другим.
Арабы первыми начали отделять чертой числитель от знаменателя.
Леонардо Пизанский уже записывает дроби, помещая в случае смешанного числа, целое число справа, но читает так, как принято у нас. В XV – XVI столетиях учение о дробях приобретает уже знакомый нам теперь вид и оформляется приблизительно в те самые разделы, которые встречаются в наших учебниках.
Следует отметить, что раздел арифметики о дробях долгое время был одним из наиболее трудных. Недаром у немцев сохранилась поговорка: «Попасть в дроби», что означало – зайти в безвыходное положение. Считалось, что тот, кто не знает дробей, не знает и арифметики.
Использование обыкновенных дробей в профессиональной деятельности человека
В медицине. Чтобы приготовить необходимое лекарство нужно знать его состав, записанный с помощью дробей, или, когда врач назначает больному ½ таблетки.
Дроби в кулинарии. Поварам нужны дроби для соблюдения пропорции при приготовлении блюда. В рецептах очень часто используются такие фразы, например, как одна вторая стакана, четверть столовой ложки.
Дроби в музыке. Учащиеся музыкальной школы знакомятся с дробями раньше, чем в общеобразовательной школе. С первых дней занятий дети знакомятся с такими понятиями как размер и длительности нот. Древнегреческий философ Пифагор (570 г. до н. э.), один из самых первых установил связь музыки и математики. Он создал учение о звуке. Пифагор связал длительность звучания нот с дробями.
Счёт длительностей в музыке ведётся от целой ноты, которая считается до четырёх. В целой ноте 2 половинные, 4 четверти, 8 восьмых, 16 шестнадцатых. Так музыка живёт в согласии с математикой.
Дроби в географии: Материк Евразия занимает 1/3 часть суши;
Масштаб карты равен 1/50000
Участки земной поверхности изображаются на карте в уменьшенном виде, для этого используется понятие масштаба: отношение длины отрезка на карте к длине соответствующего отрезка на местности.
Например, масштаб карты 1/10000 означает, что 1см на карте соответствует 10000 см на местности.
Дроби в спорте. Когда смотрим ½ финала матча по футболу.
Дроби в пропорции человека тоже связаны с дробями. Голова маленького ребенка составляет 1/5 часть роста человека. Голова подростка – 1/6. А голова взрослого человека – 1/8 часть роста. Основываясь на этих данных, была создана кукла «Барби».
В настоящее время невозможно представить ни одну отрасль промышленности или сельского хозяйства, или строительства, где бы в расчётах не встречалось дробных чисел.
Дроби для профессии «Разметчик»
Разметчику приходится решать интересные и подчас нелегкие геометрические задачи, производить арифметические расчеты и т. д.
Возможно ли деление данных пластинок на более крупные доли? Разметчик подумал, произвел какие-то арифметические расчеты с дробями и нашел все-таки самый экономный способ деления данных пластинок.
Впоследствии он легко дробил 5 пластинок для распределения их равными долями между шестью деталями, 13 пластинок для 12 деталей, 13 пластинок для 36 деталей, 26 для 21 и т.п.
Оказывается, разметчик представил дробь 7\12 в виде суммы единичных дробей 1\3 + 1\4. Значит, если из 7 данных пластинок 4 разрезать на три равные части каждую, то получим 12 третей, то есть по одной трети для каждой детали. Остальные 3 пластинки разрежем 4 равные части каждую, получим 12 четвертей, то есть по одной четверти для каждой детали. Аналогично, используя представления дробей в виде суммы единичных дробей 5\6 = 1\2+1\3; 13\12 =1\3+3\4; 13\36 =1\4+1\9.
Практическая часть. Мои наблюдения
Ситуация 1. В парке стоит молодой человек с букетом цветов:
Дроби в кулинарии. «Пряники». Видеоролик. (Приложение 2)
Поварам нужны дроби для соблюдения пропорции при приготовлении блюда. В рецептах очень часто используются такие фразы, например, как одна вторая стакана, четверть столовой ложки.
Ситуация 2. Ученик в одежде повара. Готовит тесто для пряников.
— Для пряников понадобится 1 яйцо, один с четвертью стакана муки, две с половиною столовой ложки меда, треть чайной ложки соли, половина чайной ложки имбиря. Всё тщательно перемешиваем и печем пряники.
Дроби в кулинарии. «Пирожное». Видеоролик (Приложение 3)
Приготовленные блюда нужно умело делить на порции.
Ситуация 3. На столе стоит тарелка. В ней 5 пирожное.
— На день рождения пришли 6 друзей. Передо мной встал вопрос: «Как поровну разделить 5 пирожное между 6 человек»?
Решение было такое: нужно 5 пирожное разделить пополам каждый. Затем ещё 2 пирожное разделить на 3 части. Получается 6 абсолютно равных частей.
Дроби в математике.
Учитель математики после изучения сокращения дробей задал домашнее задание. Найти значение выражения рациональным способом.
На первый взгляд, обыкновенные натуральные числа. Сначала надо решить действия в скобках, потом делить и умножать. Но, здесь должна быть какая-то хитрость?! Надо найти рациональный способ. Я решил данное выражение так:
1) Записал выражение в виде дроби.
2) Преобразовал каждое натуральное число в виде произведения двух множителей.
3) В полученных дробях получились числа, которых можно сократить.
Заключение
При выполнении своего проекта, я узнал много нового и интересного о дробях. Думаю, что эти знания пригодятся в учебе. Прочитал много книг и разделов из энциклопедий. Познакомился с первыми дробями, которыми оперировали люди, узнал новые для меня имена ученых, внесших свой вклад в развитие учения о дробях. А особенно то, что дроби используются почти во всех сферах деятельности человека, а это значит, что людям всех профессий нужно обязательно изучать дроби! Уметь решать задачи на дроби, знать правила сложения и вычитания, умножения и деления дробей.
Без знания математики, особенно знания дробей вся современная жизнь была бы невозможна. Например, у нас не было бы хороших домов, потому что строители должны уметь измерять, считать, сооружать. Наша одежда была бы очень грубой, так как ее нужно хорошо скроить, то есть точно все измерить, Не было бы ни какой большой промышленности, ни какой коммерции.
И конечно, не было бы радио, телевидения, кино, телефона и тысяч других вещей, составляющих часть нашей цивилизации. Использование дробей, измерения «на сколько?», «как долго?» являются жизненно необходимой частью мира, в котором мы живем.
В заключении можно сказать, что дроби бывают разные, дроби бывают важные. Знание понятия математическая дробь очень важно!
Считаю, что материалы моей работы будут интересными для других учащихся. Они могут быть использованы как на уроке, так и для проведения учителями внеклассных мероприятий по математике.