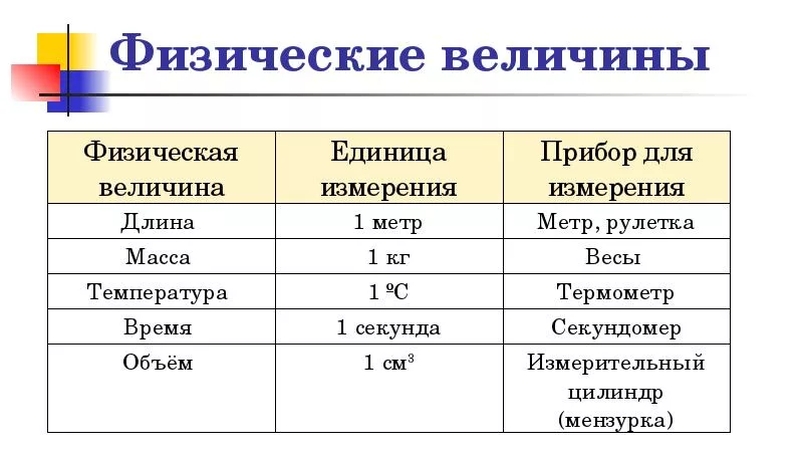
Для чего нужны физические величины

Физическая величина

Физи́ческая величина́ — физическое свойство материального объекта, физического явления, процесса, которое может быть охарактеризовано количественно.

Значение физической величины — одно или несколько (в случае тензорной физической величины) чисел, характеризующих эту физическую величину, с указанием единицы измерения, на основе которой они были получены.

Размер физической величины — значения чисел, фигурирующих в значении физической величины.

Например, автомобиль может быть охарактеризован с помощью такой физической величины, как масса. При этом, значением этой физической величины будет, например, 1 тонна, а размером — число 1, или же значением будет 1000 килограмм, а размером — число 1000. Этот же автомобиль может быть охарактеризован с помощью другой физической величины — скорости. При этом, значением этой физической величины будет, например, вектор определённого направления 100 км/ч, а размером — число 100.

Размерность физической величины — единица измерения, фигурирующая в значении физической величины. Как правило, у физической величины много различных размерностей: например, у длины — нанометр, миллиметр, сантиметр, метр, километр, миля, дюйм, парсек, световой год и т. д. Часть таких единиц измерения (без учёта своих десятичных множителей) могут входить в различные системы физических единиц — СИ, СГС и др.

Часто физическая величина может быть выражена через другие, более основополагающие физические величины. (Например, сила может быть выражена через массу тела и его ускорение). А значит, соответственно, и размерность такой физической величины может быть выражена через размерности этих более общих величин. (Размерность силы может быть выражена через размерности массы и ускорения). (Часто такое представление размерности некоторой физической величины через размерности других физических величин является самостоятельной задачей, которая в некоторых случаях имеет свой смысл и назначение.) Размерности таких более общих величин часто уже являются основными единицами той или другой системы физических единиц, то есть такими, которые сами уже не выражаются через другие, ещё более общие величины.

Пример.
Если физическая величина мощность записывается как

P = 42,3 × 10³ Вт = 42,3 кВт,

Р — это общепринятое литерное обозначение этой физической величины, 42,3 × 10³ Вт — значение этой физической величины, 42,3 × 10³ — размер этой физической величины.

Вт — это сокращённое обозначение одной из единиц измерения этой физической величины (ватт). Литера к является обозначением десятичного множителя «кило» Международной системы единиц (СИ).

Содержание

Размерные и безразмерные физические величины

Аддитивные и неаддитивные физические величины

Экстенсивные и интенсивные физические величины

Некоторые физические величины, такие как момент импульса, площадь, сила, длина, время, не относятся ни к экстенсивным, ни к интенсивным.

От некоторых экстенсивных величин образуются производные величины:

Скалярные, векторные, тензорные величины

Система единиц физических величин

Система единиц физических величин — совокупность единиц измерений физических величин, в которой существует некоторое число так называемых основных единиц измерений, а остальные единицы измерения могут быть выражены через эти основные единицы. Примеры систем физических единиц — Международная система единиц (СИ), СГС.

Символы физических величин

В качестве символов физических величин обычно выступают отдельные прописные и строчные литеры латинского или греческого алфавита. Часто к обозначениям добавляют верхние или нижние индексы, обозначающие, к чему относится величина, например E_п часто обозначает потенциальную энергию, а c_p — теплоёмкость при постоянном давлении.

Источник

Физические величины. Измерение физических величин. Точность и погрешность измерений

Цели урока:

1) Обучающая: обеспечить формирование у учащихся представлений о физической величине, обеспечит усвоение учащимися теоретических знаний об основных характеристиках физической величины, познакомить учащихся с простейшими измерительными приборами, научить определять цену деления и точность отсчета при использовании различных шкал.

2) Развивающая: способствовать расширению кругозора учащихся о физике; умение находить некоторые закономерности; развитие памяти, самостоятельного суждения.

3) Воспитывающая: интерес, любознательность, наблюдательность, аккуратность в записях.

Ход урока:

1. Организационный этап.

Здравствуйте. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.

2. Актуализация знаний

Прежде чем начинать наш с вами уже второй урок в курсе Физики, хотелось бы вспомнить то, о чем мы говорили на предыдущем занятии.

Мы ввели понятие «Физическое тело». Что же это? Это любой предмет, окружающего нас мира.

Физическое явление — все изменения, которые происходят с физическими полями и телами.

Для описания физических тел и физических явлений используют физические величины.

Например, для описания деревянного бруска нам необходимо использовать такие физические величины как масса, длина, ширина, высота, объем.

Откройте тетради и запишите число и тему нашего урока.

3. Этап получения новых знаний.

Для описания физических тел и физических явлений используют физические величины.

Например, для описания деревянного бруска нам необходимо использовать такие физические величины как масса, длина, ширина, высота, объем.

То есть физическая величина это то, что мы можем измерить. Измеряемое свойство тела или явления.

Каждая физическая величина имеет название, например масса; Буквенное обозначение (массу обозначают латинской буквой эм), способ измерения (с помощью весов), числовое значение (например, масса человека равна 45), и единицы измерения (кг). Получаем, масса тела равна 45 кг.

Для каждой физической величины приняты свои единицы измерения. Для удобства все страны мира стремятся пользоваться одинаковыми единицами измерения физических величин. С 1963 года во многих странах мира используется Международная система единиц — СИ (система интернациональная). В этой системе основной единицей длины является метр, времени — секунда, массы — килограмм.

Существует единицы, которые в 10, 100, 1000 раз больше принятых. Такие единицы называет кратными, и именуются с соответствующими греческими приставками. Например, десяти соответствует приставка «дека», стам — «гекто», тысячи — «кило».

Если используют единицы, которые в 10, 100, 1000 раз меньше принятых единиц (это дольные единицы), то используют приставки, взятые из латинского языка. «Деци» — ноль целых одна десятая, «санти» — ноль целых одна сотая, «милли» — ноль целых одна тысячная.

Измерения очень важны в нашей жизни, для их проведения необходимы измерительные приборы. Самые простые приборы для измерения длины линейка, рулетка, мерная лента.

Для измерения объема жидкости мензурка, мерный цилиндр, мерная колба.

Для измерения температуры используют комнатный, водный, медицинский термометры. Медицинский, в свою очередь, бывает электронный и ртутный.

Существуют и другие измерительные приборы. Например, времени секундомер, часы. Силы — динамометр. Давления, атмосферного — барометр, газов в сосуде — манометр.

Приборы делят на шкальные и цифровые. Каждый шкальный прибор имеет шкалу и цену деления.

Шкала измерительного прибора называют совокупность отметок и цифр на отсчетном устройстве прибора, соответствующая ряду последовательных значений измеряемой величины

Цена деления — значение наименьшего деления шкалы прибора.

Для определения цены деления шкалы нужно от большего числа, соответствующего какому — либо делению шкалы, вычесть меньшее и полученную разность поделить на число делений между цифрами. Получаем 0,1 сантиметра на деление.

Какой же прибор точнее, цена деления которого меньше или больше?

Рассмотрим мерную ленту А) и линейку б). У обоих приборов единицы измерения совпадают!

Для нахождения цены деления мерной ленты возьмем два рядом стоящих значения на шкале, от большего вычтем меньшее и разделим на количество делений между данными цифрами. Получим, 1 сантиметр на деление.

Также определим цену деления для линейки. Количество делений в данном случае 10. Получим, ноль целых одна десятая сантиметра на деление.

Точнее тот прибор у которого цена деления меньше. Значит данная линейка точнее мерной ленты.

То есть, имея меньшую цену деления, мы меньше ошиблись.

Чему же равна погрешность измерительных приборов?

Погрешность равна половине цены деления.

Например, погрешность при измерении температуры равна половине цены деления данного термометра.

Найдем ее: для этого определим цену деления термометра.

Берем два любых значения, например 20 и 10, от большего вычтем меньшее значение и разделим на количество делений между ними, их пять. Получили, что она равна 2 градуса на деление.

Значит погрешность равна 1 градус.

Как же это записать?

T = 20±1 C, где 20 — показания термометра, 1 — погрешность, знак полюс минус использует потому, что ошибиться можно как в большую так и в меньшую сторону.

При записи величин с учетом погрешности следует пользоваться формулой, где

А — измеряемая величина,

а — результат измерений,

Так что же значит измерить физическую величину?

Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу.

Например, чтобы измерить длину отрезка прямой между точками, А и В, надо приложить линейку и по шкале определить сколько сантиметров укладывается между данными точками.

Если физическая величина измеряется непосредственно путем снятия данных со шкалы прибора, то такое измерение называют прямыми. Например, измерение длины бруска, ширины или высоты бруска.

А как же определить объем этого самого бруска. Конечно же, используя формулу. Объем есть произведение длины, ширины и высоты.

В этом случае, когда физическую величину (объем), определили по формуле, говорят, что измерения провели косвенно.

3. Этап обобщения и закрепления нового материала.

Итак, сделаем основные выводы:

— Физическая величина — измеряемое свойство тела или явления

— Каждый шкальный прибор имеет шкалу и цену деления

— Шкала измерительного прибора — это совокупность отметок и цифр на отсчетном устройстве прибора, соответствующая ряду последовательных значений измеряемой величины

— Цена деления (С) — значение наименьшего деления шкалы прибора

— Для определения цены деления шкалы нужно от большего числа, соответствующего какому- либо делению шкалы, вычесть меньшее и, разность поделить на число делений между цифрами

— Погрешность измерительных приборов равна половине цены деления

Для закрепления, изученного материала, ответим на ряд вопросов.

Что такое физическая величина? Какие основные физические величины входят в систему СИ? Какие шкальные измерительные приборы вам известны? Какие цифровые измерительные приборы вам известны? Перечислите приборы для измерения длины, времени, температуры. Что такое цена деления? Как определить цену деления прибора? От чего зависит точность измерения? Что необходимо учитывать при выборе измерительного прибора? Чем отличаются кратные и дольные единицы? Что значит измерить косвенно или прямым способом?

4. Рефлексия.

Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.

5. Домашнее задание: § 4- 5.

1. Из перечисленных приборов выбрать а) шкальные, б) цифровые.

Линейка, весы электронные, напольные (не электронные весы), секундомер, часы наручные механические, часы электронные настенные, динамометр, мензурка, мерный стаканчик, барометр, манометр.

2. Определить цену деления данного прибора.

3. Определить цену деления данного термометра.

4. Определить цену деления и погрешность данной линейки.

5. Какая из данных мерных лент более точная? Почему? Чем точнее можно измерить длину стола линейкой или мерной лентой? Почему?

Источник

Физическая величина — что это такое, и в чем ее измеряют?

Физика — наука, осуществляющая наблюдения за самыми различными предметами и явлениями. А главная ценность этих наблюдений заключается в том, что их можно описать — и выявить причины, закономерности, возможные следствия.

Для того, чтобы дать понятное описание явлению или предмету, необходимо измерить его сразу по нескольким параметрам. Результаты этих измерений и называются физической величиной.

Определение понятия и его практическая суть

Физическая величина — это характеристика, которая с точки зрения своего качества едина для многих объектов, но в количественно верна только для одного из них. К сожалению, это официальное объяснение звучит не слишком понятно, и после него все еще остаются вопросы.

Простыми словами понятие физической величины можно объяснить немного иначе, на примере.

В обоих случаях речь идет о физической величине — массе. Но индивидуальный показатель массы для объектов отличается.

В чем измеряют физическую величину? Примеры физических величин

Физическая величина — это не только масса объекта. Под это определение попадают длина и температура, сила тока и количество вещества, сила света. Все они характеризуют некий объект или явление и выделяют его из множества.

Таким образом, можно назвать несколько параметров и единиц для измерения физической величины:

Во многих странах существуют локальные единицы измерения, которые сильно отличаются от единиц, принятых в других государствах. Однако официальная наука пользуется унифицированной системой мер и весов. Только при необходимости общепринятые единицы переводят в какие-либо другие, принятые в определенной местности.

Источник

Физические величины и их измерение

Содержание:

Измерением физической величины называют совокупность операций, выполняемых с помощью технического средства, хранящего единицу или воспроизводящего шкалу физической величины, заключающихся в сравнении (в явном или неявном виде) измеряемой величины с ее единицей или шкалой с целью получения значения этой величины в форме, удобной для использования.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Физические величины и их измерение

Физическая величина — измеряемое качество, признак или свойство материального объекта или явления, общее в качественном отношении для класса материальных объектов или процессов, явлений, но в количественном отношении индивидуальное для каждого из них. Физические величины имеют род, размер, единицу (измерения) и значение.

Физика — наука о природе

С незапамятных времен люди начали проводить систематические наблюдения за явлениями природы, стремились подметить последовательность происходящих явлений и научились предвидеть ход многих событий в природе, например смену времен года, время разливов рек и многое другое. Эти свои знания они использовали для определения времени посева, уборки урожая и т. д. Постепенно люди убедились в том, что изучение явлений природы приносит им неоценимую пользу.

Тогда появились ученые, которые посвящали свою жизнь изучению явлений природы, обобщали опыт предыдущих поколений. Они записывали результаты наблюдений и опытов, сообщали свои знания ученикам. Вначале учеными были жрецы, которым их знания позволяли держать народ в подчинении. Поэтому записи ученые часто делали в зашифрованном виде, а учеников тщательно отбирали и они должны были хранить свои знания в тайне.

Первые книги о явлениях природы, которые стали достоянием народа, появились, по-видимому, в Древней Греции. Это способствовало быстрому развитию науки в этой стране и появлению многих выдающихся ученых.

Греческое слово «фюзио в переводе означает «природа», поэтому науку о природе стали называть физикой. Начиная с XVII в. происходит быстрое развитие физики. Из нее постепенно выделяются новые науки о природе, например химия. Все науки, изучающие явления природы, стали называть естественными науками.

Многолетнее изучение явлений природы привело ученых к идее о материальности окружающего нас мира. Материя, по определению В. И. Ленина, есть объективная реальность, существующая помимо нашего сознания и данная нам в ощущении. Таким образом, все, реально существующее в природе (а не в нашем воображении), материально. Итак, в основе нашего представления о природе лежит материалистическое миропонимание.

Материя существует не только в форме вещества. Например, радиоволны и свет нельзя назвать веществом. Они представляют собой особую форму материи, называемую электромагнитным полем.

Изучение окружающего нас мира показало, что материя находится в постоянном движении. Любое изменение, происходящее в природе, представляет собой движение материи. Накопленный века

мн опыт убедил ученых, что материя может видоизменяться, но никогда не возникает и не исчезает. Движение материи также может менять свою форму, но само движение материи не создается и не уничтожается. Иначе говоря, окружающий нас мир есть вечно движущаяся и развивающаяся материя. Всеобщей мерой движения материи во всех ее формах является энергия, а неуничтожимость движения материи выражается законом сохранения энергии.

Наиболее общие формы движения материи называются физическими. К ним относятся: механическая, тепловая, электромагнитная, внутриатомная и внутриядерная формы движения материи. Современная физика изучает различные формы движения материи, их взаимные превращения, а также свойства вещества и поля.

Физика и техника

Быстрый прогресс в изучении природы, открытие новых явлений и законов природы способствовали развитию производительных сил общества. Начиная с конца XVIII в. развитие физики сопровождается бурным прогрессом техники. Эту взаимную связь между развитием физики и техники можно проследить на протяжении всей истории нового времени.

Во второй половине XVIII в. и первой половине XIX в. появляются и совершенствуются паровые машины. Одновременно происходит углубленное изучение тепловых процессов и из физики выделяется новая наука — термодинамика. Широкое использование тепловых машин на производстве и транспорте дало повод называть зтот период времени «веком пара».

В конце XIX в. и в начале XX в. появляются и усовершенствуются электрические машины, одновременно совершается множество новых открытий в области электричества и из физики выделяются электротехника, радиотехника и другие науки. Широкое использование электрической энергии в технике дало повод называть это время «веком электричества».

Начиная со второй половины XX в. идет интенсивное изучение свойств атомов и атомных ядер. За это время люди научились получать ядерную энергию и широко использовать ее в технике. Первая в мире атомная электростанция была построена в СССР в 1954 г. Давно уже плавают подводные лодки и корабли, использующие ядерную энергию, строится много атомных электростанций по всему земному шару. Поэтому время, в которое мы живем, можно назвать «атомным веком».

В наше время происходит быстрое освоение космоса человеком. Первый искусственный спутник Земли был запущен в СССР в 1957 г., а в 1970 г. космонавты уже побывали на Луне, межпланетные станции исследуют ближайшие планеты. Таким образом, вторая половина XX в. является началом космической эры.

История развития наук о природе показывает, что именно физика больше всего способствует развитию техники и появлению ее новых областей. Достижения современной физики являются той базой, па которой строится и развивается техника.

Понятие о величине и измерении. Физические величины

Развитие наук о природе, в частности физики, идет по следующему пути. С помощью экспериментов (опытов) накапливается большой фактический материал об определенной группе явлений природы. На основе этого материала создается гипотеза (научное предположение), с единой точки зрения объясняющая эти явления. Справедливость гипотезы проверяется новыми экспериментами. Если правильность гипотезы подтверждается, то на ее основе создается теория, которая должна удовлетворительно объяснять наблюдаемые явления не только с качественной, но и с количественной стороны, а также предсказывать новые явления.

Это означает, что расчеты значений величин с помощью формул, полученных из теории, должны совпадать с результатами измерений этих же значений в экспериментах. Следовательно, эксперименты сопровождаются измерением тех или иных величин.

Все то, что может быть выражено количественно, называют величиной. Так, длина проволоки, скорость движения лодки, «температура воды в стакане являются примерами величин различного рода. Нельзя сравнивать значения разнородных величин, например длину проволоки и скорость движения лодки. А вот сравнить длину проволоки с длиной стола можно. Если при таком сравнении мы установили, что длина проволоки в пять раз больше длины стола, то длина стола является единицей измерения, так как с ней сравнивалась длина проволоки.

Сравнение значений какой-либо величины называется измерением. Чтобы результат измерения некоторой величины был понятен всем, необходимо эту величину сравнивать с одной и той же единицей измерения (например, длину предмета сравнивают с метром). Значение величины, с которым сравниваются все другие значения этой же величины, называют ее единицей измерения. Так, метр является общепринятой единицей длины.

Для каждой величины должна быть установлена своя единица измерения. Число, показывающее, сколько в измеренной величине содержится единиц измерения, называют числовым значением этой величины.

Величины, характеризующие физические свойства материи или характерные особенности физических явлений природы, называются физическими величинами. (Например, длина, время, скорость, мощность и т. д.) Числовые значения физических величин нужно писать с наименованиями их единиц, например: 2,4 метра, 4,5 секунды, или сокращенно: 2,4 м, 4,5 с.

Сначала в каждой стране пользовались своими единицами измерения, но в конце XVIII в. во Франции была создана метрическая система мер, которая в настоящее время применяется во всем мире.

При создании этой системы были установлены единицы измерения: длины — метр, массы — килограмм, времени — секунда.

Прямое и косвенное измерения

Выясним теперь, как находят числовое значение величины при измерении. Измерять длину куска ткани можно, прикладывая к нему метр, как это делается в магазинах. На рис. 1.1 показана миллиметровая сетка, на которой изображен прямоугольник со сторонами l = 12 мм и b = 10 мм. Площадь прямоугольника также можно измерить, укладывая внутри него образец единицы площади, например 1 . Подсчет показывает, что внутри прямоугольника содержится 120 квадратов со стороной в 1 мм, т. е. площадь прямоугольника равна 120 .

Измерение, при котором значение величины определяется непосредственным сравнением с ее единицей, называют прямым измерением. Приведенные выше примеры являются прямыми измерениями длины и площади.

Однако прямое измерение далеко не всегда дает достаточно точный результат, кроме того, оно не всегда выполнимо и удобно. На рис. 1.1 изображена окружность диаметром 7 мм.

Если нужно найти длину l этой окружности, то удобнее измерить не саму окружность, а ее диаметр d и затем вычислить l по формуле , или.

Если требуется измерить площадь круга, то неудобно подсчитывать число квадратных миллиметров внутри окружности. Проще и точнее, измерив диаметр, вычислить эту площадь по формуле , или . Измерив длину и ширину прямоугольника, его площадь можно вычислить по формуле s = lb.

Измерение, при котором числовое значение величины находится по формуле путем вычисления, называется косвенным измерением. На практике (и в науке и в технике) чаще всего приходится выполнять косвенные измерения.

Звездное небо и его видимое вращение

Когда мы смотрим на безоблачное ночное небо, нам кажется, что все небесные тела находятся на внутренней поверхности некоторой сферы, которую мы обычно называем небесным сводом или небом. Чтобы легче было ориентироваться на небе, еще в древности наиболее яркие звезды были условно объединены в группы — созвездия; позднее ПОД созвездиями стали понимать участки звездного неба.

Если наблюдать за звездным небом в течение нескольких часов, легко заметить, что весь небесный свод со всеми находящимися на нем светилами вращается вокруг воображаемой оси, проходящей через точку, где находится наблюдатель, и некоторую неподвижную точку на небосводе, называемую полюсом мира (рис. 1.2). Это видимое вращение небесного свода называют суточным движением, так как одно полное обращение совершается за сутки.

Полюс мира в северном полушарии почти совпадает с Полярной звездой (звезда в Малой Медведице). Ее легко найти на небе, продолжив мысленно линию, соединяющую крайние звезды и ковша Большой Медведицы (рис. 1.2).

Ось видимого вращения небесной сферы называют осью мира. Нетрудно понять, что ось мира параллельна оси вращения Земли, а угол между осью мира и плоскостью горизонта равен

географической широте данной местности. Так, в районе Северного полюса Земли Полярная звезда находится над головой (ось мира вертикальна), а вблизи экватора — у самого горизонта.

Угловые измерения на небе

Большинство объектов, которые исследуются в астрономии, недоступно непосредственному наблюдению, поэтому все сведения о них могут быт ь получены только на основе всестороннего изучения приходящего от них света (или других излучений). О том, как анализируется свет качественно и количественно, будет рассказано дальше. Пока что нам важно, что по направлению луча света, приходящего от небесного тела (светила), можно установить его положение на небе. Это делается путем угловых измерений.

Так, угол между зрительной трубой, направленной на небесное тело, и плоскостью горизонта называется его высотой над горизонтом. Угол между направлениями на две звезды определяет угловое расстояние между ними. Разумеется, угловое расстояние между небесными телами характеризует только их взаимное расположение на небе. Если, например, две звезды находятся друг от друга на малом угловом расстоянии и кажутся расположенными рядом, то это вовсе не означает, что они действительно близки между собой. Одна из них может быть во много раз дальше от Земли, чем другая. Фотографируя звездное небо и измеряя на фотографиях расстояния между звездами, астрономы составляют звездные атласы и карты, схемы и списки точных координат звезд.

Угловые измерения на небе производят не только при разнообразных астрономических наблюдениях, но и широко иcпользуют с давних времен в навигации для ориентирования по Солнцу и звездам. В настоящее время по Солнцу и звездам осуществляют ориентацию спутников и космических кораблей.

Угловые измерения необходимы также для определения размеров небесных тел. Нетрудно понять, что видимые размеры светила зависят от расстояния до него. Например, угловой диаметр Солнца, т. е. угол между направлениями на диаметрально противоположные точки солнечного диска, составляет 0,5°. Луна примерно в 400 раз меньше Солнца, но во столько же раз ближе к Земле; поэтому она имеет такой же угловой диаметр и во время солнечных затмений может полностью закрыть от нас диск Солнца. Звезды же так далеки от нас, что в самые сильные телескопы видны в виде точек, хотя известно, что многие из них гораздо больше Солнца.

Определение расстояний до небесных тел на основе измерения параллаксов

При определении расстояний до небесных тел мы не можем выполнять прямые измерения, и поэтому для этой цели используют различные косвенные методы. Важнейший из них — метод тригонометрического параллакса.

Если смотреть на какой-либо предмет из разных точек (например, на кончик карандаша, поочередно закрывая то левый, то правый глаз), то можно заметить, что его положение на фоне более далеких предметов изменяется. Изменение направления на предмет при перемещении наблюдателя называют параллаксом. Расстояние между точками, из которых производится наблюдение, называют базисом (в рассмотренном примере это расстояние между глазами).

Измерив параллакс, можно вычислить расстояние до удаленного объекта. Подобный принцип используется в дальномере. В этом приборе базисом служит расстояние между двумя объективами. Определив угол р (рис. 1.3) между направлениями на объект S из точек A и В и зная базис АВ = а, можно вычислить расстояние D до объекта.

Заметим, что из точки, где расположен объект S, базис виден под углом р. Расстояние D до объекта всегда несравненно больше базиса а, и угол р всегда очень мал. Если базис перпендикулярен к направлению на объект, то его можно принять равным длине дуги окружности с радиусом D. Тогда а = Dр, где угол р выражен в радианах. Отсюда

С помощью измерения параллаксов вычисляют расстояния до небесных тел в астрономии. Для измерения расстояния до какой-либо планеты можно определить ее положение на фоне звезд одновременно из двух обсерваторий, расстояние между которыми и будет определять базис. Однако на практике гораздо удобнее производить наблюдение из одной обсерватории в разное время суток, используя перемещение обсерватории при вращении Земли вокруг своей оси. Измеренный таким путем параллакс для определенности условились пересчитывать для одного и того же базиса, равного радиусу земного шара.

При определении расстояния до звезд используют перемещение Земли по орбите, поскольку земные расстояния оказываются в этом случае слишком малы, чтобы служить базисом. С помощью телескопа обычно фотографируют одну и ту же область неба с промежутком времени в полгода. Измерив смещение выбранной звезды относительно более далеких звезд, определяют ее параллакс и вычисляют расстояние до нее. Базисом при этом служит расстояние между двумя диаметрально противоположными точками земной орбиты, из которых проводились наблюдения. Измеренный параллакс звезд условились пересчитывать для одного и того же базиса, равного большой полуоси земной орбиты (напомним, что орбита Земли представляет собой эллипс). Определенный таким образом параллакс называют годичным параллаксом звезды. Он равен углу, под которым со звезды видна большая полуось земной орбиты, перпеникулярная направлению на звезду. Если угол р выразить в секундах дуги, то, поскольку 1 рад=206265«, получим:

Подставив в (1.2) вместо а его значение, можно подсчитать, что годичному параллаксу в 1« соответствует расстояние D=3,08 . 10 16 м. Эта величина используется в астрономии в качестве единицы длины и называется парсек (пк) : 1пк = 3,08 . 10 16 м. Расстояние до звезды в парсеках равно обратной величине ее годичного параллакса, выраженного в секундах дуги:

Годичный параллакс самой близкой звезды (альфа Центавра) оказался равным 0,75«. Расстояние до нее в парсеках D=(1/0,75) пк = 1,33 пк.

Основные единицы времени и их связь с движением Земли

Одной из важнейших физических величин является время. Жизнь на Земле тесно связана с периодическим движением Солнца по небосводу, поэтому с давних времен счет времени и определение единиц времени связаны с этим движением. Одна из таких единиц — солнечные сутки — представляет собой промежуток времени между двумя последовательными прохождениями Солнца через наивысшую точку над горизонтом (между двумя полуднями). Для измерения больших промежутков времени используется год — время одного оборота Земли вокруг Солнца. Для измерения малых промежутков времени сутки разделили на 24 часа, час — на 60 минут, минуту — на 60 секунд. Таким образом, секунда составляет 1/86 400 часть солнечных суток.

Долгое время астрономические наблюдения были единственным средством точного измерения времени. С изобретением часов люди получили возможность воспроизводить единицы времени. По мере совершенствования часов все более возрастала их точность; это позволило определить, что суточное вращение Земли происходит не совсем равномерно и длительность суток слегка колеблется. Поэтому для установления единицы времени были использованы средние за год солнечные сутки, причем для определенности был выбран 1900 г., так как оказалось, что продолжительность года уменьшается примерно на полсекунды за столетие. Итак, было принято, что секунда составляет 1/86 400 долю средних солнечных суток 1900 г.

Такое определение эталона секунды, являющейся в физике основной единицей времени, неудобно, так как этот эталон нельзя точно воспроизвести. Развитие атомной физики позволило установить новый эталон секунды, который будет рассмотрен в § 35.16.

Правило вывода единиц физических величин из формул. Международная система единиц СИ

В физике встречается очень много различных величин, каждая из которых имеет свою единицу измерения. Произвольный выбор этих единиц сильно осложняет расчеты, так как в формулах, выражающих связь между различными физическими величинами, появляются числовые коэффициенты, зависящие только от выбора единиц измерения.

Таким образом, при произвольном выборе единиц все физические формулы надо писать с некоторыми коэффициентами пропорциональности . Например, формулу второго закона Ньютона надо записывать в виде , а формулу для работы силы F на отрезке пути s в виде и т. д.

Однако в большинстве формул от этих коэффициентов можно избавиться, т. е. сделать их равными единице, если ввести произвольные единицы только для некоторых физических величин, принятых за основные, а единицы остальных физических величин выводить из формул. Так, в механике можно принять за основные величины длину, массу, время и для них выбрать единицы (например, метр, килограмм, секунда), а единицы остальных механических величин вывести из формул. Выведем, например, единицы силы и работы.

В формуле второго закона Ньютона та коэффициент будет равен единице, если при массе, равной единице, и ускорении, равном единице, сила тоже будет равна единице. Имея единицы массы и ускорения, можно выбрать единицу силы так, чтобы это условие выполнялось. Тогда формулу второго закона Ньютона можно писать без . Подберем теперь нужную нам единицу силы. Для этого подставим на место m и a их единицы с сокращенными наименованиями и выполним алгебраические действия как над числами, так и над наименованиями:

Аналогично для единицы работы получим

Если величина, для которой ищут единицу, не выражена в явном виде, то, рассматривая формулу как уравнение, нужно найти эту величину в буквенном виде, а затем уже подставлять известные единицы измерения. Например, пусть нужно вывести единицу скорости из формулы . Тогда пишем

Сформулируем теперь правило вывода единиц физических величин. Чтобы вывести новую единицу какой-либо физической величины, нужно: 1) подобрать формулу, содержащую эту величину, в которой единицы всех других величин известны; 2) алгебраически найти из формулы буквенное выражение этой величины; 3) в полученное выражение подставить все известные единицы измерения с их размерностями; 4) выполнить все требуемые алгебраические действия как над числами, так и над размерностями; 5) принять полученный результат за искомую единицу и дать ей название.

Для примера выведем теперь единицу мощности:

1) подбираем формулу: A = Nt 2) находим из этой формулы N : N = A/t

3) подставляем единицы работы и времени: N=1 Дж/1 с = (1 кг . м 2 /с 2 )/1 с; 4) выполняем действия: N = 1 кг . м 2 /с 3 ; 5) принимаем этот результат за единицу мощности и даем ей название ватт (Вт):

Те единицы, которые устанавливаются произвольно и независимо друг от друга, например по международному соглашению, называются основными, а те, которые выводятся из формул, называются производными (от основных). Совокупность основных единиц с выведенными из них производными единицами называется системой единиц.

Оказалось, что для получения системы механических единиц целесообразно установить три основные единицы, а все остальные выводить из формул. B приведенных выше примерах основными единицами были: единица длины — 1 м, единица массы — 1 кг и единица времени — 1с. Здесь сокращенные названия м, кг, с называются размерностями основных единиц измерения. Результат действий над этими размерностями, показывающий, как производная единица получилась из основных, называется размерностью производной единицы измерения.

Очевидно, изменяя основные единицы (для одних и тех же физических величин, принятых за основные) или выбирая другие физические величины в качестве основных, можно получить много различных систем единиц. Поскольку физические формулы пишут без коэффициентов , вычисления будут давать правильный результат только в том случае, когда все числовые значения величин будут подставляться в одной и той же системе единиц.

В настоящее время при расчетах следует пользоваться Международной системой единиц, сокращенно — СИ (система интернациональная). Это единая универсальная система, связывающая единицы механических, тепловых, электрических и других физических величин. Она построена на семи основных единицах:

1) единица длины — 1 метр (м);

2) единица массы — 1 килограмм (кг);

3) единица времени — 1 секунда (с);

4) единица температуры — 1 кельвин (К);

5) единица силы тока—1 ампер (А);

6) единица силы света — 1 кандела (кд);

7) единица количества вещества — 1 моль (моль).

Точные определения этих единиц будут приведены дальше при изложении соответствующего материала.

Плотность вещества

Измерение массы и объема тел, сделанных из одинакового вещества, показывает, что их масса прямо пропорциональна объему:

Здесь коэффициент К зависит от выбора единиц измерения и от рода вещества, так как масса тела, кроме объема, зависит еще от рода вещества, из которого состоит тело. Поэтому коэффициент К в формуле (1.4) можно представить в виде произведения двух сомножителей: , выражающего зависимость массы от выбора единиц измерения, и , выражающего зависимость массы от рода вещества тела: . Тогда формула (1.4) примет вид

Как говорилось выше, в формуле (1.5) можно не писать, если воспользоваться ею для вывода новой единицы измерения. Поэтому формулу (1.5) записывают следующим образом»

Величина , характеризующая зависимость массы тела от рода вещества и внешних условий, называется плотностью вещества. Плотность измеряют массой вещества в единице объема:

Объем тела меняется при изменении давления и температуры. Это и означает, что плотность зависит от внешних условий. Теперь выведем единицу плотности:

В СИ за единицу плотности принимают плотность такого вещества, которое в объеме 1 м 3 имеет массу 1 кг. При расчетах плотность вещества берут из таблиц.

Услуги по физике:

Лекции по физике:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник