Для чего нужны комплексные числа в математике кратко
Откуда есть пошло комплексное число
В современной математике комплексное число является одним из фундаментальнейших понятий, находящее применение и в «чистой науке», и в прикладных областях. Понятно, что так было далеко не всегда. В далекие времена, когда даже обычные отрицательные числа казались странным и сомнительным нововведением, необходимость расширения на них операции извлечения квадратного корня была вовсе неочевидной. Тем не менее, в середине XVI века математик Рафаэль Бомбелли вводит комплексные (в данном случае точнее сказать, мнимые) числа в оборот. Собственно, предлагаю посмотреть, в чем была суть затруднений, доведших в итоге солидного итальянца до подобных крайностей.
Существует распространенное заблуждение, что комплексные числа потребовались для того, чтобы решать квадратные уравнения. На самом деле, это совершенно не так: задача поиска корней квадратного уравнения никоим образом введение комплексных чисел не мотивирует. Вот совершенно.
Давайте убедимся сами. Всякое квадратное уравнение можно представить в виде: 
.
Геометрически, это означает, что мы хотим найти точки пресечения некоторой прямой и параболы
Я тут даже картинку сделал, для иллюстрации.
Как нам всем хорошо известно из школы, корни квадратного уравнения (в указанных выше обозначениях) находятся по следующей формуле:
Оказываются возможными 3 варианта:
1. Подкоренное выражение положительно.
2. Подкоренное выражение равно нулю.
3. Подкоренное выражение отрицательно.
В первом случае имеются 2 различных корня, во втором два совпадающих, в третьем уравнение «не решается». Все эти случаи имеют вполне наглядную геометрическую интерпретацию:
1. Прямая пересекает параболу (синяя прямая на рисунке).
2. Прямая касается параболы.
3. Прямая не имеет с параболой общих точек (сиреневая прямая на рисунке).
Ситуация проста, логична, непротиворечива. Пытаться извлекать квадратный корень из отрицательного числа нет совершенно никаких оснований. Никто и не пытался.
Обстановка существенно изменилась, когда пытливая математическая мысль добралась до кубических уравнений. Чуть менее очевидно, используя некоторую несложную подстановку, всякое кубическое уравнение можно свести к виду: . С геометрической точки зрения ситуация похожа на предыдущую: мы ищем точку пересечения прямой и кубической параболы.
Взгляните на картинку:
Существенное отличие от случая квадратного уравнения в том, что какую бы прямую мы не взяли, она всегда пересечет параболу. Т.е., уже из чисто геометрических соображений, кубическое уравнение всегда имеет хотя бы одно решение.
Найти его можно воспользовавшись формулой Кардано:
где .
Немного громоздко, но пока, вроде бы, все в порядке. Или нет?
Вообще, формула Кардано — это яркий пример «принципа Арнольда» в действии. И что характерно, Кардано никогда на авторство формулы не претендовал.
Вернемся, однако, к нашим баранам. Формула замечательная, без преувеличение великое достижение математики начала-середины XVI века. Но есть у нее один нюанс.
Возьмем классический пример, который рассматривал еще Бомбелли: .
Внезапно, ,
и, соответственно, .
Приплыли. А формулу жалко, а формула-то хорошая. Тупик. При том, что решение у уравнения, безусловно, есть.
Идея Рафаэля Бомбелли заключалась в следующем: давайте прикинемся шлангом и сделаем вид, что корень из отрицательного — это какое-то число. Мы, конечно, знаем, что таких чисел нет, но тем не менее, давайте представим, что оно существует и его, как обычные числа, можно складывать с другими, умножать, возводить в степень и т.п.
Используя подобный подход, Бомбелли установил, в частности, что ,
и .
Давайте проверим: .
Заметьте, в выкладках никаких предположений о свойствах квадратных корней из отрицательных чисел не предполагалось, кроме упомянутого выше допущения, что они ведут себя как «обычные» числа.
В сумме получаем . Что вполне себе правильный ответ, который элементарно проверяется прямой подстановкой. Это был настоящий прорыв. Прорыв в комплексную плоскость.
Тем не менее, подобные выкладки выглядят как некоторая магия, математический фокус. Отношение к ним, как к некоему трюку, сохранялось среди математиков еще очень долго. Собственно, придуманное Рене Декартом для корней из отрицательных название «мнимые числа» вполне отражает отношение математиков тех времен к таким развлечениям.
Однако, время шло, «трюк» применялся с неизменным успехом, авторитет «мнимых чисел» в глазах математического общества рос, сдерживаемый, однако, неудобством их использования. Лишь получение Леонардом Эйлером (кстати, это именно он ввел ныне общеупотребительное обозначение для мнимой единицы) знаменитой формулы
открыло комплексным числам дорогу в самые различные области математики и ее приложений. Но это уже совсем другая история.
Статья на тему «Комплексные числа»
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
1.Для чего нужны комплексные числа?
В любой науке любая математика должна по идее быть математикой комплексных чисел. Дело в том, что из всех наук, только физика наиболее математизирована. И математические методы наиболее сильно проникли в физику. Комплексные числа также используются в исследовании течения воды, вычерчивании географических карт, конструривании ракет и самолетов.
Комплексные числа, как и отрицательные, возникли из внутренней потребности самой математики – из практики и теории решения алгебраических уравнений. С комплексными числами впервые математики встретились при решении квадратных уравнений. До 16 века математики всего мира, не находя приемлемого толкования для комплексных корней, возникавших при решении квадратных уравнений, объявляли их ложными и не принимали во внимание. Только в начале 19 века, когда уже была выяснена роль комплексных чисел в различных областях математики, была разработана очень простая и естественная их геометрическая интерпретация, позволившая уяснить геометрический смысл операций над комплексными числами. Тем самым был положен конец сомнениям в законном и полезном применении комплексного числа.
2.Действия над комплексными числами в алгебраической форме.
Над комплексными числами в алгебраической форме можно выполнять следующие действия.
Умножение комплексных чисел обладает следующими свойствами:
3º. Дистрибутивность умножения относительно сложения:
На практике умножение комплексных чисел производят по правилу умножения суммы на сумму и выделения действительной и мнимой части.
В следующем примере рассмотрим умножение комплексных чисел двумя способами: по правилу и умножением суммы на сумму.
На практике частное комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю.
В следующем примере выполним деление по формуле и правилу умножения на число, сопряженное знаменателю.
Поэтому, чтобы возвести число i в целую положительную степень, надо показатель степени разделить на 4 и возвести i в степень, показатель которой равен остатку от деления.
3.Извлечение корней из комплексных чисел.
Вычислить 
Можно извлечь два корня:
Что и требовалось проверить.
4.Тригонометрическая форма комплексного числа
Модулем комплексного числа 
называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.
Модуль комплексного числа обозначают 
или 
По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: 
. Данная формула справедлива для любых значений « а » и « b ».
Аргументом комплексного числа называется угол 
между положительной полуосью действительной оси 
и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: 
.
. Для нахождения аргумента получается следующая формула:
.
Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-й и не 4-й координатной четверти, то формула будет немного другой.
Доклад на тему «Комплексные числа»
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Название работы: «Комплексные числа»
2. История развития комплексных чисел.
3. О комплексных числах.
4. Соглашение о комплексных числах
5. Сложение комплексных чисел
7. Умножение комплексных чисел.
8. Деление комплексных чисел.
9. Модуль и аргумент комплексного числа.
10. Тригонометрическая форма комплексного числа.
Решение многих задач физики и техники приводит к квадратным уравнениям с отрицательным дискриминантом. Эти уравнения не имеют решения в области действительных чисел. Но решение многих таких задач имеет вполне определенный физический смысл. Значение величин, получающихся в результате решения указанных уравнений, назвали комплексными числами. Комплексные числа широко использовал отец русской авиации Н. Е. Жуковский (1847 1921) при разработке теории крыла, автором которой он является. Комплексные числа и функции от комплексного переменного находят применение во многих вопросах науки и техники.
История развития комплексных чисел.
Теория комплексных чисел развивалась медленно: ещё в 18 веке крупнейшие математики мира спорили о том, как находить логарифмы комплексных чисел. Хотя с помощью комплексных чисел удалось получить много важных фактов, относящихся к действительным числам, но самое существование комплексных чисел многим казалось сомнительным. Исчерпывающие правила действий с комплексными числами дал и в 18 веке русский академик Эйлер – один из величайших математиков всех времён и народов. На рубеже 18 и 19 веков было указано Весселем (Дания) и Арганом (Франция) геометрическое изображение комплексных чисел. Но на работы Весселя и Аргана не обратили внимания, и лишь в 1831 г. когда тот же способ был развит великим математиком Гауссом (Германия), он стал всеобщим достоянием.
О комплексных числах.
В связи с развитием алгебры потребовалось ввести сверх прежде известных положительных и отрицательных чисел числа нового рода. Они и называются комплексными.
“Мнимые” числа составляют частный вид комплексных чисел (когда а = 0).
С другой стороны, и действительные числа являются частным видом комплексных чисел (когда b = 0).
Долгое время не удавалось найти такие физические величины, над которыми можно выполнять действия, подчинённые тем же правилам, что и действия над комплексными числами – в частности правилу (1). Отсюда названия: “мнимая единица”, “мнимое число” и т.п. В настоящее время известен целый ряд таких физических величин, и комплексные числа широко применяются не только в математике, но также и в физике и технике.
Правило каждого действия над комплексными числами выводится из определения этого действия. Но определения действий над комплексными числами не вымышлены произвольно, а установлены с таким расчетом, чтобы согласовались с правилами действий над вещественными числами. Ведь комплексные числа должны рассматриваться не в отрыве от действительных, а совместно с ними.
Соглашение о комплексных числах.
Действительное число а записывается также в виде a + 0 i (или a – 0 i ).
Запись 3 + 0 i обозначает то же, что запись 3. Запись –2 + 0 i означает –2.
Сложение комплексных чисел
Это определение подсказывается правилами действий с обычными многочленами.
Пример 2. (2 + 0i) + (7 + 0i) = 9 + 0i. Так как запись 2 + 0 i означает то же, что и 2 и т. д., то наполненное действие согласуется с обычной арифметикой (2 + 7=9).
Пример 3. (0 + 2i) + (0 + 5i) = 0 + 7i, т. е. 2i + 5i = 7i
Вычитание комплексных чисел.
Пример 2. (3 + 2i) – (-3 + 2i) = 6 + 0i = 6
Умножение комплексных чисел.
О п р е д е л е н и е. Произведением комплексных чисел a + bi и a ’ + b ’ i
называется комплексное число
Пример 1. (1 – 2i)(3 + 2i) = 3 – 6i + 2i – 4i 2 = 3 – 6i + 2i + 4 = 7 – 4i.
Пример 2. (a + bi)(a – bi) = a 2 + b 2
Пример 2 показывает, что произведение сопряженных комплексных чисел есть действительное и притом положительное число.
Деление комплексных чисел.
В соответствии с определением деления действительных чисел устанавливается следующее определение.
Если делитель не равен нулю, то деление всегда возможно, и частное единственно. На практике частное удобнее всего находить следующим образом.
Пример 1. Найти частное (7 – 4 i ) :(3 + 2i).
Пример 1 предыдущего параграфа даёт проверку.
Модуль и аргумент комплексного числа.
r = | a + bi | = a 2 + b 2
Модуль действительного числа совпадает с его абсолютным значением. Сопряжённые комплексные числа a + bi u a – bi имеют один и тот же модуль.
Тригонометрическая форма комплексного числа.
a = r cos q; b = r sin q.
Поэтому всякое комплексное комплексное число можно представить в виде r ( cos q + i sin q ), где r > 0.
Это выражение называется нормальной тригонометрической формой или, короче, тригонометрической формой комплексного числа.
Комплексные числа
Формы
Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:
Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.
Изображение
Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:
Вычислить сумму и разность заданных комплексных чисел:
Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел:
Аналогично выполним вычитание чисел:
Выполнить умножение и деление комплексных чисел:
Так, теперь разделим первое число на второе:
Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки:
Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы:
Для возведения в квадрат достаточно умножить число само на себя:
Пользуемся формулой для умножения, раскрываем скобки и приводим подобные:
В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую.
Вычисляем значение модуля:
Найдем чем равен аргумент:
$$ \varphi = arctg \frac<3> <3>= arctg(1) = \frac<\pi> <4>$$
Записываем в тригонометрическом виде:
Преобразуем в алгебраическую форму для наглядности:
Представим число в тригонометрической форме. Найдем модуль и аргумент:
Используем знакомую формулу Муавра для вычисления корней любой степени:
Что такое комплексные числа
Первый урок по комплексным числам. Сегодня мы разберём:
Если же вас интересует тригонометрическая форма записи комплексного числа, либо извлечение корней из комплексных чисел — этим темам посвящены отдельные уроки.
Сегодня — лишь самое главное. Но не самое простое.:)
0. Краткая вводная
Когда-то нам хватало натуральных чисел:
Всё было прекрасно: «У тебя 5 бананов, у меня ещё 3 — итого у нас 5 + 3 = 8 бананов». Сумма двух натуральных чисел всегда даёт новое натуральное число (говорят, что операция сложения замкнута на множестве натуральных чисел).
Но вот на сцену выходит вычитание — и натуральных чисел стало недостаточно. Например разность 3 − 5 = −2 уже не будет натуральным. Так появились целые числа (натуральные, им противоположные и ноль):
Дальше к делу подключились операции умножения и деления. Да, произведение двух целых чисел всё ещё целое, но вот деление приводит к образованию дробей. Например, 1 : 2 или 5 : 4 уже нельзя записать целым числом. Так появилось множество рациональных чисел или множество дробей:
Это был настоящий триумф для древней математики, и в тот момент казалось, что ничего больше уже изобрести нельзя. Да и зачем?
Проблема пришла откуда не ждали. В какой-то момент классическое умножение «разрослось» до возведения в степень:
Тут-то и выяснилось, что возведение рационального числа в натуральную степень всё ещё будет рациональным числом. Но вот обратная операция — извлечение корня — выносит нас за пределы рациональных чисел:
\[\sqrt<2>=1,41421. \notin \mathbb\]
Так появилось множество действительных чисел — множество бесконечных десятичных дробей, которые могут быть периодическими (и тогда это обычное рациональное число) и непериодическими (такие числа называют иррациональными, и их неизмеримо больше).
Казалось бы: ну вот теперь точно всё! Что ещё нужно для счастья? Проблема в том, что на множестве действительных чисел нельзя извлечь даже самый простой квадратный корень из отрицательного числа:
Однако законы физики (особенно электродинамика и вообще всё, где есть слово «динамика») как бы намекали, что множество содержательных процессов протекает там, где привычные корни не извлекаются. А значит, следует расширить множество действительных чисел так, чтобы такие корни всё же извлекать.
И тут открылись врата в Ад.
1. Комплексная единица
Начнём с ключевого определения.
Однако в остальном это такое же число, как и все остальные. Комплексные единицы можно складывать, умножать, их можно комбинировать с «нормальными» числами:
2. Стандартная форма записи комплексных чисел
А теперь всё по-взрослому.
Определение. Комплексное число — это любое число вида
\[\begin
\[\begin
И напротив: существуют «чисто мнимые» числа, у которых вообще нет действительной части. Та же комплексная единица, например:
\[\begin
Таким образом, действительные числа являются частным случаем комплексных. Подобно тому как рациональные числа являются частным случаем действительных (в конце концов, рациональные числа — те же десятичные дроби, но с дополнительным условием: они периодические).
2.1. Равенство комплексных чисел
В самом деле, пусть некоторое число записано двумя способами:
Соберём все действительные слагаемые слева, а мнимые — справа:
Слева мы видим действительное число. Значит, справа тоже должно стоять действительное число. Единственная ситуация, в которой это возможно:
Получается, что справа от знака равенства стоит ноль. Следовательно, слева тоже ноль:
Следовательно, исходные записи совпадают.
Поэтому имеет смысл следующее определение.
Определение. Два комплексных числа равны друг другу тогда и только тогда, когда равны их действительные части, а также равны их мнимые части:
Если хотя бы одна из частей не равна, то и сами числа не равны.
Поскольку от перестановки слагаемых сумма не меняется (сложение чисел — настолько суровая операция, что какие-то там «комплексные единицы» никак не нарушают его коммутативности), мы можем записать:
А вот перестановка мнимой и действительной части (если эти части разные) немедленно ведёт к нарушению равенства:
К координатной плоскости мы ещё вернёмся. А пока определим правила сложения и вычитания комплексных чисел.
3. Сложение и вычитание комплексных чисел
Выше мы проводили аналогию между комплексными числами и многочленами. Идём по этому пути дальше и вспоминаем, что многочлены можно складывать, группируя слагаемые и приводя подобные:
Точно так же можно определить и сложение (да и вычитание) двух комплексных чисел. Всё просто:
Другими словами, при сложении комплексных чисел отдельно складываются их действительные части и отдельно — мнимые. То же самое для вычитания.
Не нужно учить эти формулы. Дальше будут формулы умножения и деления — они ещё сложнее. Нужно понять ключевую идею: мы работаем с комплексными числами точно так же, как с многочленами. С небольшим дополнением: все степени комплексной единицы выше первой «сжигаются» прямо по определению самой единицы:
Небольшое замечание. В отличие от математики 5—6 классов, в серьёзной «взрослой» алгебре нет такого понятия как «вычитание». Зато есть понятие противоположного элемента и алгебраической суммы:
Всё это в полной мере относится и к комплексным числам. Там тоже есть противоположные:
Есть ноль (нейтральный элемент по сложению):
\[\begin
В общем, множество комплексных чисел — это абсолютно «нормальное» множество с понятной операцией сложения. Буквально через пару минут мы определим и умножение, но сначала давайте всё-таки запишем определение самого множества комплексных чисел.
Записывается это так:
Не пугайтесь, когда увидите подобную запись где-нибудь в учебнике алгебры. По сути, это краткая запись всего того, о чём мы говорили выше. Ничего нового мы здесь не узнали.
А вот что действительно представляет интерес — сейчас узнаем.:)
4. Геометрическая интерпретация комплексных чисел
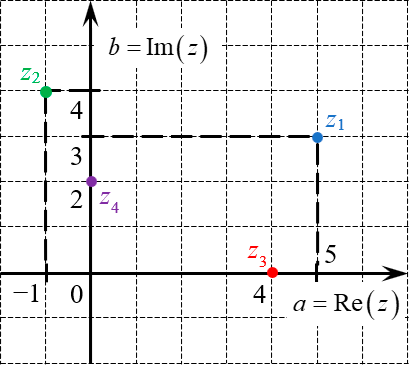
Такие упорядоченные пары удобно рассматривать как координаты точек. По горизонтали (ось абсцисс) мы будем отмечать действительную часть числа, а по вертикали (ось ординат) — мнимую.
Определение. Комплексная плоскость — декартова система координат, где по горизонтали отмечается действительная часть комплексного числа, а по вертикали — мнимая.
Рассмотрим несколько примеров. Отметим на комплексной плоскости числа:
4.1. Ещё раз о сложении и вычитании
Такое представление чисел — в виде точек на комплексной плоскости — называется геометрической интерпретацией. Числа в таком виде удобно складывать и вычитать. По сути, всё сводится к сложению обычных векторов.
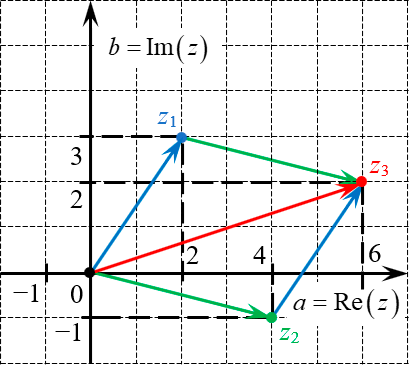
Допустим, мы хотим сложить два числа:
Отметим эти числа на комплексной плоскости, построим векторы из начала координат с концами в отмеченных точках, а затем просто сложим эти векторы (по правилу треугольника или параллелограмма — как пожелаете):
Координаты новой точки: (6; 2). Следовательно, сумма равна:
Аналогичный результат можно получить и алгебраически:
Как видим, алгебраические выкладки заняли гораздо меньше времени и места. Уже хотя бы потому что не потребовалось чертить систему координат.:)
Зачем же тогда нужна комплексная плоскость и геометрическая интерпретация? Всё встанет на свои места буквально через пару уроков, когда мы рассмотрим тригонометрическую форму записи комплексных чисел, а также будем извлекать из этих чисел корни.
А чтобы подготовиться к этим урокам, рассмотрим ещё два ключевых определения.
5. Комплексно-сопряжённые и модуль числа
Для начала вспомним школьную алгебру. Работа с многочленами, 7-й класс:
называется разностью квадратов и является одной из формул сокращённого умножения.
В математических классах с помощью сопряжённых искали обратные числа, чтобы затем решать сложные показательные и логарифмические уравнения:
Теперь настало время комплексных чисел. В них тоже можно ввести понятие сопряжённых.
5.1. Комплексно-сопряжённые
Комплексно-сопряжённые числа отмечаются чертой сверху.
Рассмотрим несколько примеров:
Видим, что комплексно-сопряжённое к «чисто мнимому» числу есть число, ему противоположное. А комплексно-сопряжённое к действительному числу есть само это число.
Зачем нужны комплексно-сопряжённые? Вспомним всё ту же формулу разности квадратов:
Итак, произведение числа на комплексно-сопряжённое даёт сумму квадратов действительной и мнимой части. Это ключевое свойство комплексно-сопряжённых, и оно позволяет нам рассмотреть следующее определение.
5.2. Модуль комплексного числа
Снова вспомним школьную алгебру. Модуль действительного числа определяют так:
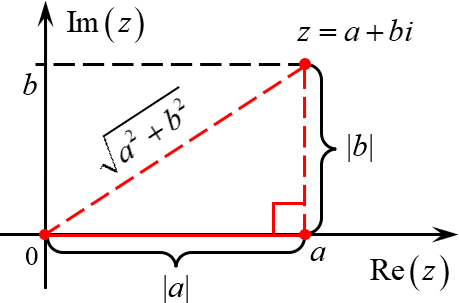
Ключевая идея: модуль числа — это всегда неотрицательная величина, равная расстоянию от точки, соответствующей этому числу, до начала отсчёта. Но всё это происходит на числовой прямой. На комплексной плоскости к делу подключается теорема Пифагора.
Вновь обратимся к геометрической интерпретации:
\[b=0\Rightarrow \left| z \right|=\sqrt<<^<2>>>\]
Получается, что на множестве комплексных чисел нельзя ввести привычные нам понятия «больше» или «меньше». Поскольку каждое число характеризуется двумя независимыми параметрами (действительной и мнимой частью), нет универсальной меры, нет отношения порядка.
Можно считать это фундаментальным законом природы. Когда мы держим в голове больше одного параметра, нет больше универсального критерия успеха:
Оценка одного и того же события будет меняться в зависимости от настроения и наших предпочтений.
Модуль числа нам пригодится в следующем уроке. А вот комплексно-сопряжённые мы будем применять уже сейчас.
6. Умножение и деление комплексных чисел
Комплексные числа можно не только складывать и вычитать, но даже умножать и делить друг на друга.
6.1. Умножение
С умножением ничего особенного.
\[\begin
Как видим, произведение комплексных чисел вновь даёт комплексное число.
Как и в случае со сложением, не нужно учить эти формулы наизусть. Лучше просто потренироваться и понять сам механизм:
Достаточно решить 10—15 таких примеров — и никакие специальные формулы и определения вам больше не понадобятся. То же самое и с делением.
6.2. Деление
Финальный бросок — попробуем разделить одно комплексное число на другое. Разумеется, делитель не должен быть нулём, иначе частное не определено.
Частное комплексных чисел вновь будет комплексным числом.
Саму формулу не нужно запоминать. Достаточно лишь отметить для себя, что мы умножили числитель и знаменатель дроби на комплексно-сопряжённое к знаменателю. Само деление можно выполнять напролом:
Тем не менее, даже после основательной тренировки умножение и особенно деление комплексных чисел остаётся трудоёмкой операцией, где можно допустить множество ошибок. Поэтому для таких операций (а также для кое-чего гораздо более серьёзного) математики придумали другую форму записи комплексных чисел — тригонометрическую. С ней мы и познакомимся на следующем уроке.:)