Для чего нужны координаты

§ 14. Географические координаты

Для чего нужны географические координаты. Что значит определить географическую широту.

Для чего нужны географические координаты

Любая точка на земном шаре имеет свой географический адрес. Этот адрес состоит из двух частей. Когда вы играете в морской бой, то тоже используете «адрес» клеточки из двух частей — буквы и цифры. Две части географического адреса — широта и долгота. Определить их нам позволяет градусная сетка. Широта показывает место точки на определённой параллели, а долгота — место этой же точки на конкретном меридиане. Место их пересечения и есть нужный нам адрес — географические координаты.

Географические координаты любой точки на земном шаре — её широта и долгота.

Зная географические координаты, можно найти любой объект на карте и определить его положение по отношению к другим объектам.

И наоборот, можно нанести новый объект на карту, определив с помощью приборов его географические координаты, как это делали все первооткрыватели.

Уметь определять координаты по карте должен каждый человек. Для некоторых профессий это особенно важно, например для штурманов и военных. Штурманы прокладывают с помощью географических координат путь корабля, самолёта, подводной лодки. Иногда приходится искать в открытом океане терпящих кораблекрушение, а для этого необходимо знать место их нахождения. Геологи, геодезисты, географы, находясь в экспедиции, определяют координаты исследуемых ими объектов.

В настоящее время координаты на местности определяют с помощью прибора спутникового позиционирования (GPS — джи пи эс). Этот прибор определяет своё местоположение, получая информацию с нескольких искусственных спутников Земли. При перемещении объекта по местности на мониторе прибора вычерчивается траектория движения. Компьютерные программы для определения местонахождения любого объекта постоянно обновляют и совершенствуют. В повседневной жизни их разные версии закачивают на персональные компьютеры (например, Google Earth), мобильные телефоны и другие устройства.

ГЕОГРАФИЧЕСКИЕ КООРДИНАТЫ НЕОБХОДИМЫ ДЛЯ ТОЧНОГО ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ЛЮБОГО ОБЪЕКТА НА ЗЕМНОМ ШАРЕ.

Что значит определить географическую широту

Для всех точек, лежащих на одной и той же параллели, широта одинакова. Широта отсчитывается от экватора. Все точки, располагающиеся к северу от экватора, имеют северную широту (с. ш.), а располагающиеся к югу от экватора — южную широту (ю. ш.).

Россия, например, целиком лежит в Северном полушарии. Поэтому все географические объекты в нашей стране имеют северную широту. Наоборот, в Австралии, лежащей в Южном полушарии, широта везде южная.

Географическая широта — это расстояние в градусах от экватора до параллели, проведённой через заданную точку.

Северный тропик — это параллель 23,5° с. ш.

Южный тропик — это параллель 23,5° ю. ш.

Северный полярный круг — это параллель 66,5° с. ш.

Южный полярный круг — это параллель 66,5° ю. ш.

Для того чтобы узнать широту заданной точки, нужно найти параллель, на которой она расположена. Отсчёт начинаем от экватора, следуя строго вдоль меридиана на север или на юг (рис. 34). Все точки экватора имеют нулевую широту. Расстояние от экватора до полюса 90°. Чем больше мы будем удаляться от экватора, тем больше будет градусное расстояние до нужной нам параллели, тем больше будет её широта. Поэтому широты в полярных областях так и называются — высокие, а вблизи экватора — низкие.

Некоторые параллели специально подписывают и отмечают на картах. Это тропики и полярные круги.

Источник

Для чего нужны координаты?

Отец у меня был геодезистом, у него в кабинете висела карта мира, а на столе лежал маленький глобус. Я проводил большую часть своего времени, изучая их. Меня очень интересовали маленькие цифры, которые мне удалось обнаружить. Но только в школе я смог узнать, что это координаты.

Что такое координаты

Человечество ещё давным-давно научилось ориентироваться в пространстве. Это могли быть: мох, горы, леса и т. п. Они оставляли ориентиры: рисунки, обозначения. Потом появились карта, глобус, навигатор. Посмотрев на них, вы сразу увидите вертикальные и горизонтальные линии, что пересекаются и создают квадраты. Эти линии — параллели и меридианы. Каждый квадрат имеет долготу и широту. Для наглядности возьмите глобус.

Широта, долгота, глубина и высота — координаты, определяющие нахождение точки на Земле.

Координаты — числа, величины, что обозначают место положения объекта в пространстве.

Где используются координаты

Сегодня использование координат в повседневной жизни не имеют большого значения, навигатор сможет доставить в точку назначения без лишних усилий и знаний, но в других, более сложных областях, координаты играют великую роль.

Приведу лишь несколько примеров, так как их очень много, перечисление заберёт очень большое количество времени.

В топографии и геодезии координаты имеют широкое использование. С их помощью создаются топографические карты, вычисляется территория, измеряется ширина и длина местности.

В математике вычисляют размеры фигур. Векторы, гиперболы тоже имеют свои координаты — (x; y), которые нашли своё применение и в моделировании.

Виды координат

Поскольку координаты встречаются в разных областях, то их решили поделить на такие виды:

Моё знакомство с географическими координатами произошло ещё в школе. Правда, тогда мне казалось, что это абсолютно бесполезная информация. Но я очень сильно ошибался. Как-то раз я поехал на машине в путешествие. У автомобиля как назло лопнуло колесо. Указателей или близлежащих поселений там не было. Позвонив другу, я не смог даже примерно описать, где нахожусь. В той ситуации меня спас навигатор, а точнее точные географические координаты моего местоположения.

Для чего понадобились географические координаты

В повседневной жизни географические координаты, как правило, совершенно бесполезная вещь. Но отправляясь в поездку своим ходом, вы пользуетесь навигатором или картой. Очевидно, что карта появилась значительно раньше навигатора. Составляя карту, древние люди задавались вполне логичным вопросом. А как, глядя на карту, можно понять, в какую именно сторону нужно идти, чтобы попасть в определённое место? Без этой информации было бы невозможно покорять неизведанные края. Для решения проблемы было придумано разделить весь земной шар линиями, которые бы делили его на своеобразные квадратики. Таким образом, можно было понять, глядя на компас, в какую сторону двигаться. Правда, компас появился только в 13-м веке, а для определения сторон света, люди ориентировались по Солнцу.

Кому нужны географические координаты

Область применения географических координат достигает колоссальных размеров. Географические координаты используют:

Этот список очень большой. На перечисление всех видов деятельности, в которых используются географические координаты, элементарно не хватит времени.

Интересный факт о географических координатах

Оказывается, что не только на нашей планете есть широта и долгота. Астрономы позаботились и о других планетах нашей Солнечной системы. Они создали на тех планетах аналогичную систему координат, которая охватывает ещё и их сферы. Эта система координат потребовалась для различных астрономических исследований, а также активно применяется в космонавтике.

Как же часто я на уроках географии встречался с координатами. Также во многих играх мне приходилось их определять или просто наблюдать, как это делают герои. Поиск правильных координат также можно наблюдать и в фильмах. В общем, координаты являются очень важными, и необходимо знать про них, так как они могут пригодиться в реальной жизни.

Как в географии описываются координаты

Впервые каждый из нас узнал, что такое координаты, на уроках географии. Там мне ясно дали понять, что они нужны, чтобы не заблудиться в мире. С их помощью человек будет твердо знать, куда направляется и где находится на земном шаре в тот или иной момент. Чтобы их определить, необходимо уметь пользоваться картой или глобусом. На них, помимо материков, стран и городов, показаны цифры, которые особым образом располагаются по карте.

Расположение цифр выполняется по условным линиям. Их еще называют параллелями и медианами, которые показывают долготу и широту. Каждое место на планете имеет свою долготу и широту, которую можно определить по карте.

В географии Землю принято считать идеальной сферой, а не эллипсом. Сфера имеет угол в 360 градусов, поэтому на карте планета разделена на столько же условных линий. Планета крутится вокруг своей оси и имеет Северный и Южный полюса. Эти полюса указывают на долготу, и на планете существуют две важные такие линии. Одна называется нулевой, а вторая ─ 180 градусов.

Параллелями являются линии, которые показывают широту. Каждая линия широты расположена поперек вращения Земли вокруг своей оси. На экваторе располагается главная параллель, которая разделяет планету на 2 полушария, и в каждом насчитывается по 90 линий широты.

В географии градусы принято ещё делить на минуты и секунды.

Зачем нужны координаты

Мореплавателям приходится прибегать к помощи координат. Таким образом можно определить, где они находятся, чтобы выбрать правильный курс и не заблудится в морских или океанических водах.

Благодаря медианам и параллелям, наша планета для удобства поделена на следующие полушария:

Координаты в системе пространство-время

Евклидово пространство, которое плотно изучают в школе, не привязано ко времени, и там нет такого понятия как событие, а существует система неподвижных тел с тремя координатами:

В теории относительности же введено понятие времени, и оно как бы идет параллельно с другими координатами.

С введением времени в пространстве появляется место событию, которым может быть изменение, перемещение, исчезновение тела. Таким образом, исходя из общих законов физики, время ограничивает существование тела в пространстве до момента перехода его энергии в другое состояние. Ведь известно, что энергия никуда не исчезает, а лишь меняет свою форму.

Координаты «летящей стрелы»

Эта апория (безысходность) была предложена древнегреческим философом Зеноном. Заключается она в том, что летящая стрела будет неподвижна в каждый отрезок времени, соответственно, координаты ее меняться не будут, поэтому относительно временного отрезка она двигаться не будет.

Предположить же, что если взять более мелкие периоды времени, то стрела все же будет двигаться — невозможно, т. к. дробление времени может быть бесконечным, и, соответственно, в каждом более мелком периоде стрела имеет постоянные координаты и не движется. Загвоздка состоит в том, что в природе нет физического эквивалента математическим понятиям времени.

Координаты при перемещении во времени

Вопрос хорошо отражен в теории Уэллса в «Машине времени». Если перемещаться относительно шкалы времени, то координаты предмета должны быть неподвижны.

Сам же предмет должен быть защищен особым полем, которое будет разрушать внешние объекты, которые могут находится в тех же 3-мерных координатах при перемещении путешествующего предмета.

Любой человек в мире имеет какие-то свои признаки для ориентации во времени, пространстве и так далее. Одним из таких признаков являются координаты, с помощью которых люди могут знать точное местоположение и не только. Но я задался в свое время вопросом, что такое эти координаты в научном понимании и какие они бывают.

Координаты в географии

Широта, долгота и высота

Для точного и полного определения места нахождения той или иной точки, используются следующие три характеристики:

Применение координат в географии

Простыми словами из всего вышесказанного, географические координаты нужны для ориентации в пространстве или для навигации на какой-либо заданной местности. То есть, я могу знать координаты любого здания или города, или простого дерева, и тогда буду иметь возможность добраться до заданного места, имея навигатор.

Ответ на это вопрос для меня стал очевидным, когда я потерялся в таёжных лесах Сибири. Расскажу вам для чего нужны координаты, что это такое, и как я нашелся.

Необходимость координат

Координаты нужны для того, чтобы не потеряться или что-нибудь найти.

Координатами могут стать любые объекты или направления в пространстве. Например, мое место жительства – поселок Михайловский. Но такие поселки есть в каждой области России. Более точным будет указать область, например Московскую. Вы скажете: «В Московской области несколько таких поселков». Тогда нужно знать и район области. Например, Солнечногорский. Так, поселок вы уже нашли, но меня-то – нет. Меня нужно разыскать еще и в поселенке.

Область, район и поселок – это приблизительные, не точные координаты моего места пребывания. А вот знание географических координат поможет вам отыскать меня гораздо быстрее. Географические координаты указаны на полях любой мало-мальски точной карты региона и в современных телефонных устройствах, обрадованных системами навигации.

Географические координаты

Географические координаты – это числа, которые показывают ваше место в комнате, городе, стране или океане. Географические координаты определяются тремя параметрами:

…А нашелся я очень просто: сообщил о своих координатах в лагерь геологической экспедиции. Координаты я определил по топографической карте (они записываются на полях), согласно двух ориентиров – озера и поселения, к которым я поочередно вышел.

Источник

§ 2. Система географических координат

Вопрос 1. Что такое экватор?

Экватор – линия сечения земной поверхности плоскостью, проходящей через центр Земли, перпендикулярно оси ее вращения. Его длина приблизительно равна 40075 км. Экватор делит земной шар на Северное и Южное полушария.

Вопрос 2. На какие полушария экватор делит Землю?

Экватор делит земной шар на Северное и Южное полушария.

Вопрос 3. Какие планеты входят в состав Солнечной системы?

В состав Солнечной системы входят следующие планеты: ☿ Меркурий, ♀ Венера, ⊕ Земля, ♂ Марс, ♃ Юпитер, ♄ Сатурн, ♅ Уран, ♆ Нептун.

Вопрос 4. Можно ли одинаково определять координаты на плоскости и на поверхности шара?

Да, можно, для этого надо знать широту и долготу.

Вопрос 5. Для чего нужны координаты?

Для определения местоположения точки на карте или глобусе нужно знать две координаты.

Вопрос 6. На какие полушария экватор делит земной шар?

Экватор делит земной шар на Северное и Южное полушария.

Вопрос 7. Что такое параллель?

Линии, параллельные экватору, имеющие разную широту, называются параллелями. На географических картах параллели изображены в виде прямых линий или дуг окружностей разной кривизны, а на глобусе — в виде окружностей разного диаметра. Чем ближе к полюсу, тем диаметр окружности меньше.

Вопрос 8. Что такое меридиан?

Линия, соединяющая на поверхности Земли кратчайшим образом оба полюса, называется меридианом.

Вопрос 9. Почему начальный меридиан называют Гринвичским? Нулевым?

Потому что меридиан, который проходит через старую астрономическую обсерваторию, которая находилась в Англии в городке Гринвич, стали называть начальным, нулевым или Гринвичским.

Вопрос 10. На какие полушария делят земной шар нулевой и 180-й меридианы?

Если двигаться от Гринвичского меридиана на восток до меридиана 180°, то мы будем находиться в Восточном полушарии. Если, наоборот, на запад от Гринвичского меридиана, то до самого 180-го меридиана мы будем находиться в Западном полушарии.

Вопрос 11. Что показывает географическая широта?

Географической широтой точки называют выраженное в градусах расстояние от экватора до этой точки. Широта бывает северная и южная. Изменяется географическая широта от 0 до 90°. С помощью параллели определяется направление запад—восток.

Вопрос 12. Что такое географическая долгота?

Географической долготой точки называют выраженное в градусах расстояние от начального меридиана до этой точки. Долгота бывает восточная и западная.

Вопрос 13. В каких интервалах изменяются значения географической широты и географической долготы?

Географическая широта изменяется от 0 до 90°. Географическая долгота изменяется от 0° до 180°.

Вопрос 14. Чем экватор отличается от любой другой параллели?

Экватор является линией отсчёта географической широты, поэтому его собственная географическая широта — 0 ш. Экватор идет по центру и является самой большой по диаметру и радиусу параллелью.

Вопрос 15. Какие географические координаты имеют полюса Земли? Объясните отличие этих координат от координат любой другой точки на поверхности Земли.

Полюса имеют максимальное значение широты, равное 90°. Северный полюс — 90° с. ш., Южный — 90° ю. ш. Отличие от других координат заключается в том, что полюса не имеют значений долготы.

Вопрос 16. Почему отличается форма параллелей и меридианов на карте и глобусе?

Форма параллелей и меридианов отличается на карте и глобусе, т.к. глобус имеет форму шара — так же как и сама Земля, а карта — это изображение Земли на плоскости, поэтому есть искажения.

Вопрос 17. С использованием карт атласа определите географические координаты Москвы, Парижа и Сиднея. Что объединяет географические координаты: Москвы и Парижа; Москвы и Сиднея?

Москва: 55° с. ш. 37° в. д. Париж: 48° с. ш. 2° в. д. Сидней: 33° ю. ш. 151° в. д. Координаты Парижа и Москвы объединяет то, что эти города находятся в Северном и Западном полушариях, а Москву и Сидней то, что они находятся в Западном полушарии.

Вопрос 18. Определите географические координаты точки пересечения экватора и начального меридиана.

Географическая широта экватора — 0°. Географическая долгота начального — 0°. Следовательно, координаты точки пересечения 0° ш. 0° д.

Источник

География. 5 класс

Конспект урока

Урок 12. Географические координаты.

Перечень вопросов, рассматриваемых на уроке

Географические координаты, Географическая широта

Градусная сеть – это система меридианов и параллелей на географических картах и глобусах, служащая для отсчета географических координат точек земной поверхности (долгот и широт) или нанесения на карту объектов по их координатам.

Географические координаты – широта и долгота, определяют положение точки на земной поверхности

Географическая широта – это расстояние в градусах от экватора до параллели, проведённой через заданную точку.

Географическая долгота – расстояние от нулевого меридиана до заданной точки, выраженное в градусах.

Обязательная и дополнительная литература по теме

Теоретический материал для самостоятельного изучения

География – одна из древнейших наук, она тесно связана с жизнью человека. Очень часто в текстах песен, названиях фирм, компаний, торговых организаций используются географические термины и названия. Послушайте музыкальный фрагмент, что из области географии использовали авторы в тексте своей песни? Землю обмотали тоненькие нити,

Нити параллелей и зелёных рек.

Совершите чудо, руку протяните,

Надо, чтобы в дружбу верил каждый человек.

В песенке упоминаются параллели, уже известные нам линии на глобусе и карте.

Разбор типового тренировочного задания:

Тип задания: Выделение цветом;

Текст вопроса: По координатам определите город, расположенный на востоке от Владимира (56° с. ш. и 40,5° в. д.).

Великие Луки (56,5° с. ш. и 30,5° в. д.)

Вологда (59° с. ш. и 40° в. д.)

Казань (56° с. ш. и 49° в. д.)

Киров (58,5° с. ш. и 49,5° в. д.)

Правильный вариант ответа:

Казань (56° с. ш. и 49° в. д.)

Разбор типового контрольного задания

Тип задания: Подстановка элементов в пропуски в тексте

Текст вопроса: Заполните пропуски в тексте

1. Географическая широта – это расстояние в ________ от _______ экватора до _________, __________ через точку.

2. Географическая долгота – это расстояние в в ________ от _______ экватора до _________, __________ через точку.

Правильный вариант/варианты (или правильные комбинации вариантов):

Источник

Творческие проекты и работы учащихся

В процессе работы над индивидуальным проектом по математике «Координаты в нашей жизни» учеником 6 класса школы была поставлена и реализована цель, выяснить, где еще кроме математики применяется система координат. Для этого автор дает определение понятиям «координаты» и «система «координат», кратко излагает историю возникновения системы координат.

Подробнее о проекте:

В готовом творческом и исследовательском проекте по математике «Координаты в нашей жизни» автор выполняет практические задания, рассчитанные на построение изображений на координатной плоскости, а также изучает технологию расчета координатных данных для выполнения «рисунка» в прямоугольной системе координат. Предложенный детский проект позволяет научиться свободно ориентироваться на координатной плоскости и на географической карте.

Оглавление

Введение
1. Координаты. Системы координат.
1.1. История возникновения системы координат.
1.2. Координатная плоскость в математике.
1.3. Координаты вокруг нас.
1.4. Географические координаты.
2. Изображения на координатной плоскости.
2.1. Построение изображений на координатной плоскости.
2.2. Создание «рисунков» в прямоугольной системе координат.
Заключение
Приложение

Введение

Подробное изучение координатной плоскости необходимо. Ведь координаты- это тот же адрес. В повседневной жизни в речи взрослых мы иногда слышим такую фразу: “Оставьте мне свои координаты”. Это выражение означает, что собеседник должен оставить свой адрес или номер телефона, что и считается в этом случае координатами человека. Главное здесь в том, что по этим данным можно найти человека.

Именно в этом и состоит суть координат или, как обычно говорят, системы координат: это правило, по которому определяется положение того или иного объекта. Метод координат позволяет применять сред­ства алгебры и математического анализа при ре­шении геометрических задач. При работе с координатной плоскостью мы неоднократно можем менять расположение точек, размеры единичных отрезков, что требует высокого развития и логического мышления, и, следовательно, способствует его развитию.

В окружающем нас мире сущест­вует много явлений и объектов-прообразов, ко­торые можно использовать для составления зада­ний на метод координат. Если на уроках математики, каждой точке на числовой прямой ставилась в соответствии единственная координата (единственный адрес), то на уроках географии каждой точке на карте соответствуют уже два адреса, две координаты – долгота и широта.

Например, координаты Кемерово: 37,60 восточной долготы и 55,80 северной широты. В математике встречается следующую запись: А (3; 5) – точке А сопоставлены в соответствие два числа, два адреса, две координаты. Так, значит, существует взаимосвязь между математическими координатами и географическими координатами. Весьма интересный ма­териал предоставляет нам астрономия, где каждое созвездие тесно связанно с координатами.

Проблема: С координатами в геометрии мы сталкиваемся постоянно, а где еще применяется метод координат?

Цель: выяснить, где еще кроме математики применяется система координат.

История возникновения системы координат

Первоначальное применение координат конечно связано с астрономией и географией, с потребностью определять положение светил на небе и определенных пунктов на поверхности Земли, при составлении календаря, звездных и географических карт. Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта. Основная заслуга в создании современного метода координат принадлежит французскому математику Рене Декарту (см.приложение 1,рис.1).

До наших времён дошла такая история, которая подтолкнула его к открытию. Занимая в театре места, согласно купленным билетам, мы даже не подозреваем, кто и когда предложил ставший обычным в нашей жизни метод нумерации кресел по рядам и местам. Оказывается эта идея осенила знаменитого философа, математика и естествоиспытателя Рене Декарта (1596-1650)– того самого, чьим именем названы прямоугольные координаты.

Посещая парижские театры, он не уставал удивляться путанице, перебранкам, а подчас и вызовам на дуэль, вызываемыми отсутствием элементарного порядка распределения публики в зрительном зале. Предложенная им система нумерации, в которой каждое место получало номер ряда и порядковый номер от края, сразу сняла все поводы для раздоров и произвела настоящий фурор в парижском высшем обществе.

Научное описание прямоугольной системы координат Рене Декарт впервые сделал в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Кроме того, в своей работе «Геометрия» (1637), открывшей взаимопроникновение алгебры и геометрии, Декарт ввел впервые понятия переменной величины и функции. «Геометрия» оказала огромное влияние на развитие математики. В декартовой системе координат получили реальное истолкование отрицательные числа.

Кроме математики интересы Декарта распространялись на физику, где он дал четкую формулировку закона инерции, открыл закон преломления световых лучей на границе двух различных сред («Диоптрика», 1637).

Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.

Координатная плоскость в математике

Каж­дый объ­ект имеет свой упо­ря­до­чен­ный адрес (ко­ор­ди­на­ты). Таким об­ра­зом, адрес или ко­ор­ди­на­ты – это чис­ло­вое или бук­вен­ное обо­зна­че­ние того места, где на­хо­дит­ся объ­ект.

Ма­те­ма­ти­ка­ми была раз­ра­бо­та­на мо­дель, ко­то­рая, в част­но­сти, поз­во­ля­ет опи­сать любой зри­тель­ный зал (рас­по­ло­же­ние мест в зале). Такая мо­дель по­лу­чи­ла на­зва­ние ко­ор­ди­нат­ная плос­кость.

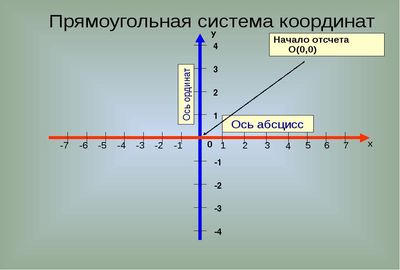
Чтобы из обыч­ной плос­ко­сти по­лу­чить ко­ор­ди­нат­ную, необ­хо­ди­мо на­чер­тить две пер­пен­ди­ку­ляр­ные пря­мые, от­ме­чая стрел­ка­ми на­прав­ле­ния «впра­во» и «вверх». На пря­мые на­но­сят де­ле­ния, как на ли­ней­ку, при­чем точка пе­ре­се­че­ния пря­мых – это ну­ле­вая от­мет­ка для обеих шкал. Го­ри­зон­таль­ную пря­мую обо­зна­ча­ют Х и на­зы­ва­ют осью абс­цисс, вер­ти­каль­ную пря­мую обо­зна­ча­ют У и на­зы­ва­ют осью ор­ди­нат.

Две пер­пен­ди­ку­ляр­ные оси Х и У с раз­мет­кой на­зы­ва­ют пря­мо­уголь­ной, или де­кар­то­вой, си­сте­мой ко­ор­ди­нат. На­зва­ние «де­кар­то­ва» про­ис­хо­дит от фа­ми­лии фран­цуз­ско­го фи­ло­со­фа и ма­те­ма­ти­ка Рене Де­кар­та, ко­то­рый ее при­ду­мал (см.приложение 1,рис. 2).

Для любой точки на ко­ор­ди­нат­ной плос­ко­сти можно ука­зать два числа (ко­ор­ди­на­ты). На ри­сун­ке по­ка­за­на точка на ко­ор­ди­нат­ной плос­ко­сти. Для по­лу­че­ния ко­ор­ди­нат этой точки необ­хо­ди­мо через точку про­ве­сти две пря­мые, па­рал­лель­ные ко­ор­ди­нат­ным осям (обо­зна­че­ны пунк­тир­ной ли­ни­ей). Пе­ре­се­че­ние одной из пря­мых с осью абс­цисс – это ко­ор­ди­на­та точки, пе­ре­се­че­ние дру­гой пря­мой с осью ор­ди­нат – это ко­ор­ди­на­та точки. Сна­ча­ла ука­зы­ва­ют ко­ор­ди­на­ту, потом. Точка имеет ко­ор­ди­на­ты. Ана­ло­гич­но на­хо­дим ко­ор­ди­на­ты точки, она имеет ко­ор­ди­на­ты.

Координаты вокруг нас

Системы координат пронизывают всю практическую жизнь человека. В нашей речи вы не раз могли слышать такую фразу: «Оставьте мне ваши координаты». Что означает это выражение? Догадались?! Собеседник просит записать свой адрес или номер телефона. У каждого человека бывают ситуации, когда необходимо определить местонахождение: по билету найдите место в зрительном зале или в вагоне поезда.

Координаты окружают нас повсюду:

Географические координаты

При попадании в аварийную ситуацию, человек первым делом должен уметь ориентироваться на местности. Иногда необходимо определить географические координаты своего местоположения, например, чтобы передать спасательной службе или для других целей.

В современной навигации стандартно используется всемирная система координат WGS-84. В этой системе координат работают все GPS навигаторы и основные картографические проекты в Интернете. Координаты в системе WGS-84 столь же общеупотребимы и понятны всем, как всемирное время.

Местоположение любого объекта на поверхности Земли, его «адрес», определяется географической широтой («адрес» по горизонтали) и географической долготой («ад­рес» по вертикали). Широта и долгота — это географиче­ские координаты точки земной поверхности

Географическая широта заданной точки определяется величиной в градусах дуги меридиана от экватора до параллели, проходящей у точку.

Географическая долгота. Долгота отсчитывается в градусах вдоль параллели. Началом отсчета долгот условно вы­бран Гринвичский (нулевой, начальный) меридиан, который про­ходит через старую Гринвичскую обсерваторию в Лондоне. На­чальный меридиан и меридиан 180° разделяют Землю на Восточное и Западное полушария.

Все точки Восточного полушария имеют вос­точную долготу (в. д.), а Западного — западную долготу (з. д.). Как восточная, так и западная долгота отсчитываются от 0 до 180°. Циф­ры, обозначающие градусы долготы, написаны на глобусе и на кар­те полушарий у точек пересечения меридианов с экватором. Географическая долгота заданной точки определяется величиной в градусах дуги параллели от начального меридиана до меридиана, проходящего через эту точку.

Построение изображений на координатной плоскости

У древних греков существовала легенда о созвездиях Большой Медведицы и Малой Медведицы:«Всемогущий бог Зевс решил взять себе в жены прекрасную нимфу Калисто, одну из служанок богини Афродиты, вопреки желанию последней. Чтобы избавить Калисто от преследований богини, Зевс обратил Калисто в Большую Медведицу, а ее любимую собаку – в Малую Медведицу и взял их на небо».

Существует множество легенд и мифов о созвездиях. Фантазия древних греков поместила их на небо. Так появились созвездия Цефея, Андромеды, Персея и т.д. Знакомство с координатной плоскостью и вид звездного неба натолкнули на мысль, о переносе некоторых созвездий на координатную плоскость.

Созвездие Лев. В этом созвездии запечатлен Немейский Лев, над которым одержал победу Геракл.

Созвездие Близнецы. Созвездие названо в честь двух неразлучных братьев, сыновей Елены Прекрасной – Кастора и Полидевка..

Большая Медведица. Согласно греческому мифу это созвездие олицетворяет прекрасную нимфу Каллисто, превращенную Зевсом в Медведицу, чтобы спасти её от мести Геры.

Малая Медведица. Созвездие известно как Малый Ковш, последняя звезда в «ручке» которого – Полярная.

Орион. В греческой мифологии Орион – сын Посейдона и Эвриалы, великий охотник.

Телец. Созвездие названо в честь быка, на котором Европа переплыла море и попала к Зевсу на Крит.

Создание «рисунков» в прямоугольной системе координат

На координатной плоскости интересно строить рисунки, используя построение графов по координатам. Нужно сначала нарисовать рисунок, а затем его перенести на координатную плоскость, но при этом плавные соединения должны быть в виде отрезков.

Заключение

В результате проведения исследования я доказал, что координатная плоскость используется не только в математике, а пронизывает всю практическую жизнь человека.

В настоящее время координатный метод широко применяется в повседневной жизни. Современные системы спутниковой навигации позволяют определять координаты объекта, а также следить и управлять объектами, в том числе и движущимися. Эта тема также представляет сегодня большой интерес и может стать темой новой исследовательской разработки в будущем.

Приложение

Карточка № 1. Рисуем по координатам

Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).

Карточка № 2. Рисуем по координатам

Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).

Карточка № 3. Рисуем по координатам

Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).

Карточка № 4. Рисуем по координатам

Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).

Ответы: 1 – утенок; 2 – заяц; 3 – белка; 4 – кошка.

Источник