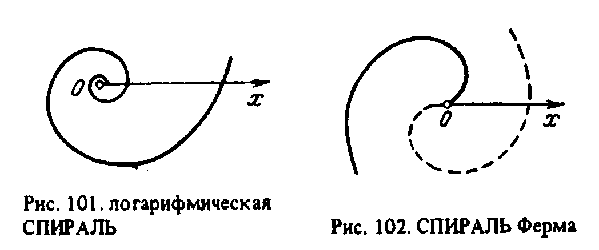Для чего нужны логарифмы в жизни
Для чего нужны логарифмы в жизни
Изучение темы «Логарифмы» начинается с определения:
Логарифмом положительного числа b по основанию a, где a > 0, a ≠ 1, называется показатель степени, в которую надо возвести число a, чтобы получить число b.
Обычно, такая первая встреча с логарифмами не вызывает у учеников особой радости и энтузиазма, логарифм невольно ассоциируется с чем-то трудным. Многие ворчат: «Ну, кому понадобились эти логарифмы?».
Я тоже задумался над этим и решил узнать мнения людей, окончивших школу, по этому вопросу. Результаты меня озадачили: из 20 опрошенных 15 (75%) считают, что логарифмы не нужно изучать. Так может быть они действительно не нужны? Меня очень заинтересовала эта проблема.
Предмет исследования – частные вопросы создания и применения логарифмов.
Проблема: логарифмы – прихоть математиков или жизненная необходимость?
Гипотеза: логарифмы нужны современному человеку.
Существует связь между звездами, шумом, музыкой, природой и логарифмами.
Цель работы – доказать необходимость изучения логарифмов.
Для достижения своей цели, я выдвинул следующие задачи:
найти, собрать и проанализировать материал по истории возникновения логарифмов;
проанализировать, где в природе встречаются логарифмы;
проанализировать, в каких сферах жизнедеятельности человека применяются логарифмы;
сделать соответствующие выводы по исследовательской работе.
При проведении исследования были использованы следующие методы исследования:
анализ существующей литературы по рассматриваемой проблеме (метод научного анализа).
обобщение и синтез точек зрения, представленных в литературе (метод научного синтеза и обобщения).
моделирование на основе полученных данных авторского видения в раскрытии поставленной проблемы (метод моделирования).
2.1. История возникновения и развития логарифмов
Изобретение логарифмов, сократив
работу астронома, продлило ему жизнь.
Испокон веков люди пытались упростить вычисления: составляли таблицы, вводили приближенные формулы, облегчающие расчеты, пытались заменить сложные операции умножения и деления более простыми – сложением и вычитанием.
Логарифмы также были созданы в 16 веке как средство для упрощения вычислений. В их основе лежит очень простая идея, знакомство с которой приписывается еще Архимеду.
Рассмотрим две прогрессии, арифметическую и геометрическую при b1 = 2, q = 2
1 2 3 4 5 6 7 8 9 10 (*)
2 4 8 16 32 64 128 256 512 1024
Но это еще не все. С помощью указанных двух строк (*) действие возведения в степень заменяется умножением, а извлечение корня – делением.
Идея Архимеда получила развитие не сразу. Пока математикам было достаточно уже имевшихся средств вычислений, они проходили мимо этого удивительного свойства прогрессий. Но в эпоху Возрождения ситуация изменилась. Крупнейшие европейские державы стремились к владычеству на море. Для дальних плаваний, для определения положения морских судов по звездам и по солнцу необходимо было всё более развивать астрономию, а значит, и тригонометрию. И, в частности, понадобились более совершенные тригонометрические таблицы. В связи с нарастающими запросами практики продолжали совершенствоваться астрономические инструменты, увеличивалась точность наблюдений, исследовались планетные движения. Обработка полученных данных требовала колоссальных расчетов, и, следовательно, стали необходимы новые средства упрощения вычислений. Такими средствами в 15 – 16 веках явились в первую очередь логарифмы и десятичные дроби.
Рассмотрим, как развивалась дальше идея логарифмов.
Прежде всего, теоретическая подготовка учения о логарифмах тесно связана с развитием понятия степени. Степень с отрицательным показателем встречается уже в трактате «Арифметика» древнегреческого математика Диофанта (ок. 3 в.) из Александрии. Им, а возможно и его предшественниками, были введены особые обозначения для некоторых положительных и отрицательных степеней. С течением времени символика совершенствовалась, и эта идея получила дальнейшее развитие. Так, много позже, французский врач и математик Никола Шюке (ок. 1445 – 1500) в своем трактате «Наука о числе» более полно рассмотрел нулевые и отрицательные показатели степени. Ещё раньше, в 14 веке, епископ города Лизье в Нормандии Николай Орем (ок. 1323 – 1382), исходя из соображений о возможности вставлять в арифметическом ряду между натуральными числами дробные, высказал мысль о том, как надо выражать в рядах (*) соответствующие величины геометрического ряда. Таким образом, он пришел к степеням с дробным показателем.
Особое внимание сопоставлению арифметического и геометрического рядов уделял Михаэль Штифель (1487 – 1567). Подобно Шюке и Орему Штифель пришел к мысли о дробных показателях. Кроме того, сопоставляя ряд натуральных чисел, начинающихся единицей, он отмечал, что соответствующий единице показатель есть нуль, т.е. что a 0 = 1. Числам верхнего ряда Штифель дал употребительное и поныне название «показателей» (exponent).
Но, кто же стал автором первых таблиц логарифмов, позволяющих свести более сложные действия к более простым?
В истории науки иногда наступают моменты, когда необходимость некоторого открытия осознается многими, а его основная идея как бы витает в воздухе. В таких случаях к открытию приходят не один, а сразу несколько ученых. Так случилось и в истории логарифмов. Однако создатели первых логарифмических таблиц подходили к изобретению нового удобного средства для упрощения вычислений по-разному. Те соображения, которые мы выдвинули чуть раньше, пытаясь предугадать, каким путем пойдет создатель логарифмов, пожалуй, больше всего подходят к Бюрги.
Таблицы Иоста Бюрги были ещё очень несовершенны, правила работы с ними достаточно трудоемки, а многие результаты приходилось находить с помощью дополнительных приближенных приемов вычислений.
Бюрги очень медлил с опубликованием своих таблиц. Они вышли в свет лишь в 1620 году под названием «Таблицы арифметической и геометрической прогрессий, вместе с основательным наставлением, как их нужно понимать и с пользой применять во всяческих вычислениях». Но значительного распространения эти таблицы не получили, так как к моменту опубликования таблиц Бюрги ученому миру уже семь лет были известны другие таблицы, которые составил шотландский барон Джон Непер (1550 – 1617).
Интересно, что наряду с вышеуказанными таблицами существовали ещё одни таблицы, которыми можно было пользоваться как средством для упрощения вычислений. Однако их автор не заметил этого, подразумевая совсем иное назначение своих таблиц. Речь идет о таблицах процентов шотландского ученого и инженера Симона Стевина (1548 – 1620).
Итак, можно заметить, что в один смысловой блок собираются такие понятия, как арифметическая и геометрическая прогрессии, степень, проценты, формула сложных процентов и логарифмы.
2.2. Применение логарифмов для познания окружающего мира
Если в 16 веке логарифмы появились как средство для упрощения вычислений, то нужны ли они сегодня, когда вычислительная техника достаточно развита, чтобы справляться с самыми сложными расчетами? Вопрос правомерен. Ведь не изучают же в современной школе такие старые средства для упрощения вычислений, как простейшие счетные приборы, не изучаются древние алгоритмы умножения и деления чисел, извлечения квадратных и кубических корней и прочее. Так зачем изучают логарифмы сегодня? Попробуем ответить на этот интересный вопрос.
Во-первых, логарифмы и сегодня позволяют упрощать вычисления.
Во-вторых, испокон веков целью математической науки было помочь людям узнать больше об окружающем мире, познать его закономерности и тайны.
Ряд явлений природы помогает описать логарифмическая зависимость. Иначе говоря, математики, пытаясь составить математическую модель того или иного явления, достаточно часто обращаются именно к логарифмической функции.
Одним из наиболее наглядных примеров такого обращения является логарифмическая спираль. (см. Приложение 1.) Спираль в одну сторону развертывается до бесконечности, а вокруг полюса, напротив, закручивается, стремясь к нему, но не достигая.
a ) Логарифмическая спираль в природе.
Так почему в качестве примера логарифмической зависимости в природе выбирают именно логарифмическую спираль?
Немецкий биолог Румблер в 1910 году выдвинул теорию постоянного краевого угла при построении раковин улиток. Он исходил из того, что материал, из которого строятся раковины, вначале должен быть жидким, и в жидком состоянии попадает на край уже существующей части раковины где, естественно, всегда образуется постоянный краевой угол. Под этим углом жидкость затвердевает, и снова начинается та же игра. Раковина улитки представляет собой логарифмическую спираль.
Но не только раковины многих моллюсков, улиток, а даже рога таких млекопитающих, как архары (горные козлы), закручены по логарифмической спирали (см. Приложение 3.)
Можно сказать, что эта спираль является математическим символом соотношения формы и роста. Великий немецкий поэт Иоганн-Вольфганг Гёте считал её даже математическим символом жизни и духовного развития.
По логарифмической спирали очерчены не только раковины, но и в подсолнухе семечки (см. Приложение 4) расположены по дугам, близким к логарифмической спирали и т. д. Один из наиболее распространённых пауков – эпейра, сплетает нити паутины вокруг центра по логарифмическим спиралям (см. Приложение 5).
b ) Звёзды, шум и логарифмы.
Известно, что астрономы распределяют звезды по степеням видимой яркости на светила первой величины, второй величины, третьей и т.д. Последовательные звездные величины воспринимаются глазом как члены арифметической прогрессии. Но физическая яркость их изменяется по иному закону: объективные яркости составляют геометрическую прогрессию со знаменателем 2,5. Получается, что «величина» звезды представляет собой не что иное, как логарифм её физической яркости. Оценивая видимую яркость звёзд, астроном оперирует с таблицей логарифмов по основанию 2,5.
Рассмотрим несколько примеров. Тихий шелест листьев оценивается в 1 бел, громкая разговорная речь – в 6,5 бел, рычание льва – в 8,7 бела. Отсюда следует, что по силе звука разговорная речь превышает шелест листьев в раз; львиное рычание сильнее громкой разговорной речи в раз.
Случайность ли то, что и при оценке видимой яркости светил и при измерении громкости шума мы имеем дело с логарифмической зависимостью между величиной ощущения и порождающего его раздражения? Нет, и то, и другое – следствие общего закона (называемого «психофизическим законом Фехнера»), гласящего: величина ощущения пропорциональна логарифму величины раздражения. Как видим, логарифмы вторгаются и в область психологии.
c ) Логарифмическая спираль в технике.
Логарифмическая спираль знаменита не только тем, что её образы достаточно широко встречаются в природе, но и своими удивительными свойствами.
В технике часто применяют вращающиеся ножи. Сила, с которой они давят на разрезаемый материал, зависит от угла резания, т.е. угла между лезвием ножа и направлением скорости вращения. Для постоянства давления нужно, чтобы угол резания сохранял постоянное значение, а это будет в том случае, если лезвия ножей очерчены по дуге логарифмической спирали (см. Приложение 7).Величина угла резания зависит от обрабатываемого материала.
В гидротехнике по логарифмической спирали изгибают трубу, подводящую поток воды к лопастям турбины (см. Приложение 7). Благодаря такой форме трубы потери энергии на изменение и направление течения в трубе оказываются минимальными и напор воды используется с максимальной производительностью.
Пропорциональность длины дуги спирали радиус-вектору используют при проектировании зубчатых колёс с переменным передаточным числом. И через середину и конец каждой стороны проводят дуги одинаковых логарифмических спиралей (см. Приложение 7) с полюсами в центрах квадратов, причем одна спираль закручивается по часовой стрелке, а другая – против часовой стрелки. Тогда при вращении этих квадратов дуги спиралей будут катиться одна по другой без скольжения. Передаточное же число, т.е. отношение угловых скоростей этих колёс, будет непрерывно меняться, достигая в течение одного оборота колеса четыре раза максимального значения и четыре раза минимального.
d) Логарифмы и музыка.
«Даже изящные искусства питаются ею.
Разве музыкальная гамма не есть
Набор передовых логарифмов?»
И действительно, так называемые ступени темперированной хроматической гаммы (12-звуковой) частот звуковых колебаний представляют собой логарифмы. Только основание этих логарифмов равно 2 (а не 10, как принято в других случаях).
Логарифмируя эту формулу, получаем
lg = lg n + m lg 2 + + p ( lg 2)/12,
lg = lg n + (m + p/12)lg2.
Принимая частоту самого низкого “до” за единицу (n = 1) и приводя все логарифмы к основанию 2. имеем
e ) Логарифмы в разных отраслях науки
Логарифмы – это математическое понятие, которое применяется во всех отраслях науки: химии, биологии, физике, механике, информатике, электротехнике, географии и многих других.
Статистика постоянно использует понятие среднего. Средняя численность населения, средний уровень инфляции, средняя заработная плата и т.д. Для нахождения средних величин существует коэффициент усреднения он равен ln=2.
Сведения, собранные мною в данной работе, — это далеко не всё, что можно рассказать о логарифмах. В заключении обратимся еще раз к основной идее. Мы, обучаясь в школе, не просто впитываем некоторый набор информации. Мы усваиваем научные данные об окружающем мире, о его устройстве и законах. В этот период складывается картина мира, и чем полнее и объективнее она будет, тем лучше мы будем понимать и оценивать окружающую нас жизнь, тем более полноценными людьми будем себя ощущать. Поэтому стоит изучать вопросы, без которых картина мира будет неполноценной. С моей точки зрения, изобретение логарифмов по возможности можно смело поставить рядом с другими, более древним великим изобретением индусов – нашей десятичной системы счисления.
Результаты моего исследования следующие:
В ходе проведения исследовательской работы я нашел подтверждение словам Галилео Галилея «Великая книга природы написана математическими символами»;
Многие природные явления не могли быть изучены без понятия логарифма;
Логарифмы используются для описания природных явлений астрономами, физиками, биологами;
Понятие логарифма широко применяется человеком во многих науках.
Логарифм является инструментом для вычисления радиоактивного распада, изменения количества людей в стране, зависимости скорости ракеты от ее массы, коэффициента звукоизоляции.
Выяснил, что, играя по клавишам современного рояля, музыкант играет, собственно говоря, на логарифмах.
Материалы исследования имеют практическую значимость и могут быть использованы для дальнейшего изучения данной, столь увлекательной, на мой взгляд, темы.
Гипотеза моего исследования, что логарифмы нужны современному человеку, действительно подтвердилась.
Я постарался проследить, как в ходе истории возникала необходимость введения и изучения логарифмов, усиливалась их значимость. Показал применение логарифмов в современном мире. Тем самым, я смог доказать, насколько важно изучать логарифмы для познания окружающего мира.
Алимов Ш.А. Алгебра и начала анализа.- М.:Просвещение,2016.
Большая электронная энциклопедия «Кирилл и Мефодий»: 2004
Виленкин Н.Я. Алгебра и математический анализ.- М.:Мнемозина,2017.
Колмогоров А.Н. Алгебра и начала анализа.- М.:Просвещение,2016.
Лиман М.М. Школьникам о математике и математиках.- М.:Просвещение,1981.
Самсонов П.И. «Математика»:«Полный курс логарифмов. Естественнонаучный профиль». «Школьная пресса», М.2005
Энциклопедия для детей. Т. 11. Математика. – М.: Аванта+, 1998.
Приложение 1. Логарифмическая спираль.
Приложение 2. Раковины многих моллюсков, улиток закручены по логарифмической спирали.
Приложение 3. Рога таких млекопитающих, как архары (горные козлы), закручены по логарифмической спирали.
Приложение 4. В подсолнухе семечки расположены по дугам, близким к логарифмической спирали.
Приложение 5. Паук – эпейр сплетает нити паутины вокруг центра по логарифмическим спиралям.
Приложение 6. По логарифмическим спиралям также закручены и многие галактики, в частности Галактика, которой принадлежит Солнечная система.
Приложение 7. Лезвия вращающихся ножей очерчены по дуге логарифмической спирали. В гидротехнике по логарифмической спирали изгибают трубу, подводящую поток воды к лопастям турбины.
Старт в науке
Учредителями Конкурса являются Международная ассоциация учёных, преподавателей и специалистов – Российская Академия Естествознания, редакция научного журнала «Международный школьный научный вестник», редакция журнала «Старт в науке».
Логарифмы вокруг нас (работы моих учеников)
Цель: исследовать в каких областях науки, техники нашли применение логарифмы, логарифмическая функция.
Просмотр содержимого документа
«Логарифмы вокруг нас (работы моих учеников)»
Логарифмы вокруг нас Пустынникова Ирина
На протяжении 16 века быстро возрастало количество приближенных вычислений, прежде всего, в астрономии. Совершенствование инструментов, исследование планетных движений и другие работы потребовали колоссальных, иногда многолетних, расчетов. Астрономам грозила реальная опасность утонуть в невыполненных расчетах.
Логарифмы были изобретены шотландским математиком Джоном Непером (1550–1617) в 1614 г. Его «Канон о логарифмах» начинался так: «Осознав, что в математике нет ничего более, скучного и утомительного, чем умножение, деление, извлечение квадратных и кубических корней, и что названные операции являются бесполезной тратой времени и неиссякаемым источником неуловимых ошибок, я решил найти простое и надежное средство, чтобы избавиться от них».
С точки зрения вычислительной практики, изобретение логарифмов по возможности можно смело поставить рядом с другими, более древним великим изобретением индусов – нашей десятичной системы нумерации.
Через десяток лет после появления логарифмов Непера английский ученый Гунтер изобрел очень популярный прежде счетный прибор – логарифмическую линейку. Она помогала астрономам и инженерам при вычислениях, она позволяла быстро получать ответ с достаточной точностью в три значащие цифры.
Таким образом, потребность в сложных расчётах быстро росла. Теория логарифмов связана с именами целого ряда математиков: Генри Бригс, Эдмунд Уингейт, Уильям Отред, Н. Меркатор, Джон Спейдел, К. Бремикер, Ф. Клейн.
Анализ тематики создание логарифмов достаточно актуален и представляет научный и практический интерес.
Цель: исследовать в каких областях науки, техники нашли применение логарифмы, логарифмическая функция.
Задача: 1. Актуализация практической значимости математических знаний;
2. Развитие нравственных представлений о природе математики, сущности и происхождении математической абстракции.
Проблема: показать практическую значимость логарифмов для окружения.
Логарифмы были изобретены не позднее 1594 года независимо друг от друга шотландским бароном Непером (1550-1617) и через десять лет швейцарским механиком Бюрги (1552-1632). Оба хотели дать новое удобное средство арифметических вычислений, хотя подошли они к этой задаче по-разному. Непер кинематически выразил логарифмическую функцию и, тем самым, вступил в новую область теории функции. Бюрги остался на почве рассмотрения дискретных прогрессий. Впрочем, определение логарифма у обоих не похоже на современное.
В ходе тригонометрических расчётов, Неперу пришла в голову идея: заменить трудоёмкое умножение на простое, сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной.
В 1614 году Непер опубликовал в Эдинбурге сочинение под названием «Описание удивительной таблицы логарифмов», на латинском языке. Там было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов.
Сочинение было разделено на 2 книги, из которых первая посвящена логарифмам, а вторая — плоской и сферической тригонометрии, причём вторая часть одновременно служит практическим пособием по первой. Более развёрнутое, описание содержалось в другом труде, изданном посмертно его сыном; там же Непер пояснил, как он составлял свои таблицы.
Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом.
К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.
Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Вега́ появилось только в 1857 году в Берлине (таблицы Бремивера).
В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.
Знаки log и Log были введены в 1624 году И. Кеплером.
Термин «натуральный логарифм» ввели Менголи в 1659 г. и вслед за ним Н. Меркатор в 1668 г., а издал таблицы натуральных логарифмов чисел от 1 до 1000 под названием «Новые логарифмы» лондонский учитель Джон Спейдел.
На русском языке первые логарифмические таблицы были изданы в 1703 году. Но во всех логарифмических таблицах были допущены ошибки при вычислении. Первые безошибочные таблицы вышли в 1857 году в Берлине в обработке немецкого математика К. Бремикера (1804-1877).
Дальнейшее развитие теории логарифмов связано с более широким применением аналитической геометрии и исчисления бесконечно малых. К тому времени относится установление связи между квадратурой равносторонней гиперболы и натуральным логарифмом.
С открытием логарифмического ряда изменилась техника вычисления логарифмов: они стали определяться с помощью бесконечных рядов.
В своих лекциях «Элементарная математика с высшей точки зрения», прочитанных в 1907-1908 годах, Ф. Клейн предложил использовать формулу в качестве исходного пункта построения теории логарифмов.
Таким образом, прошло 394 года с тех пор, как логарифмы впервые были введены (считая с 1614 г.), прежде чем математики пришли к определению понятия логарифма, которое положено теперь в основу школьного курса.
Если вычислительные потребности практической жизни и технического обихода вполне обеспечиваются трех и четырехзначными таблицами то с другой стороны, к услугам теоретического исследователя имеются таблицы и с гораздо большим числом знаков, чем даже 14- значные логарифмы. Вообще говоря, логарифм в большинстве случаев есть число иррациональное и не может быть точно выражен никаким числом цифр; логарифмы большинства чисел, сколько бы знаков ни брать, выражаются лишь приближенно, тем точней, чем больше цифр в их мантиссе. Для научных работ оказывается иногда недостаточной точность 14- значных логарифмов, но среди пятисот всевозможных образов логарифмических таблиц вышедших в свет, со времени их изобретения, исследователь всегда найдет такие, которые его удовлетворяют. Например, 20- значные логарифмы чисел от 2 до1200, изданные во Франции Кале.
Рога козлов, раковина улитки и семечки в подсолнухе закручены по логарифмической спирали
Применение логарифмов в различных сферах жизнедеятельности человека
Народонаселение. Изменение количества людей в стране на небольшом отрезке времени с хорошей точностью описывается формулой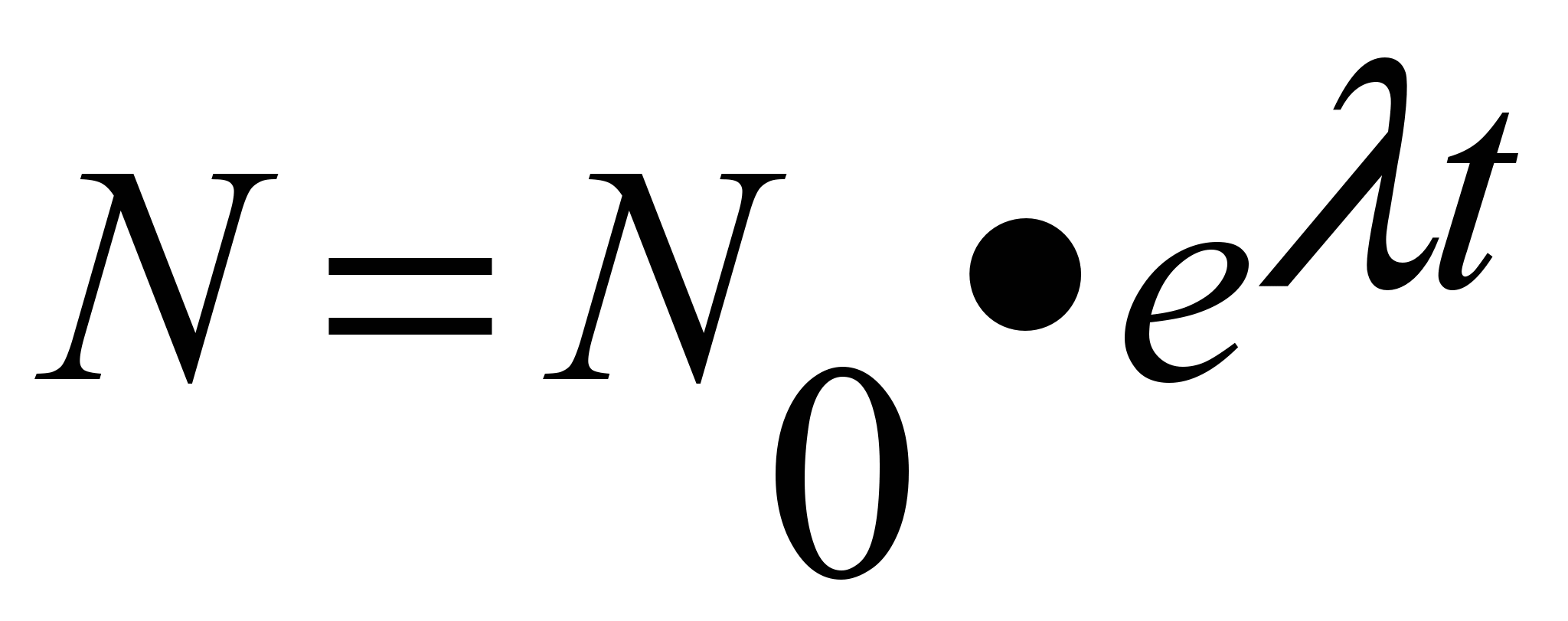 
, где N0 – число людей при t=0, N – число людей в момент t, λ – некоторая константа.
Звукоизоляция стен. Коэффициент звукоизоляции стен измеряется по формуле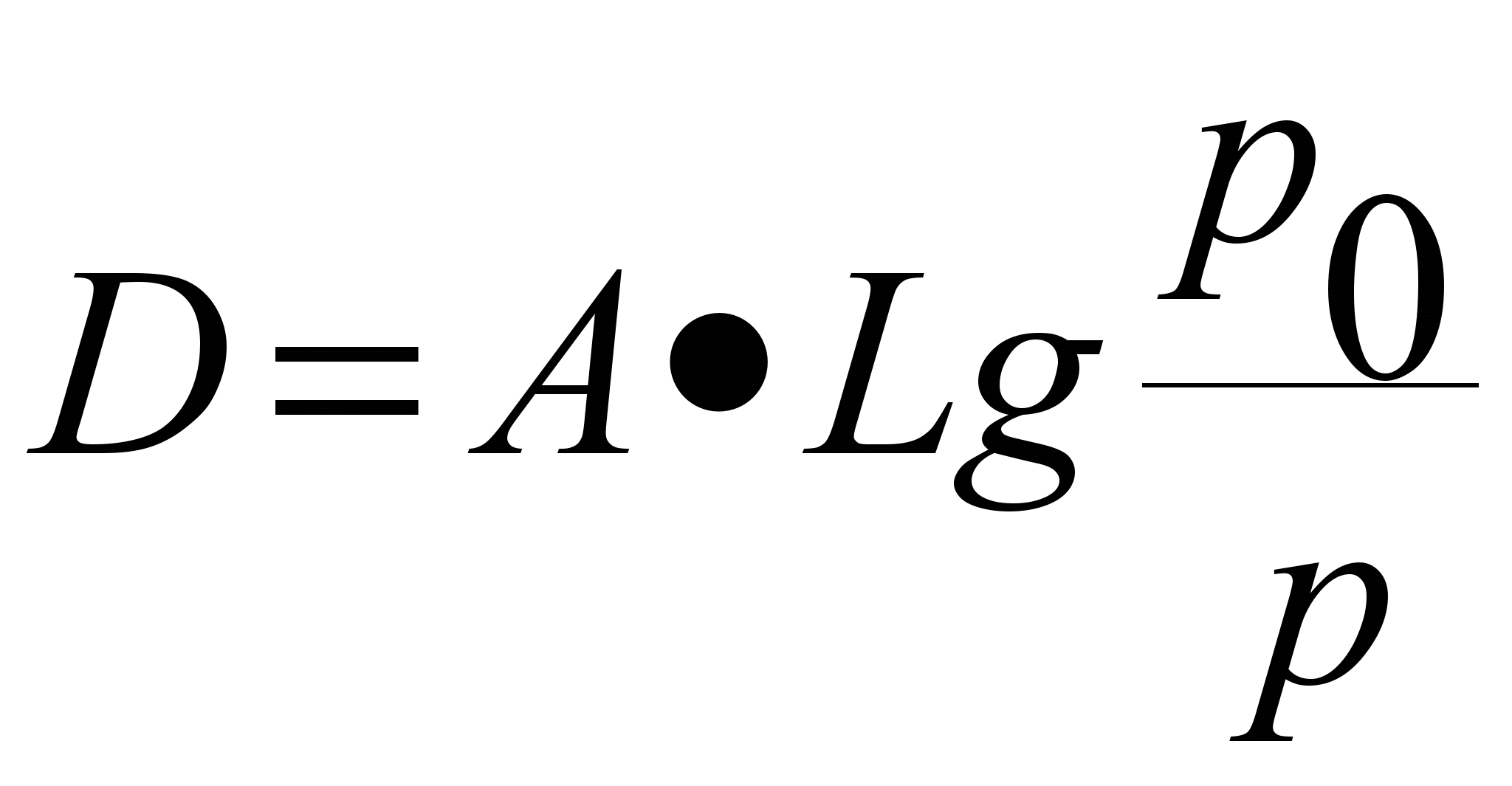
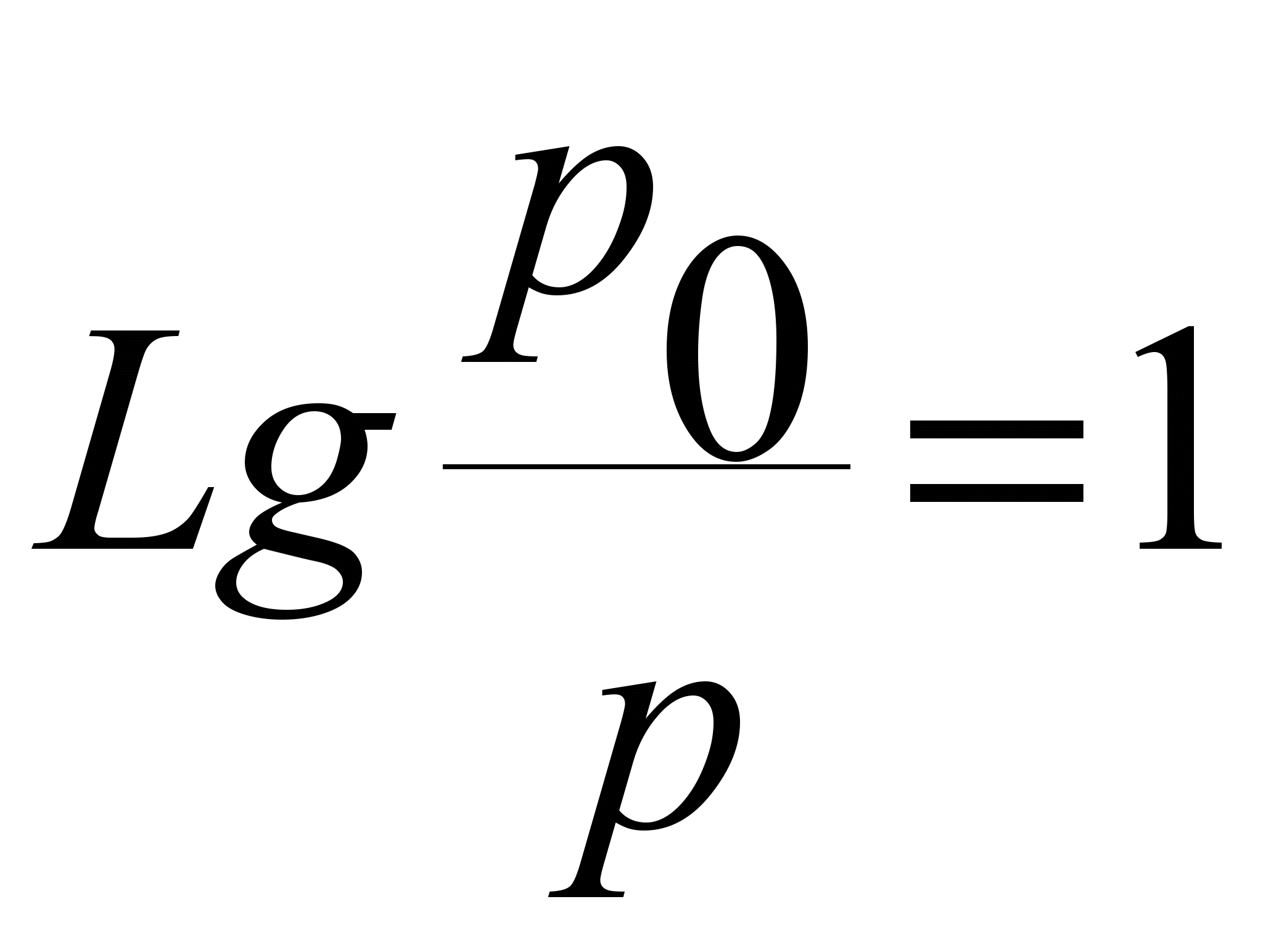
, где p0 – давление звука до поглощения, p – давление звука, прошедшего через стену, А – некоторая константа, которая в расчетах принимается равной 20 децибелам. Если коэффициент звукоизоляции D равен, например 20 децибел, то это означает, 
что и p0 =10p, т.е. стена снижает давление звука в 10 раз. Такую изоляцию имеет деревянная дверь.
Логарифмы в музыке.
Играя по клавишам современного рояля, музыкант играет, собственно говоря, на логарифмах. И действительно так называемые «ступени» темперированной хроматической гаммы не расставлены на равных расстояниях ни по отношении к числам колебаний, ни по отношению к длинам волн соответствующих звуков, а представляют собой логарифмы этих величин. Основание этих логарифмов равно 2.
Номера клавишей рояля представляют собой логарифмы чисел – колебаний соответствующих звуков (умноженные на 12).
Мы даже можем сказать, что номер октавы представляет собой целую часть (характеристику) логарифма числа колебаний этого тона, а номер звука в данной октаве, деленный на 12 – дробную часть (мантиссу) этого логарифма.
Логарифмы в поэзии
Многообразные применения показательной (или её ещё называют, экспоненциальной) функции вдохновили английского поэта Элмера Брила на написание “Оды экспоненте”, отрывок из которой гласит:
« … Ею порождено многое из того,
Могущество ее порождений
Заранее обусловлено ее
Собственной красотой и силой,
Ибо они суть физическое воплощение
Абстрактной идеи ее.
Английские моряки любят ее и знают
Вот чудо изобретательности.
У инженера и астронома не было
Инструмента полезнее, чем она.
Даже изящнее искусства питаются ею.
Разве музыкальная гамма не есть
Набор передовых логарифмов?
И таким образом абстрактно красивое
Стало предком одного из величайших
Логарифмы в психологии
Ощущения, воспринимаемые органами чувств человека, могут вызываться раздражениями, отличающимися друг от друга во много миллионов даже миллиардов раз. Удары молота о скользкую плиту в сто раз громче, чем тихий шелест листьев, а яркость вольтовой дуги в триллионы раз превосходит яркость какой-нибудь слабой звезды, едва видимой на ночном небе. Но никакие физиологические процессы не позволяют дать такого диапазона ощущений. 
Опыты показали, что организм как бы «логарифмирует» полученные им раздражения, то есть величина ощущения приблизительно пропорциональна десятичному логарифму величины раздражения. Вредное влияние промышленных шумов на здоровье рабочих и на производительность труда побудило выработать приёмы точной числовой оценки громкости шума.
Логарифмы в живописи
Логарифмические линии в природе замечают не только математики, но и художники, например, этот вопрос чрезвычайно волновал Сальвадора Дали.
“…моей навязчивой идеей, настоящей маниакальной страстью, стала картина Я. Вермера “Кружевница”, репродукция которой висела в отцовском кабинете” Сальвадор Дали
« Уже много лет спустя я попросил в Лувре разрешение написать копию с этой картины. Потом я попросил киномеханика показать на экране репродукцию нарисованной моей копии… И обнаружил, что в «Кружевнице» я инстинктивно провел на холсте строгие логарифмические кривые…»
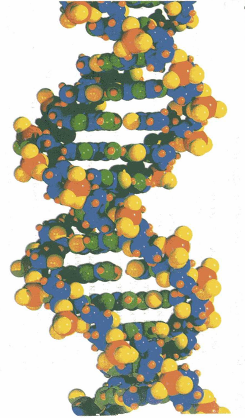
Её молекулы имеют огромную по молекулярным масштабам длину и состоят из 2-х нитей, сплетённых между собой в двойную спираль. Каждую из нитей можно сравнить с длинной нитки бус. С нитями бус мы сравниваем и белки. У белков «бусинами» являются аминокислоты 20 различных типов. У ДНК-всего 4 типа «бусин» и зовутся они нуклеотидами. «Бусины» двух нитей двойной спирали ДНК связаны между собой и строго друг другу соответствуют. Мы часто встречаем изготовление предметов по шаблону, называемому матрицей. Отливка монет или медалей, типографского шрифта. По аналогии происходящее в живой клетке восстановление двойной спирали по одной её цепи, как по матрице, так же называют матричным синтезом. 
С моей точки зрения, изобретение логарифмов по возможности можно смело поставить рядом с другими, более древним великим изобретением индусов – нашей десятичной системы счисления. Потому что, математика повсюду. Она окружает нас и она есть в каждом предмете, что мы видим или держим в руках. Я не знала, что логарифмы так тесно связаны с нашей жизнью и являются ее неотъемлемой частью. Благодаря этому проекту, я осознала, насколько важна роль логарифмов в жизни.
Результаты исследования следующие:
1.Многие природные явления не могли быть изучены без понятия логарифма;
2.Логарифмы используются для описания природных явлений астрономами, физиками, биологами;
3.Понятие логарифма широко применяется человеком во многих науках;
4.Логарифм является инструментом для вычисления радиоактивного распада, изменения количества людей в стране, зависимости скорости ракеты от ее массы, коэффициента звукоизоляции;
5.Выяснили, что, играя по клавишам современного рояля, музыкант играет, собственно говоря, на логарифмах.
Список использованной литературы:
1.Энциклопедия для детей. Т. 11. Математика. – М.: Аванта+, 1998;
3.Лиман М.М. Школьникам о математике и математиках.- М.:Просвещение,1981;
4.Алимов Ш.А. Алгебра и начала анализа.- М.:Просвещение,1994;
5.Виленкин Н.Я. Алгебра и математический анализ.- М.:Мнемозина,2004;
6. Большая электронная энциклопедия «Кирилл и Мефодий»: 2004.