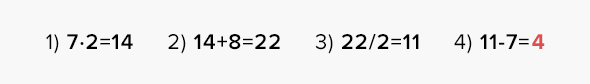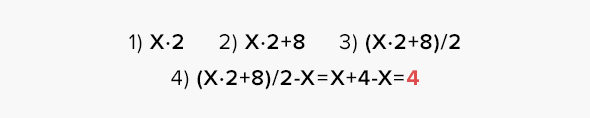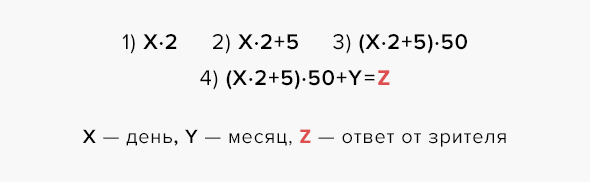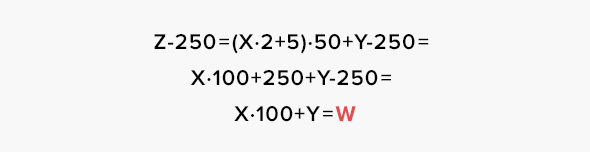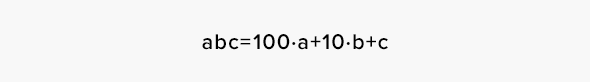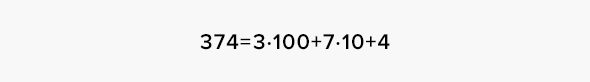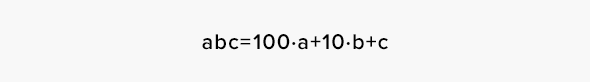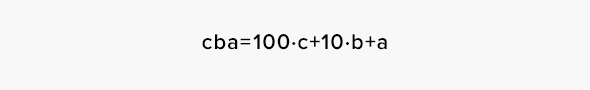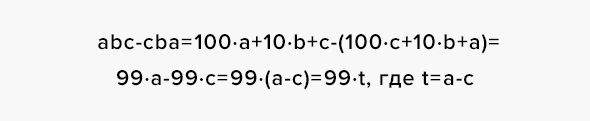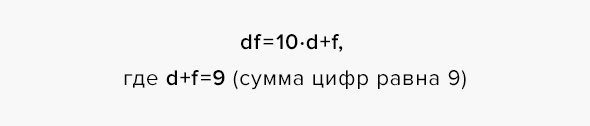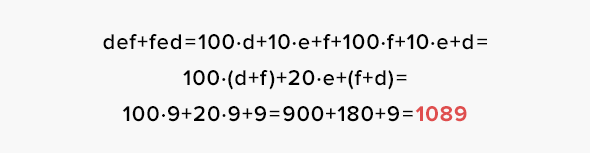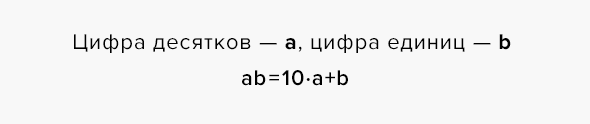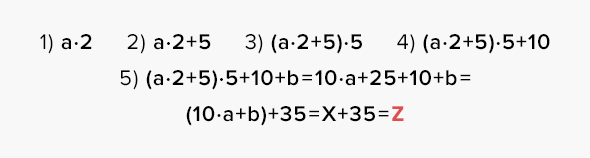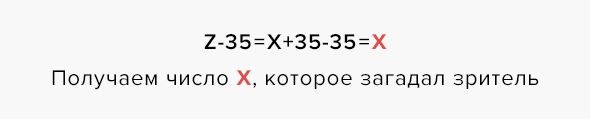Для чего нужны математические фокусы
Для чего нужны математические фокусы
Введение
«Предмет математики настолько серьезен,что полезно не упустить случая,сделать его немного занимательным»
Б. Паскаль
При первом знакомстве на уроке математики учительница пообещала угадать дату рождения каждого ученика нашего класса, если мы будем быстро и правильно выполнять предлагаемые ею арифметические действия. Сначала мы должны были день своего рождения умножить на 2, к полученному числу прибавить 5, полученный результат умножить на 50 и, наконец, прибавить к тому, что получилось номер месяца своего рождения. После того, как мы называли полученное число учительнице, она, как и обещала, угадывала дату нашего рождения и ошибалась только тогда, когда мы сами были виноваты в неправильных подсчетах. Мне очень понравился этот фокус. Ещё мне стало интересно, что лежит в основе этого фокуса. Тогда-то я и решил, что обязательно исследую вопрос о математических фокусах, узнаю их секреты, сделаю подборку фокусов и буду удивлять и развлекать своих друзей и знакомых, демонстрируя математические фокусы на уроках математики, внеклассных мероприятиях и даже на домашних праздниках.
В интернет-источниках я прочитал, что математические фокусы не пользуются особым вниманием ни у математиков, ни у фокусников. Первые считают их простой забавой, вторые – слишком скучным делом.
Но, по-моему, это совсем не так. В математических фокусах есть свой глубокий смысл.
Математические фокусы – это эксперименты, основанные на математических знаниях, на свойствах фигур и чисел, обличенные в экстравагантную форму. Понять суть того или иного эксперимента – это значит понять пусть небольшую, но очень важную математическую закономерность.
Способность человека отгадывать задуманные другими числа кажется удивительной для непосвященных. Но если мы узнаем секреты фокусов, то сможем не только их показывать, но и придумывать свои новые фокусы. А понятен секрет фокуса становится тогда, когда мы записываем предложенные действия в виде математического выражения, преобразуя которое получаем секрет отгадывания.
В своей работе я хочу доказать, что математические фокусы помогают развивать память, сообразительность, способность мыслить логически, совершенствовать навыки устного счета и, наконец, просто повышают заинтересованность учеников в математике, что должно улучшить качество их знаний.
Цель работы: исследовать математические фокусы.
Задачи:
Изучить литературу по исследуемой теме.
Продемонстрировать несколько фокусов.
Объяснить их с точки зрения математики.
Привлечь внимание одноклассников к изучению математики.
Предмет исследования: математические фокусы
Объект исследования: «секреты» математических фокусов
Методы исследования: изучение и анализ литературы по занимательной математике, самостоятельное моделирование математических фокусов.
Практическая значимость: материал может быть использован на уроках математике и на внеурочных занятиях, на математических вечерах и праздниках, при проведении математических состязаний.
Глава 1. История возникновения математических фокусов.
История возникновения математических фокусов.
Первый документ, в котором упоминается об иллюзионном искусстве, древнеегипетский папирус. В нем содержаться предания, относящиеся к 2900 году до н.э., эпохе царствования фараона Хеопса.
Изначально фокусы использовали колдуны и знахари. Жрецы Вавилона и Египта создавали огромное количество уникальных трюков с помощью прекрасных знаний математики, физики, астрономии и химии. В перечень чудес исполняемых жрецами, можно включить: раскаты грома, сверкание молний, сами собой раскрывающиеся двери храмов, появляющиеся вдруг из-под земли статуи богов, сами звучащие музыкальные инструменты, голос.
В Древней Элладе без игр не мыслилось гармоническое развитие личности. И игры древних не были только спортивными. Наши предки знали шахматы и шашки, не чужды им были ребусы и загадки. Таких игр во все времена не чуждались ученые, мыслители, педагоги. Они создавали их. С древних времен известны головоломки Пифагора и Архимеда, русского флотоводца С.О.Макарова и американца С. Лойда.
Первое упоминание о математических фокусах мы встречаем в книге русского математика Леонтия Филипповича Магницкого, опубликованной в 1703 году. Все мы знаем великого русского поэта М.Ю. Лермонтова, но не каждому известно, что он был большим любителем математики, особенно его привлекали математические фокусы, которых он знал великое множество, причем некоторые из них он придумывал сам.
На огромную познавательную и воспитательную ценность интеллектуальных игр неоднократно указывали К.Д.Ушинский, А.С.Макаренко, А.В.Луначарский. Среди тех, кто увлекался ими, были К.Э.Циолковский, К.С.Станиславский, И.Г.Эренбург и многие другие выдающиеся люди.
Отдельно хочется отметить американского математика, фокусника, журналиста, писателя и популяризатора науки Мартина Гарднера (Gardner).
Он родился 21 октября 1914 года. Окончил математический факультет Чикагского университета. Основатель (середина 50-х годов), автор и ведущий (до 1983 года) рубрики «Математические игры» журнала «Scientific American» («В мире науки»). Гарднер трактует занимательность как синоним увлекательного, интересного в познании, но чуждого праздной развлекательности. Среди произведений Гарднера есть философские эссе, очерки по истории математики, математические фокусы и «комиксы», научно-популярные этюды, научно-фантастические рассказы, задачи на сообразительность.
Особую популярность снискали статьи и книги Гарднера по занимательной математике. В нашей стране было издано семь книг Мартина Гарднера, которые увлекают читателя и подталкивают к самостоятельным исследованиям. «Гарднеровский» стиль характеризуют доходчивость, яркость и убедительность изложения, блеск и парадоксальность мысли, новизна и глубина научных идей.
Среди наших соотечественников хочется назвать имя Я.И.Перельмана. Яков Исидорович Перельман не совершил никаких научных открытий, ничего не изобрел в области техники. Он не имел никаких ученых званий и степеней. Но он был предан науке и в течение сорока трех лет нес людям радость общения с наукой. Именно с его книг начинается путешествие в увлекательный мир математики, физики, астрономии. И именно его книги помогли написать мне эту работу. Свой огромный вклад в популяризацию математики внесли Игнатьев Е.И., Кордемский Б.А. и многие другие российские ученые, педагоги, методисты.
Математические фокусы интересны именно тем, что каждый фокус основан на математических законах. Смысл их состоит в отгадывании чисел, задуманных зрителями. Миллионы людей во всех частях света увлекаются математическими фокусами. И это не удивительно. “Гимнастика ума” полезна в любом возрасте. А фокусы тренируют память, обостряют сообразительность, вырабатывают настойчивость, способность логически мыслить, анализировать и сопоставлять.
Глава 2. Математические фокусы
Фокус “Угадать задуманное число”.
Попросим любого ученика задумать число.
Потом это число ученик должен умножить на 2, прибавить к результату 8,
разделить результат на 2
и задуманное число отнять.
В результате фокусник смело называет число 4.
Разгадка фокуса:
Зритель задумал число 7
1) 7●2 = 14 2) 14 + 8 = 22 3) 22/2 = 11 4) 11 – 7 = 4
2) Х●2 2) Х●2 + 8 3) (Х●2 + 8)/2 4) (Х●2 + 8)/2 – Х = Х + 4 – Х = 4
Мы получили 4 независимо от изначально загаданного числа
Фокус “Волшебная таблица”.
Вы видите таблицу, в которой специальным образом в пяти столбцах записаны числа от 1 до 31.
Я предлагаю присутствующим задумать любое число из этой таблицы и указать, в каких столбиках таблицы находится это число.
5 простых математических фокусов
Привить любовь к математике можно разными способами, и самый необычный из них — через фокусы. Для некоторых детей этот способ может стать самым действенным — появится реальный стимул тренироваться в устном счёте и разбираться в формулах. Сайт «Фокусы. Как научиться» собрал пять самых интересных математических фокусов, а «Мел» попросил учителя математики Дмитрия Коробченко объяснить, как они работают.
Математические фокусы — самые простые в исполнении. Для них не нужен реквизит, длительная подготовка и специальное место для демонстрации. Смысл таких фокусов — в отгадывании чисел, задуманных зрителями, или в каких-нибудь операциях над ними. Все чудеса основаны на математических закономерностях, такие фокусы можно проделывать на уроках алгебры и геометрии.
И хотя вместо цифр, геометрических фигур в некоторых фокусах мы будем использовать различные предметы, все они связаны с числами. Вначале попробуйте проделать самые простые фокусы. Только помните: эти фокусы с цифрами будут получаться только тогда, когда вы научитесь быстро считать в уме (а вот, кстати, несколько советов, как этому научиться). Поэтому начинать советуем с тренировки в устном счёте, причём от меньших цифр к большим.
Обобщить секрет всех подобных математических фокусов можно следующим образом: зритель загадывает некое случайное число (или числа). Затем мы предлагаем зрителю произвести с этим числом некоторые простые арифметические операции. В итоге у зрителя получается некий финальный результат («ответ»), и наша задача — либо (1) угадать этот результат, либо (2) по этому результату, который зритель нам сообщает, предсказать исходное загаданное число.
1. Угадай число
Содержание фокуса. Попросите любого зрителя задумать число. Потом это число зритель должен умножить на 2, прибавить к результату 8, разделить результат на 2 и задуманное число отнять. В результате вы смело называете число 4.
Пример. Зритель задумал число 7.
Фокус относится к случаю (1). Загадано число X. Зритель выполняет следующие операции:
Мы получили 4 независимо от изначально загаданного числа.
2. Угаданный день рождения
Содержание фокуса. Объявите зрителям, что вы сможете угадать день рождения любого незнакомого человека, сидящего в зале. Вызовите любого желающего и предложите ему умножить на 2 число дня своего рождения. Затем пусть зритель сложит получившееся произведение и число 5 и умножит на 50 полученную сумму. К этому результату необходимо прибавить номер месяца рождения (июль — 7, январь — 1), вслух назвать полученное число. Через секунду вы называете день и месяц рождения зрителя.
Секрет. Все очень просто. В уме от того числа, которое назвал зритель, отнимите 250. У вас должно выйти трехзначное или четырехзначное число. Первая и вторая цифры — день рождения, две последние — месяц.
Фокус относится к случаю (2). Загадан день рождения. День — X, месяц — Y. Оба числа являются не более чем двузначными. Зритель выполняет следующие операции:
В уме отнимаем 250:
Так как Y — не более чем двузначное число, в получившемся числе [W=X*100+Y] месяц Y и день X никак не перемешаются. Поэтому последние две цифры числа W — это месяц Y, остальные — день X.
3. Разгаданный результат математических вычислений
Вам понадобятся: заранее приготовленные листы бумаги, карандаши или ручки, калькуляторы.
Содержание фокуса. Предложите зрителям задумать трехзначное число и записать его на бумаге. При загадывании числа должно быть выполнено одно условие: цифра сотен не должна быть равна цифре единиц и не должна быть на единицу меньше или больше неё. Если вы ещё путаетесь в сотнях и единицах, то на первом месте в трехзначных числах стоят сотни, на втором десятки, на третьем единицы (например, подойдёт число 531).
Пример. Допустим, это и есть число 531. Теперь зрители должны перевернуть задуманное число, то есть написать цифры в обратном порядке (135). Затем зрители должны взять эти два числа и из большего вычесть меньшее (531 — 135). Получившуюся разницу снова нужно перевернуть (396; 693) и сложить эти два числа (396 + 693). Потом один из зрителей должен прибавить к полученной сумме 100, второй — 200, третий — 300 и так далее. Теперь вы можете отгадать, что получилось у каждого зрителя, но при том условии, что они к своему последнему числу прибавят цифру 1 089. У первого зрителя, прибавлявшего 100, получится 1 189, у второго — 1 289, у третьего — 1 389.
Секрет фокуса. Для того чтобы узнать, что получилось, вам не нужно знать задуманное число. Главное — прибавлять к числу 1 089 то число (100, 200, 300, 400…), которое прибавлялось в самом конце. Для того чтобы не перепутать, у кого что получилось, в самом конце фокуса можно раздать карточки с цифрами 100, 200, 300 и попросить держать их при отгадывании конечного результата.
Примечание: Порой в фокусах встречаются различные операции над цифрами, которые входят в состав используемых чисел. В таком случае полезно пользоваться тем фактом, что число с цифрами a, b,c, записанное как «abc», представимо в виде:
Фокус относится к случаю (1). Загадано трёхзначное число, X, записанное как «abc». Цифра сотен — a. Цифра десятков — b. Цифра единиц — c. То есть:
Зритель выполняет следующие операции. Перевернуть число:
Вычесть из большего числа меньшее (допустим, a > c, в противном случае всё будет так же, просто a и c поменяются ролями):
Для дальнейшего действия нам необходимо представить число («abc» — «cba») как «def», то есть найти его сотни, десятки и единицы.
Все такие двузначные числа можно найти в таблице умножения (18, 27, 36, 45, 54, 63, 72, 81), и они обладают следующим свойством: сумма цифр такого числа равна 9. Запишем 9*t как «df»:
Вернёмся к числу «abc» — «cba»:
Дальнейшее действие — получившееся число снова перевернуть и сложить с предыдущим:
В результате мы получили число 1089 независимо от изначально загаданного числа. Далее к этому числу мы просим прибавить 100, 200 или 300 и получаем соответственно 1189, 1289 или 1389.
Ответ: 1189, 1289 или 1389 (в зависимости от зрителя).
4. Угадываем задуманное число
Вам понадобятся: заранее приготовленные листы бумаги (по числу зрителей), карандаши или ручки, калькуляторы.
Содержание фокуса. Предложите зрителям задумать двузначное число. Теперь пусть они умножат число его десятков на 2, прибавят к этому произведению число 5, умножат эту сумму на 5, к полученному произведению прибавят 10 и число единиц того числа, которое задумали. Пусть любой зритель скажет, что у него получилось. Вычтите из полученного результата число 35 (лучше сделать это в уме или на калькуляторе, не посвящая в свои действия зрителей), и вы сможете назвать задуманное зрителями число.
Пример. Все основано на математических закономерностях, о которых вашим зрителям знать необязательно. Как это выглядит в реальном фокусе? Например, зритель задумал число 38: 3 десятка и 8 единиц. Умножаем 3 на 2, получается 6. Прибавляем к 6 число 5, получаем 11. Умножаем эту сумму на 5, получаем 55. Прибавляем 10 и получаем 65. Прибавляем число единиц (8) задуманного числа. Получаем 73, вычитаем 35. В итоге задуманное число — 38.
Фокус относится к случаю (2). Загадано двузначное число X, записанное как «ab»:
Зритель выполняет следующие операции:
Ответ от зрителя — Z. В уме отнимаем 35:
5. Фокус с отгадыванием чисел
Вам понадобятся: заранее приготовленные листы бумаги (по числу зрителей), карандаши или ручки (по числу зрителей), калькуляторы.
Содержание фокуса. Попросите зрителей задумать какое-нибудь число. Вопрос вы можете задать абсолютно любой, например: сколько дней в неделю вы хотели бы кататься на велосипеде, есть манную кашу, не ходить в школу, бегать по лужам. Весь смысл не в вопросе, а в задуманном зрителями числе. Раздайте зрителям бумажки и ручки и попросите письменно ответить на ваш вопрос. Пусть каждый напишет, сколько дней в неделю он хотел бы есть морковку.
Теперь пусть каждый умножит это число на 2, затем к полученному числу морковок прибавит 5, после чего умножит эту сумму на 50. Теперь пусть каждый сделает следующее: если в этом году уже был день рождения, прибавить 1 750, если нет — 1 749. Теперь из этого числа каждый должен вычесть свой год рождения и к этому числу прибавить 7.
Теперь попросите любого из зрителей назвать получившуюся цифру. Должно получиться двузначное или трёхзначное число. Первая цифра — количество морковок, остальные — возраст человека.
Секрет. Секрет фокуса в тех числах, которые вы заставляете их прибавлять, отнимать, делить.
Пример. Допустим, вы загадали 2 дня в неделю для поедания морковки. Теперь умножьте 2 на 2, получится 4. Потом к 4 прибавьте 5, получится 9, затем 9 умножьте на 50, получится 450. Допустим, ваш день рождения 18 июля 1997 года. Например, сейчас сентябрь и ваш день рождения уже прошёл. Значит, прибавьте к 450 число 1 750, получится 2 200. Теперь из числа 2 200 вычтите год рождения 1997, получится 203, к этому числу прибавьте 7. Результат — 210 (2 дня и 10 лет).
Во втором случае из числа 2 199 вычтите 1 997, получится число 202, прибавьте 7, получится 209. Значит, загадано 2 дня морковки и 9 лет загадавшему.
Совет. Перед выполнением этого математического фокуса раздайте зрителям калькуляторы, чтобы они не ошиблись в вычислениях, а для себя на первое время запишите на карточке порядок действий с цифрами: на что умножить, что прибавить, из чего вычесть.
Фокус относится к случаю (2). Но этот фокус работает только в 2007 году. Для других годов нужно заменить число 1750 на другое.
Загадано число морковок X и возраст зрителя Y. Также в задаче участвуют:
4 математических фокуса, которые увлекут и взрослых, и детей
Дать ребенку 1000 примеров и 1000 задач — не лучший способ увлечь его математикой. Детям должно быть интересно, поэтому приходится иногда даже прибегать к волшебству. Например, показывать фокусы. Какие? Рассказывает руководитель проекта «Математические тропинки» Александр Маркеллов.
Чем математические фокусы могут помочь учителям и родителям
Когда я работал в «Хорошколе», я заметил, что детям сложно понять, что такое переменные и зачем они нужны. Тогда мы предложили ребятам несколько фокусов, которые иллюстрируют эту тему.
1. Фокус с переменными
Загадайте число. Прибавьте к нему 15, затем отнимите 4, потом прибавьте 5, потом отнимите из получившегося числа задуманное. У вас получилось 16.
Как мне удалось угадать ваше число?
Очень просто. И вы даже можете попробовать загадать любое другое число, но результат не изменится. Итак, чтобы понять, что произошло, нам понадобится буквенное выражение. Давайте обозначим задуманное число буквой k, ведь число может быть каким угодно. Если мы запишем все действия буквенным выражением, у нас получится:
Мы знаем, что 15 — 4 + 5 = 16, значит, мы можем упростить наше выражение. Получается:
К задуманному числу мы прибавляем 16, а потом вычитаем задуманное число. Это значит, что наше число исчезает. Теперь очевидно, что мы можем загадать любое число, но в ответе все равно получим 16.
Этот ход оказался удачным — дети остались под впечатлением. Многим из них именно это помогло разобраться в теме. С помощью переменной ребята смогли записать действия с задуманным числом в общем виде и понять механику фокуса.
Наблюдая за реакцией детей на фокусы, я заметил, что существует три уровня понимания: сначала ребенок пробует выполнить фокус, затем — проследить закономерность, и (самое сложное) пытается понять, почему так происходит.
2. Фокус с угадыванием зачеркнутой цифры
Попросите ребенка написать двузначное число, состоящее из разных цифр. Потом предложите поменять цифры местами. Получается два числа; пусть из большего он вычтет меньшее. В результате попросите зачеркнуть любую цифру и назвать оставшуюся. Теперь вы сможете назвать цифру, которую он зачеркнул.
Разбираемся, как узнать зачеркнутую цифру.
Уровень 1. Пробуем выполнить.
Например, загаданное число — 37. Меняем цифры местами — получается 73. Вычитаем из большего меньшее: 73 — 37 = 36. Ребенок зачеркивает одну цифру в этом числе и называет мне оставшуюся. Я угадываю цифру, которую он зачеркнул.
Сначала детей действительно поражает, что у них получаются разные ответы, а мне все равно удается угадать цифру.
Уровень 2. Замечаем закономерность.
Через какое-то время ребята замечают, что сумма цифр у полученного числа всегда равняется девяти. Например, если у них остается 2, то я вычитаю 2 из 9 и получаю цифру, которую они зачеркнули. Теперь ребята могут повторить этот фокус, но пока не понимают механику.
Иногда ребенок говорит: «Ха, неправильно, я зачеркнул другое число». Это значит, что он неправильно посчитал. Можно предложить ему посчитать вместе.
Уровень 3. Разбираем, как это работает.
Механику этого фокуса ребята могут понять начиная с 5-го класса. Давайте попробуем проделать фокус в общем виде.
Двузначное число записывается как «10x + y», то есть у него «x» десятков и «y» единиц. Нам нужно поменять местами цифры. Получается «10y + x».
Теперь вычтем из одного числа другое. Выглядит это так:
«10x + y — 10y — x = 9x — 9y = 9 (x — y)»
Мы видим, что это число делится на 9. Из признаков делимости на 9 мы знаем, что сумма цифр такого числа также будет делиться на 9. Отсюда мы можем сделать вывод, что сумма в ответе будет равна 9.
Кстати, интересную онлайн-вариацию этого фокуса можно найти здесь.
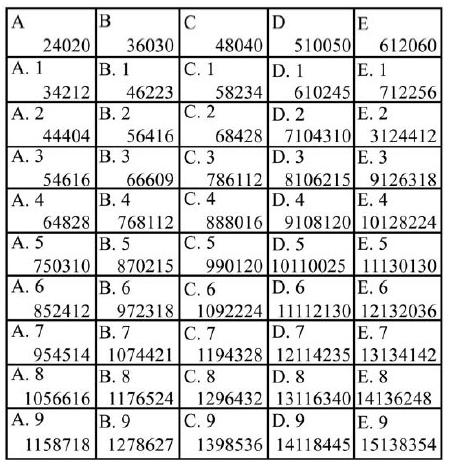
3. Фокус «Удивительная память»
Еще есть классный фокус у Перельмана. Он называется «Удивительная память». Его хорошо показывать детям, с которыми вы уже знакомы, которые знают, что память у вас совершенно обычная.
Раздайте детям такие карточки:
Ребенок называет номер любой ячейки, а вы тут же говорите, какое число там написано. Например, вам говорят: «D5», — и вы мигом отвечаете: «10110025». Числа большие, и их много, поэтому ребята точно удивятся.
Секрет фокуса в том, что значок — буква и цифра — сам указывает на число, которое написано в ячейке.
Прежде всего вы должны помнить, что буква А означает 20, В — 30, С — 40, D — 50, Е — 60.
Поэтому буква вместе с поставленной рядом цифрой означает некоторое число. Например:
А.1 = 21, С. 3 = 43, Е.5 = 65.
Из этого числа вы составляете длинное, написанное на карточке. Как это делается, покажу на примере.
Пусть вам назвали Е.4, т. е. 64.
Во-первых, складываем цифры:
Во-вторых, умножаем число на 2:
В-третьих, вычитаем из большей цифры меньшую:
В-четвертых, перемножаем цифры между собой:
Все результаты пишем рядом. Получаем:
Это и есть число, написанное на карточке в ячейке Е.4. Кратко произведенные вами выкладки можно обозначить так:
То есть умножение, удвоение, вычитание, умножение.
После разбора фокуса можно поговорить с ребятами про кодирование. Наверняка они не знают, что человек, сам не замечая, передает закодированное сообщение.
4. Фокус с монетами
Этот фокус я тоже нашел у Перельмана. Он отлично подходит для изучения четности.
Возьмите в одну руку двухрублевую монету, в другую — пятирублевую. Не показывайте и не говорите мне, где какая монета. Я угадаю это сам. Для этого вам нужно сделать следующее: утройте ту монету, что в правой, и удвойте ту, что в левой. Сложите полученные числа и скажите мне, какая сумма: четная или нечетная. Этого мне достаточно, чтобы безошибочно определить, какая монета зажата у вас в правой руке, а какая — в левой.
Давайте запишем, что происходит, рассматривая четность числа. У нас есть два варианта: в правой руке у вас может быть либо четная монета, либо нечетная.
Разберем первый случай, когда в правой руке у вас находится два рубля. Тогда
При умножении четного числа на нечетное мы получаем четное число, значит
В этом случае у нас получается четное число.
Теперь посмотрим на другой случай, когда в правой руке у нас монета номиналом 5 рублей.
(н х н) + (ч х ч) = н + ч = н
В этом случае мы всегда будем получать нечетное число.
Используйте эти нехитрые фокусы в обучении. Ребята поймут, что математика — интересная и полезная наука, и будут ждать ваших занятий с нетерпением.