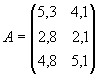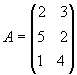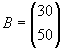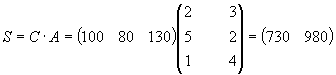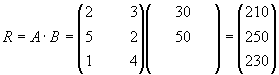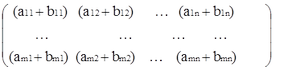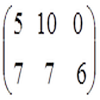Для чего нужны матрицы в экономике
Для чего нужны матрицы в экономике
Математика.Дифференциальные и интегральные уравнения
Донецкий национальный университет экономики и торговли имени
Михаила Туган-Барановского, Украина
Применение матриц в экономике
В данной статье мы рассмотрим использования матриц в экономике. Для этого нам необходимо будет проанализировать решения экономической задачи и сделать определенные выводы.
Матрица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате, решение систем линейных уравнений сводится к операциям над матрицами.
С помощью матриц удобно записывать некоторые экономические зависимости. Например, таблица распределения ресурсов по отдельным отраслям экономики (усл. ед.):
Может быть записана в компактной форме в виде матрицы распределения ресурсов по отраслям:
Общую стоимость сырья можно вычислить и в другом порядке: вначале вычислим матрицу стоимостей затрат сырья на единицу продукции, т.е. матрицу:
а затем общую стоимость сырья:
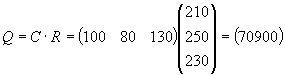
Проанализировав использования матриц в экономике, мы пришли к выводу, что достоинства матриц состоят в том, что они используют широкий набор стратегически значимых переменных; указывают направление движения ресурсов. Среди недостатков этого инструмента: не обеспечивает реальных рекомендаций по разработке специфических стратегий; по ней невозможно определить сферы бизнеса, которые готовы стать победителями. Также матрицы позволяют с минимальными затратами труда и времени обрабатывать огромный и весьма разнообразный статистический материал, различные исходные данные, характеризующие уровень, структуру, особенности социально-экономического комплекса.
ПРИМЕНЕНИЕ МАТРИЦ В ЭКОНОМИКЕ
Использование ресурсов в различных сферах экономики :
Эту таблицу можно записать и охарактеризовать в виде матрицы :
Наглядным примером также может нам послужить следующая задача :
Некая фирма производит различную продукцию С1, С2, С3 и на изготовку этого продукта используется материал К1, К2:
где элемент аij показывает сколько сырья j-того типа может быть потрачено внутри организации на производство продукции i-того типа. Цена каждого вид сырья равна:
а планирование выпуска продукции равно В = (110 150 70).
Из этого следует как, мы получим: расходы на материал
К1 = 2 × 110 + 5 × 150 + 8 × 70 = 1530,
а цена другого материала
К2 = 5 × 110 + 3 × 150 + 7 × 70 = 1490.
Р = 1530 × 70 + 1490 × 50 = 181600 может быть представлена в виде вектора:
Р = К × С = (ВА)С = 181600.
Суммарная цена материала равна:
P = B * Z = (110 150 70) =181600
Идентичность всех выше перечисленных результатов (181600) была получена благодаря правильному выполнению семантического закона умножения векторов : (ВА)С = В(АС).Этот закон ярко иллюстрирует пример такого, что решая через любой вид решения матриц можно добиться одинаковости всех результатов. [2]
В таблице 2 проиллюстрированы сведения о работе 5 различных фирм, которые выпускают 4 вида товара с потреблением 3-х видов сырья, так же количество времени работы абсолютно каждой фирмы в году и стоимости всех видов материала.
Стоимость материалов продукции
Количество полных рабочих дней в году
Стоимость разных видов материала
1) Эффективность и плодотворность всех фирм по каждому виду продукции;
2) Нужда всех фирм по каждому виду материала;
3) Совокупность кредитования фирм для закупки и переработки материалов, которые необходимо для выпуска продукции указанных видов и количеств фирм.
Выстроим матрицу производства фирм по всем типам продукции:
М атрица затрат материалов на единицу продукции представлена как:
Все издержки по видам материала на фирмах можно полностью расписать как D * C:
где j-я строка соответствует номеру типа материала, а i-й столбец – номеру фирмы согласно таблице (j =1, 2, 3; i =1, 2, 3).
Введем вектор цены материала: Q = (70, 80, 90)
P = QDC 1= (8238300 8979200 4937400)
4. Конкина В.С., Минат В.Н. Методика экономических исследований в АПК России / В.С. Конкина., В.Н. Минат. // Актуальные проблемы науки и практики XXI века: материалы Всероссийской научно-практ. конференция; Ряз фил-л НОУ ВО «Московская академия экономики и права». Казань: Бук, 2016. С.20-25.
Творческие проекты и работы учащихся
В процессе работы над индивидуальным проектом по математике «Матричная алгебра в экономике» учеником 11 класса гимназии были рассмотрены матричные методы в экономике на примерах решения задач экономического содержания. В работе доступно объясняется, что такое «математическая матрица» и как ее применять.
Подробнее о проекте:
Готовый творческий и исследовательский проект по математике «Матричная алгебра в экономике» наглядно демонстрирует взаимосвязь математики и экономики, определяет роль математических методов в анализе экономических процессов, объектов и явлений.
Оглавление
Введение
1. Немного истории.
2. Матрицы и операции над ними.
3. Решение с помощью матриц экономических задач.
Заключение
Используемая литература
Приложение
Введение
На современном этапе экономические взаимоотношения между субъектами образуют экономические системы со сложной структурой, большим количеством элементов и связей между ними, которые являются причиной почти всех особенностей экономических задач.
На внедрение и развитие математических методов в решении экономических задач, большое влияние оказало создание и развитие современной вычислительной техники. Вычислительная техника нового поколения позволила применять на практике множество новых методов, которые были описаны ранее только в теории или объяснялись на простых примерах.
Но никакая вычислительная техника не способна заменить человека и поэтому, люди должны уметь эффективно использовать теоретические знания в области математики в экономике, а именно, уметь правильно решать экономические задачи при помощи матричных методов.
Также матрицы позволяют с минимальными затратами труда и времени обрабатывать огромный и весьма разнообразный статистический материал, различные исходные данные, характеризующие уровень, структуру, особенности социально-экономического комплекса.
В современных условиях особенно актуально использование матриц для формирования баз данных, ведь вся информация обрабатывается и хранится в форме матриц.
Матрицы можно эффективно использовать не только в науке, но и применять их на практике в крупных предприятиях для решения современных экономических задач. Матричный метод позволяет упростить работу человека, уменьшить количество критериев и альтернатив для выбора и получать выгодные варианты решения для выхода из различных экономических ситуаций.
В данной работе содержится информация о самих матрицах, операциях над ними и на примерах показано, как можно решать экономические задачи при помощи матриц.
Актуальность. Математика и экономика – две на первый взгляд далекие друг от друга науки. Однако, взаимосвязь между этими науками, роль математических методов в анализе экономических процессов, объектов и явлений были отмечены учеными ещё в XVII веке.
В XX веке происходило бурное проникновение математических методов в самые разные науки, в том числе и в экономику. В настоящее время этот процесс ещё более активизировался, благодаря развитию вычислительной техники. Поэтому современному экономисту необходима основательная математическая подготовка. И в число наиболее важных математических дисциплин для экономиста входит линейная алгебра, а именно матричная алгебра. В этом я вижу актуальность выбранной темы.
Цель. Рассмотреть матричные методы в экономике на примерах решения задач экономического содержания.
Гипотеза Используются ли в экономике те математические знания, которыми мы владеем
Предмет исследования: Матричные методы.
Объект исследования: Математические понятия и законы, экономические модели.
Методы исследования: Теоретическое изучение материала, образцы решения экономических задач.
Немного истории
В это же время был предложен другой метод решения систем линейных уравнений, который тоже носит имя своего изобретателя, это «метод Гаусса». Заметим, что «правило Крамера» работает только для систем с ненулевым детерминантом (определителем системы), тогда как «метод Гаусса» работает для любой системы линейных уравнений.
Огромный вклад в развитие теории матриц в середине XIX внесли такие известные ученые как Уильям Гамильтон и Артур Кэли. Наряду с ними развивали данную теорию немецкие математики Карл Вейерштрасс и Фердинанд Георг Фробениус, а также, французский математик Мари Энмон Камиль Жордан. В 1850 году Джеймс Сильвестр ввел современное понятие матрицы. Под влиянием работ этих великих ученых в математике появился новый раздел, который был назван матричной алгеброй.
Матрицы и операции над ними
Матрица – это прямоугольная таблица, представляющая собой совокупность строк и столбцов. Размерностью матрицы называется величина m×n, где m-число строк, n-число столбцов.
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате, решение систем линейных уравнений сводится к операциям над матрицами. А множество экономических задач можно свести к системам линейных уравнений.
Операции с матрицами не слишком громоздки и не требуют чрезмерно кропотливой работы; напротив, матричную алгебру во многих случаях ценят именно за краткость, простоту и ясность. С помощью матричной алгебры можно выразить в математической форме многие задачи, как большие, так и малые, независимо от их размерности.
Основные операции с матрицами рассмотрены в Приложении.
Решение с помощью матриц экономических задач
Для наглядности перейдём к рассмотрению задач.
1. С помощью матриц удобно записывать некоторые экономические зависимости. Одним из примеров может послужить таблица распределения ресурсов по различным отраслям экономики.
Таблица: Распределение ресурсов
| Ресурсы | Промышленность | Сельское хозяйство | Торговля |
| Трудовые ресурсы | 4,8 | 6,7 | 7,1 |
| Водные ресурсы | 3,1 | 2,5 | 5,8 |
| Электроэнергия | 5,6 | 4,3 | 3,4 |
Так, например, элемент матрицы а22 = 2,5 показывает, сколько водных ресурсов потребляет сельское хозяйство, а элемент матрицы а13 = 7,1 показывает, сколько трудовых ресурсов потребляет торговля.
2. Рассмотрим такую ситуацию. Некоторая фирма занимается реализацией четырех видов товаров в трех районах. Данные об уровне продаж товаров по районам образуют матрицу.
Величина aij, которая находится в i-й строке и j-м столбце матрицы A, обозначает количество j-го товара, проданное в i-м районе. Таким образом, строки матрицы соответствуют районам, а столбцы – видам товаров. Обозначим через ci, i= 1, 2, 3, 4 цены на реализуемые товары. Они образуют матрицу-столбец.
Если хотим найти суммарный объем продаж в первом районе, то мы должны вычислить следующее выражение:
a11c1 + a12c2 + a13c3 + a14c4,
которое является скалярным произведением первой строки матрицы A на столбец цен C. И строчка, и столбец являются арифметическими 4-х мерными векторами. Про выражение (a11c1 + a12c2 + a13c3 + a14c4) говорят, что оно получено при умножении первой строки матрицы A на столбец C.
Производя такое умножение на столбец C второй и третьей строк, получаем еще две величины, которые представляют собой суммарные продажи во втором и третьем районах. Эти две величины вместе с ранее найденной величиной образуют вектор суммарных продаж.
В этом примере фактически применено действие умножения матриц.
Решение. Нужно составить матрицы, характеризующие весь интересующий нас экономический спектр производства, а затем при помощи соответствующих операций над ними получить решение данной задачи.
Каждый столбец этой матрицы соответствует дневной производительности отдельного предприятия по каждому виду продукции. Следовательно, годовая производительность j-го предприятия по каждому виду продукции получается умножением j-гo столбца матрицы А на количество рабочих дней в году для этого предприятия (j = 1, 2, 3, 4, 5). Таким образом, годовая производительность каждого предприятия по каждому из изделий описывается матрицей.
Матрица затрат сырья на единицу изделия (эти показатели по условию одинаковы для всех предприятий) имеет вид
Дневной расход по типам сырья на предприятиях описывается произведением матрицы В на матрицу А:
где i-я строка соответствует номеру типа сырья, а j-й столбец — номеру предприятия согласно табл. 16.2 (i = 1, 2, 3; j = 1, 2, 3, 4, 5). Ответ на второй вопрос задачи получим по аналогии с матрицей Агод умножением столбцов матрицы ВА на соответствующие количества рабочих дней в году для предприятий — это годовая потребность каждого предприятия в каждом виде сырья:
Введем вектор стоимости сырья.
Тогда стоимость общего годового запаса сырья для каждого предприятия получается умножением вектора 
Следовательно, суммы кредитования предприятий для закупки сырья определяются соответствующими компонентами вектора 
4. Множество экономических задач можно свести к системам линейных уравнений. Для наглядного примера рассмотрим следующую задачу.
Предположим, что кривая спроса на автомобили для некоторого периода времени может быть описана уравнением
где x1 – цена автомобиля (в долларах), а x2 – их количество.
Предполагаем также, что уравнение кривой предложения имеет вид:
Объединим уравнения в систему.
Эту систему, конечно, легко решить непосредственно, например методом подстановки. Но мы перейдем от системы к матричному уравнению.
Напрашивается решение этого уравнения в виде:
Но операции деления матриц нет. Но есть операция вычисления обратной матрицы. Подумаем, как мы решаем уравнение 5X = 7? Мы пишем, не особенно задумываясь, X = 7/5. а как записать ответ, не пользуясь делением? Это возможно: X = 5-1•7 или 7•5-1.
Обратная матрица A-1 должна обладать свойством A-1A = E, где E – единичная матрица.
Умножим слева на A-1 обе части матричного уравнения AX = В и получим равенство
Но так как A-1A =E, а EX = X, то мы приходим к равенству
Это означает, что равновесная цена на автомобили X = 4200 долларов, а объем продаж X = 39000 штук.
Подобные задачи удобно решать методом Гаусса – методом последовательного исключения переменных, который заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Преобразования Гаусса можно проводить не только с уравнениями системы, но и с матрицей их коэффициентов.
Заключение
Проанализировав применение матричной алгебры в экономике, можно прийти к выводу, что использование матриц имеет свои достоинства и недостатки.
Недостатки заключаются в том, что матричная алгебра не обеспечивает реальных рекомендаций по разработке специфических стратегий; по матрицам невозможно определить сферы бизнеса, которые готовы стать победителями.
Достоинства же применения матриц в том, что они используют широкий набор стратегически значимых переменных; указывают направление движения ресурсов; позволяют с минимальными затратами труда и времени обрабатывать огромный и весьма разнообразный статистический материал, различные исходные данные, характеризующие уровень, структуру, особенности социально-экономического комплекса.
При наличии отрицательных моментов применения матричной алгебры положительная часть значительно обширнее.
Из выше рассмотренного можно сделать вывод, что роль матриц в экономике очень и очень велика. Ведь благодаря их использованию можно гораздо быстрее, чем с использованием какого-либо другого математического аппарата, и проще решить многие экономические задачи, что чрезвычайно важно для экономистов.
Используемая литература
Приложение. Операции над матрицами
Линейные операции над матрицами.
Определение 1. Матрицей называется прямоугольная таблица:
A = 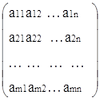
Число m ее строк и число n ее столбцов называют размерами матрицы А. Про матрицу А говорят, что она размером m×n. Обозначим Mm×n множество матриц размером m×n (m строк и n столбцов).
Определение 2. Пусть A=(aij) и B=(bij) – две матрицы размером m×n.
Действие сложения определено для матриц одинакового размера
C=A +B=
Произведением матрицы A на число α называется матрица αA с элементами (αaij).
αA=
Операции сложения матриц и умножения матрицы на число называют линейными операциями.
Презентация на тему «Применение матриц в экономике»
Описание презентации по отдельным слайдам:
Матрицы. Применение матриц в экономике. Преподаватель ДППК Трохимюк О.В.
Математика является универсальным языком, который широко применяется во всех сферах человеческой деятельности. Во многих экономических и профессиональных дисциплинах необходимы знания о матрицах, операциях над ними, умения решать прикладные задачи с помощью матриц. Актуальность этой темы усиливается в связи с широким использованием матриц в экономических дисциплинах: финансы, экономика предприятий, статистика, логистика, экономико – математическое моделирование и др.
«Скажи мне — и я забуду. Покажи мне — и я запомню. Позволь мне сделать — и это станет моим навсегда».
Основным применением матриц было решение линейных уравнений. После развития теории определителей в конце 17-го века, Габриэль Крамер начал разрабатывать свою теорию в 18-ом столетии и опубликовал «правило Крамера» в 1751 году. Примерно в этом же промежутке времени появился «метод Гаусса». Теория матриц начала своё существование в середине XIX века в работах Уильяма Гамильтона и Артура Кэли (Кэли, Кейли (Cayley) Артур английский математик). Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г.
Применение матриц Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами. К середине XIX в. матрицы стали самостоятельными объектами математических исследований. К этому времени были сформулированы правила сложения и умножения матриц. Основную роль в их разработке сыграли работы Гамильтона, Кэли и Сильвестра (J.J.Sylvester, 1814–1897). Современное обозначение матрицы предложил Кэли в 1841 году. Исследования Вейерштрасса (K.Th.W.Weierstrass, 1815–1897) и Фробениуса (F.G.L. Frobenius, 1849–1917) далеко продвинули теорию матриц, обогатив ее новым содержанием.
Кэли, Кейли (Cayley) Артур английский математик Джеймс Сильвестр – один из основоположников теории матриц. Фердинанд Георг Фробениус – немецкий математик.
Карл Теодор Вильгельм Вейерштрасс
План Применение матриц в экономике.
Ключевые понятия и термины: матрица; определитель матрицы; квадратная матрица; прямоугольная матрица; виды матриц; обратная матрица; алгоритм нахождения обратной матрицы; алгебраические дополнения.
Литература 1. Алгебра и начала математического анализа: учебник для общеобразоват. организаций: базов. и углубл. уровни / Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева и др. – М.: Просвещение, 2016. – 463 с. 2. Высшая математика для экономистов: Учебное пособие. – К.: Знания, Макаренко В.А., 2008 – 517 с. 3. Математика: Учебник / О.М. Афанасьева, Я.С. Бродский и др. – К.: Высшая школа, 2001. 4.Дидактический материал по математике: Учебное пособие / О.М. Афанасьева, Я.С. Бродский и др. – К.: Высшая школа, 2001. 5. Практические занятия по математике. Н.В. Богомолов. – М.: Высшая школа, 1983.
Вопросы к теме Что такое матрицы и зачем они нужны? Какие виды матриц существуют? Как найти определитель матрицы? Какие операции можно выполнять над матрицами? Какая матрица называется обратной? Как найти обратную матрицу? Как решить систему трех линейных уравнений с тремя переменными методом обратной матрицы?
Актуализация опорных знаний студентов Вопросы для фронтального опроса студентов 1. Как вычисляется определитель второго порядка? 2. Вычислить определитель второго порядка:
Актуализация опорных знаний студентов Вопросы для фронтального опроса студентов 1. Как вычисляется определитель второго порядка? 2. Вычислить определитель второго порядка: 3.Вычислить определитель третьего порядка разложением определителя по элементам 1 строки:
Актуализация опорных знаний студентов Вопросы для фронтального опроса студентов 1. Как вычисляется определитель второго порядка? 2. Вычислить определитель второго порядка: 3.Вычислить определитель третьего порядка разложением определителя по элементам 1 строки:
4. Проведем короткий анализ домашней работы. 5. Проверить определитель второго порядка из домашнего задания 6. Проверить определитель третьего порядка из домашнего задания
1. Матрица – это упорядоченная таблица чисел которая имеет m строк и n столбцов.
Транспонирование матрицы Если в данной матрице поменять строки и столбцы местами, то получится транспонированная матрица данной.
Где ещё применяются матрицы? Теперь подробнее остановимся на некоторых областях применения матриц. Понятие матрицы и основанный на нем раздел математики – матричная алгебра – имеют чрезвычайно важное значение для экономистов. Так как значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное – компактной матричной форме. С помощью матриц удобно записывать некоторые экономические зависимости.
Ресурсы Отрасли экономики Промышленность Сельское хозяйство Электроэнергия 5,3 4,1 Трудовые ресурсы 2,8 2,1 Водные ресурсы 4,8 5,1
2. Действия над матрицами. Матрицы можно умножать на число, складывать, умножать на матрицу. Умножить матрицу на число – это значит, каждый элемент умножить на это число. Складывать можно матрицы одного размера. Суммой двух матриц является матрица, элементы которой равны сумме соответствующих элементов данных матриц. Так же определяется и разность.
Свойства сложения и умножения матриц.
Матрицы можно подвергать элементарным преобразованиям: 1. Можно менять местами строки и столбцы. 2. Можно строку (столбец) умножать на одно и то же число. 3. К некоторой строке или столбцу можно прибавить другую строку (столбец), умноженную на некоторое число. Такие преобразования приводят к замене строк или столбцов строками (столбцами), состоящими из нулей, которые надо удалять из матрицы для рассмотрения матрицы меньшего размера.
Проверка правильности вычислений: (Сделать вывод. Для матриц А и справедлив переместительный закон умножения). Делаем вывод. Для матриц А и справедлив переместительный закон умножения. Ответ:
Пример Определить обратную матрицу для матрицы
Пример Определить обратную матрицу для матрицы
Пример Определить обратную матрицу для матрицы
Пример Определить обратную матрицу для матрицы
Пример Определить обратную матрицу для матрицы
Пример Определить обратную матрицу для матрицы
Пример Определить обратную матрицу для матрицы
Пример Определить обратную матрицу для матрицы Решение. Вычислим определитель матрицы А: то для матрицы А существует обратная матрица Запишем алгебраические дополнения элементов матрицы А: Обратная матрица имеет вид:
Теперь будем находить алгебраические дополнения:
Теперь будем находить алгебраические дополнения:
Теперь будем находить алгебраические дополнения:
Задача 1. В цехе предприятия изготовляют две модели женской одежды. На изготовление первой модели тратят 2 м ткани, на изготовление второй – 3 м. При этом расходы рабочего времени на производство этих моделей составляют соответственно 4 и 5 часов. Известно, что недельный запас ткани – 100 м, а рабочее время ограниченно 190 часов. Составить такой план недельного изготовления этих моделей одежды, при которой полностью используют ресурсы (ткань и рабочее время).
Применение матриц в экономике Задача 1. В цехе предприятия изготовляют две модели женской одежды. На изготовление первой модели тратят 2 м ткани, на изготовление второй – 3 м. При этом расходы рабочего времени на производство этих моделей составляют соответственно 4 и 5 часов. Известно, что недельный запас ткани – 100 м, а рабочее время ограниченно 190 часов. Составить такой план недельного изготовления этих моделей одежды, при которой полностью используют ресурсы (ткань и рабочее время). Обозначим через и количество единиц недельного выпуска первой и второй моделей соответственно. По условию задачи составим систему линейных уравнений
Применение матриц в экономике Задача 1. В цехе предприятия изготовляют две модели женской одежды. На изготовление первой модели тратят 2 м ткани, на изготовление второй – 3 м. При этом расходы рабочего времени на производство этих моделей составляют соответственно 4 и 5 часов. Известно, что недельный запас ткани – 100 м, а рабочее время ограниченно 190 часов. Составить такой план недельного изготовления этих моделей одежды, при которой полностью используют ресурсы (ткань и рабочее время). Обозначим через и количество единиц недельного выпуска первой и второй моделей соответственно. По условию задачи составим систему линейных уравнений
Следовательно, для полного использования ресурсов еженедельно нужно изготовлять 35 единиц первой и 10 единиц второй моделей одежды. Вывод. Заметим, что при решении экономических задач удобно использовать матричный способ. Почему? Вычислив один раз обратную матрицу и изменяя ограничение на ресурсы (ежедневные, еженедельные, ежемесячные, ежегодные и тому подобное), будем получать каждый раз из равенства соответствующий план выпуска продукции. Заметим, что применение матриц в этой задаче привело к наглядности, упрощению и компактности вычислений.
Задача № 2. Рассмотрим упрощенную модель финансовой математики, которую условно называют «портфельными инвестициями». В реальной жизни одним из источников финансирования являются международные инвестиции. Страна может получать и давать международные займы, принимать и инвестировать за границу капитал. Продажа активов в любой фирме (права собственности, ценные бумаги, золото и т.п.) означает прилив капитала в страну. Среди инвестиций есть портфельные – вложение капитала в иностранные ценные бумаги, которые не дают инвестору права реального контроля над объектом инвестирования. Такие инвестиции основываются, как правило, на частном капитале.
Подведение итогов занятия. Какие основные определения и понятия вы усвоили на занятии? С каким способом решения системы вы сегодня познакомились?
Подведение итогов занятия. Какие основные определения и понятия вы усвоили на занятии? познакомились с матрицами, с видами матриц, с действиями над матрицами, с обратной матрицей, с алгоритмом нахождения обратной матрицы. С каким способом решения системы вы сегодня познакомились? Метод обратной матрицы.
Подведение итогов занятия. Благодарю за работу на занятии. Подсчитываем поощрительные баллы. Оценки комментируются и выставляются в журнал.
Проверьте сами. Сделайте вывод! Квадрат Пифагора! Дата Рождения! (25.07.1998)
Квадрат Пифагора. Так называемая ‘психоматрица’, придуманная древнегреческим ученым Пифагором, относится к самым популярным расчетам в нумерологии Квадрат Пифагора 111 характер,сила воли; 4здоровье, красота; 77 удача,везение; 2 энергетика,харизма; 55 логика,интуиция; 8 чувство долга; 3 познание,творчество; — трудолюбие,мастерство; 99 память,
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Номер материала: ДБ-098705
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Во всех педвузах страны появятся технопарки
Время чтения: 1 минута
Рособрнадзор не намерен упрощать ЕГЭ в 2022 году из-за пандемии
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
В России стартует пилотный проект по реабилитации детей-инвалидов
Время чтения: 2 минуты
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Число участников РДШ за 2021 год выросло в три раза
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.