Для чего нужны наглядные изображения предметов

Общие сведения. 1. Для чего нужны наглядные изображения предметов?

ОСНОВЫ МАШИНОСТРОИТЕЛЬНОГО ЧЕРЧЕНИЯ

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Для чего нужны наглядные изображения предметов?

2. Назовите способы построения наглядных изображений?

3. Что такое аксонометрия?

4. Как получают аксонометрический чертеж?

5. Какую проекцию называют вторичной?

6. Что такое коэффициент искажения в аксонометрии?

7. Какие виды аксонометрии вы знаете?

8. Чем характеризуется прямоугольная изометрия?

9. Каков масштаб изображения в стандартной прямоугольной изометрии?

10. Как построить изометрию окружности?

11. Чем характеризуется прямоугольная диметрия?

12. Каков масштаб изображения в стандартной прямоугольной диметрии?

13. Как построить диметрию окружности?

14. Какие правила вы знаете по определению направления большой оси эллипса в изометрии и диметрии?

15. Чему равна большая и малая оси в изометрии и диметрии?

Глава 13. ИЗОБРАЖЕНИЕ ПРЕДМЕТОВ

Главным элементом в решении графических задач в инженерной графике является чертеж. Под чертежом подразумевают графическое изображение предметов или их частей. Чертежи выполняются в строгом соответствии с правилами проецирования с соблюдением установленных требований и условностей. Причем правила изображения предметов или их составных элементов на чертежах остаются одинаковыми во всех отраслях промышленности и строительства.

Изображение предмета на чертеже должно быть таким, чтобы по нему можно было установить форму его в целом, форму отдельных его поверхностей, сочетание и взаимное расположение отдельных его поверхностей. Иными словами, изображение предмета должно давать полное представление о его форме, устройстве, размерах, а также о материале, из которого изготовлен предмет, а в ряде случаев включать сведения о способах изготовления предмета. Характеристикой величины предмета на чертеже и его частей являются их размеры, которые наносятся на чертеже. Изображение предметов на чертежах выполняют, как правило», в заданном масштабе.

Изображения предметов на чертеже должны быть размещены так, чтобы поле его было равномерно заполнено. Число изображений на чертеже должно быть достаточным для получения полного и однозначного представления о нем. В то же время на чертеже должно быть только необходимое количество изображений, оно должно быть минимальным, т. е. чертеж должен быть лаконичным и содержать минимальный

объем графических изображений и текста, достаточных для свободного чтения чертежа, а также его изготовления и контроля.

Видимые контуры предметов и их граней на чертежах выполняются сплошной толстой основной линией. Необходимые невидимые части предмета выполняют при помощи штриховых линий. В случае, если изображаемый предмет имеет постоянные или закономерно изменяющиеся поперечные сечения, выполняется в требуемом масштабе и не помещается на поле чертежа заданного формата, его можно показать с разрывами.

Правила построения изображений на чертежах и оформления чертежей приведены и регламентируются комплексом стандартов «Единой системы конструкторской документации» (ЕСКД).

Изображение на чертежах может быть выполнено различными способами. Например, с помощью прямоугольного (ортогонального) проецирования, аксонометрических проекций, линейной перспективы. При выполнении машиностроительных чертежей в инженерной графике чертежи выполняют по методу прямоугольного проецирования. Правила изображения предметов, в данном случае изделий, сооружений или соответствующих составных элементов на чертежах установлены ГОСТ 2.305—68.

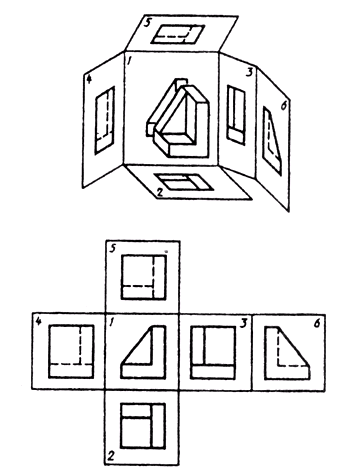
При построении изображений предметов методом прямоугольного проецирования предмет располагают между наблюдателем и соответствующей плоскостью проекции. За основные плоскости проекций принимают шесть граней куба, внутри которого располагается изображаемый предмет (рис. 165, а). Грани 1,2 и 3 соответствуют фронтальной, горизонтальной и профильной плоскостям проекций. Грани куба с полученными на них изображениями совмещают с плоскостью чертежа (рис. 165, б). При этом грань 6 можно расположить и рядом с гранью 4.

Изображение на фронтальной плоскости проекций (на грани 1) считается главным. Предмет располагают относительно фронтальной плоскости проекций так, чтобы изображение давало наиболее полное представление о форме и размерах предмета, несло наибольшую информацию о нем. Это изображение называют главным.

В зависимости от своего содержания изображения предметов разделяют на виды, разрезы, сечения.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Для чего нужны наглядные изображения предметов

При построении комплексного чертежа изображаемый предмет обычно располагают так, чтобы направления трех главных измерений (длина — высота — ширина — были бы параллельны координатным осям плоскостей проекций (рис. 2.31, а). Обычно . В этом случае на каждой из проекций два измерения проецируются в натуральную величину без искажения, но третье измерение проецируется в точку, т. е. отсутствует. Поэтому для полного представления о форме предмета необходимы еще одна или несколько проекций на другие плоскости проекций. Несколькими проекциями можно добиться полной информативности комплексного чертежа о форме предмета. Однако на таком чертеже теряется одно из основных качеств изображения, а именно наглядность. Представить истинную пространственную форму предмета по такому чертежу бывает достаточно трудно, особенно для предметов сложной геометрической формы.

Для того чтобы чертеж стал наглядным, необходимо построить проекцию предмета, на которой ни одно из главных измерений не проецировалось бы в точку. Для этого предмет следует соответствующим образом расположить перед плоскостями проекций, чтобы он был виден сразу с трех сторон: спереди, сверху и слева (рис. 2.31, б).

Наглядные изображения могут быть выполнены в свободной манере с приближенным соблюдением соотношений размеров по осям, а могут быть построены по определенным законам. В наглядных изображениях искажаются углы между координатными осями (рис. 2.31, е) и линейные размеры по этим осям. Отношение длины проекции отрезка, параллельного координатной оси, к его истинной длине определяет коэффициент искажения размера по этой оси: — коэффициент искажения вдоль оси х; — то же вдоль оси то же вдоль оси Наглядные изображения, построенные с заданными коэффициентами искажения по главным измерениям и углами между координатными осями, называют аксонометрическими роекциями.

Для прямоугольных аксонометрических проекций существует зависимость между коэффициентами искажения

Правила построения стандартных аксонометрических проекций устанавливает ГОСТ 2.317-69. Наибольшее применение на практике имеют следующие аксонометрические проекции: изометрическая и днметрическая прямоугольные проекции, косоугольная фронтальная диметрическая проекция (рис. 2.32).

Рис. 2.31. Построение наглядного изображения. а — комплексный чертеж; наглядное изображение; в — расположение координатных осей

Изометрическая прямоугольная проекция предполагает, что коэффициенты искажения по всем трем осям одинаковы:

и в соответствии с вышепрннятой формулой равны 0,82. Углы между координатными осями также одинаковы, и равны (рис. 2.33,а). Как правило, при построении изображения предмета в изометрической проекции в целях упрощения используют приведенный коэффициент искажения -Изображение в этом случае получается несколько увеличенным, как бы построенным в масштабе

Диметрическая прямоугольная проекция предполагает одинаковыми коэффициенты искажения по двум осям. В стандартной форме диметрической прямоугольной проекции приняты одинаковыми коэффициенты искажения по осям и 2, а по оси у — в 2 раза меньший, т.е. Действительные коэффициенты искажения равны В целях упрощения построения диметрическую проекцию выполняют без искажения по осям и с коэффициентом искажения по оси Положение координатных осей для днметрической прямоугольной проекции приведено на рис.

Косоугольная фронтальная диметрическая проекция имеет те же коэффициенты искажения, что и прямоугольная диметрическая проекция, но выгодно отличается от нее более удобным расположением координатных осей, что упрощает геометрические построения.

Из других косоугольных аксонометрических проекций, которые рекомендует следует назвать изометрические фронтальную и горизонтальную проекции, каждая из которых выполняется без искажения по всем трем осям: (Подробнее об этих проекциях см.

Необходимо остановиться на построении проекций окружностей в аксонометрии. Как правило, проекциями окружностей являются эллипсы (рис. 2.34). Исключение составляет косоугольная фронтальная диметрическая проекция окружности, лежащей в плоскости, параллельной фронтальной плоскости. Эта проекция представляет собой заданную окружность без искажений. Параметры эллипсов, представляющих собой проекции окружностей, лежащих в координатных плоскостях, приведены

Рис. 2.33. Положение аксонометрических осей: а — изометрии; днметрии; в — косоугольная фронтальная диметрня

Рис. 2.34. Аксонометрические проекции окружностей

в табл. 2.3. Следует заметить, что размеры диаметров эллипсов, параллельных координатным осям, равны диаметрам заданных окружностей.

Чаще всего аксонометрические проекции применяются для построения наглядных изображений деталей. Но возможны случаи, когда в целях усиления наглядности изображение сборочной единицы строится в аксонометрической проекции (рис. 2.35).

Для показа внутренних форм предмета в аксонометрических проекциях используют разрезы. Чаще всего плоскости разреза совпадают с главными плоскостями симметрии (рис. 2.35). В аксонометрических проекциях, как правило, не применяют полных разрезов, не пользуются теми условностями, которые применяют в комплексных чертежах. Линии штриховки сечений наносят параллельно диагоналям квадратов, лежащих в соответствующих плоскостях проекций. При нанесении размеров выносные линии проводят параллельно аксонометрическим осям, размерные линии — параллельно измеряемому отрезку.

Аксонометрические изображения являются самыми простыми из наглядных изображений, применяемых в технике, и используются достаточно широко. Но метод параллельного проецирования, который используется при построении аксонометрических проекций, не позволяет строить изображения предметов такими, как мы их видим в действительности. Метод параллельного проецирования не учитывает следующие основные законы зрения человека:

1) равные между собой расстояния при удалении от наблюдателя, кажутся уменьшающимися;

2) параллельные линии сходятся в одной точке.

Построить изображение предметов с учетом этих зрительных законов можно, использовав метод центрального проецирования, при котором все проецирующие прямые

Таблица 2.3. (см. скан) Окружности в аксонометрических проекциях

Рис. 2.35. (см. скан) Разрезы в аксонометрии

пересекаются в одной точке, называемой центром проецирования.

Сущность метода центрального проецирования представлена на рис. 2.36. Проецирующие прямые выходят из центра проецирования Изображение предмета строится на плоскости К, которая носит название картинной плоскости. Изображение предмета, построенное по методу центрального проецирования с учетом отмеченных выше законов зрения, носит название перспективного изображения, или, просто, перспективы. Часто перспективой называют метод построения изображений на картинной плоскости в соответствии с теми кажущимися сокращениями размеров и изменениями очертаний формы, которые наблюдаются в действительности.

Чтобы построить перспективу предмета, необходимо иметь две его проекции (рис. 2.37, а,б). На горизонтальной проекции (рис. 2.37,б) выбирается положение центра

Рис. 2.36. Метод центрального проецирования

проецирования и положение картинной плоскости К. Наиболее выразительным и естественным перспективное изображение бывает, если угол зрения а выбирается в пределах На фронтальной проекции (рис. 2.37,а) намечается высота линии горизонта Из центра проецирования проводим через характерные точки горизонтальной проекции проецирующие прямые и определяем проекции этих характерных точек на картинной плоскости. Далее находим точки схода параллельных прямых поперечного и продольного направлений, проводя из точки прямые, параллельные соответствующим сторонам предмета на горизонтальной проекции. Полученные точки используются при построении перспективы предмета (рис. 2.37, в). От положения картинной плоскости и линии горизонта зависит видимая форма предмета.

Сравнение различных изображений однбго и гого же предмета комплексного чертежа (см. рис. 2.21, 2.25), аксонометрических проекций (см. рис. 2.32) и перспективы (рис. 2.37) говорит о преимуществах и недостатках того или иного изображения. Комплексный чертеж дает полную информацию о форме и размерах предмета, однако изображение не является наглядным. Перспективное изображение является наиболее натуральным из всех видов изображений, но размеры предмета на

Рис. 2.38. (см. скан) Перспектива тепловой электростанции

Рис. 2.39. (см. скан) Перспектива здания приборостроительного завода

чертеже являются искаженными. Аксонометрические наглядные изображения являются более простыми для построения, чем перспективные изображения.

Наиболее широко перспектива используется в строительных и архитектурных чертежах, где изображаемые предметы имеют значительную протяженность в пространстве и изображение зданнй и сооружений на чертежах должно соответствовать восприятию их глазом человека.

Иллюстративный материал архитектурно-строительной документации включает в себя чертежи, в которых изображения, построенные в линейной графике, дополняются передачей светотени, фактуры материалов здания (рис. 2.38, 2.39). Для усиления

Рис. 2.40. (см. скан) Перспектива здания научно-исследовательского института

реальности изображения здания дополняются окружающими их предметами: соседней застройкой, растительностью, людьми и т. д. (рис. 2.40).

Источник

Наглядные пособия, их роль в использовании при изучении нового материала по математике

План работы:

1. Значение наглядности и её применение на уроках математики в начальных классах.

3. Изготовление наглядных пособий учащимися.

5. Список использованной литературы.

1. Введение.

Математика изучает не сами предметы и явления окружающей жизни, а “ пространственные формы и количественные отношения действительного мира” ( Ф. Энгельс), поэтому при обучении математике стремятся вычленить именно эти стороны; качественные же признаки предметов становятся несущественными. Часто для изучения математических соотношений и операций используют специально созданные пособия. Такие пособия иногда являются более наглядными, чем сами предметы или ситуации, взятые из окружающей жизни.

На уроках математики осуществляются во взаимосвязи все основные принципы обучения: сознательность, наглядность, систематичность, прочность, учет возрастных возможностей, индивидуальный подход. В обучении математике особую роль играет принцип наглядности.

Несомненно, учебник является основным средством обучения. В настоящее время широко применяется, и хорошо себя зарекомендовали альтернативные учебники М.И. Моро, Л.В. Занкова, Н. Я. Виленкина и других авторов. Школа сама выбирает, какой методике отдать предпочтение, какой автор больше других подходит к их разработанной системе обучения математике.

Цель моей работы: узнать, что такое наглядные пособия, их виды. Научиться правильно подбирать и применять их, овладеть умением самому изготовлять необходимое наглядное пособие.

Правильное использование наглядности на уроках математики способствует формированию четких пространственных и количественных представлений, содержательных понятий, развивает логическое мышление и речь, помогает на основе рассмотрения и анализа конкретных явлений прийти к обобщению, которые затем применяются на практике.

2.Значение наглядности и применение на уроках математики в начальных классах.

Применение различных средств наглядности активизирует учащихся, возбуждает их внимание и тем самым помогает их развитию, способствует более прочному усвоению материала, дает возможность экономить время. Тот факт, что математике присуща большая абстрактность, определяет и характер средств наглядности, и особенности применения их. В таких учебных предметах, как естествознание, история, география, наглядные пособия чаще всего используются для показа изучаемых объектов. Чтобы учащиеся могли составить наиболее правильное, наиболее полное представление о животном или растении, о том или ином событии, о природном явлении и т.п., все это необходимо показать в возможно более естественном виде и так, чтобы хорошо были различимы все нужные детали.

3. Виды наглядных пособий, используемых в начальном обучении математике.

Разумеется, это деление в какой – то мере условно.

К познавательным таблицам относятся такие, которые содержат в себе новые сведения и поэтому чаще всего используются при объяснении нового материала. К их помощи можно прибегать также при повторении с целью расширения и обобщения знаний учащихся. Примером познавательных таблиц может служить нумерационная таблица, показывающая разряды и классы счетных единиц, изготавливаемая в соединении с наборным полотном. В таком виде она используется и как тренировочная. Познавательным таблицам относится также серия таблиц “ Измерение длины”, “ Измерение веса”, “ Измерение площади”, которые дают наглядное представление об основных мерах и содержат единичные отношения их, и ряд других.

Инструктивные таблицы в наглядной форме дают указания по выполнению тех или иных действий, связанных с формированием навыков написания цифр, решения задач, вычислительных навыков. К этим таблицам относятся таблицы с образцами рукописных цифр, с примерами, указывающими порядок выполнения арифметических действий, с примерами алгоритмов действий и др. такие таблицы вывешиваются в классе на более или менее продолжительное время, чтобы они помогали учащимся в их работе, давали необходимые указания.

Тренировочные таблицы предназначаются для проведения многократных упражнений, с целью формирования вычислительных навыков. Наиболее известными из таких таблиц являются таблицы для устных вычислений. Эти таблицы освобождают учителя от необходимости выписывать длинные ряды чисел и тем самым облегчают его работу и позволяют экономить время.

а) предметный дидактический материал;

б) дидактический материал в виде карточек с математическими заданиями.

К предметному дидактическому материалу относятся: счетные палочки, наборы разнообразных геометрических фигур, модели монет и т. п. Предметный материал необходимо использовать как при объяснении новых знаний, так и при их закреплении.

Дидактический материал в виде карточек с математическими заданиями обеспечивает приспособление к индивидуальным особенностям учащихся. Некоторые виды карточек позволяют освободить учащихся от переписывания заданий, что дает возможность выполнить больше упражнений.

Изготовление наглядных пособий учащимися.

Многие наглядные пособия – таблицы, некоторые модели, абаки для индивидуального пользования, палетки, счетный материал, некоторые виды раздаточного материала и т. п. – могут быть сделаны самими учащимися. При изготовлении того или иного пособия, у учащихся неизбежно возникает интерес к нему, появляется желание разобраться в его назначении и математической структуре. А это приводит к лучшему пониманию и лучшему усвоению учебного материала. В ходе работы по изготовлению пособий осуществляются межпредметные связи: с одной стороны, дети применяют свои математические знания и навыки ( расчет, измерение, черчение). А с другой- они опираются на навыки, приобретенные на уроках труда( вырезание из бумаги, склеивание и др.)

Приведем примеры наглядных самодельных пособий, которые могут быть выполнены учащимися, и дадим краткое описание способов их изготовления. Все пособия выполняются под руководством или по указанию учителя.

1. Раздаточный материал в виде геометрических фигур, звездочек, рисунков листьев и других предметов может быть изготовлен на листках бумаги или из картона. Для размножения рисунка применяются картонные трафареты или штампы, вырезаемые из сырой картофелины или резины.

Правила игры в домино и лото с картинками обычные. Дети не только учатся считать, но и соотносить между собой численности множеств, состоящих из различных предметов.

3.Абак для индивидуального пользования. Изготавливается из небольшого куска плотной бумаги, разлинованного на три колонки соответственно трем первым числовым разрядам. В каждой колонке прорезается по 10 круглых или квадратных отверстий. Снизу подшивается или подклеивается цветная бумага, чтобы хорошо были видны на фоне ее вырезанные отверстия. Подшитая бумага должна быть, таким образом, чтобы под каждым рядом отверстий оставался небольшой промежуток для узкой картонной полоски. Выдвигая полоски, учащиеся в каждом разряде открывают нужное число отверстий и тем самым показывают заданное многозначное число.

4. Модель циферблата с подвижными стрелками. Деления на круге должны быть нанесены достаточно точно, чтобы учащиеся могли определять показания часов.

6. Демонстрационные таблицы, схемы, диаграммы.

Для изготовления таких пособий следует широко использовать рисунки из старых книг, журналов, календарей, наклеивая их на большие листы бумаги и дополняя необходимыми линиями и числами. Цифры для изображения чисел могут быть вырезаны из старых перекидных или отрывных календарей.

Заключение.

Знание видов наглядных пособий дает возможность правильно их подбирать и эффективно использовать при обучении. А также изготовлять самому или вместе с детьми необходимые наглядные пособия. Наглядные учебные пособия принято делить на натуральные и изобразительные. К натуральным наглядным пособиям,, используемым на уроках математики, относятся предметы окружающей среды. Среди наглядных изобразительных пособий выделяют образные: предметные картинки, изображения предметов и фигур из бумаги и картона, таблицы с изображениями предметов или фигур. К изобразительным наглядным относятся также наглядные экранные пособия, учебные фильмы, диафильмы, диапозитивы.

С точки зрения использования наглядные пособия делят на общеклассные и индивидуальные.

К изготовлению наглядных пособий полезно привлекать детей. Это имеет большое образовательное и воспитательное значение, содействует сознательному и прочному овладению знаниями и умениями, помогает выработке определенных трудовых навыков. Так, изготовляя модель прямого угла из бумаги и модель подвижного угла из двух палочек, скрепленных куском пластилина, ученики получают представление об углах; изготовляя модели линейного и квадратного сантиметра, дециметра, метра, учащиеся получают наглядное представление о единицах длины и площади. Работая с пособиями, изготовленными своими руками, ребенок учится уважительно относиться к труду.

В процессе обучения наглядные пособия используют с различными целями: для ознакомления с новым материалом, для закрепления знаний, умений, навыков, для проверки их усвоения.

Знакомя с новым материалом, нужно использовать наглядное пособие с целью конкретизации сообщаемых знаний. В этом случае наглядное пособие выступает как иллюстрация словесных объяснений.

Например. Помогая детям в поисках решения задачи, нужно сделать схематический рисунок или чертеж к задаче; объясняя прием вычисления, сопровождая пояснение действиями с предметами и соответствующими записями и т. д. При этом важно использовать наглядное пособие своевременно, иллюстрируя самую суть объяснения, привлекая к работе с пособием и пояснению самих учащихся. При раскрытии приема вычисления, измерения, решении задачи и т. д. надо особенно четко показывать движение ( прибавить- придвинуть, вычесть – убрать, отодвинуть). Сопровождение объяснения рисунком (чертежом) и математическими записями на доске не только облегчает детям восприятие материала, но и одновременно показывает образец выполнения работы в тетрадях. Например: как расположить чертеж и запись решения в тетради, как обозначить периметр с помощью букв и т. п.

При ознакомлении с новым материалом и особенно при закреплении знаний и умений надо так организовать работу с наглядными пособиями, чтобы учащиеся сами оперировали ими и сопровождали действия соответствующими пояснениями : объединяли множества предметов при изучении сложении, моделировали замкнутые и ломаные незамкнутые линии, пользуясь палочками.

Качество усвоения материала в большинстве случаев значительно повышается, так как в работу включаются различные анализаторы( зрительные, двигательные, речевые, слуховые). При этом дети овладевают не только математическими знаниями. Но и приобретают умения самостоятельно использовать наглядные пособия. Учитель должен всячески поощрять детей к использованию наглядных средств, к самостоятельной работе.

На этапе закрепления знаний и умений необходимо широко использовать для разнообразных упражнений справочные таблицы, таблицы для устного счета, рисунки, схемы, чертежи для составления задач детьми. Для выработки измерительных навыков нужно включать упражнения в черчении и измерении с помощью чертежно- измерительных инструментов. Рекомендуется практиковать ВОСПРОИЗВЕДЕНИЕ НАГЛЯДНО ВОСПРИНЯТОГО ПУТЕМ МОДЕЛИРОВАНИЯ, РИСОВАНИЯ, СЛОВЕСНОГО ОПИСАНИЯ.

Наглядные пособия иногда используют для проверки знаний и умений учащихся. Это делается так: – чтобы проверить, как усвоили дети понятие многоугольник, можно предложить с помощью палочек сложить многоугольник указанного вида. Используя раздаточный дидактический материал, учитель проверяет умения измерять длину отрезков, площадь, периметр многоугольников и др.

Важным условием эффективности использования наглядных пособий является применение на уроке достаточного и необходимого количества наглядного материала. Если наглядные средства применять там, где этого совсем не требуется, то они играют отрицательную роль, уводя детей в сторону от поставленной задачи. Подобные факты встречаются в практике: например, первоклассник обучается выбору арифметического действия при решении арифметических задач. Если привлечь для этой цели картинку, на которой нарисованы птички, сидящие на ветке и подлетающие к ним, ученик, глядя на эту картинку, находит ответ задачи простым пересчитыванием, не выполняя никакого арифметического действия над числами. Наглядность, использованная в этом случае, не только не помогает, но наоборот, задерживает формирование умения решать задачи, т. е. выбирать действие над числами, данными в условии.

Источник