Для чего нужны уравнения в жизни человека
Для чего нужны уравнения в жизни человека
Вот пример прямой задачи: сколько весит кусок сплава, на изготовление которого пошло 0,6 дм³ меди (уд. вес 8,9 кг / дм³) и 0,4 дм³ цинка (уд. вес 7,0 кг/ дм³)? При ее решении мы находим вес взятой меди (8,9 · 0,6 = 5,34 (кг)), затем вес цинка (7,0 · 0,4 = 2,8 (кг)) и, наконец, вес сплава (5,34 + 2,8 = 8,14 (кг)). Выполняемые действия и их последовательность диктуются самим условием задачи.
Вот пример косвенной задачи: кусок сплава меди и цинка объемом в 1 дм³ весит 8,14 кг. Найти объемные количества меди и цинка в этом сплаве. Здесь из условия задачи не видно, какие действия ведут к ее решению. При так называемом арифметическом решении нужно проявить подчас большую изобретательность, чтобы наметить план решения косвенной задачи. Каждая новая задача требует создания нового плана. Труд вычислителя затрачивается нерационально. Для рационализации вычислительного процесса и был создан метод уравнений, который является основным предметом изучения в алгебре. Суть этого метода такова.
1.Искомые величины получают особые наименования. Мы пользуемся для этой цели буквенными знаками (предпочтительно последними буквами латинского алфавита х, у, z, u, v). Условие задачи с помощью этих знаков и знаков действий (+, — и т. д.) «переводится на математический язык», т. е. связи между данными и искомыми величинами мы выражаем не словами и фразами разговорного языка, а математическими знаками. Каждая такая «математическая фраза» и есть уравнение.
2.После этого мы решаем уравнение, т. е. находим значения искомых неизвестных величин. Решение уравнения производится совершенно механически, по общим правилам. Нам не приходится больше учитывать особенности данной задачи; мы только должны применять раз навсегда установленные правила и приемы. (Выводом этих правил и занимается в первую очередь алгебра.)
Таким образом, уравнения нужны для того, чтобы механизировать труд вычислителя. После того как уравнение составлено, решение его можно получить вполне автоматически (в настоящее время сконструирован ряд таких автоматов). Вся трудность решения задачи сводится лишь к составлению уравнения.
«Уравнения в нашей жизни» 7 класс
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Урок « Уравнения в нашей жизни» 5 урок в теме. Число : 5.12.2007г.
Тип: урок контроля и коррекции знаний.
создать условия для проверки уровня обученности по теме «Уравнения», определить методику коррекции учебной деятельности учащихся.
развивать информационную, коммуникативную, рефлексивную компетентности
воспитывать умение оценивать себя.
Оборудование : карточки с уравнениями, алгоритм решения уравнений, схема решения уравнений, лист с правильными ответами, лист о словами поэта Чосера.
Сегодня мне бы хотелось начать урок словами английского поэта ср. веков Чосера
Я уйму всяких разрешил проблем»
Готовятся к работе.
2. Целеполагание и мотивация.
На уроке повторим основные понятия по теме, алгоритм решения уравнения, свойства уравнения. напишем проверочную работу, которую оцените сами
Тему урока запишем в тетрадь «Уравнения в нашей жизни».Выберите каждый для себя цель на урок.
Записывают тему в тетрадь
Выбирают и записывают цель в тетрадь.
Вспомним основные понятия темы, которые нам будут нужны для работы.
Начнем работу со следующего уравнения
Решаем уравнение по алгоритму.
Перенос слагаемых из Л.Ч. в П.Ч и наоборот
Умножение и деление на одно и тоже число
Перенести слагаемые без переменной в П.Ч., поменяв при этом знак.
Привести подобные слагаемые в Л. и П. частях.
Поделить на коэффициент перед переменной обе части уравнения.
4. Проверка уровня знаний и умений.
Читают правила игры « ЛАБИРИНТ».
Выбирают уравнения и решают их.
Используя правила игры оценивают самостоятельно решение каждого уравнения.
Из учебника №№ 476, 477.
придумать игру с уравнениями
тест составить по решению уравнений.
Выбирают каждый для себя д/з. и записывают в дневник.
Что мы с вами сегодня делали?
Какие качества человека, развивает умение решать уравнения.
Достигли ли вы целей, которые поставили в начале урока, сделайте вывод.
Отвечают на вопросы, записывают вывод в тетрадь каждый по своей цели.
Усидчивость, логику, мышление, устремление, силу воли …
* я мечтаю сам решать уравнения
*я желаю сам проверять свою работу
* я хочу самостоятельно решать уравнения
*хочу находить корни уравнения
* мне интересно узнать, какими свойствами обладают уравнения
*я хочу знать, как переносятся слагаемые из одной части уравнения в другую
*мне интересно, для чего решаются уравнения
*мне очень интересно, какие качества человека развивает решение уравнений
* я мечтаю сам решать уравнения
*я желаю сам проверять свою работу
* я хочу самостоятельно решать уравнения
*хочу находить корни уравнения
* мне интересно узнать, какими свойствами обладают уравнения
*я хочу знать, как переносятся слагаемые из одной части уравнения в другую
*мне интересно, для чего решаются уравнения
*мне очень интересно, какие качества человека развивает решение уравнений
* я мечтаю сам решать уравнения
*я желаю сам проверять свою работу
* я хочу самостоятельно решать уравнения
*хочу находить корни уравнения
* мне интересно узнать, какими свойствами обладают уравнения
*я хочу знать, как переносятся слагаемые из одной части уравнения в другую
*мне интересно, для чего решаются уравнения
*мне очень интересно, какие качества человека развивает решение уравнений
* я мечтаю сам решать уравнения
*я желаю сам проверять свою работу
* я хочу самостоятельно решать уравнения
*хочу находить корни уравнения
* мне интересно узнать, какими свойствами обладают уравнения
*я хочу знать, как переносятся слагаемые из одной части уравнения в другую
*мне интересно, для чего решаются уравнения
*мне очень интересно, какие качества человека развивает решение уравнений
* я мечтаю сам решать уравнения
*я желаю сам проверять свою работу
* я хочу самостоятельно решать уравнения
*хочу находить корни уравнения
* мне интересно узнать, какими свойствами обладают уравнения
*я хочу знать, как переносятся слагаемые из одной части уравнения в другую
*мне интересно, для чего решаются уравнения
*мне очень интересно, какие качества человека развивает решение уравнений
Перенос слагаемых из Л.Ч. в П.Ч и наоборот
Умножение и деление на одно и тоже число
3.Перенести слагаемые без переменной в П.Ч., поменяв при этом знак.
4.Привести подобные слагаемые в Л. и П. частях.
5.Поделить на коэффициент перед переменной обе части уравнения.
Я уйму всяких разрешил проблем»
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: 62580040729
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В России разработают рекомендации по сопровождению студентов с ОВЗ
Время чтения: 2 минуты
Во всех педвузах страны появятся технопарки
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Зарплаты педагогов Ростовской области вырастут в среднем на 10-15%
Время чтения: 2 минуты
В России стартует пилотный проект по реабилитации детей-инвалидов
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Зачем нужны дифференциальные уравнения?
Ну и да, не сочтите за навязчивую рекламу, но это же мой пост, всё-таки.
В общем, я уже некоторое время занимаюсь репетиторством. Готовлю школьников к экзаменам, помогаю студентам освоиться в математике. Судя по отзывам, объясняю вполне себе доходчиво и интересно. А сейчас как раз в расписании появилась ещё пара мест для новых людей. Так что, если вдруг вам надо к чему-то подготовиться, что-то подтянуть, понять и т.п., обращайтесь, будем думать =Ъ
порядок изучения основ матанализа у нормальных людей:
1) теория множеств, функции и теория пределов.
2) дифференциальное и интегральное исчисление.
3) ряды
в школе:
1) функции
2) дифференциальное и интегральное исчисление
. Полезные практические знания пришли не от «теоретического трёпа», (как бы нас ни старались обмануть СТАНДАРТНЫМИ попугайскими сказками на эту тему)! «Теорию» подгоняют потом.
Вот если б мне так в школе объяснили, то я бы всё равно ничего не поняла.
Но автору плюсище за попытку обратить гуманитариев в технарей!)
Проблема простых-близнецов – Алексей Савватеев | Научпоп
В чём заключается одна из самых древних проблем «школьной» математики? Почему она называется «простые-близнецы» и как формулируется? Что утверждает теорема о распределении простых чисел в натуральном ряду? Как продвинулась в этой области современная математика и на какие вопросы ещё предстоит найти ответы математикам будущего?
Рассказывает Алексей Савватеев, математик и матэкономист, доктор физико-математических наук, научный руководитель Кавказского Математического Центра АГУ, ректор Университета Дмитрия Пожарского, профессор МФТИ, научный руководитель ЦДПО РЭШ, ведущий научный сотрудник ЦЭМИ РАН, популяризатор математики среди детей и взрослых.
Молдавские учёные решили проблему, над которой 140 лет бились математики всего мира
Два математика из Молдовы первыми в мире решили алгебраическую проблему, над которой 140 лет размышляли великие ученые мира. Об этом на этой неделе сообщил Технический университет Молдовы (UTM).
«Доктор физико-математических наук Михаил Попа и доктор математических наук Виктор Прикоп первыми в мире нашли решение знаменитой проблемы центра и фокуса, поставленной выдающимся французским математиком Анри Пуанкаре, над которой великие математики мира размышляли более века», — говорится на сайте университета.
Этой проблеме посвятили тысячи работ математики из Франции, России, Беларуссии, Китая, Великобритании, Канады, США и других стран мира. Только в Молдове число работ, посвященных проблеме Пуанкаре, приближается к сотне, отметили в UTM.
Профессор университета Михаил Попа, основатель научной школы алгебры Ли и дифференциальных систем, предложил собственное решение проблемы центра и фокуса, которое привело его к результату, ставшему открытием.
Во время исследований к профессору присоединился его ученик Виктор Прикоп. Вместе они усовершенствовали первоначальную гипотезу в монографии «Проблема центра и фокуса. Алгебраические решения и гипотезы».
Работа была переведена на английский язык и представлена для издания в несколько зарубежных издательств. В итоге лучшие условия предложил издательский дом «Taylor & Francis Group», расположенный в Великобритании и специализирующийся на публикациях научной литературы и журналов.
Где-то всплакнул Гриша Перельман.
Панорама, да не та. И с такими лицами не шутят.
Что такое наука и какие задачи она должна решать? Существует ли музыкальная наука и какими могут быть результаты применения научного метода в этой сфере? Что такое микрохроматика и как она может изменить музыку будущего, расширить возможности её создания и восприятия?
Реставрирую шкаф
Работа не быстрая, поэтому фото до. Нашел в нем тайник, в тайнике фото.
Интересует, что за формула на доске?
Пока ответа не нашлось.
Шкаф в СПБ. Ещё была найдена карта Казани печать старая начало 20 века.
Что, если наш 4D мир станет пятимерным?
Краткая текстовая версия видео:
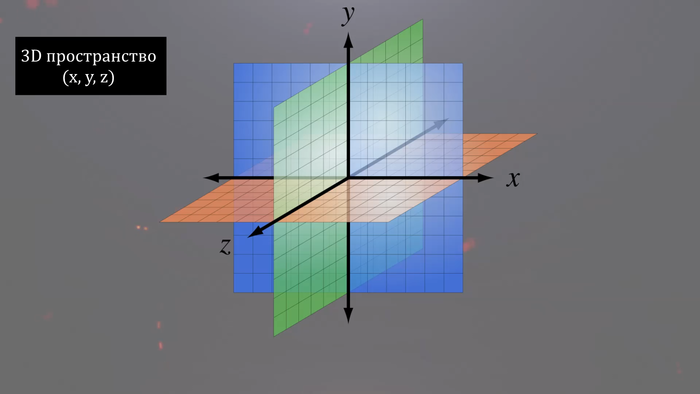
Мир, в котором мы живем, является четырехмерным. По крайней мере в макро масштабе. В нашем мире 3 пространственных измерения и одно временное. Трехмерность пространства значит, например, то, что мы можем в нем провести три взаимно перпендикулярных координатных осей расположенных под углом 90 градусов. В таком пространстве можно двигаться «влево-вправо», «вперед-назад» и «вверх-вниз».
В трехмерном пространстве мы можем завязать узел. В двумерном пространстве завязать узел невозможно. А еще в трехмерном пространстве стул может стоять только на трех ножках или больше, стул на двух ножках потеряет равновесие и упадет (Речь идет о ножках типа такого, как на фото).
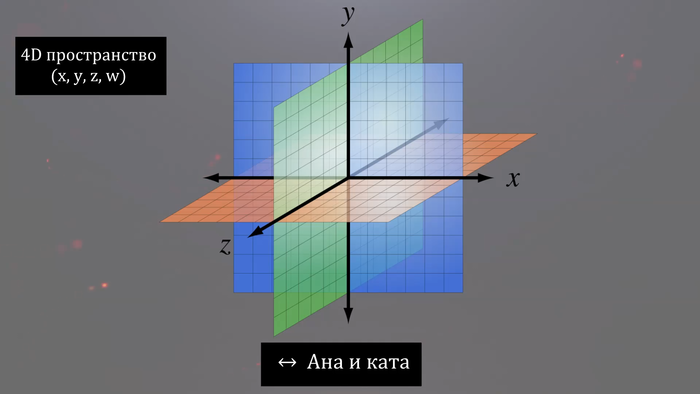
А что будет, если мы добавим еще одно пространственное измерение? То есть представим себе пятимерный мир, 4 пространственных измерения и 1 временное?
В таком мире можно провести еще одну ось перпендикулярную к остальным трем осям под углом 90 градусов. В трехмерном пространстве сделать это невозможно и как-то точно визуализировать я это не могу, так что включайте фантазию.
В пятимерном мире так же добавятся новые направления движения, которые называют «ана-ката», получается: «влево-вправо», «вперед-назад», «вверх-вниз» и «ана»-«ката». Представить себе направление движения ана и ката мы не можем, так же как существо в двумерном мире не может представить себе направления вверх и вниз.
В таком мире можно завязать двумерную сферу на узел, в нашем мире сделать это невозможно, показать, соответственно, тоже нельзя. Ну и стул с тремя ножками не сможет стоять в мире с 4 пространственными измерениями, чтобы он был устойчив потребуется 4 или больше ножек.
Ну хорошо, я понимаю, вы вряд ли Вы читаете это, чтобы узнать о узлах и ножках стула, Вас интересует, что будет с нашим миром, если внезапно в него добавить еще одно измерение, вот так по щелчку пальца «тыц» и добавили еще одно пространственное измерение и вот ты уже в 5 измерении, что с тобой будет?
Если коротко то… умрешь конечно же. А еще Земля станет приплюснутой. Сейчас расскажу как именно умрешь и почему земля станет приплюснутой.
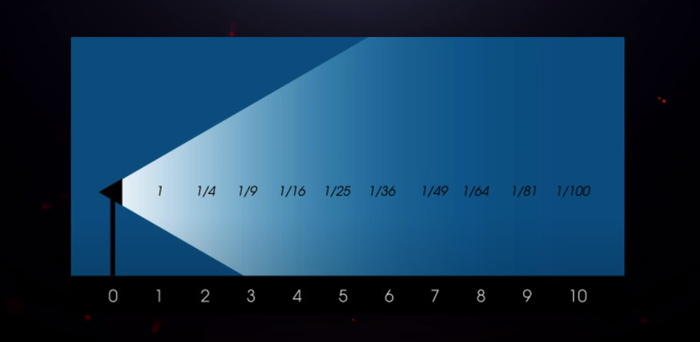
Есть такой закон – закон обратных квадратов, и он тесно связан с размерностью пространства. Возьмем для примера светящий фонарь, интенсивность света в таком случае убывает согласно закону обратных квадратов.
Объект, перемещенный на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении. На расстоянии в 3 раза большее от источника – в 9 раз меньше мощности, на расстоянии в 4 раза большее от источника – 16 раз и так далее.
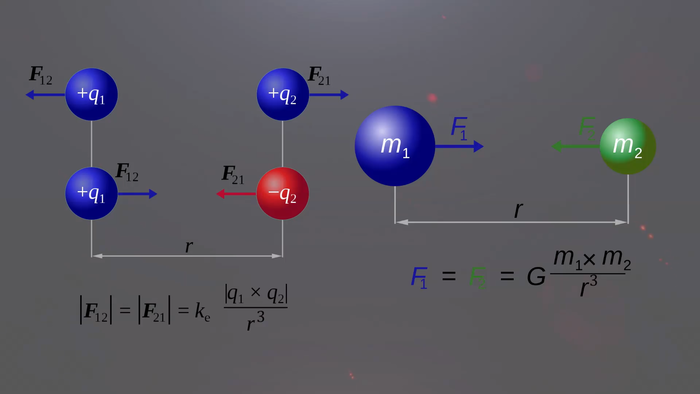
В законе всемирного тяготения сила гравитационного притяжения убывает тоже с квадратом расстояния. В два раза увеличиваем расстояние, сила притяжения уменьшается в 4 раза и так далее. Тоже самое с законом Кулона – сила притяжения или отталкивания заряженных частиц убывает с квадратом расстояния. В 5D мире закон обратных квадратов превращается в закон обратных кубов. Теперь интенсивность света будет падать не с квадратом расстояния, а с кубом расстояния. r^2 в законе Кулона и Законе всемирного тяготения превращается в r^3.
Это все полностью изменит химические элементы из которых мы состоим, некоторые атомы станут нестабильными, радиоактивными, другие наоборот, станут стабильными.
Например, в 5D мире магний был бы благородным газом, а не металлом, то есть некоторые элементы станут менее реактивными, другие более реактивными. Ионизация атомов будет осуществляться при значительно меньших энергиях, да и вообще агрегатное состояние различных элементов будет меняться не так, как в нашем мире, некоторые хим. элементы станут газообразны при комнатной температуре, некоторые затвердеют и такие вот вещи. Думаю, практически бессмысленно вспоминать биологические процессы, благодаря которым мы можем жить, ведь это все поменяется кардинально, мы мгновенно потеряем сознание и умрем, синтез белков, транспортировка различных аминокислот, нейромедиаторов, нервные импульсы, это все либо прекратится, либо изменится до неузнаваемости. Ну и конечно же спектры атомов изменятся, а это значит, что все резко поменяет цвет, что-то станет прозрачным, что-то непрозрачным, да и вообще привычные для нас источники света выглядели бы более тускло из-за r^3, с запахами та же история, правда уже некому будет смотреть и нюхать все это, ведь все живые существа погибнут.
Короче будет происходить полная жесть, что-то будет плавится, что-то превратится в газ, что-то затвердеет, некоторые вещества станут радиоактивными, привычные нам вещи потеряют свои свойства и перестанут работать так, как в нашем мире. Я напомню, что это все в мире, в котором 4 пространственных измерения и одно временное и в котором можно двигаться в направлении ана и ката. Но кроме дополнительного направления появятся также дополнительные степени свободы во вращении. В нашем мире ориентацию тела можно задать тремя углами, в быту это называется «наклон, подъём и поворот», в 5D мире надо представить себе еще 3 дополнительных степени свободы вращения перпендикулярные к 3 вышеупомянутым. Но по идее, на вращение Земли это не должно повлиять, момент импульса сохранится, ведь нужно, чтобы какая-то сила передала момент импульса Земле, чтобы она могла вращаться в какой-то непривычный для нас способ. Конечно Земля изменит свой привычный облик, из-за того, что свойства химических элементов изменятся, но из-за гравитации все должно также удерживаться вокруг центра масс, правда земля довольно быстро вращается, а так как гравитация в 5D мире у нас ослабевает с кубом расстояния, то земля сплюснется и формой будет напоминать что-то типа такого, как на картинке.
Но вообще, появится дополнительное направление, в котором могут двигаться частицы из которых состоит земля, планета начнет превращаться в гиперсферу, представить себе этот процесс, эти метаморфозы которые будут происходить, очень сложно.
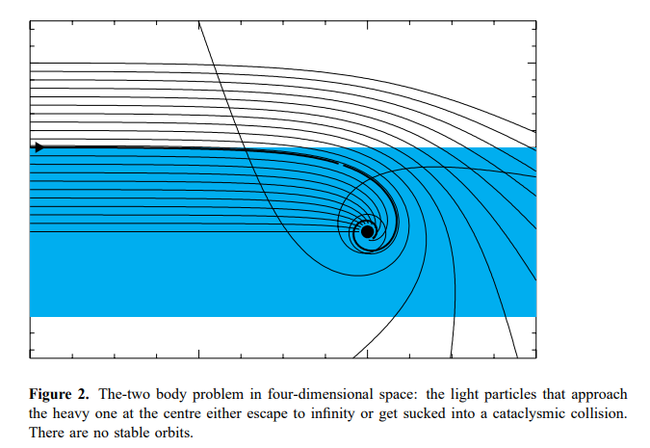
Будут ли происходить термоядерные реакции на солнце, тут под вопросом, но изменения явно произойдут. Но вот что забавно – в пятимерном мире нет стабильных орбит. Вот, посмотрите на график, это моделирование классической задачи двух тел, оказывается, что устойчивых орбит в 5D мире нет, тела либо падают друг на друга, либо улетают в бесконечность, поэтому солнечная система, как и все другие системы, разрушится, некоторые тела упадут на другие тела, а некоторые улетят бороздить просторы галактики.
Казалось бы, следуя логике как с законом обратных квадратов, все квадраты в других уравнениях тоже надо заменить на кубы и получается, что формула эквивалентности массы и энергии в пятимерном пространстве будет работать как Е=мс в кубе, но нет, эта формула, как и множество других, не изменятся в пятимерном пространстве, она, как и множество других формул, не зависит от размерности пространства.
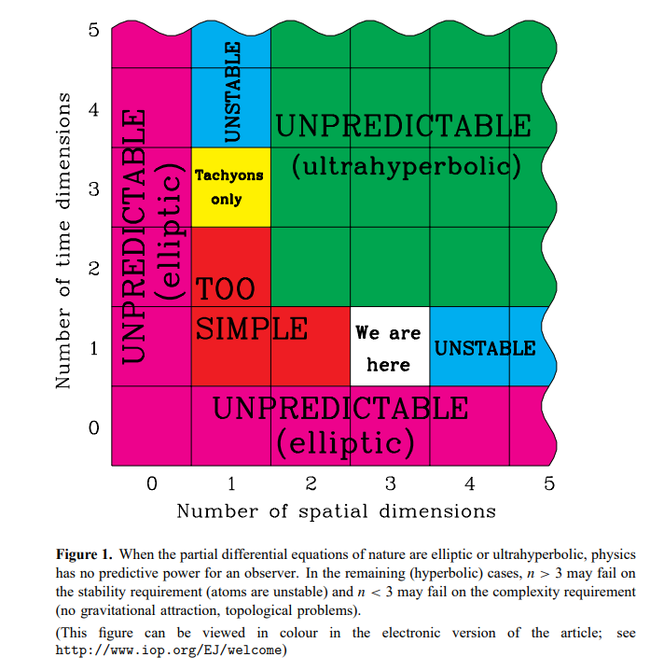
Но даже и без этого всего, мир в 5 мерном пространстве изменится настолько, что в нем не сможет существовать жизнь в том виде, в котором существует в четырехмерном пространстве. Вообще, оказывается, четырехмерный мир – самый простой из возможных и одновременно самый оптимальный для существования в нем жизни, стабильных орбит и химии, какой мы ее знаем.
Книга Кипа Торна, «Интерстеллар. Наука за кадром»