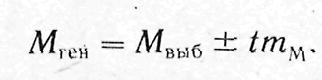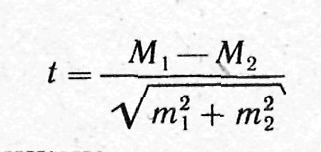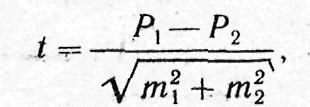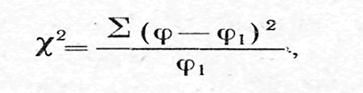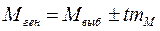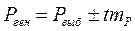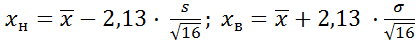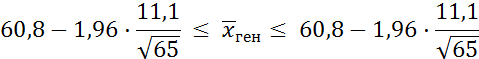Для чего определяются доверительные границы
Определение доверительных границ М и Р
Определяя для средней арифметической (или относительной) величины два крайних значения: минимально возможное и максимально возможное, находят пределы, в которых может быть искомая величина генерального параметра. Эти пределы называют доверительными границами.
Доверительные границы — границы средних (или относительных) величин, выход за пределы которых вследствие случайных колебаний имеет незначительную вероятность.
Доверительные границы средней арифметической в генеральной совокупности определяют по формуле:
Доверительные границы относительной величины в генеральной совокупности определяют по следующей формуле:
Размеры предельной ошибки (D) зависят от коэффициента t, который избирает сам исследователь, исходя из необходимости получить результат с определенной степенью точности.
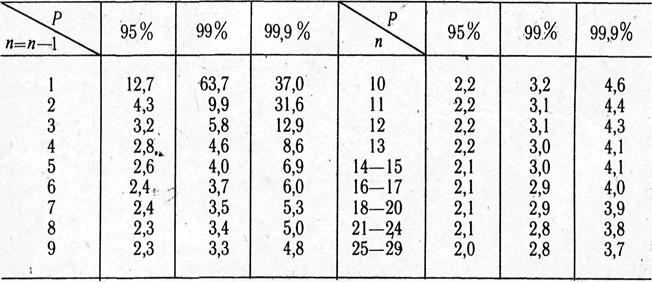
Зависимость доверительного критерия / от степени вероятности безошибочного прогноза р (при n>30)
| Степень вероятности безошибочного прогноза – P, % | Доверительный критерий t |
| 95,0 % (0,05) 99,0 % (0,01) |
Для большинства медико-биологических и социальный исследований достоверными считаются доверительные границы, установленные с вероятностью безошибочного прогноза р = 95% и более. Чтобы найти критерий t при числе наблюдений п
При определении доверительных границ сначала надо решить вопрос о том, с какой степенью вероятности безошибочного прогноза необходимо представить доверительные границы средней или относительной величины. Избрав определенную степень вероятности, соответственно этому находят величину доверительного критерия t при данном числе наблюдений. Таким образом, доверительный критерий t устанавливается заранее, при планировании исследования.
Любой параметр (средняя величина или относительная величина) может оцениваться с учетом доверительных границ, полученных при расчете.
Как видно, доверительные границы зависят от размера доверительного интервала (tm= D).
С уменьшением величины ошибки суживаются доверительные границы средних и относительных величин, полученных на выборочной совокупности, т. е. уточняются результаты исследования, которые приближаются к соответствующим величинам генеральной совокупности.
Если ошибка большая, то получают для выборочной величины большие доверительные границы, которые могут противоречить логической оценке искомой величины в генеральной совокупности.
3. Определение достоверности разности средних (или относительных) величин (по критерию t). Критерий Стьюдента. В медицине и здравоохранении по разности параметров оценивают средние и относительные величины, полученные для разных групп населения по полу, возрасту, а также групп больных и здоровых и т. д. Во всех случаях при сопоставлении двух сравниваемых величин возникает необходимость не только определить их разность, но и оценить ее достоверность.
Достоверность разности величин, полученных при выборочных исследованиях, означает, что вывод об их различии может быть перенесен на соответствующие генеральные совокупности.
Формула оценки достоверности разности сравниваемых средних величин такова:
и для относительных величин:
Для большинства исследований, проводимых в биологии, такая степень вероятности является вполне достаточной.
При величине критерия достоверности t 2 соответствие эмпирического распределения теоретическому, оценивают достоверность различия между выборочными совокупностями.
Критерий c 2 (в отличие от критерия t) применяется в тех случаях, когда нет необходимости знать величину того или иного параметра (среднюю или относительный показатель) и требуется оценить достоверность различия не только двух, но и большего числа групп.
Так, критерий соответствия c 2 может быть использован для ответа на следующие вопросы: существенно ли отличаются друг от друга группы вакцинированных и невакцинированных по распределению их на больных и здоровых (т.е. эффективна ли вакцина); существенно ли отличаются группы населения с разным среднедушевым доходом по распределению их на больных и здоровых (т.е. влияет ли материальное обеспечение на уровень заболеваемости) и т. д.
Критерийc 2 (хи-квадрат) определяется по формуле:
Такой принцип доказательства «от противного» является довольно распространенным во многих исследованиях и применяется при расчете критерия c 2
Последовательность расчета критерия на примере.
Требуется оценить при помощи критерия c 2 различаются ли по срокам заболеваемости корью группа вакцинированных и невакцинированных лиц (до вакцинации и после вакцинации).
Этапы расчета представлены в табл.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Определение доверительных границ генеральной совокупности.



Определяя для средней арифметической (или относительной) величины два крайних значения: минимально возможное и максимально возможное, находят пределы, в которых может быть искомая величина генерального параметра. Эти пределы называют доверительными границами.
Доверительные границы — это то максимальное и минимальное значение, в пределах которого, при заданной степени вероятности безошибочного прогноза, может колебаться искомая средняя величина генерального параметра.
Доверительные границы средней арифметической в генеральной совокупности определяют по формуле:
Доверительные границы относительной величины в генеральной совокупности определяют по следующей формуле:
где Мген и Pген — значения средней и относительной величин, полученных для генеральной совокупности; Мвыб и Рвыб —значения средней и относительной величин, полученных для выборочной совокупности; mM и mР — ошибки репрезентативности выборочных величин; t — доверительный критерий (критерий точности, который устанавливают при планировании исследования; tm — доверительный интервал; tm=Δ, где Δ предельная ошибка показателя, полученного при выборочном исследовании.
Размеры предельной ошибки (Δ) зависят от коэффициента t, который избирает сам исследователь, исходя из необходимости получить результат с определенной степенью точности.
Величина критерия t связана определенными отношениями с вероятностью безошибочного прогноза — р и численностью наблюдений в выборочной совокупности.
Зависимость доверительного критерия t от степени вероятности
безошибочного прогноза (при n>30)
| Степень вероятности безошибочного прогноза в % | Доверительный критерий —t |
| 95,0 | |
| 99,0 |
Для большинства медико-биологических и социальных исследований достоверными считаются доверительные границы, установленные с вероятностью безошибочного прогноза р = 95% и более. Чтобы найти критерий t при числе наблюдений n
Любой параметр (средняя величина или относительная величина) может оцениваться с учетом доверительных границ, полученных при расчете.
Для ознакомления с методикой определения доверительных границ Мвыб и Рвыб рекомендуется записать исходные данные и провести расчеты в определенной логической последовательности:
Пример 1. Определить доверительные границы среднего уровня пепсина у больных гипертиреозом с 95% вероятностью безошибочного прогноза (р = 95%).
Условие задачи: n=49
р = 95% (следовательно при n = 49 t = 2).
Определяем доверительные границы средней величины в генеральной совокупности.
Решение : Мген = 1 г% ± 2 х 0,05 г%
Мген не более 1 г% +0,1 г% = 1,1 г%,
Мген не менее 1 г%—0,1 г% =0,9 г%.
Вывод: Установлено с вероятностью безошибочного прогноза (р = 95%>, что средний уровень пепсина в генеральной совокупности у больных с гипертиреозом не превышает 1,1 г% и не ниже 0,9 г%.
Пример 2. Определить доверительные границы показателя частоты дистрофии пародонта у больных с абсцессом легкого с вероятностью безошибочного прогноза р = 95%.
р =95% (следовательно, при n=110 t=2).
Определяем доверительные границы относительного показателя в генеральной совокупности.
Решение: Рген = 49% ±2 х 4,7%
Рген не более 40% + 9,4 = 49,4%
Рген не менее 40% –9,4 = 30,6%
Вывод: Установлено с 95% вероятностью безошибочного прогноза (р = 95%), что дистрофические изменения пародонта в генеральной совокупности наблюдаются у больных с абсцессом легкого не чаще, чем в 49,4%, и не реже, чем в 30,6% случаев.
Как видно, доверительные границы зависят от размера доверительного интервала (tm=Δ).
Анализ доверительных интервалов указывает, что при заданных степенях вероятности (р) и n ≥30 t имеет неизменную величину и при этом доверительный интервал зависит от величины ошибки репрезентативности (mм или mР).
С уменьшением величины ошибки суживаются доверительные границы средних и относительных величин, полученных на выборочной совокупности, т. е. уточняются результаты исследования, которые приближаются к соответствующим величинам генеральной совокупности.
Если ошибка большая, то получают для выборочной величины большие доверительные границы, которые могут противоречить логической оценке искомой величины в генеральной совокупности.
Например, при определенном режиме питания и тренировок спортсменов средняя годовая прибавка массы тела у 80 спортсменов составила Мвыб=1 кг; mM= ±0,8 кг. При степени вероятности р = 95,0% и t = 2 Мген = 1 кг ± 2 х 0,8 кг. Следовательно:
Мген не более + 2,6 кг,
Мген не менее – 0,6 кг.
Эти противоречивые данные означают, что при указанном режиме спортсмены могут дать большую среднюю прибавку массы тела (до +2,6 кг), но могут и убавить массу тела в среднем на 600 г. Таким образом, остается по-прежнему невыясненным вопрос о степени влияния данного режима спортсменов на массу их тела.
В подобном случае надо искать резервы сокращения размаха доверительных границ в размере величины ошибки репрезентативности. Прежде всего надо проанализировать уровень разнообразия признака по среднему квадратическому отклонению (σ) с позиций однородности группы. Необходимо также иметь в виду, что большое влияние на величину средней ошибки, а следовательно, и на доверительные границы оказывает численность наблюдений.
Доверительные границы Мвыб и Рвыб зависят не только от средних ошибок этих величин (mM или mР), но и от избранной исследователем степени вероятности безошибочного прогноза (р). При большой степени вероятности размах доверительных границ увеличивается.
Что включает в себя оценка достоверности результатов исследования выборочной совокупности?
1. Расчет ошибки репрезентативности средней арифметической.
2. Расчет доверительных границ средних величин.
3. Расчет достоверности разности средних величин.
4. Расчет ошибки репрезентативности относительных величин.
5. Расчет доверительных границ относительных величин.
6. Расчет достоверности разности относительных величин.
Что характеризует ошибка репрезентативности?
1. Расхождение между числовыми характеристиками выборочной и генеральной совокупностей.
2. Насколько результаты выборочного исследования отличаются от результатов, которые могут быть получены при сплошном исследовании.
3. Погрешность, допущенная при математических расчетах.
От чего зависит величина ошибки репрезентативности?
1. От числа наблюдений.
2. От степени одноpодности pяда.
3. От величины числового значения изучаемого пpизнака.
Для чего определяются доверительные границы?
1. Для вычисления средней арифметической выборочной совокупности.
2. Для определения диапазона, в котором находится средняя арифметическая, или относительная величина генеральной совокупности.
3. Для определения критерия достоверности (t).
4. Для определения ошибки репрезентативности.
5. Для определения уровня вероятности безошибочного прогноза.
Каким образом определяется уровень вероятности безошибочного прогноза?
2. Задается в зависимости от условий исследования.
3. Используется как константа.
5. Не имеет значения.
7.Какому значению критерия достоверности (t) соответствует уровень вероятности безошибочного прогноза равный 95%?
8.Какому значению критерия достоверности (t) соответствует уровень вероятности безошибочного прогноза равный 99%?
9.Какому значению критерия достоверности (t) соответствует уровень вероятности безошибочного прогноза равный 99,9%?
Что из перечисленного используется для оценки достоверности производных величин?
1. Среднее квадратическое отклонение (б)
2. Доверительный коэффициент (t)
3. Число наблюдений (n)
5. Средняя ошибка (m)
Укажите, что из перечисленного влияет на достоверность статистических данных?
1. Число наблюдений (n)
3. Вероятность безошибочного пpогноза (Ро)
4. Ошибка репрезентативности (m)
Укажите значения критерия достоверности, когда различие между производными величинами существенно.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 1. Используя приведенные данные, определите доверительные границы средней величины и достоверность, если при изучении успеваемости студентов медицинского института (не работающих – 62 студента и сочетающих учебу с работой – 47 студентов), были получены следующие данные: у неработающих: средний балл (M1) = 4,1; (mм1 = ± 0,09); у сочетающих учебу с работой: средний балл (М2) = 3,65 (mм2 = ± 0,05). Вероятность безошибочного прогноза 95%
Задача 2.Определите достоверность, если при изучении трудоспособности больных, перенесших инфаркт миокарда при наличии гипертонической болезни (83 человека) и без нее (79 человек), были получены следующие данные: число лиц, возвратившихся к труду, перенесших инфаркт миокарда с гипертонической болезнью (Р1), равно 61,0% (mр1 = ± 4,0%), без гипертонической болезни (Р2) равно 75,0% (mр2 = ± 3,0%). Вероятность безошибочного прогноза 95%.
Раздел V
Динамические ряды
Динамическим рядом называется совокупность однородных статистических величин, показывающих изменение явления на протяжении определенного промежутка времени.
Числа, из которых состоит динамический ряд, называют уровнямиряда. Уровень – это элемент динамического ряда.
Различают три основных типа динамических рядов в зависимости от составляющих его величин:
1.Динамические ряды, построенные из абсолютных величин (например, численность населения в различные годы) – простой динамический ряд.
Динамические ряды в зависимости от сроков, которые они отражают, делятся на: моментные и интервальные.
Анализ динамического ряда определяется показателями, характеризующими интенсивность его изменений и называемыми коэффициентами динамики к которым относятся:
4) Для анализа динамического ряда используются также показатели наглядности, хотя следует помнить, что для коэффициента наглядности не обязательны взаимосвязанные динамические изменения.
Динамика рождаемости населения Н-ской области
Расчет показателей динамического ряда:
2) Темп прироста: 0,2 : 7,7 · 100% = 2,6 %
3) Темп роста: 7,9 : 7,7 · 100% = 102,6%
7,8 : 7,9 · 100% = 98,7 % и т.д.
4) Показатель наглядности: уровень 2000 г. принимаем за 100%
7,9 : 7,7 ·100% = 102,6 %
7,8 : 7,7 · 100% = 101,3 % и т.д.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Дайте определение динамического ряда.
2.Назовите виды динамических рядов.
3.Из каких величин построен простой динамический ряд?
4.Из каких величин построен сложный динамический ряд?
5.Какие динамические ряды можно отнести к моментным рядам?
6.Какие динамические ряды можно отнести интервальным рядам?
7. Назовите показатели анализа динамического ряда.
Проект Extra.im
Вероятность попадания средней или относительной величины в доверительный интервал называется доверительной вероятностью.
Доверительные границы средней арифметической генеральной совокупности определяют по формуле:
Доверительные границы относительной величины в генеральной совокупности определяют по следующей формуле:
Рген = Рвыб ± t · mр
Где: Мген и Рген — значения средней и относительной величин, полученных для генеральной совокупности;
Мвыб и Рвыб — значения средней и относительной величин, полученных для выборочной совокупности;
mM и mр— ошибки репрезентативности выборочных величин;
t — доверительный критерий, который зависит от величины безошибочного прогноза, устанавливаемого при планировании исследования.
Произведение t · m (Δ) — предельная ошибка показателя, полученного при данном выборочном исследовании.
Размеры предельной ошибки зависят от коэффициента t, который избирает сам исследователь, исходя из заданной вероятности безошибочного прогноза.
Величина критерия t связана с вероятностью безошибочного прогноза (Р) и числом наблюдений в выборочной совокупности (табл. 4.1).
Таблица 4.1. Зависимость доверительного критерия t от степени вероятности безошибочного прогноза Р (при n > 30)
| Степень вероятности безошибочного прогноза (Р %) | Доверительный критерий t |
| 95,0 | |
| 99,0 | 2,6 |
| 99,9 | 3,3 |
Для большинства медико-биологических и социальных исследований достоверными считаются доверительные границы, установленные с вероятностью безошибочного прогноза = 95% и более.
Чтобы найти критерий t при числе наблюдений (n) 30 — t имеет неизменную величину и при этом доверительный интервал зависит от величины ошибки репрезентативности.
С уменьшением величины ошибки суживаются доверительные границы средних и относительных величин, полученных на выборочной совокупности, т.е. уточняются результаты исследования, которые приближаются к соответствующим величинам генеральной совокупности. Если ошибка большая, то получают для выборочной величины большие доверительные границы, которые могут противоречить логической оценке искомой величины в генеральной совокупности. В подобном случае надо искать резервы сокращения размаха доверительных границ в размере величины ошибки репрезентативности.
Доверительные границы Мвыб и Рвыб зависят не только от средних ошибок этих величин, но и от избранной исследователем степени вероятности безошибочного прогноза. При большой степени вероятности размах доверительных границ увеличивается.
3. Определение достоверности разности средних (или относительных) величин (по критерию t — Стъюдента).
В медицине и здравоохранении по разности параметров оценивают средние и относительные величины, полученные для разных групп населения по полу, возрасту, а также групп больных и здоровых и т.д. Во всех случаях при сопоставлении двух сравниваемых величин возникает необходимость не только определить их разность, но и оценить ее достоверность.
Достоверность разности величин, полученных при выборочных исследованиях, означает, что вывод об их различии может быть перенесен на соответствующие генеральные совокупности.
Достоверность разности выборочной совокупности измеряется доверительным критерием, который рассчитывается по специальным формулам для средних и относительных величин.
Формула оценки достоверности разности сравниваемых средних величин:
Для относительных величин:
Где: M1; M2 ; Р1; Р2 — параметры, полученные при выборочных исследованиях;
t — критерий достоверности (Стъюдента).
Разность статистически достоверна при t ≥ 2, что соответствует вероятности безошибочного прогноза, равной 95% и более.
Для большинства исследований, проводимых в медицине и здравоохранении, такая степень вероятности является вполне достаточной.
При величине критерия достоверности t 2 + m2 2
Границы доверительного интервала
Вероятности, признанные достаточным для того, чтобы уверенно судить о генеральных параметрах на основании выборочных характеристик, называют доверительными.
Обычно, в качестве доверительных вероятностей выбирают значения 0,95; 0,99; 0,999 (их принято выражать в процентах – 95%, 99%, 99,9%). Чем выше мера ответственности, тем более высокий уровень доверительной вероятности: 99% или 99,9%.
Доверительная вероятность 0,95 (95%) считается достаточной в научных исследованиях в области физической культуры и спорта.
Интервал, в котором с заданной доверительной вероятностью находится выборочное среднее арифметическое 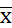
Уровень значимости оценивания – малое число α, значение которого предполагает вероятность того, что 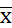
Доверительный интервал для среднего (математического ожидания) a нормального распределения:
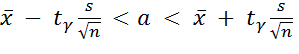
Чтобы найти границы доверительного интервала среднего значения генеральной совокупности необходимо:
1. Вычислить 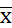
2. Следует задасться доверительной вероятностью (надежностью) γ оценивания 0,95 (95 %) или уровнем значимости α 0,05 (5 %)
3. По таблице t – распределения Стьюдента (приложение, табл. 1) найти граничные значения tγ.
4. Находим границы доверительного интервала для α = 0,05 и n = 16:
Границы доверия:
При больших объемах выборки (n ≥ 30) t – распределение Стьюдента переходит в нормальное. Поэтому доверительный интервал для 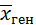
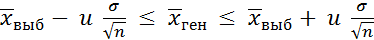
Для стандартных доверительных вероятностей (95%, 99%; 99, 9%) и уровней значимости α значения (u) приведены в таблице 8.
Значения для стандартных доверительных уровней α
| α | u |
| 0,05 | 1,96 |
| 0,01 | 2,58 |
| 0,001 | 3,28 |
1. Среднее выборочное значение 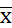
2. Задаемся доверительной вероятностью γ = 0,95 (95%);
3. Из таблицы 8 находим u0,05 = 1,96;
4. Определяем границы искомого доверительного интервала:
60,8 – 1,96·1,38 ≤ 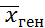
58,1 см ≤ 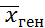
Истинное значение среднего результата прыжка вверх с места спортсменов-баскетболистов находится в интервале от 58,1 см. до 63,5 см. с доверительной вероятностью γ = 0, 95 (95%).