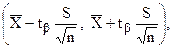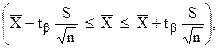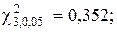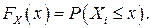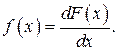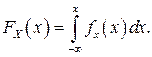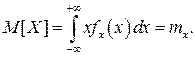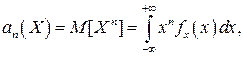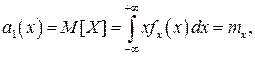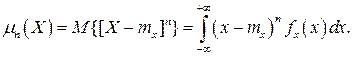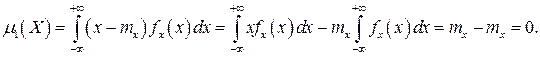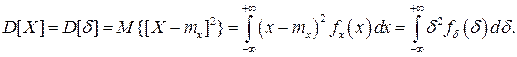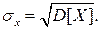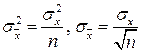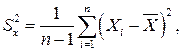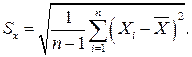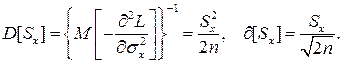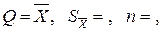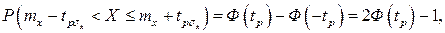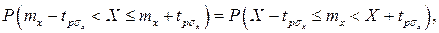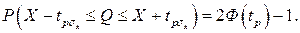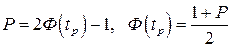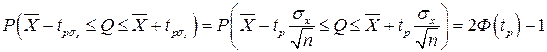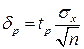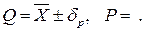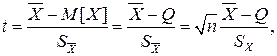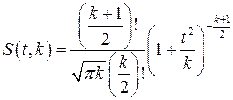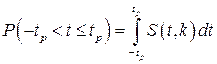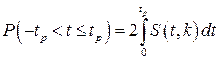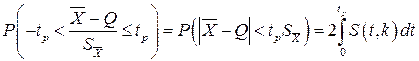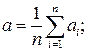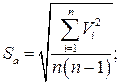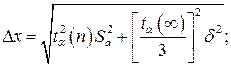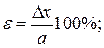Для чего строится гистограмма при оценивании погрешности многократных измерений
Обработка результатов многократных измерений
Точечная оценка результатов измерений.В практике многократных измерений наибольшее распространение получили точечные и интервальные оценки результатов измерений.
Оценку 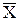
Для производственных условий наиболее характерными являются однократные измерения либо многократные измерения, причем количество многократных измерений одной и той же величины невелико (n = 5–6 измерений).
Можно говорить лишь о точечной оценке результата измерения. Число измерений невелико, поэтому отделить случайную погрешность от систематической не представляется возможным. Поскольку измерения осуществляют, как правило, в нормальных условиях, то вероятность промахов можно считать достаточно малой.
Результат измерения или среднее значение неоднократно измеряемой величины (при n = 5–6 измерений) принимается в качестве истинного, а решение о годности размера выбирают исходя из условия, что результат измерения не выходит за предел некоторой заранее заданной величины, например допуска на изготовление. При этом предельная погрешность средства измерения ±Δlim не должна превышать допускаемой погрешности измерения δ, задаваемой ГОСТ 8.051–81 в зависимости от допуска на измеряемую величину ±Δlim ≤ δ. К точечным оценкам предъявляются требования состоятельности, несмещенности и эффективности.
Оценка называется состоятельной, если при увеличении числа измерений она приближается (сходится по вероятности) к значению оцениваемого параметра, X → 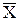
Оценка называется несмещенной, если ее математическое ожидание равно оцениваемой величине, т.е. X = 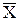
Оценка называется эффективной, когда её дисперсия является наименьшей S 2 = min.
Из теории вероятностей известно, что среднее арифметическое значение измерений является несмещенной оценкой истинного значения, а СКО среднего арифметического значения – S 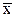
В этом случае точечная оценка результата измерения должна быть представлена в виде:
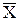
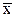
что позволяет сделать определенные, хотя и достаточно приближенные выводы о точности проведенных измерений.
Пример 3. При измерении размера вала Ø55u8 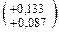
Провести точную оценку результатов измерений:

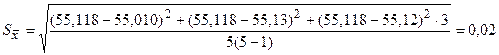
Таким образом, результат измерений
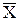
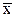
Результат измерения представляем в форме: 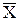
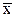
Интервальные оценки результатов наблюдений. Действительный размер – это размер, полученный в результате измерения с допустимой погрешностью измерения. Точечные оценки результатов измерения не позволяют в должной мере оценить достоверность измерения. Формулы (2.1) – (2.3) определяют статистические оценки размеров, т.е. приближенные значения их истинных величин, имеющих место в действительности. Степень приближения истинных величин, или точность каждой из оценок, определяется половиной ширины построенного для нее доверительного интервала.
Доверительным интервалом параметра X основной совокупности, т.е. совокупности всех возможных значений погрешности, называется интервал вида
где 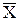
S – СКО, определяемое по формуле (2.2);
n – число измерений; tβ – коэффициент, определяемый из таблиц распределения Стьюдента при n ≤ 30 при заданной доверительной вероятности Р и k = n –1, называемым числом степеней свободы.
Результат измерений в этом случае записывается в виде:
при доверительной вероятности Р.
Значения доверительных интервалов увеличиваются с увеличением доверительной вероятности Р и уменьшаются с увеличением количества наблюдений.
Пример 4. В результате измерений вала, выполненного по Ø50b10 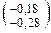
Определить доверительный интервал результатов измерений с доверительной вероятностью Р = 0,95.
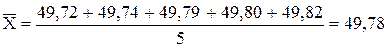
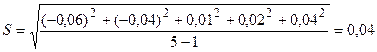
tβ = 0,27 – при k = 4, Р = 0,95.
Граница доверительного интервала
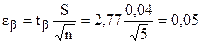
Результат измерений записывают в виде:
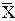
Это означает, что истинное значение измеряемого размера с вероятностью 0,95 находится в пределах от 49,73 до 49,83 мм при заданном числе измерений.
Методы проверки нормального закона распределения случайных величин. При статистической обработке результатов измерений особую роль играет проверка соответствия распределения случайных величин нормальному закону, которому чаще всего подчиняются результаты большинства случайных измерений, что необходимо для обоснованного выбора доверительных границ результатов измерений и оценки точности измерений. В наибольшей степени этой цели соответствует критерий χ 2 (критерий Пирсона).
При использовании критерия Пирсона количество измерений должно быть не менее 40.
Обычно принимается следующий порядок решения задачи.
2) Для каждого интервала подсчитывают частоты mi, равные количеству результатов, лежащих в каждом i-м интервале.
3) Определяют частость появления величин Рi* в каждом интервале:
где n – общее количество измерений, индекс «*» означает статическую оценку.
4) Находят оценку средней плотности распределения рi* случайной величины Xi в каждом интервале Δ Xi:
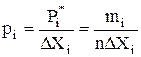
где ni – количество измерений в i – м интервале.
5) Строят гистограмму распределения величины Xi откладывая по оси абсцисс результаты наблюдений в виде интервалов Δ Xi в порядке возрастания индекса i, а по оси ординат – оценку средней плотности распределения рi, получая тем самым прямоугольник с высотой рi*.
Естественно, что площадь всех построенных прямоугольников равна единице, поскольку в нее входят все 100 % наблюдений
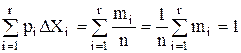
При построении гистограммы число интервалов г выбирают в зависимости от числа измерений и исходя из соотношений: при n = 40. 100 г = 7. 9, а при n = 100. 500 г = 8. 12, а масштабы по осям гистограммы рекомендуется принимать такими, чтобы отношение ее высоты к основанию составляло 5:8.
6) Соединяя середины отрезков, получают полигон распределения. Характер ломаной линии позволяет сделать предположение о виде распределения, что дает возможность с большей долей вероятности подобрать соответствующую кривую распределения.
Если СКО и математическое ожидание полигона распределения близки к значениям СКО и математическому ожиданию кривой нормального распределения, то этот вид распределения можно положить в основу гипотезы о правомерности такого предположения.
Поскольку предположение основано на результатах опытных данных случайных величин, оно должно быть подтверждено обычными методами математической статистики по критериям согласия. При числе наблюдений более 40 рекомендуется принимать критерий согласия χ 2 – Пирсона.
При этом возможны два вида ошибок: ошибка первого рода, состоящая в том, что в силу случайного характера результатов измерений отвергают верную гипотезу. Вероятность ошибки первого рода называют уровнем значимости q = 1 – α., где α – уровень доверительной вероятности, и выбирают в пределах 0,05…0,10.
Принимая неверную гипотезу, совершают ошибку второго рода, – qi, значение которой колеблется в пределах 0,95…0,9 соответственно. Физический смысл которой состоит в том, что принимают ошибочное решение о несоответствии распределения случайной величины Xi правильно выбранному теоретическому распределению.
Пример 5. При контроле размера Ø 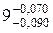
Значения величин, полученных при вычислениях, представлены в виде табл. 2.5.
По результатам расчетов строим гистограмму и полигон распределений.
Характер распределения позволяет высказать предположение о нормальном законе распределения, однако эта гипотеза должна быть проверена по критерию χ 2 – Пирсона. С этой целью:
проводят группировку данных измерений аналогично ранее описанному принципу. Если в интервале оказывается менее 5 измерений, его объединяют с соседним;
определяют среднее арифметическое значение 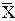
находят вероятность попадания в интервал результатов измерений по формуле
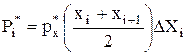
где хi и хi+1 – результаты измерений в i-м и (i +1)-м интервалах;
вычисляют величину χi 2 (i = 1, 2, …, r) для каждого интервала, затем меру расхождения χ 2 при числе степеней свободы k = r – 3.
Задавая уровень значимости q = 1 – α, значения 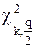
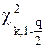
Если расчётное значение оказывается в найденных пределах – распределение результатов измерений принимают нормальным.
Пример 6. Проверить на соответствие нормальному закону полученное распределение в предыдущем примере (табл. 2.5) и представленного гистограммой (рис.2.2). Статистические характеристики наблюдений:
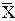
Вычисления запишем в табл. 2.6. Плотности нормированного нормального распределения Р(ti) взяты из таблицы дифференциальной функции нормированного нормального распределения, а число степеней свободы k = 8 – 2 –3 = 3, поскольку два первых и два последних интервала объединены в один (в первом и последнем частота наблюдений mi 2
Поскольку соблюдается соотношение 0,352
Дата добавления: 2016-02-04 ; просмотров: 4136 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Построение гистограммы распределения погрешностей
Определение среднеквадратической погрешности результата измерения
Вычислить значение среднеквадратической погрешности результата измерения, т.е. погрешности σA, с которой определено среднеарифметическое значение Rср: 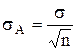

Указанное построение проводится для качественной проверки соответствия закона распределения погрешностей, полученных при многократных наблюдениях, нормальному закону распределения. Построение гистограммы провести в следующем порядке.

2 Заполнить таблицу статистического ряда (табл.1.2). Для этого по табл.1.1 подсчитать число Sj остаточных погрешностей, лежащих в интервале 0 – a, а – 2а, 2а – 3а отдельно с плюсом и минусом. Числа Sj записать в табл. 1.2. В ту же таблицу внести частоты появления погрешностей, определяемые для каждого интервала как отношение числа погрешностей Sj к общему числу погрешностей n. Погрешности, точно совпадающие по значению с границей интервала, могут быть отнесены либо к j–1 интервалу, либо к j интервалу. Например, если таких погрешностей две, то их целесообразно разделить между смежными интервалами. Для определения высот прямоугольников гистограммы (см. рис.1.3) нужно частоты появления погрешностей разделить на величину интервалов. Вычисленные значения Sj/na внести в табл.1.2.
| Интервалы | 0 – a | a – 2a | 2a – 3a | |||
| Знак погрешностей | + | – | + | – | + | – |
| Число остаточных погрешностей Sj | ||||||
| Частоты появления погрешностей Sj / n | ||||||
| Высоты прямоугольников гистограммы Sj / na | ||||||
Середины интервалов 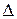 Ri Ri | ||||||
P( 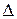 Ri) Ri) |
3 Построить гистограмму, для чего по оси абсцисс отложить численные значения интервалов ±a, ±2a, ±3a. На каждом интервале, как на основании построить прямоугольник, площадь которого равна частоте появления погрешностей, лежащих в данном интервале. Значения высот прямоугольников взять из табл.1.2. Площадь гистограммы равна единице (из построения).
4 Построить на том же графике теоретическую кривую нормального распределения в соответствии с уравнением (1.1). Значения P(DRi) определить для точки DRi = 0 и середин интервалов DRi = ±a/2; ±3a/2, ±5a/2. Полученные значения занести на построенную гистограмму. Соединить нанесенные точки плавной кривой. Сравнить гистограмму с теоретической кривой нормального распределения.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Обработка результатов многократных измерений



Диапазон измерительных величин и их количество постоянно растут, и поэтому возрастает и сложность измерений. Они перестают быть однократным действием и превращаются в сложную процедуру подготовки и проведения измерительного эксперимента и обработки полученной информации.
Другой причиной важности измерений является их значимость. Основа любой формы управления, анализа, прогнозирования, контроля или регулирования – достоверная исходная информация, которая может быть получена лишь путем измерения требуемых физических величин, параметров и показателей. Только высокая и гарантированная точность результатов измерений обеспечивает правильность принимаемых решений.
Поэтому в случае, когда случайная составляющая погрешности однократного измерения может превысить требуемые по условиям задачи значение, выполняют ряд последовательных отдельных измерений и получают одно многократное измерение, погрешность которого может быть уменьшена методами математической статистики.
Многократным называют измерение физической величины одного размера, результат которого получен из нескольких следующих друг за другом измерений, то есть состоящее из ряда однократных измерений.
Из опыта известно, что ни одно измерение, как бы тщательно оно не проводилось, не может дать абсолютно точный результат, вследствие чего часто говорят о наличии ошибок и погрешностей при проведении измерительного эксперимента. Всегда существует множество факторов, в том числе и случайных, приводящих к искажениям получаемой измерительной информации.
При условии исключения из результатов экспериментов систематических и грубых ошибок, остается лишь случайная составляющая погрешности. Случайную ошибку можно рассматривать как суммарный эффект действия многих факторов, каждый из которых не проявляет себя отчетливо. Поэтому случайные ошибки при многократных измерениях получаются различными как по величине, так и по знаку. Их невозможно учесть как систематические, но можно учесть их влияние на оценку истинного значения измеряемой величины. Анализ случайных ошибок является важнейшим разделом математической обработки экспериментальных данных.
Для получения результатов, минимально отличающихся от истинных значений величин, проводят многократные наблюдения за измеряемой величиной с последующей математической обработкой опытных данных. Поэтому наибольшее значение имеет изучение погрешности как функции номера наблюдения, т.е. времени ∆(t). Тогда отдельные значения погрешностей можно будет трактовать как набор значений этой функции:
В общем случае погрешность является случайной функцией времени, которая отличается от классических функций математического анализа тем, что нельзя сказать, какое значение она примет в момент времени t. Можно указать лишь вероятности появления ее значений в том или ином интервале.
При проведении измерений целью является оценка истинного значения измеряемой величины, которое до опыта неизвестно. Результат измерения включает в себя помимо истинного значения еще и случайную погрешность, следовательно, сам является случайной величиной. В этих условиях фактическое значение случайной погрешности, полученное при поверке, еще не характеризует точности измерений, поэтому не ясно, какое же значение принять за окончательный результат измерения и как охарактеризовать его точность.
Ответ на эти вопросы можно получить, используя при метрологической обработке результатов измерения методы математической статистики, имеющей дело именно со случайными величинами.
Рассмотрим результат наблюдений х за постоянной физической величиной Q как случайную величину, принимающую различные значения Z, в различных наблюдениях за ней. Значения Xi будем называть результатами отдельных наблюдений.
Наиболее универсальный способ описания случайных величин заключается в отыскании их интегральных или дифференциальных функций распределения.
Под интегральной функцией распределения результатов наблюдений понимается зависимость вероятности того, что результат наблюдения Xi в i–м опыте окажется меньшим некоторого текущего значения х, от самой величины х:
Здесь и в дальнейшем большие буквы используются для обозначения случайных величин, а маленькие – значений, принимаемых случайными величинами.
Более наглядным является описание свойств результатов наблюдений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей:
Свойства плотности распределения вероятности:
― 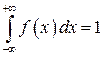
― 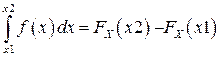
От дифференциальной функции распределения легко перейти к интегральной путем интегрирования:
Размерность плотности распределения вероятностей обратна размерности измеряемой величины, поскольку сама вероятность – величина безразмерная.
Таким образом, вероятность попадания результата наблюдения или случайной погрешности в заданный полуоткрытый интервал равна площади, ограниченной кривой распределения, осью абсцисс и перпендикулярами к ней на границах этого интервала. Необходимо отметить, что результаты наблюдений в значительной степени сконцентрированы вокруг истинного значения измеряемой величины и по мере приближения к нему элементы вероятности их появления возрастают. Это дает основание принять за оценку истинного значения измеряемой величины координату центра тяжести фигуры, образованной осью абсцисс и кривой распределения, и называемую математическим ожиданием результатов наблюдений:
Функция распределения является самым универсальным способом описания поведения случайных погрешностей. Однако для определения функций распределения необходимо проведение весьма кропотливых научных исследований и обширных вычислительных работ. Поэтому к такому способу описания случайных погрешностей прибегают иногда при исследовании принципиально новых мер и измерительных приборов.
Значительно чаще бывает достаточно охарактеризовать случайные погрешности с помощью ограниченного числа специальных величин, называемых моментами [3].
Начальным моментом n–го порядка результатов наблюдений называется интеграл вида
т.е. первый начальный момент совпадает с математическим ожиданием результатов измерений.
Центральным моментом n–го порядка результатов наблюдений называется интеграл вида
Вычислим первый центральный момент:
Таким образом, первый центральный момент результатов наблюдений равен нулю. Важно отметить, что начальные и центральные моменты случайных погрешностей совпадают между собой и с центральными моментами результатов наблюдений, поскольку математическое ожидание случайных погрешностей равно нулю.
Особое значение наряду с математическим ожиданием результатов наблюдений имеет второй центральный момент, называемый дисперсией результатов наблюдений.
Дисперсия D[X] случайной погрешности равна дисперсии результатов наблюдений и является характеристикой их рассеивания относительно математического ожидания.
Если математическое ожидание результатов наблюдений можно рассматривать в механической интерпретации как абсциссу центра тяжести фигуры, заключенной между кривой распределения и осью Ох, то дисперсия является аналогом момента инерции этой фигуры относительно вертикальной оси, проходящей через центр тяжести.
Дисперсия имеет размерность квадрата измеряемой величины, поэтому она не совсем удобна в качестве характеристики рассеивания. Значительно чаще в качестве последней используется положительное значение корня квадратного из дисперсии, называемое средним квадратическим отклонением результатов наблюдений:
С помощью среднеквадратического отклонения можно оценить вероятность того, что при однократном наблюдении случайная погрешность по абсолютной величине не превзойдет некоторой наперед заданной величины ε, т.е. вероятность P <|δ|>2 x результатов наблюдений, т. е.
Оценка дисперсии результатов наблюдений при малом n является немного смещенной, поэтому точечную оценку дисперсии принято определять как
а оценку среднеквадратического отклонения результатов наблюдений как
Дисперсия оценки Sx среднеквадратического отклонения составляет
С помощью полученных оценок итог измерений можно записать в виде
что уже позволяет сделать некоторые выводы относительно точности проведенных измерений.
В настоящее время большое распространение получила оценка с помощью интервалов. Смысл оценки параметров с помощью интервалов заключается в нахождении интервалов, называемых доверительными, между границами которых с определенными вероятностями (доверительными) находятся истинные значения оцениваемых параметров.
Вначале остановимся на определении доверительного интервала для среднего арифметического значения измеряемой величины. Предположим, что распределение результатов наблюдений нормально и известна дисперсия σ 2 x Найдем вероятность попадания результата наблюдений в интервал (mx – tpσx, mx + tpσx). Согласно формуле для интегральной функции нормированного нормального распределения Ф(tp)
и, если систематические погрешности исключены (mx=Q),
Это означает, что истинное значение Q измеряемой величины с доверительной вероятностью P=2Ф(tp)–1 находится между границами доверительного интервала (X – tpσx, X + tpσx).
Половина длины доверительного интервала tpσx называется доверительной границей случайного отклонения результатов наблюдений, соответствующей доверительной вероятности Р. Для определения доверительной границы (при выполнении перечисленных условий) задаются доверительной вероятностью, например Р=0,95 или Р=0,995 и по формулам
определяют соответствующее значение 2Ф(tp) интегральной функции нормированного нормального распределения. Затем по данным таблицы 1 приложения находят значение коэффициента tp и вычисляют доверительное отклонение tpσx Проведение многократных наблюдений позволяет значительно сократить доверительный интервал. Действительно, если результаты наблюдений Xi (i=l, 2. n) распределены нормально, то нормально распределены и величины Xi/n, а значит, и среднее арифметическое, являющееся их суммой. Поэтому имеет место равенство
где tp определяется по заданной доверительной вероятности Р.
Полученный доверительный интервал, построенный с помощью среднего арифметического результатов n независимых повторных наблюдений, в «корень из» n раз короче интервала, вычисленного по результату одного наблюдения, хотя доверительная вероятность для них одинакова. Это говорит о том, что сходимость измерений растет пропорционально корню квадратному из числа наблюдений.
Половина длины нового доверительного интервала
называется доверительной границей погрешности результата измерений, а итог измерений записывается в виде
Теперь рассмотрим случай, когда распределение результатов наблюдений нормально, но их дисперсия неизвестна. В этих условиях пользуются отношением
называемым дробью Стьюдента. Входящие в нее величины вычисляют на основании опытных данных; они представляют собой точечные оценки математического ожидания и среднеквадратического отклонения результатов наблюдений.
Плотность распределения этой дроби, впервые предсказанного Госсетом, писавшим под псевдонимом Стьюдент, выражается следующим уравнением:
где S(t,k) – плотность распределения Стьюдента. Величина k называется числом степеней свободы и равна n–1. Вероятность того, что дробь Стьюдента в результате выполненных наблюдений примет некоторое значение в интервале (‑tp, +tp), согласно выражению, вычисляется по формуле:
или, поскольку S(t,k) является четной функцией аргумента t,
Подставив вместо дроби Стьюдента t ее выражение через истинное значение результата, точечные оценки математического ожидания и среднеквадратического отклонения результатов наблюдений, получим окончательно
Величины tp, вычисленные по этим формулам, были табулированы Фишером для различных значений доверительной вероятности Р в пределах 0,10 – 0,99 при k=n–1=1,2,…,30. В таблице 5 приведены значения tp для наиболее часто употребляемых доверительных вероятностей Р.
Итог измерений записывается в виде
В тех случаях, когда распределение случайных погрешностей не является нормальным, все же часто пользуются распределением Стьюдента с приближением, степень которого остается неизвестной.
Кроме того, на основании центральной предельной теоремы теории вероятностей можно утверждать, что при достаточно большом числе наблюдений распределение среднего арифметического как суммы случайных величин Xi/n будет сколь угодно близким к нормальному.
Таблица 5– Коэффициент Стьюдента
| k | P | ||||
| 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | |
| 3,08 | 6,31 | 12,71 | 31,8 | 63,7 | |
| 1,89 | 2,92 | 4,30 | 6,96 | 9,92 | |
| 1,64 | 2,35 | 3,18 | 4,54 | 5,84 | |
| 1,53 | 2,13 | 2,77 | 3,75 | 4,60 | |
| 1,48 | 2,02 | 2,57 | 3,36 | 4,03 | |
| 1,44 | 1,94 | 2,45 | 3,14 | 4,71 | |
| 1,42 | 1,90 | 2,36 | 3,00 | 3,50 | |
| 1,40 | 1,86 | 2,31 | 2,90 | 3,36 | |
| 1,38 | 1,83 | 2,26 | 2,82 | 3,25 | |
| 1,37 | 1,81 | 2,23 | 2,76 | 3,17 | |
| l,363 | 1,80 | 2,20 | 2,72 | 3,11 | |
| 1,36 | 1,78 | 2,18 | 2,68 | 3,06 | |
| 1,35 | 1,77 | 2,16 | 2,65 | 3,01 | |
| 1,35 | 1,76 | 2,14 | 2,62 | 2,98 | |
| 1,34 | 1,75 | 2,13 | 2,60 | 2,95 | |
| 1,34 | 1,75 | 2,12 | 2,58 | 2,92 | |
| 1.33 | 1,74 | 2,11 | 2,57 | 2,90 | |
| 1,33 | 1,73 | 2,10 | 2,55 | 2,88 | |
| 1,33 | 1,73 | 2,09 | 2,54 | 2,86 | |
| 1,38 | 1,73 | 2,09 | 2,53 | 2,85 | |
| 1,32 | 1,72 | 2,08 | 2,52 | 2,83 | |
| 1,32 | 1,72 | 2,07 | 2,51 | 2,82 | |
| 1,32 | 1,71 | 2,07 | 2,50 | 2,81 | |
| 1,32 | 1,71 | 2,06 | 2,49 | 2,80 | |
| 1,32 | 1,71 | 2,06 | 2,49 | 2,79 | |
| 1,32 | 1,71 | 2,06 | 2,48 | 2,78 | |
| 1,31 | 1,70 | 2,05 | 2,47 | 2,77 | |
| 1,31 | 1,70 | 2,05 | 2,47 | 2,76 | |
| 1,31 | 1,69 | 2,05 | 2,46 | 2,76 | |
| 1,30 | 1,68 | 2,02 | 2,42 | 2,70 | |
| 1,30 | 1,67 | 2,00 | 2,39 | 2,66 | |
| 1,29 | 1,66 | 1,98 | 2,36 | 2,62 | |
| >120 | 1,28 | 1,65 | 1,96 | 2,33 | 2,58 |
Если эксперимент состоит в многократном измерении одной и той же величины постоянного размера, то результатом измерения является группа из n независимых показаний (измерений), составляющих массив экспериментальных данных. Главной особенностью измерительного эксперимента, проводимого с использованием статистической обработки полученных данных, является получение и использование большого объема апостериорной измерительной информации.
При статистической обработке многократных показаний решаются три основные задачи:
― оценивание области неопределенности исходных экспериментальных данных;
― нахождение более точного усредненного результата измерения;
― оценивание погрешности этого усредненного результата, то есть более узкой области неопределенности.
При практическом выполнении статистической обработки многократных показаний необходимо знание методов определения по экспериментальным данным числовых характеристик распределений случайной величины. Основной смысл усреднения многократных показаний заключается в том, что найденная усредненная оценка координаты их центра имеет меньшую случайную погрешность, чем отдельные показания, по которым она находится. При этом принципиальным является допущение, что показания подчиняются нормальному закону распределения вероятности. Справедливость этого допущения необходимо проверять.
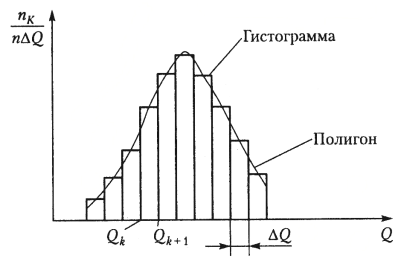 |
Правдоподобно или нет допущение о том, что полученные показания подчиняются нормальному закону распределения вероятности, можно предварительно оценить по виду гистограммы, построенной на основании полученных экспериментальных данных (рисунок 6).
Рисунок 6 – Гистограмма
Для отображения n полученных показаний СИ в виде гистограммы область численных значений между наименьшим и наибольшим показаниями L = Qmax ‑ Qmin делят на интервалы одинаковой ширины ΔQ и определяют число показаний nk, попавших в каждый из полученных интервалов. Полученные результаты изображают графически, откладывая по оси абсцисс полученные максимальное и минимальное показания с обозначением границ интервалов между ними, а по оси ординат – величину nk/(nΔQ). Построив над каждым из интервалов прямоугольники, основанием которых является ширина интервалов, а высотой – nk/(nΔQ), получим гистограмму, дающую представление о плотности распределения вероятности полученных показаний в данном эксперименте. Относительную частоту попаданий nk/n можно условно приравнять к вероятности попадания в конкретный интервал, а высоту прямоугольника считать равной эмпирической плотности вероятности рk = nk/(nΔQ). Тогда площадь каждого прямоугольника равна вероятности попадания в интервал, а площадь всех прямоугольников будет равна единице, что соответствует условию нормировки (k – число интервалов):
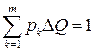
Полигон представляет собой ломаную кривую, соединяющую середины верхних оснований столбцов гистограммы. Полученная таким образом кусочнолинейная аппроксимация более наглядно, чем гистограмма, отражает форму искомой кривой распределения
При практической обработке результатов измерений можно последовательно выполнить следующие операции:
1. Записать результаты измерений;
2. Вычислить среднее значение из n измерений:
4. Вычислить квадраты погрешностей отдельных измерений Vi 2 ;
5. Если несколько измерений резко отличаются по своим значениям от остальных измерений, то следует проверить не являются ли они промахом. При исключении одного или нескольких измерений п.п.1. 4 повторить;
6. Определяется средняя квадратичная погрешность результата серии измерений:
7. Задается значение надежности a;
8. Определяется коэффициент Стьюдента ta(n) для выбранной надежности a и числа проведенных измерений n;
9. Находятся границы доверительного интервала: Dх = ta (n)Sa
10. Если величина погрешности результата измерений (п. 9) окажется сравнимой с величиной d погрешности прибора, то в качестве границы доверительного интервала следует взять величину:
11. Записать окончательный результат: X = a ± Dx;
12. Оценить относительную погрешность результата серии измерений:
13. Результат измерений записывается в виде