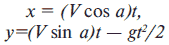Для чего строятся модели
Что такое модели и моделирование — 5 этапов моделирования, когда и какие модели применяются
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Что общего между девушкой на подиуме, игрушечной машинкой и изображением атома на экране монитора? Во всех случаях мы говорим о моделях.
Это понятие плотно вошло в повседневную речь, но немногие понимают его подлинное значение и умеют применять осознанно.
Без всякого занудства я расскажу о моделях и моделировании все, что нужно знать.
Что такое модель
Термин образовался от латинского слова modulus — «мера, аналог, образец».
Под «моделью» понимается образ некого объекта или явления, который отражает лишь отдельные свойства.
Например, глобус – это модель земного шара. Он статичен, а не вращается вокруг солнца. Не может похвастаться собственной силой притяжения. Не имеет атмосферы. На поверхности глобуса не живут крошечные человечки. Он воспроизводит внешний вид нашей планеты, не затрагивая другие характеристики.
Военачальник разрабатывает план сражения. Чтобы обозначить ландшафт, он создает модель поля боя на своем столе. Вот этот камень будет горой, коробок спичек – вражеским танком, а зеленый платок – лесом.
При моделировании важна степень соответствия модели и реального объекта.
Поставив камешек не туда, можно проиграть настоящую битву.
Но избыточная схожесть также вредит делу — усложняет процесс и отвлекает от сути.
Стратег слишком увлекся, потратил время на воспроизведение полной копии танка в миниатюре. Враг начал наступление, застал военачальника врасплох, пока тот собирал макет.
Американский словарь английского языка дает такое определение:
«Модель — это упрощенное описание сложного объекта или явления».
Земля имеет шарообразную форму, но для простоты говорят, что она круглая.
Моделирование — это.
Моделирование — это метод познания. Он заключается в исследовании предметов, систем, процессов и явлений на основе их моделей.
Вот мы возвели небоскреб в зоне с высокой сейсмической активностью. Теперь хотим выяснить, выдержит ли постройка толчки земной коры. Как это сделать? Проведем эксперимент: произведем подрыв, чтобы вызвать землетрясение. Если здание устоит — все хорошо.
Но вот проблема — затея дорогостоящая, может привести к человеческим жертвам, уничтожить сам предмет исследования. Гораздо проще создать модель небоскреба в компьютерной программе, задать силу виртуального землетрясения и проверить устойчивость, не вставая с дивана.
Что можно моделировать:
5 этапов моделирования
Процесс состоит из 5 этапов:
Исследователь выбирает те части, которые его интересуют, а остальные отбрасывает, чтобы не мешались. Один объект может иметь несколько моделей, каждая из которых отображает некоторые из его особенностей.
Например, мы хотим изучить человека:
Получаются 3 разных описания человека, которые только частично замещают оригинал.
Моделирование — это циклический процесс. Исследователь возвращается к самому началу, снова строит модель, но уже более точную.
С каждым кругом он получает все больше информации о предмете изучения.
Моделирование – это воссоздание и изучение фрагмента реальности для исследовательских целей.
Метод применяется, когда необходимо:
Когда применяется моделирование
Зачем экспериментировать с моделями, когда есть оригинал?
Существуют ситуации, когда без построения модели не обойтись:
Какие бывают модели (их виды)
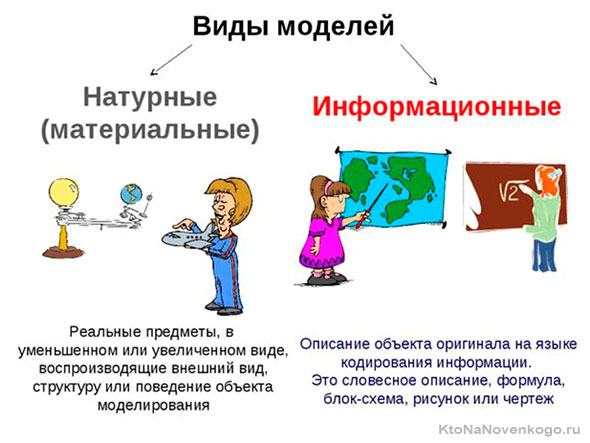
По своему характеру они делятся на 2 вида: материальные и информационные.
Материальные модели можно потрогать, увидеть, услышать, понюхать. Они воспроизводят физические особенности изучаемой системы, явления или процесса.
Деревянный макет здания – это изделие, которое отражает некоторые свойства реальной постройки. Плюшевый мишка – упрощенное представление большого медведя. Маленький ребенок приходит в зоопарк и легко узнает в грозном животном прообраз своей игрушки.
Информационные модели не существуют в реальном мире. Это набор информации, выраженный определенным образом – вербальным или знаковым.
Примерами знакового обозначения могут быть математические формулы, схемы, графики и рисунки. Вербальное представление – это слова или мысли. Например, модель поведения при переходе регулируемого перекрестка: посмотреть на светофор, если горит зеленый человечек, нужно убедиться, что нет машин. Только потом можно идти.
Более подробно на эту тему смотрите в видео:
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (2)
Компьютерное моделирование вряд ли сможет заменить полноценный эксперимент с физической моделью, тем более, что программу пишут люди, а они могут ошибаться. На модели же можно проверить, к примеру, аэродинамические качества объекта, поместив уменьшенную копию в аэродинамическую трубу, чего нельзя сделать с реальным объектом, например, пассажирским самолётом. Потому модели будут существовать всегда.
Раньше и дети моделированием увлекались, самолеты небольшие конструировали, а сейчас только в компьютерные стрелялки играют.
Цели моделирования



Рассмотрим теперь вопрос, для чего вообще нужно моделирование, в каких случаях можно обойтись без модели, исследуя собственно саму систему?
Моделирование имеет две основных цели:
— Прогнозирование, когда необходимо предсказать новые свойства или новые результаты (параметры) исследуемых систем, когда необходимо спрогнозировать развитие процесса.
Например, предприятие занимается составлением перспективного плана своего развития. Естественно, что для решения этой задачи необходимо проанализировать динамику развития рынка и спроса на продукцию предприятия. Но прогноз просто так, «глядя в потолок» не построишь. Единственный путь – построить математическую модель динамики спроса. В экономике моделирование применяется повсеместно. Если модель адекватна, то можно получить достаточно обоснованные перспективы развития предприятия. Во всяком случае, это будет хорошей поддержкой для принятия управленческих решений. Такие модели строятся и на уровне экономики Государства, отрасли, на уровне предприятии и на уровне решения локальных управленческих задач.
Но существуют процессы, которые смоделировать не только сложно, но и практически не возможно. Например, спрогнозировать динамику фондового рынка или курса доллара не получается – слишком много случайных факторов влияют на процесс. Модель получается не адекватная.
Например,предприятие выпускает большой ассортимент продукции, себестоимость выпуска которой различна и прибыль от реализации различных товаров так же различна. Требуется так построить производственный план, что бы прибыль была максимальной.
У человека всегда имеется две возможностидля достижения этих целей: провести исследования, экспериментируя непосредственно с реальной системой (натурные эксперименты), либо построить модель.
В каких случаях строятся модели? Модели строят только тогда, когда без них обойтись нельзя, поскольку моделирование – трудоемкая и дорогостоящая процедура. В случаях же, когда можно проводить прямое исследование систем, обходятся без моделей.
Бывают ситуации, когда модель построить нельзя, мы просто не имеем информации о реальном объекте. Такая ситуация называется «черный ящик». Здесь исследование будет заключаться в непосредственном воздействии на объект (в эксперименте) и фиксации реакций объекта.
Модели создаются, когда необходимо определить свойства и характеристики проектируемых объектов еще до их изготовления и при необходимости скорректировать, уточнить их структуру и параметры. Это позволяет получить проект работоспособной системы, которую не придется существенно дорабатывать тогда, когда она будет изготовлена. Таким образом, моделирование сокращает и удешевляет процесс проектирования и реализации систем.
Модели создаются, когда необходимо проверить поведение объектов в экстремальных условиях и режимах, с тем, чтобы знать, как они себя поведут и к каким последствиям это приведет. Очевидно, что такие эксперименты на реальном объекте могут быть не только дороги, но и небезопасны, в то время как моделирование позволяет получить нужную информацию о процессе или системе без лишних затрат и, главное, без негативных последствий.
Модель строится там, где непосредственное экспериментальное исследование может быть вообще неосуществимо. В ряде же случаев мы вообще не имеем возможности наблюдать систему в интересующем нас состоянии. Например, разбор аварии на техническом объекте приходится вести по ее протокольному описанию. Или, например, прогноз поведения космического корабля на орбите. Имеется в виду этап первоначальных исследований, до первого запуска космических аппаратов.
Таким образом, моделирование позволяет исследовать такие системы, прямой эксперимент с которыми:
Формальная схема моделирования
Рассмотрим саму схему моделирования, как происходит замещение объекта моделью.
Пусть мы имеем некоторую систему (объект – оригинал) А. Мы собираемся исследовать ее свойства S с помощью модели (например, математической модели).
Моделирование предполагает наличие некоторых знаний о системе.
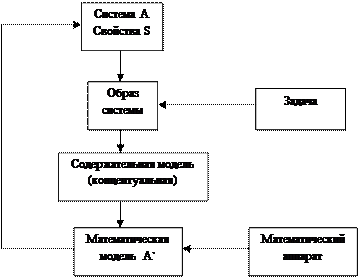
Рис.1. Общая схема моделирования.
Если исходная информация отсутствует, то и модель построить невозможно. В этом случае мы имеем ситуацию типа «черный ящик». Образ системы не сформирован. Исследование объекта производится методом проб.
Прежде чем строить саму математическую модель, мы описываем исследуемую систему и ее предполагаемые свойства на содержательном уровне.
Содержательное описание системы уже само является моделью. Такая содержательная модель называется концептуальной. Она содержит описание структуры, предполагаемых свойств, связей и известные значения параметров. Здесь формулируются гипотезы о поведении системы и все ограничения применимости будущей математической модели. Построение концептуальной модели является первым этапом моделирования.
Далее выбираем математический аппарат и создаем систему уравнений или арифметических соотношений. Таким образом мы создаем некоторый искусственный (математический) объект А, исследование которого средствами математики и должно ответить на поставленные вопросы о свойствах S системы. Мы переводим концептуальную модель на формальный математический язык.
В такой постановке А называется математической моделью системы А относительно совокупности S ее свойств.
В действительности мы моделируем не реальную систему А, а ее образ, сформированный нашим сознанием.
Результаты моделирования сравниваются со свойствами системы. Мы уточняем образ и соответственно модель.
Формальная схема моделирования включает ряд последовательных этапов:
— выбор нужного инструментария (математического аппарата) для модели;
— если модель реализуется программно, то существует этап разработки алгоритма и собственно программирования;
— интерпретация результатов моделирования;
— оценка валидности модели (валидность – достоверность результатов, способность выполнять задачу).
МНОГООБРАЗИЕ МОДЕЛЕЙ СИСТЕМ
Общая классификация
Прежде, чем приступать к моделированию, необходимо определиться какую модель мы собираемся создавать. Существуют различные виды моделей и различные признаки их классификации.
Чаще встречается классификация моделей по способам реализации (исполнения), это наиболее полная классификация, хотя четкой границы между классами провести всегда сложно.
По этому признаку все множество моделей можно разделить на три основных класса: физические, виртуальные и абстрактные.
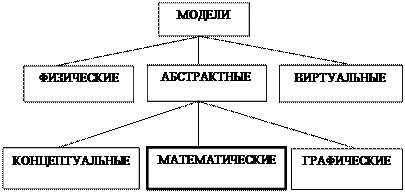 |
Рис.2. Общая классификация моделей (по форме представления)
Физические модели (они часто называются предметными).
Физические модели — это материальные модели, эквивалентные или подобные в той или иной степени оригиналу. В общем случае у физических моделей процесс функционирования такой же, как у оригинала. Он имеет ту же, или подобную физическую природу. Они различаются по критерию подобия. Критерием подобия является безразмерная величина, представляющая отношение одноименных физических величин объекта и модели.
Иногда физические модели выполняют в натуральную величину, например, при создании макетов космических модулей. Тогда критерий подобия равен единице.
Теория обеспечивала возможность достоверного переноса данных, полученных на модели, на «натуру», на свойства и параметры реального, но еще не существующего объекта.
Виртуальные модели.
Виртуальные модели – это в основном компьютерные визуальные модели реального или придуманного пространства (виртуальный – это кажущийся). Из определения понятно, что моделируются свойства некоторого пространства с эффектом присутствия в этом пространстве самого пользователя.
Интернет так же является моделью виртуального пространства. В этом пространстве реализуется вполне реально мировая интернет-экономика.
К виртуальным моделям относятся различные тренажеры. Например, тренажеры летного состава. Моделирование различных ситуаций на таком тренажере настолько реальны, что по физической и психологической нагрузке на человека такие модели практически не отличаются от реальных процессов.
В настоящее время виртуальные модели находят широкое использование в учебной практике. Как известно, процесс обучения может осуществляться в форме усвоения обучаемым «готового» знания и в форме учебного исследования. Источник готового знания – это книга. Учебное исследование – это эксперимент. Виртуальная обучающая модель (манипулятивная динамическая модель) как раз и дает возможность проведения экспериментов с объектами виртуальной учебной среды. Это метод компьютерного воссоздания формы, структуры, функций какой либо живой системы, либо неживой природы. Обучающийся в интерактивном режиме может изменять параметры системы, исследуя ее реакцию изучать саму систему с различных сторон ее проявления. Это новая информационная культура обучения.
Абстрактные модели.
Абстрактные модели часто называются информационными. Они отражают информационную сторону системы с помощью языковых, математических, графических, алгоритмических и других средств абстрагирования. Они не имеют физического сходства с оригиналом и не обладают его физическими свойствами. В абстрактных моделях физические свойства системы представлены их формализованными, абстрактными, символическими отображениями.
Следует отметить, что границы между классами моделей провести, достаточно четко не удается. Поэтому классификация не всегда бывает однозначной. Например, виртуальные компьютерные модели, используемые в процессе преподавания школьникам естественных наук. С одной стороны, действительно, это виртуальные модели. Они организуют деятельность учащихся в виртуальной среде, максимально приближенной средствами компьютерной графики к процессу реализации реальных экспериментов. С другой стороны, эти модели вполне законно можно отнести к классу абстрактных моделей. Они фактически являются компьютерной реализацией дифференциальных уравнений, моделирующих реальные физические процессы.
Абстрактные модели можно разделить на концептуальные, графические и математические.
Концептуальными моделями являются языковые (вербальные) описания систем (описание свойств и параметров на некотором естественном языке, текстовые материалы проектной документации, словесное описание результатов технического эксперимента).
Графическая модель – это представление систем средствами графики.
К графическим моделям относятся графы, графики, логические схемы и т.д. Блок-схемы алгоритмов программ так же являются графическими моделями.
Сюда же можно отнести конструкторские чертежи, графические изображения объектов. Хотя геометрия и является одной из отраслей математики, целесообразно к этому классу отнести и геометрические модели объектов.
Математические модели представляют собой формализованное описание изучаемой системы с помощью абстрактного языка, в частности, с помощью формул, уравнений, неравенств, логических условий, матриц, операторов и т. д., отображающих процесс функционирования системы.
Для чего строятся модели
Моделирование и формализация
9.1. Понятие о моделях
Каждый объект имеет большое количество различных свойств. В процессе построения модели выделяются главные, наиболее существенные из них. Так, модель самолета должна иметь геометрическое подобие оригиналу, модель атома – правильно отражать физические взаимодействия, архитектурный макет города – ландшафт и т. д.
Модель – это некий новый объект, который отражает существенные особенности изучаемого объекта, явления или процесса.
В разных науках объекты и процессы исследуются под разными углами зрения и строятся различные типы моделей. В физике изучаются процессы взаимодействия и движения объектов в химии – их внутреннее строение, в биологии – поведение живых организмов и т. д.
Возьмем в качестве примера человека; в разных науках он исследуется в рамках различных моделей. В механике его можно рассматривать как материальную точку, в химии – как объект, состоящий из различных химических веществ, в биологии – как систему, стремящуюся к самосохранению, и т. д.
С другой стороны, разные объекты могут описываться одной моделью. Так, в механике различные материальные тела (от планеты до песчинки) часто рассматриваются как материальные точки.
Один и тот же объект иногда имеет множество моделей, а разные объекты описываются одной моделью.
Модель нужна нам тогда, когда мы хотим что-то описать или представить. Например, конструкторы при разработке новых самолетных двигателей должны проверить, как он поведет себя в сложных полетных условиях. Осуществлять проверку в реальных условиях – значит подвергать опасности жизнь летчика-испытателя, да и это не всегда возможно. Но можно смоделировать все возможные полетные условия на специальных испытательных стендах. Это и безопасней, да и диапазон условий может быть значительно шире. А если использовать компьютерное моделирование, основанное на знании физических законов и математических закономерностей работы двигателя, можно значительно сократить программу стендовых испытаний и получить реальную экономию времени, средств, материалов. Чтобы объяснить, почему для европейцев январь – зимний месяц, а для австралийцев – летний, не обойтись без показа глобуса или рисунка, объясняющих, каким образом Земля вращается вокруг своей оси и вокруг Солнца.
Любая модель каким-то образом соответствует объекту, подобна ему. Причем соответствие может быть:
1) по внешнему виду (похожесть);
2) по структуре (выделены составляющие элементы объекта и указаны их взаимосвязи);
3) по поведению (модель реагирует на внешнее воздействие таким же образом, как это делает объект, либо находится в подобных отношениях с другими объектами).
Любая модель строится в соответствии с некоторой целью, которая заранее определяется тем, кто занимается моделированием, т. е. субъектом моделирования.
Модель является либо представлением (реальным, воображаемым или изобразительным), либо описанием некоторых свойств объекта. Те или иные свойства выбираются в зависимости от того, зачем, с какой целью строится модель, для чего она предназначена. Такие свойства называются существенными для данной модели с точки зрения цели моделирования. Существенность и несущественность определенных свойств и признаков – понятия относительные, они зависят от решаемой задачи.
Модель создается для получения информации об объекте, необходимой для решения поставленной задачи. Никакая модель не может заменить сам объект. Но при решении конкретной задачи, когда нас интересуют определенные свойства изучаемого объекта, модель оказывается полезным, а подчас и единственным инструментом исследования.
• построение моделей реально существующих объектов (предметов, явлений, процессов);
• замена реального объекта его подходящей копией – имитация;
• исследование объектов познания на их моделях.
Моделирование является неотъемлемым элементом любой целенаправленной деятельности.
Моделирование – метод познания, состоящий в создании и исследовании моделей.
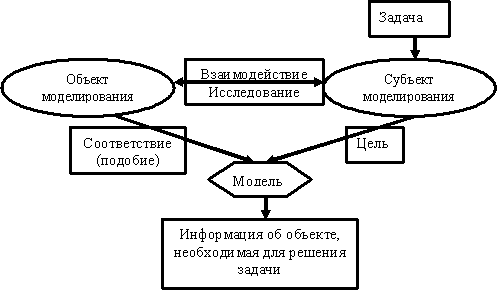
Общую схему моделирования можно представить следующим образом:
Рисунок 9.1. Общая схема моделирования
Решение любой практической задачи всегда связано с исследованием, преобразованием некоторого объекта (материального или информационного) или управления им.
Цель моделирования возникает, когда субъект моделирования решает стоящую перед ним задачу, и зависит как от решаемой задачи, так и от субъекта моделирования. То есть цель моделирования имеет двойственную природу: с одной стороны, она объективна, так как вытекает из задачи исследования, а с другой – субъективна, поскольку зависит от субъекта моделирования (его опыта интересов, мотивов деятельности и т. д.).
• Для одного объекта один субъект может построить несколько моделей, если он решает разные задачи, приводящие к разным целям моделирования.
• Для одного объекта разные субъекты могут построить разные модели, даже если задача моделирования у них одна.
• Разные объекты могут иметь одинаковые по виду модели, даже если их строили разные субъекты исходя из разных целей моделирования.
Все многообразие моделей делится на три класса.
1. Материальные (натурные) модели:
– некие реальные предметы (макеты, муляжи, эталоны);
– уменьшенные или увеличенные копии, воспроизводящие внешний вид моделируемого объекта, его структуру (глобус, модель кристаллической решетки) или поведение (радиоуправляемая модель самолета, велотренажер).
2. Абстрактные модели (геометрическая точка, математический маятник, идеальный газ, бесконечность).
3. Информационные модели – описание моделируемого объекта на одном из языков кодирования информации (словесное описание схемы, чертежи, карты, рисунки, научные формулы, программы и т. д.). Информационная модель, как и любой другой вид информации, должна иметь свой материальный носитель. Им может быть бумага, классная доска, пластинка, дискета и т. д. На этом носителе модель может быть записана различными способами: с помощью чернил, мела или типографского оттиска; световое изображение, полученное с помощью проекционной аппаратуры, изображение на экране монитора, и т. д.
Процесс создания модели проходит следующие этапы:
1. Постановка цели моделирования.
2. Анализ всех известных субъекту моделирования свойств объекта.
3. Анализ выделенных свойств и выделение существенных свойств и признаков с точки зрения целей моделирования. Для одного и того же объекта при разных целях моделирования существенными будут считаться разные свойства. Нет единого верного для всех случаев способа (правила, алгоритма) выделения существенных признаков, свойств, отношений. Иногда они очевидны, а иногда приходится построить много разных моделей с различными наборами этих свойств, прежде чем будет достигнута цель моделирования. От того, насколько правильно и полно выделены существенные признаки, зависит соответствие построенной модели заданной цели, т. е. ее адекватность цели моделирования.
4. Выбор формы представления модели. Адекватность модели объекту моделирования зависит от того, в какой форме отображаются выделенные нами существенные признаки. Формами представления моделей могут быть: словесное описание, чертеж, таблица, схема, алгоритм, компьютерная Программа и т. д. Пример: объект моделирования – дачный участок (цель моделирования – определить площадь участка; существенные признаки – форма участка, его размеры, форма представления модели – формула площади прямоугольника, модель – S = а* b).
5. Формализация – это процесс построения информационных моделей с помощью формальных языков. Результатом этапа формализации является информационная модель.
6. Анализ полученной модели на непротиворечивость. Если построенная модель противоречива, то после выявления всех замеченных противоречий их необходимо устранить: исправить чертеж, изменить программу, уточнить формулу и т. д.
7. Анализ адекватности полученной модели объекту и цели моделирования.
9.2. Виды моделирования
Применительно к естественным и техническим наукам принято различать следующие виды моделирования:
• концептуальное моделирование, при котором совокупность уже известных фактов или представлений относительно исследуемого объекта или системы истолковывается с помощью некоторых специальных знаков, символов, операций над ними или с помощью естественного или искусственного языков;
• физическое моделирование, при котором модель и моделируемый объект представляют собой реальные объекты или процессы единой или различной физической природы, причем между процессами в объекте-оригинале и в модели выполняются некоторые соотношения подобия, вытекающие из схожести физических явлений;
• структурно-функциональное моделирование, при котором моделями являются схемы (блок-схемы), графики, чертежи, диаграммы, таблицы, рисунки, дополненные специальными правилами их объединения и преобразования;
• математическое (логико-математическое) моделирование, при котором моделирование, включая построение модели, осуществляется средствами математики и логики;
• имитационное (программное) моделирование, при котором логико-математическая модель исследуемого объекта представляет собой алгоритм функционирования объекта, реализованный в виде программного комплекса для компьютера.
Разумеется, перечисленные выше виды моделирования не являются взаимоисключающими и могут применяться при исследовании сложных объектов либо одновременно, либо в некоторой комбинации. Кроме того, в некотором смысле концептуальное и, скажем, структурно-функциональное моделирование неразличимы между собой, так как те же блок-схемы, конечно же, являются специальными знаками с установленными операциями над ними.
9.3. Информационное моделирование
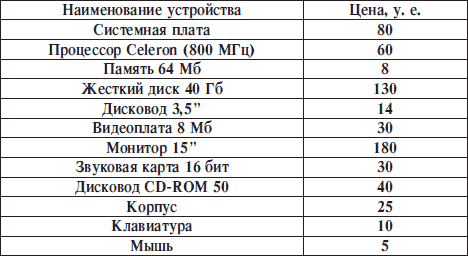
Табличные модели. Одним из наиболее часто используемых типов информационных моделей является таблица, которая состоит из строк и столбцов.
Построим, например, табличную информационную модель, отражающую стоимость отдельных устройств компьютера. Пусть в первом столбце таблицы содержится перечень объектов (устройств), входящих в состав компьютера, а во втором – их цена.
Рисунок 9.2. Информационная табличная модель
С помощью таблиц создаются информационные модели в различных предметных областях. Широко известно табличное представление математических функций, статистических данных, расписаний поездов и самолетов, уроков и т. д.
Табличные информационные модели проще всего формировать и исследовать на компьютере посредством электронных таблиц и систем управления базами данных.
Нас окружает множество различных объектов, каждый из которых обладает определенными свойствами. Однако некоторые группы объектов имеют одинаковые общие свойства, которые отличают их от объектов других групп.
Группа объектов, обладающих одинаковыми общими свойствами, называется классом объектов. Внутри класса могут быть выделены подклассы, объекты которых обладают некоторыми особенными свойствами, в свою очередь, подклассы можно делить на еще более мелкие группы и т. д. Такой процесс называется процессом классификации.
При классификации объектов часто применяются информационные модели, которые имеют иерархическую (древовидную) структуру. В иерархической информационной модели объекты распределены по уровням, причем элементы нижнего уровня – входят в состав одного из элементов более высокого уровня. Например, весь животный мир рассматривается как иерархическая система (тип, класс, отряд, семейство, род, вид), для информатики характерна иерархическая файловая система и т. д.
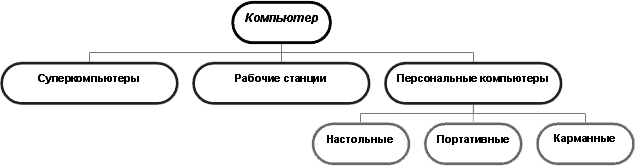
Рисунок 9.3. Информационная иерархическая модель
На рисунке 9.3 изображена информационная модель, которая позволяет классифицировать современные компьютеры. Полученная информационная структура напоминает дерево, которое растет сверху вниз (именно поэтому такие информационные модели называют иногда древовидными). В структуре четко просматриваются три уровня: от первого, верхнего, имеющего один элемент Компьютеры, мы спускаемся до третьего, нижнего, имеющего три элемента Настольные, Портативные, Карманные.
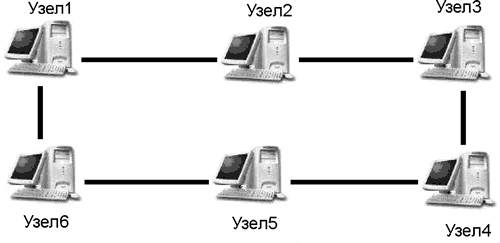
Сетевые информационные модели
Сетевые информационные модели применяются для отражения систем со сложной структурой, в которых связь между элементами имеет произвольный характер.
Рисунок 9.4. Сетевая информационная модель
Естественные языки служат для создания описательных информационных моделей. В истории науки известны многочисленные описательные информационные модели. Например, гелиоцентрическая модель мира, которую предложил Коперник, формулировалась следующим образом:
Земля вращается вокруг своей оси и вокруг Солнца; орбиты всех планет проходят вокруг Солнца.
С помощью формальных языков строятся формальные информационные модели (математические, логические и др.). Процесс построения информационных моделей с помощью формальных языков называется формализацией.
Одним из наиболее широко распространенных формальных языков является математический. Модели, сформированные с использованием математических понятий и формул, называются математическими моделями. Язык математики представляет собой совокупность формальных языков; о некоторых из них (алгебраическом, геометрическом) вы узнали в школе, с другими сможете познакомиться при дальнейшем обучении.
Язык алгебры позволяет формализовать функциональные зависимости между величинами. Так, Ньютон формализовал гелиоцентрическую систему мира Коперника, открыв законы механики и закон всемирного тяготения и записав их в виде алгебраических функциональных зависимостей. В школьном курсе физики рассматривается много разнообразных функциональных зависимостей, выраженных на языке алгебры, которые представляют собой математические модели изучаемых явлений или процессов.
Язык алгебры логики (алгебры высказываний) дает возможность строить формальные логические модели. С помощью алгебры высказываний формализуются (записываются в виде логических выражений) простые и сложные высказывания, выраженные на естественном языке. Путем построения логических моделей удается решать логические задачи, создавать логические модели устройств компьютера (сумматора, триггера) и т. д.
В процессе познания окружающего мира человечество постоянно прибегает к моделированию и формализации.
Формализация – это сведение некоторого содержания (содержания текста, смысла научной теории, воспринимаемых сигналов и пр.) к выбранной форме.
Например, оглавление книги – это формализация ее содержательных частей, а сам текст можно рассматривать как формализацию посредством языковых конструкций мыслей, идей, размышлений автора.
Возможность формализации опирается на фундаментальное положение, которое называют основным тезисом формализации: существует принципиальная возможность разделения объекта и его обозначения.
Суть объекта не меняется от того, как мы его назовем. Это значит, что мы можем назвать его так, чтобы это имя наилучшим образом соответствовало (с нашей точки зрения) данному объекту. Отрицание основного тезиса формализации означает, что имя объекта выражает его суть. В этом случае каждому объекту должно быть поставлено в соответствие только одно имя.
Из основного тезиса формализации следует сама идея моделирования.
Для обозначения объекта вводится некоторый набор знаков.
Знак – это элемент конечного множества отличных друг от друга элементов.
Основные черты знака:
1. Способность выступать в качестве заместителя объекта;
2. Неотождественность знака и объекта – знак никогда не может полностью заменить обозначаемое;
3. Многозначность соответствия «знак – объект».
9.5. Компьютерное моделирование
Язык – это знаковая система, используемая для целей коммуникации и познания.
Языки можно разделить на естественные и искусственные. Естественные (обычные, разговорные) языки складываются стихийно и в течение долгого времени. Искусственные языки создаются людьми для специальных целей или для определенных групп людей (язык математики, морской язык, языки программирования и т. д.). Характерной их особенностью является однозначная определенность их словаря, правил образования выражений и конструкций (строго формализованы). В естественных языках они – частично формализованы.
Каждый язык характеризуется:
• набором используемых знаков;
• правилом образования из этих знаков языковых конструкций;
• набором синтаксических, семантических и прагматических правил использования языковых конструкций.
Алфавит – это упорядоченный набор знаков, используемых в языке.
В информатике нас прежде всего интересуют модели, которые можно создавать и исследовать с помощью компьютера. С помощью компьютера можно создавать и исследовать множество объектов: тексты, графики, таблицы, диаграммы и пр. Компьютерные технологии накладывают все больший отпечаток на процесс моделирования, поэтому компьютерное моделирование можно рассматривать как особый вид информационного моделирования.
В последние годы благодаря развитию графического интерфейса и графических пакетов, широкое развитие получило компьютерное, структурно-функциональное моделирование. Суть имитационного компьютерного моделирования заключена в получении количественных и качественных результатов функционирования моделируемой системы по имеющейся модели. Качественные выводы, получаемые по результатам анализа модели, позволяют обнаружить неизвестные ранее свойства сложной системы: ее структуру, динамику развития, устойчивость, целостность и пр. Количественные выводы в основном носят характер прогноза некоторых будущих или объяснение прошлых значений параметров, характеризующих систему.
Предметом компьютерного моделирования могут быть: экономическая деятельность фирмы или банка, промышленное предприятие, информационно-вычислительная сеть, технологический процесс, процесс инфляции и т. д.
Цели компьютерного моделирования могут быть различными, но чаще всего это получение данных, которые могут быть использованы для подготовки и принятия решений экономического, социального, организационного или технического характера. Положено начало использованию компьютера даже при концептуальном моделировании, где он используется, например, при построении систем искусственного интеллекта.
Таким образом, мы видим, что понятие «компьютерное моделирование» значительно шире традиционного понятия «моделирование на ЭВМ» и нуждается в уточнении, учитывающем сегодняшние реалии.
Начнем с термина «компьютерная модель».
В настоящее время под компьютерной моделью чаще всего понимают:
• условный образ объекта или некоторой системы объектов (или процессов), описанный с помощью взаимосвязанных компьютерных таблиц, блок-схем, диаграмм, графиков, рисунков, анимационных фрагментов, гипертекстов и т. д. и отображающий структуру и взаимосвязи между элементами объекта. Компьютерные модели такого вида мы будем называть структурно-функциональными;
• отдельную программу, совокупность программ, программный комплекс, позволяющий с помощью последовательности вычислений и графического отображения их результатов воспроизводить (имитировать) процессы функционирования объекта, системы объектов при условии воздействия на объект различных (как правило, случайных) факторов. Такие модели мы будем далее называть имитационными моделями.
Компьютерное моделирование – метод решения задачи анализа или синтеза сложной системы на основе использования ее компьютерной модели.
Суть компьютерного моделирования заключена в получении количественных и качественных результатов по имеющейся модели. Качественные выводы, получаемые по результатам анализа, позволяют обнаружить неизвестные ранее свойства сложной системы: ее структуру, динамику развития, устойчивость, целостность и др. Количественные выводы в основном носят характер прогноза некоторых будущих или объяснения прошлых значений переменных, характеризирующих систему. Компьютерное моделирование для рождения новой информации использует любую информацию, которую можно актуализировать с помощью ЭВМ.
Основные функции компьютера при моделировании:
• выполнять роль вспомогательного средства для решения задач, решаемых обычными вычислительными средствами, алгоритмами, технологиями;
• выполнять роль средства постановки и решения новых задач, не решаемых традиционными средствами, алгоритмами, технологиями;
• выполнять роль средства конструирования компьютерных обучающе-моделирующих сред;
• выполнять роль средства моделирования для получения новых знаний;
• выполнять роль «обучения» новых моделей (самообучающиеся модели).
Разновидностью компьютерного моделирования является вычислительный эксперимент. Компьютерное моделированиев частности, вычислительный эксперимент становится новым инструментом, методом научного познания, новой технологией также из-за возрастающей необходимости перехода от исследования линейных математических моделей систем.
Предметом компьютерного моделирования могут быть: экономическая деятельность фирмы или банка, промышленное предприятие, информационно-вычислительная сеть, технологический процесс, любой реальный объект или процесс, например, процесс инфляции, и вообще любая Сложная Система. Цели компьютерного моделирования могут быть различными, однако наиболее часто моделирование является, как уже отмечалось ранее, центральной процедурой системного анализа, причем под системным анализом мы далее понимаем совокупность методологических средств, используемых для подготовки и принятия решений экономического, организационного, социального или технического характера.
Компьютерная модель сложной системы должна по возможности отображать все основные факторы и взаимосвязи, характеризующие реальные ситуации, критерии и ограничения. Модель должна быть достаточно универсальной, чтобы по возможности описывать близкие по назначению объекты, и в то же время достаточно простой, чтобы позволить выполнить необходимые исследования с разумными затратами.
Все это говорит о том, что моделирование, рассматриваемое в целом, представляет собой скорее искусство, чем сформировавшуюся науку с самостоятельным набором средств отображения явлений и процессов реального мира.
Процесс исследования поведения какого-либо объекта или системы объектов на компьютере можно разбить на следующие этапы:
• построение содержательной модели;
• построение математической модели;
• построение информационной модели и алгоритма;
• кодирование алгоритма на языке программирования;
Этапы и цели компьютерного моделирования
Рассмотрим процесс компьютерного математического моделирования, включающий численный эксперимент с моделью.
Моделирование занимает центральное место в исследовании объекта, процесса, явления. Оно позволяет обоснованно принимать решение: как совершенствовать объекты (процессы), надо ли создавать новые, как изменять процессы управления и, в конечном итоге, как менять окружающий мир в лучшую сторону.
Прежде чем браться за какую-либо работу, нужно четко представить себе отправной и конечный пункты деятельности, а также примерные ее этапы. То же можно сказать о моделировании.
Отправной пункт здесь – прототип. Им может быть существующий или проектируемый объект либо процесс.
Конечный этап – принятие решения. На этом этапе мы либо создаем новый объект (процесс), модель которого мы исследовали, либо улучшаем существующий, либо получаем о нем дополнительную информацию.
Рассмотрим процесс решения задачи на компьютере на следующем примере: изучим полет ядра, вытолкнутого легкоатлетом. Построим содержательную модель, в которой рассмотрим движение ядра в поле тяготения Земли. В этой модели рассматриваются только те параметры, которые характеризуют движение ядра (скорость и координаты), и отвлекаемся от других параметров (температура ядра, его цвет и т. д.).
Теперь построим математическую модель, которая основана на некоторых упрощениях, и это делает этап построения математической модели весьма ответственным, ведь неправильно выбранная модель приведет к неверным результатам.
Существующая физическая система описывается с помощью упрощенной математической модели. Ядро является материальной точкой, сопротивлением воздуха, скоростью ветра и параметрами спортсмена пренебрегаем, ускорение свободного падения считаем постоянным g= 9,8 м/с2. Ядро выталкивается спортсменом со скоростью V под углом к горизонту.
Математическая модель описывает объект моделирования с помощью уравнений.
Получим формулы зависимости координат снаряда от времени, учитывая, что по оси X движение равномерное, а по оси Y – равноускоренное:
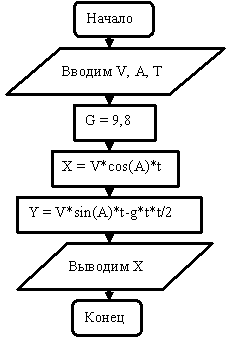
Теперь построим информационную модель и алгоритм. На этом этапе необходимо определить, какие величины являются аргументами, а какие – результатами алгоритма, а также определить тип этих величин. В нашем случае аргументами являются: угол вылета снаряда а, его начальная скорость V и время полета t. Результатом являются координаты X и Y. Все они являются переменными вещественного типа. Построим алгоритм, который позволяет определять значения результатов при различных значениях аргументов. Построенный алгоритм записываем в виде блок-схемы:
Рисунок 9.5. Блок-схема алгоритма расчета координат полета снаряда
Теперь можно проводить компьютерный эксперимент. Для этого необходимо загрузить программу в оперативную память компьютера и запустить на выполнение. Компьютерный эксперимент обязательно включает в себя анализ полученных результатов, на основании которого могут корректироваться все этапы решения задачи (математическая модель, алгоритм, программа).
1. Что такое модель?
2. Для чего используются модели?
3. Что такое моделирование?
4. Как классифицируются модели?
5. Какие этапы проходит процесс создания модели?
6. Какие виды моделирования различают?
7. Какие модели характеризуют информационное моделирование?
8. Что такое формализация?
9. Какими чертами должен обладать знак?
10. В чем заключается цель компьютерного моделирования?
11. Что понимается под компьютерной моделью?
12. Каковы основные функции и этапы компьютерного моделирования?