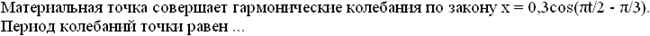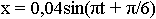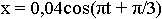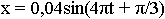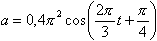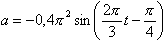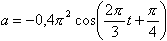Для плоской бегущей волны справедливо утверждение что
Ответ: 2. Ф4.3.2-3 Для плоской волны справедливо утверждение 1: Амплитуда волны не зависит от расстояния до источника колебаний (при условии
| Для плоской волны справедливо утверждение… | 1: Амплитуда волны не зависит от расстояния до источника колебаний (при условии, что поглощением среды можно пренебречь).* 2: Волновые поверхности имеют вид концентрических сфер. 3: Амплитуда волны обратно пропорциональна расстоянию до источника колебаний (в непоглощающей среде). |
1) Амплитуда волны не зависит от расстояния до источника колебательных движений – это характеристика плоской волны.
2) Волновые поверхности имеют вид концентрических сфер – это также характерно для сферических волн.
3) Амплитуда волны обратно пропорциональна расстоянию до источника колебаний – это характерно для сферических волн: 

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)
Волны. Уравнение волны
Волновая природа света
1. Радужные пятна на поверхности воды, покрытой тонкой пленкой бензина, объясняются…
b) интерференцией света
2. Постоянно меняющаяся радужная окраска мыльных пузырей объясняется…
a) интерференцией света
3. Радуга на небе объясняется…
a) дисперсией света
4. При прохождении параллельного пучка белого света через дифракционную решетку наблюдается его разложение в спектр. Это явление объясняется…
d) дифракцией света
Волны. Уравнение волны
1. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси OХ, имеет вид 
( 


a) 3,14
2. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси OХ, имеет вид 
5. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси OХ, имеет вид 
8. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси OХ, имеет вид 
Волны
1. Для плоской волны справедливо утверждение…
b) Амплитуда волны не зависит от расстояния до источника колебаний (при условии, что поглощением среды можно пренебречь).
2. Для сферической волны справедливо утверждение…
b) Амплитуда волны обратно пропорциональна расстоянию до источника колебаний
(в непоглощающей среде).
3. Для поперечной волны справедливо утверждение…
b) Частицы среды колеблются в направлениях, перпендикулярных направлению распространения волны.
4. В газовой среде распространяются…
a) только продольные волны
Дата добавления: 2015-01-30 ; просмотров: 233 | Нарушение авторских прав
Бегущие электромагнитные волны
Уравнение плоской бегущей волны
Если волна движется по О х без поглощения энергии, то это характеризуется уравнением:
Что называют электромагнитной волной. Волновое число
Запись выражения ( 1 ) примет совершенно другой вид при известном волновом числе.
Если перейти к комплексным числам, применив формулу Эйлера, уравнение плоской волны зафиксируем.
Выражение ( 6 ) имеет физический смысл только в действительной части, но R e возможно опустить в записи уравнения волны.
Перейдем к рассмотрению волнового процесса, где не происходит изменение фазы.
При условии, что υ волны зависит от частоты колебаний, то такая волна подвержена дисперсии.
Уравнение сферической бегущей волны
Сферическая волна – это волна, волновая поверхность которой является концентрической сферой. Такое уравнение примет вид:
где r является расстоянием от центра волны до точки рассмотрения. Если имеем дело со сферической волной, то ее амплитуда колебаний не будет постоянной даже при условии, что энергия не поглощается средой. Ее убывание происходит обратно пропорционально расстоянию. Выполнение уравнения ( 8 ) возможно тогда, когда источник волн считается точечным.
Уравнение бегущей волны в любом виде подчинено волновому уравнению.
За основу необходимо принять выражение для амплитуд электромагнитной волны:
Для записи уравнения колебаний H → в электромагнитной волне, в случае если она считается плоской и распространяется по О х :
Необходимо учитывать, что тело, которое поглощает падающую на него энергию, оказывается под давлением, равным среднему значению объемной плотности энергии в электромагнитной волне.
Следует применять соотношение амплитуд электромагнитной волны, которое записывается:
Следует, что значение объемной плотности электрической энергии примет вид:
Формула плотности магнитного поля:
После усреднения плотности, имеем:
Увеличится в 4 раза
1 уменьшится в 2 раза
2 уменьшится в 4 раза
3 увеличится в 4 раза
Увеличится в 2 раза
1 достигнет нового максимума через время T/4
2 достигнет нового максимума через время Т
3 достигнет нового максимума через время 3T/4
Достигнет нового максимума через время T/2
1 больше частоты внешнего воздействия
2 меньше частоты внешнего воздействия
3 увеличивается с течением времени
4 равна частоте свободных колебаний
Равна частоте внешнего воздействия
1 больше собственной частоты системы
2 равна собственной частоте системы
3 уменьшается с течением времени
4 увеличивается с течением времени
Меньше собственной частоты системы
1
2
3
4
1
2
3
4
Сложение гармонических колебаний.
12.1. Складываются два гармонических колебания одного направления с одинаковой частотой и равными амплитудами А0. При разности фаз Δφ=π амплитуда результирующего колебания …
ВАРИАНТЫ ОТВЕТОВ:
12.2.Складываются два гармонических колебания одного направления с одинаковыми периодами и равными амплитудами А0. При разности фаз Δφ=π/2 амплитуда результирующего колебания …
ВАРИАНТЫ ОТВЕТОВ:
12.3. Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз …
ВАРИАНТЫ ОТВЕТОВ:
12.4. Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет минимальную амплитуду при разности фаз …
ВАРИАНТЫ ОТВЕТОВ:
12.5. Складываются два гармонических колебания одного направления с одинаковой частотой и равными амплитудами А0. При разности фаз 
ВАРИАНТЫ ОТВЕТОВ:
1) А0 ; 2) 0 ; 3) 2А0; 4) 
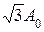


12.6. Складываются два гармонических колебания одного направления с одинаковой частотой и равными амплитудами А0. При разности фаз 
ВАРИАНТЫ ОТВЕТОВ:
1) 
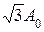


12.7. Складываются два гармонических колебания одного направления с одинаковыми частотами и амплитудами, равными 2А0 и А0. При разности фаз, 
ВАРИАНТЫ ОТВЕТОВ:
1) 

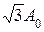

12.8. Складываются два гармонических колебания одного направления с одинаковыми частотами и амплитудами, равными 2А0 и А0. При разности фаз, 
ВАРИАНТЫ ОТВЕТОВ:
1) 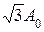



ВАРИАНТЫ ОТВЕТОВ:
1) 




12.10.Точка участвует одновременно в двух одинаково направленных колебаниях, выражаемых уравнениями: 

ВАРИАНТЫ ОТВЕТОВ:
12.11.Точка участвует одновременно в двух одинаково направленных колебаниях, выражаемых уравнениями: 

ВАРИАНТЫ ОТВЕТОВ:
12.12.Складываются два гармонических колебания одного направления с одинаковыми периодами и амплитудами А1=А2=2см. Начальные фазы колебаний 

ВАРИАНТЫ ОТВЕТОВ:
Механические волны.
13.1. Профиль бегущей поперечной волны с периодом колебаний 10 мс представлен на рисунке. Скорость распространения волны в (м/с)равна …
ВАРИАНТЫ ОТВЕТОВ:
13.2. Для продольной волны справедливо утверждение …
ВАРИАНТЫ ОТВЕТОВ:
1) частицы среды колеблются в направлении распространения волны;
2) частицы среды колеблются в направлениях, перпендикулярных направлению
3) возникновение волны связано с деформацией сдвига.
13.3. Продольными волнами являются …
ВАРИАНТЫ ОТВЕТОВ:
1) звуковые волны в воздухе;
2) волны, распространяющиеся вдоль струн музыкальных инструментов;
3) волны на поверхности жидкости;
4) световые волны в вакууме.
13.4. Для плоской бегущей волны справедливо утверждение, что …
ВАРИАНТЫ ОТВЕТОВ:
1) амплитуда волны не зависит от расстояния до источника колебаний (при условии, что поглощением среды можно пренебречь);
2) амплитуда волны обратно пропорциональна расстоянию до источника колебаний (при условии, что поглощением среды можно пренебречь);
3) нет переноса энергии.
13.5. Для поперечной волны справедливо утверждение …
ВАРИАНТЫ ОТВЕТОВ:
1) частицы колеблются в направлении, перпендикулярном направлению распространения волны;
2) частицы колеблются в направлении распространения волны;
3) частицы движутся по кругу в плоскости, параллельной направлению распространения волны;
4) частицы движутся по кругу в плоскости, перпендикулярной направлению распространения волны.
ВАРИАНТЫ ОТВЕТОВ:
1) колебательное вдоль оси Ox ;
2) равномерное по синусоидальной траектории ;
3) равномерное прямолинейное вдоль оси Ox ;
13.7. Звуковые волны в твердом теле могут быть …
ВАРИАНТЫ ОТВЕТОВ:
1) как продольными, так и поперечными;
2) только продольными;
3) только поперечными;
4) только крутильные.
13.8. Звуковые волны какого типа могут распространяться в газах?
ВАРИАНТЫ ОТВЕТОВ:
1) только продольные;
2) только поперечные;
3) продольные и поперечные;
4) никакие не могут.
13.9. В каких упругих средах могут распространяться звуковые продольные волны?
ВАРИАНТЫ ОТВЕТОВ:
1) в газах, жидкостях и твердых телах;
2) только в газах и жидкостях;
3) только в твердых телах;

ВАРИАНТЫ ОТВЕТОВ:
1) 200 ; 2) 400 ; 3) 0,02 ; 4) 0,04 ; 5) 2; 6 ) 4.
13.11. На рисунке представлен профиль бегущей поперечной волны, распространяющейся со скоростью 200 м/c. Циклическая частота волны (в с −1 ) равна.
ВАРИАНТЫ ОТВЕТОВ:
1) 157 ; 2) 125,6 ; 3) 209,3 ; 4) 255 ; 5) 50; 6) 25.
ВАРИАНТЫ ОТВЕТОВ:
Уравнение волны.
14.1. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид 
ВАРИАНТЫ ОТВЕТОВ:
14.2.Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид 
ВАРИАНТЫ ОТВЕТОВ:
14.3. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ со скоростью 500 м/с, имеет вид 
ВАРИАНТЫ ОТВЕТОВ:
14.4. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ со скоростью 500 м/с, имеет вид 
ВАРИАНТЫ ОТВЕТОВ:
14.5. Уравнение плоской волны, распространяющейся в направлении x, имеет вид 
ВАРИАНТЫ ОТВЕТОВ:
14.6. Уравнение плоской волны, распространяющейся в направлении x, имеет вид 
ВАРИАНТЫ ОТВЕТОВ:
ВАРИАНТЫ ОТВЕТОВ:
ВАРИАНТЫ ОТВЕТОВ:
ВАРИАНТЫ ОТВЕТОВ:
ВАРИАНТЫ ОТВЕТОВ:
14.11. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ со скоростью 750 м/с, имеет вид 
ВАРИАНТЫ ОТВЕТОВ:
14.12. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ со скоростью 340м/с, имеет вид 
ВАРИАНТЫ ОТВЕТОВ:
1) 5 ; 2) 0,5 ; 3) 2; 4) 0,2 ; 5) 170 ; 6) 17.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.