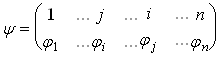
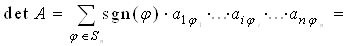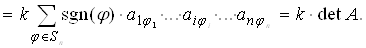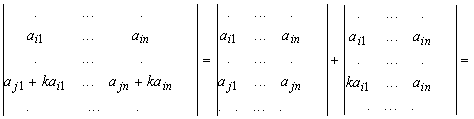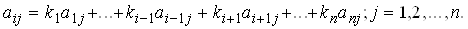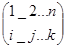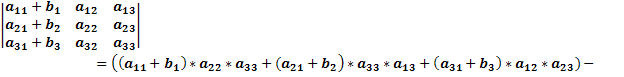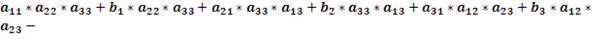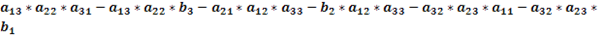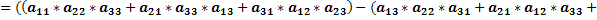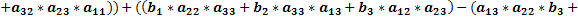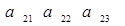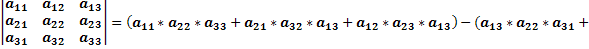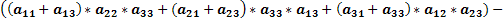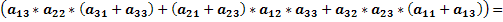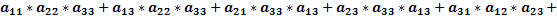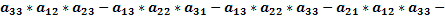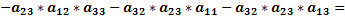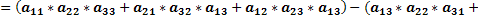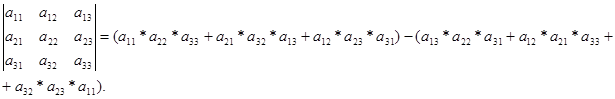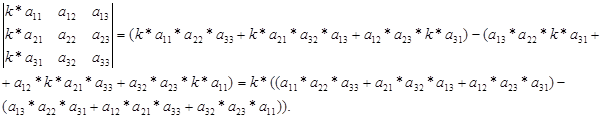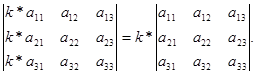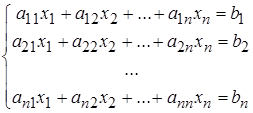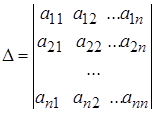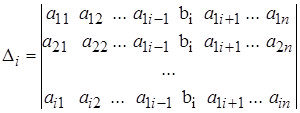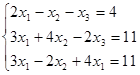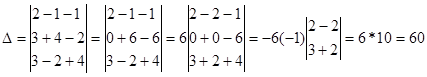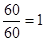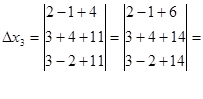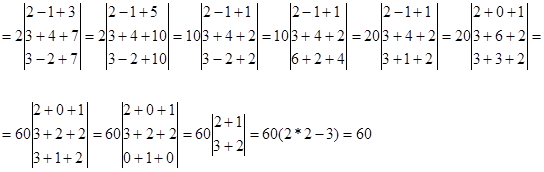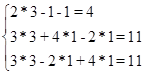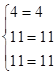Доказать что два определителя равны

08. Свойства определителей

Определение 9. Транспонированием A матрицы называется такое ее преобразование, при котором строки матрицы становятся ее столбцами с теми же самыми номерами.

Матрица транспонированная матрице A обозначается символом :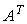

.

Свойство 1. Определитель транспонированной матрицы равен определителю исходной матрицы, т. е. .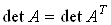

Доказательство. ОПределителя матрицы А есть алгебраическая сумма N! произведений вида

(11)

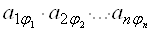
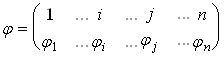
Где в каждое произведение входит по одному элементу из каждой строки и каждого столбца матрицы A, со знаком равным знаку подстановки

.

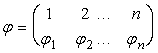
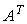
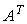
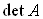
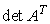
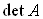
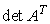
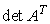
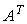
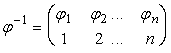
Так как сомножители произведения (11) также находятся по одному в каждом столбце и каждой строке матрицы , то каждое произведение определителя матрицы A входит в определитель матрицы . Отсюда. так как количество слагаемых в и в одинаково, следует, что и в состоят из одних и тех же слагаемых. Для того, чтобы показать, что знаки произведений равны, составим подстановку для произведения (11) в (учитываем, что строки матрицы А стали столбцами матрицы с теми же номерами). Она равна подтановке:

.

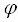
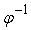
Подстановки иИмеют одинаковое число инверсий, четность и знак.

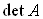
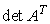
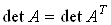
Таким образом и суммы одних и тех же произведений и поэтому . Свойство доказано.

Замечание 1. Из свойства 1 вытекает, что строки и столбцы матрицы Равноправны, т. е., если какое-нибудь свойство доказано для строк, то оно будет справедливо и для столбцов и обратно. Поэтому дальнейшие свойства формулируются и доказываются только для строк. В дальнейшем под строками и столбцами определителя понимаются строки и столбцы соответствующей матрицы.

Свойство 2. Если в матрице поменять местами две строки, то абсолютная величина определителя не меняется, а знак определителя меняется на противоположный.

Доказательство. Пусть даны исходный и преобразованный определитель:

. (12)

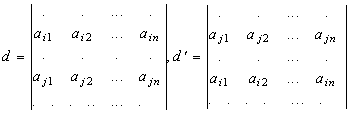
ОПределитель D есть алгебраическая сумма N! произведений вида

, (13)

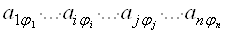
Где в каждое произведение входит по одному элементу из каждой строки и каждого столбца определителя D, со знаком равным знаку подстановки

.

Свойство 3. Если в определителе есть две одинаковые строки, то определитель равен нулю.

Свойство 4. Если в определителе есть нулевая строка, то определитель равен нулю.

Доказательство. Пусть в определителе I-я строка нулевая. По определению определителя он равен алгебраической сумме произведений вида:

.

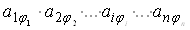
В каждое произведение входит нулевой элемент I-й строки и поэтому оно равно нулю. Следовательно, и определитель равен нулю. Свойство доказано.

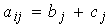
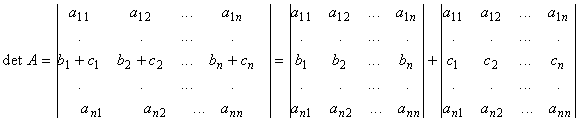
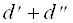
Пусть все элементы I-й строки представлены в виде ; J=1,2. N. Тогда свойство перепишется в виде:

=

= .

Доказательство. По формуле (8) находим

= .

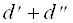
Замечание 2. Индукцией по m легко доказать, что свойство 5 справедливо для случая, когда каждый элемент i-й строки сумма m слагаемых, .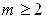

Свойство 6. Если все элементы какой-нибудь строки определителя имеют общий множитель, то его можно вынести за знак определителя, т. е., если элементы какой-нибудь строки определителя умножить на число k, то и сам определитель умножится на число k.

.

Доказательство. По формуле (8) находим

Свойство 7. Если в определителе есть две пропорциональны строки, то он равен нулю.

Доказательство. Пусть I-я и J-я строки определителя пропорциональны, т. е. 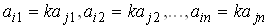. Вынося из J-й общий множитель K за знак определителя, получим определитель с двумя равными строками, который равен нулю. Поэтому и исходный определитель равен нулю. Свойство доказано.

Свойство 8. Если к какой-нибудь строке определителя прибавить другую строку, умноженную на число k, то определитель от этого не изменится.

Определение 10. Говорят, что I-я строка матрицы A есть линейная комбинация остальных строк определителя, если существуют такие числа 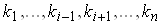, что каждый элемент I-й строки есть сумма попарных произведений этих чисел на соответствующие элементы остальных строк матрицы, т. е.

Свойство 9. Если какая-нибудь строка определителя есть линейная комбинация остальных строк определителя, то определитель равен нулю.

Доказательство. Если I-я строка определителя есть линейная комбинация остальных строк определителя, то по замечанию 2 определитель равен сумме n-1 определителей с пропорциональными строками, и по свойству 7 все такие определители равны нулю. Тогда и исходный определитель равен нулю. Свойство доказано.

Источник

Доказать что два определителя равны

Доказательство проводится проверкой, т.е. сравнением обеих частей записанного равенства. Вычислим определители, стоящие слева и справа:

Доказательство проводится аналогично доказательству свойства 1 сравнением обеих частей. Проведём его для определителя второго порядка.

.

Для определителя третьего порядка проверьте самостоятельно.

Действительно, если переставить здесь 2-ю и 3-ю строки, то по свойству 2 этот определитель должен изменить знак, но сам определитель в данном случае не меняется, т.е. получаем |A| = –|A| или |A| = 0.

Доказательство проводится проверкой, как и свойство 1. (Самостоятельно)

.

.

Докажем это равенство, используя предыдущие свойства определителя.

Эти свойства определителей довольно часто используются при вычислении определителей и в различных задачах.

АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ И МИНОРЫ

Пусть имеем определитель третьего порядка: .

Минором, соответствующим данному элементу a_ij определителя третьего порядка, называется определитель второго порядка, полученный из данного вычёркиванием строки и столбца, на пересечении которых стоит данный элемент, т.е. i-ой строки и j-го столбца. Миноры соответствующие данному элементу a_ij будем обозначать M_ij.

Например, минором M₁₂, соответствующим элементу a₁₂, будет определитель , который получается вычёркиванием из данного определителя 1-ой строки и 2-го столбца.

Таким образом, формула, определяющая определитель третьего порядка, показывает, что этот определитель равен сумме произведений элементов 1-ой строки на соответствующие им миноры; при этом минор, соответствующий элементу a₁₂, берётся со знаком “–”, т.е. можно записать, что

.

(1)

Аналогично можно ввести определения миноров для определителей второго порядка и высших порядков.

Введём ещё одно понятие.

Алгебраическое дополнение элемента a_ij обозначается A_ij.

Из определения получаем, что связь между алгебраическим дополнением элемента и его минором выражается равенством A_ij = (–1) i+j M_ij.

Например,

Пример. Дан определитель . Найти A₁₃, A₂₁, A₃₂.

Легко видеть, что используя алгебраические дополнения элементов, формулу (1) можно записать в виде:

.

Аналогично этой формуле можно получить разложение определителя по элементам любой строки или столбца.

Например, разложение определителя по элементам 2-ой строки можно получить следующим образом. Согласно свойству 2 определителя имеем:

Разложим полученный определитель по элементам 1-ой строки.

.

(2)

Отсюда т.к. определители второго порядка в формуле (2) есть миноры элементов a₂₁, a₂₂, a₂₃. Таким образом, , т.е. мы получили разложение определителя по элементам 2-ой строки.

Аналогично можно получить разложение определителя по элементам третьей строки. Используя свойство 1 определителей (о транспонировании), можно показать, что аналогичные разложения справедливы и при разложении по элементам столбцов.

Таким образом, справедлива следующая теорема.

Теорема (о разложении определителя по заданной строке или столбцу). Определитель равен сумме произведений элементов какой–либо его строки (или столбца) на их алгебраические дополнения.

Всё вышесказанное справедливо и для определителей любого более высокого порядка.

ОБРАТНАЯ МАТРИЦА

Понятие обратной матрицы вводится только для квадратных матриц.

Справедлива следующая теорема:

Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.

Прежде всего заметим, что можно доказать следующее свойство определителей .

Предположим, что |A| = 0. Тогда . Но с другой стороны . Полученное противоречие и доказывает, что |A| ≠ 0.

Покажем, что в этом случае обратной матрицей будет матрица

, где A_ij алгебраическое дополнение элемента a_ij.

Заметим, что все диагональные элементы матрицы C будут равны 1. Действительно, например,

Аналогично по теореме о разложении определителя по элементам строки можно доказать, что c₂₂ = c₃₃ = 1.

Кроме того, все недиагональные элементы матрицы C равны нулю. Например,

Таким образом, теорема содержит способ нахождения обратной матрицы.

Если условия теоремы выполнены, то матрица обратная к матрице находится следующим образом

,

Итак, чтобы найти обратную матрицу нужно:

Аналогично для матриц второго порядка, обратной будет следующая матрица .

|A| = 2. Найдем алгебраические дополнения элементов матрицы A.

.

.

Вычислим |A| = 4. Тогда .

.

Источник

Доказательства свойств определителя

Свойство №1: Определитель не изменяется при транспортировании матриц (строк и столбцов).

Доказательство:

Опр. Матрицы A_ji называется транспонированной матрицей A_ij

= det A = det A T

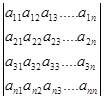
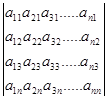
Выберем любое слагаемое из суммы определителя.

Следовательно определители равны.

Свойство №2: Если один из столбцов (строк) состоит из нулей, то определитель равен нулю.

Доказательство:

Пусть дана матрица, один столбец которой равен 0.

=detA подсчитаем определитель данной матрицы.

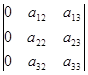
Подсчитаем определитель данной матрицы, используя правило равнобедренных треугольников, основания которых параллельны главной и побочной диагоналям.

=0*а₂₂*а₃₃+а₁₂*а₂₃*0+а₃₂*а₁₃*0 = 0

=-(а₁₃*а₂₂*0+а₁₂*а₃₃*0+а₂₃*а₃₂*0)=0

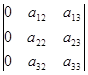
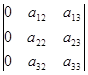
Свойство №3: Если один из определителей получен из другого определителя перестановкой двух столбцов (строк), то определители отличаются друг от друга знаком.

Доказательство:Возьмём матрицу определитель которой равен detA и переставим в ней 2 столбца. Получим:

,после перестановки получим: .

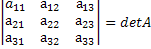
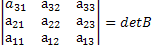
Посчитаем определители обеих матриц. Получим:

Получили, что det A=-det B.

Свойство №4: Если все элементы какого-либо i-го столбца (строки) определителя являются суммами двух слагаемых, то такой определитель равен сумме двух определителей в первом из которых в качестве i-го столбца (строки) взяты первые слагаемые, а во втором – вторые слагаемые; при этом элементы всех остальных строк (столбцов) у каждого из трёх определителей одинаковы.

Доказательство:

Возьмём матрицу, в которой элементы первого столбца равны a_ij+b_j и посчитаем её определитель.

.

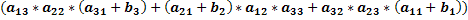
Раскроем скобки и приведём подобные слагаемые.

.

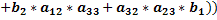
То есть: .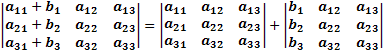

Свойство №5: Определитель, содержащий два пропорциональных, в частности два равных, столбца (строки), равен нулю.

Доказательство:

Пусть дан определитель detA≠0, содержащий две равные строки.

= detA ; =

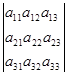
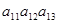
Поменяем местами эти равные строки. Получим новый определитель.

.

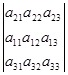
Так как данный определитель получен из определителя detA перестановкой строк, то из предыдущего свойства следует, что полученный определитель принимает значение –detA. В то же время, количество слагаемых и модуль значений определителей detA и –detA равны, то справедливо будет равенство detA=-detA. Из данного равенства следует что detA=0. Свойство доказано.

Свойство №6: Определитель не меняется, если к какому-нибудь столбцу (строке) прибавить линейную комбинацию других столбцов (строк).

Доказательство:

Возьмём матрицу коэффициентов и посчитаем её определитель.

Прибавим к первому столбцу третий. Получим новую матрицу.

.

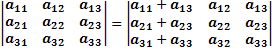
Посчитаем её определитель.

.

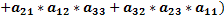
Свойство №7: Если все элементы какого-нибудь столбца (строки) определителя умножить на некоторое число k, то есть весь определитель умножается на k, то общий множитель любой строки или любого столбца можно выносить за знак определителя.

Доказательство:Возьмём матрицу и посчитаем её определитель.

То есть.

5. Пример применения правила Крамера для решения систем n уравнений с n неизвестными

Определители очень широко используются при решении и исследовании систем линейных n уравнений с n неизвестными. Правило решения такой системы с помощью определителей называется правилом Крамера. Покажем это правило на примере.

Правило Крамера: правило решения системы n линейных уравнений. с n неизвестными, определитель которой отличен от нуля, всегда имеет решение. Это решение единственное и определяется таким правилом Крамера: значение каждого из неизвестных 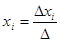, где — определитель системы., матрица которого составлена из коэффициентов при неизвестных системы, а _I – определитель, матрица которого получена заменой столбца коэффициентов при данном неизвестном на столбец свободных членов системы. В случае если определитель системы равен нулю, система имеет бесконечно много решений.

Пусть дана система из трех уравнений с тремя неизвестными:

Посчитаем определитель матрицы системы, составленной из коэффициентов при неизвестных:

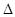
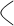
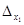
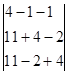
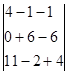
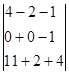
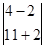
После подсчета определителя системы, подсчитаем определители неизвестных. Для этого вырезаем из столбец данной переменной, а на его место ставим столбец свободного члена.

= = = 6 = 6 = 6*(4*2-(-2)*11)=180

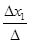
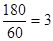
Согласно правилу Крамера значение неизвестной переменной равно частному от определителя данной неизвестной и определителя системы. Значит переменная x_{1= ;} x₁= .

Действуя по тому же алгоритму, найдем значения переменных x₂ и x₃:

По правилу равнобедренных треугольников, основания которых параллельны главной и побочной диагоналям матрицы получим:

= 2*11*4+3*11*(-1)+4*(-2)*3= 88-33-24=31 =60

-2*(-2)*11-3*4*4 – (-1)*11*3= 44-48+33=29

Значит x₂=

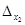
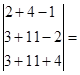
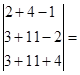
Значит x₃=

Для доказательства истинности правила Крамера, проверим полученные значения переменных, подставив полученные значения в систему:

После подстановки мы получили верное числовое равенство, значит, правило Крамера истинно для решения системы n уравнений с n неизвестными. Ответ: (3;1;1)

Глава 2.Векторное произведение

Источник