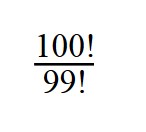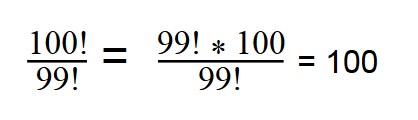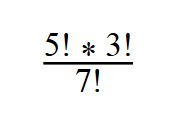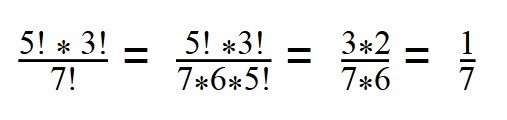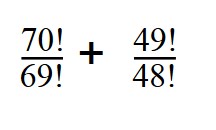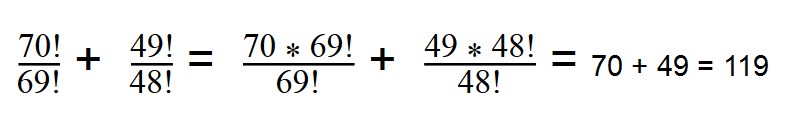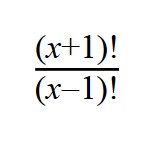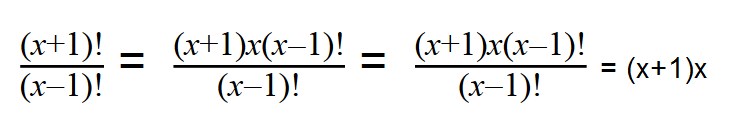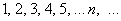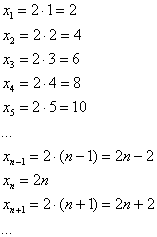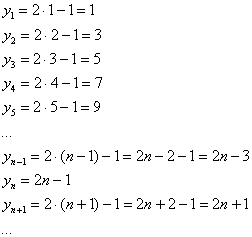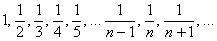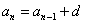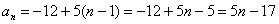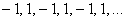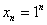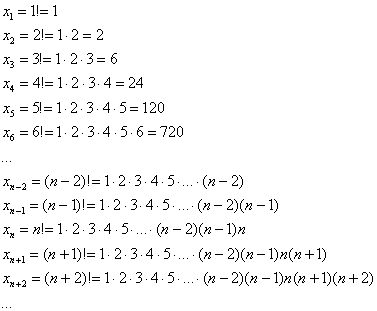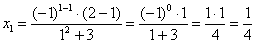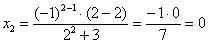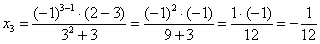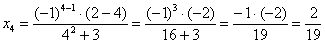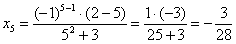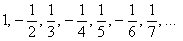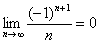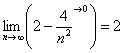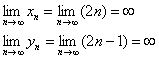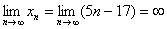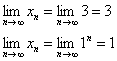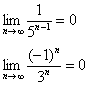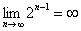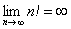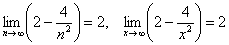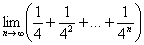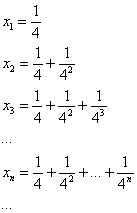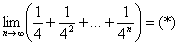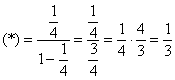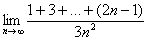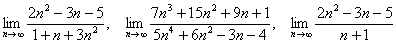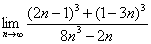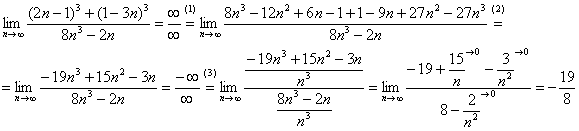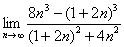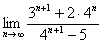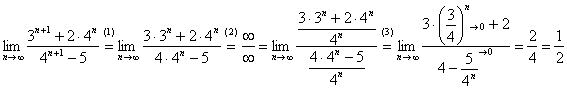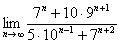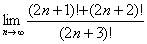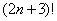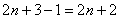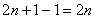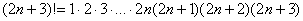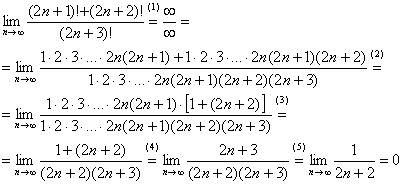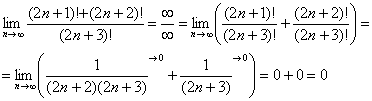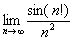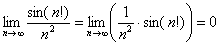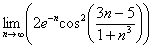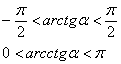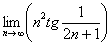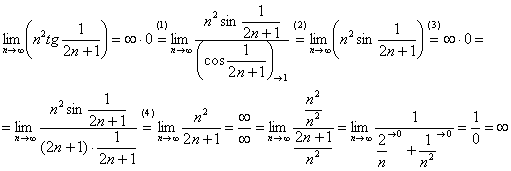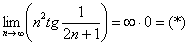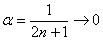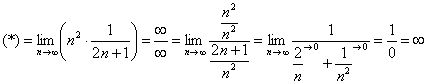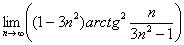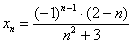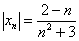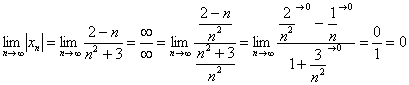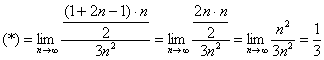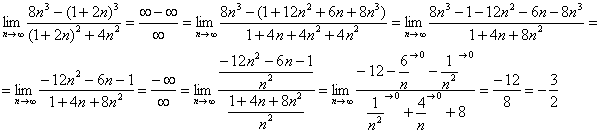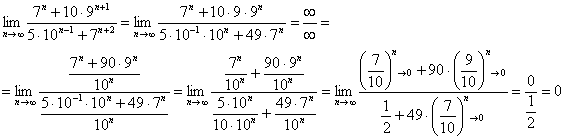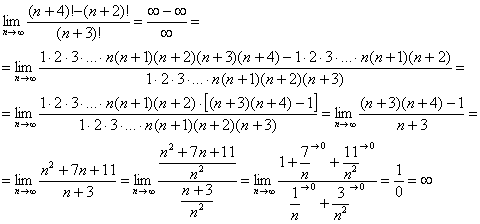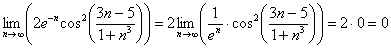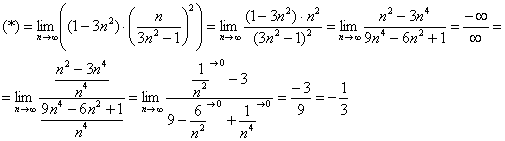Доказать что факториал растет быстрее показательной функции
Вопрос по Главе 7. Задача про скорость роста функций
Расположите следующие 4 функции в порядке увеличения скорости роста (каждая функция есть O(следующая)), не исключено, что некоторые функции имеют одинаковую скорость
1) f1(n) = n!;
2) f2(n) = n2;
3) f3(n) = ln n ;
4) f4(n) = n(ln n).
А поясните, пожалуйста, почему Вы так считаете? Спасибо
1. Любой полилогарифм растет быстрее любого полинома. Значит, ln n=O(n). Следовательно, ln n=O(n (ln n)), т.к. n (ln n) растёт ещё быстрее, чем n.
2. Из ln n=O(n) также следует, что n(ln n)=O(n^2).
3. Факториал по скорости роста обгоняет даже показательную функцию, а любая показательная функция растёт быстрее полинома. Значит, n^2=O(n!). Можно ещё следующим образом показать, что факториал «больше» полинома. Чем выше степень полинома, тем он быстрее растёт. Например, n^2=O(n^3), n^3=O(n^5) и т.д. Представим факториал в виде произведения: n!=n*(n-1)*(n-2)*. *1. Если раскрыть первые 3 скобки, мы уже получим функцию, «не меньшую» чем n^3. Следовательно, т.к. n^2=O(n^3), то n^2=O(n!).
Ольга, но ведь n * (ln n) растёт в n раз быстрее, чем ln n.
Кроме того, где сравнение функций ln n и n * (ln n) с функцией n!?
Т.к. n^2=O(n!) и n*ln n=O(n^2), то n*ln n=O(n!).
Т.к. n*ln n=O(n!) и ln n=O(n*ln n), то ln n=O(n!).
Отношение «расти быстрее» транзитивно, поэтому сравнивать функции, которые «меньше» n^2, с факториалом особого смысла нет.
По поводу первого замечания: n * (ln n) действительно растет быстрее, чем ln n. Только я не поняла, к чему данное замечание относилось. Поясните, пожалуйста.
Значит, в Вашем первом ответе опечатка,
А по условиям задачи мы умеем следующее:
Следовательно, в Вашем ответе функция ln n растёт быстрее, чем n(ln n).
А про факториал, поправьте пожалуйста, если не прав, я читал, что это самая быстро растущая функция.
В моём ответе всё верно. В задании просят расположить функции в порядке увеличения скорости роста, т.е. ln n, n*ln n, n^2, n!, или f3, f4, f2, f1.
Поправка: в данном случае речь идёт о множестве не действительных чисел, а натуральных.
Другое дело, что скорость роста n! не слишком хороша для сравнения, и не очень понятно, где ее можно использовать. Удобнее пользоваться показательной функцией (экспонентой).
Извините, для какого сравнения не слишком хороша скорость роста факториала?
Тут я ошибся, переклинило и я решал обратную задачу, вот и всё. выше про это уже извинялся.
EugenO, не согласен, мы же смотрим не значения в точках, а скорость роста функции.
Или же, поясните подробнее, в чём именно на Ваш взгляд выражено это не удобство в сравнении.
Для меня удобство экспоненты в том, что она очень хороша для анализа. Она легко представима в виде a^x, элементарно дифференцируема (скорость роста) и интегрируема, причем многократно, связана со вторым замечательным пределом, кроме того, интуитивно (для меня) понятна, я ее график много раз рисовал в детстве и с удовольствием ассоциирую с всевозможными процессами, происходящими в реальной жизни, поэтому вижу естественным применение в асимптотике. В то же время не смогу указать ни одного естественного инерционного процесса, который изменялся бы «со скоростью выше экспоненциальной». Кстати, известна Stirling’s approximation для оценки факториала, а оценки экспоненты через факториал что-то не припомню (наверное, в ней смысла нет).
Хотелось бы узнать, зачем при анализе сложности алгоритмов Вы дифференцируете, интегрируете (причем многократно) экспоненту, как используете второй замечательный предел и формулу Стирлинга. Я не отрицаю, что, возможно, в теории сложности вычислений без этого нельзя обойтись. К сожалению, в данной области у меня очень скромный опыт((. А Вы, наверное, в этом вопросе отлично разбираетесь (может, даже на профессиональном уровне!). Поэтому очень интересно посмотреть, как применяет математический, комплексный и функциональный анализы в асимптотике настоящий специалист. Приведите, пожалуйста, пример.
Факториал
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Факториал: определение
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».
Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:
Число должно быть целое и положительное:
Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.
Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6
Формулы и свойства факториала
Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.
| 1! = 1 |
| 2! = 2 |
| 3! = 6 |
| 4! = 24 |
| 5! = 120 |
| 6! = 720 |
| 7! = 5040 |
| 8! = 40320 |
| 9! = 362880 |
| 10! = 3628800 |
| 11! = 39916800 |
| 12! = 479001600 |
| 13! = 6227020800 |
| 14! = 87178291200 |
| 15! = 1307674368000 |
| 16! = 20922789888000 |
| 17! = 355687428096000 |
| 18! = 6402373705728000 |
| 19! = 121645100408832000 |
| 20! = 2432902008176640000 |
| 21! = 51090942171709440000 |
| 22! = 1124000727777607680000 |
| 23! = 25852016738884976640000 |
| 24! = 620448401733239439360000 |
| 25! = 15511210043330985984000000 |
Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:
С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.
Такая формула дает результат с небольшой погрешностью.
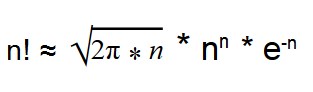 |
Рекуррентная формула
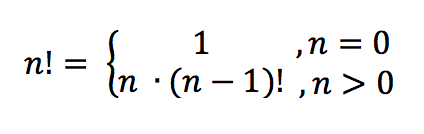 |
Для решения примеров обращайтесь к таблице.
Примеры умножения факториалов:
Примеры решений
Давайте поупражняемся и решим пару примеров.
1. Сократите дробь:
Далее сокращаем по принципу сокращения обыкновенных дробей.
2. Вычислите значение выражения с факториалом: 8! + 5!
Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.
А можно потренироваться и разложить их:
8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440
3. Вычислите значение выражения:
7! = 1*2*3*4*5*6*7 = 5! * 6 *7
Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.
4. Вычислите значение выражение:
Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*. *69 = 69! * 70
49! = 1*2*3*. 49! * 48
Далее сокращаем все одинаковые множители.
5. Сократите дробь:
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.
Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.
Что растет быстрее Факториал или степенная функция?
Факториал по скорости роста обгоняет даже показательную функцию, а любая показательная функция растёт быстрее полинома. Значит, n^2=O(n!).
Какая из функций растёт быстрее N или n2?
растет быстрее, чем 2^n.
Что растет быстрее Факториал или X X?
функция xx растет еще быстрее факториала.
Что такое 5 Факториал?
| n | n! |
|---|---|
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
Чему равен 1 Факториал?
Определяется она следующим образом: F (0) = F (1) = 1; F (n) = n * F (n-1). По общепринятой договоренности 0! = 1 (факториал нуля равен единице). приблизительно равен 2.28803779534.
Что растет быстрее n или n n?
По поводу первого замечания: n * (ln n) действительно растет быстрее, чем ln n.
Что растет быстрее логарифм и корень?
Сравнивая обе величины, мы заключаем, что вторая из них больше, так как корень растёт быстрее логарифма, и потому корень из логарифма растёт быстрее двойного логарифма.
Что растет быстрее логарифм и степенная?
Показательная функция растет быстрее степенной, а степенная – быстрее логарифмической.
Ещё бы доказательство такое же простое почему 0 в 0-й степени равно 1 🙂 По аналогии 00 = сколько раз «ничего» встречается в «ничего» = тоже лишь 1 раз. Кстати, есть альтернативная точка зрения, при которой принято считать что значение 0 в 0-й степени неопределено.
Как правильно посчитать факториал?
Факториалом числа называют произведение всех натуральных чисел до него включительно. Например, факториал числа 5 равен произведению 1 * 2 * 3 * 4 * 5 = 120.
Для чего используется Факториал?
Факториал очень активно используется в различных разделах математики, особенно там, где заходит речь о различных вариантах, перестановках, комбинациях и т. п. Он применяется в комбинаторике, теории чисел, математическом анализе и других областях.
Что такое Факториал определение?
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал». Факториал определен для целых неотрицательных чисел.
Что делает Факториал?
Слово факториал произошло от латинского factor (делающий, производящий). Факториал числа — это произведение натуральных чисел от 1 до самого числа (включая данное число). … Обозначается факториал восклицательным знаком «!».
Сколько будет 50 Факториал?
В таблице приведены значения факториалов для чисел от 0 до 50.
| число | факториал числа |
|---|---|
| 48! | 12413915592536072670862289047373375038521486354677760000000000 |
| 49! | 608281864034267560872252163321295376887552831379210240000000000 |
| 50! | 30414093201713378043612608166064768844377641568960512000000000000 |
Что такое 100 Факториал?
Из сомножителей факториала 100 десять заканчиваются на ноль: 10, 20, 30, 40, 50, 60, 70, 80, 90 и 100 (заканчивается на два 0). Это дает уже как минимум одиннадцать конечных нулей, которые 100! … Все, кроме последней пары, входят в сотню составляющих факториала 100.
Можно ли сократить Факториал?
В дроби равные факториалы можно сокращать).
Числовая последовательность.
Как найти предел последовательности?
На данном уроке мы узнаем много интересного из жизни участников большого сообщества под названием Вконтакте числовые последовательности. Рассматриваемая тема относится не только к курсу математического анализа, но и затрагивает основы дискретной математики. Кроме того, материал потребуется для освоения других разделов вышки, в частности, в ходе изучения числовых рядов и функциональных рядов. Можно банально сказать, что это важно, можно ободряюще сказать, что это просто, можно сказать ещё много дежурных фраз, однако сегодня первая, необыкновенно ленивая учебная неделя, поэтому меня жутко ломает сочинять первый абзац =) Уже в сердцАх сохранил файл и собрался спать, как вдруг… голову озарила идея чистосердечного признания, которое невероятно облегчило душу и подтолкнуло к дальнейшему стуку пальцами по клавиатуре.
Отвлечёмся от летних воспоминаний, и заглянем в этот увлекательный и позитивный мир новой социальной сети:
Понятие числовой последовательности
Сначала задумаемся над самим словом: а что такое последовательность? Последовательность – это когда что-то расположено за чем-то. Например, последовательность действий, последовательность времён года. Или когда кто-то расположен за кем-то. Например, последовательность людей в очереди, последовательность слонов на тропе к водопою.
Немедленно проясним характерные признаки последовательности. Во-первых, члены последовательности располагаются строго в определённом порядке. Так, если двух человек в очереди поменять местами, то это уже будет другая последовательность. Во-вторых, каждому члену последовательности можно присвоить порядковый номер:
С числами всё аналогично. Пусть каждому натуральному значению 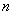
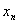
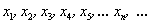
Да, в математических задачах в отличие от жизненных ситуаций последовательность почти всегда содержит бесконечно много чисел.
При этом:
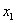
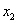
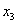
…
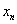
…
На практике последовательность обычно задаётся формулой общего члена, например:
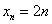
Таким образом, запись 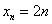
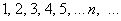
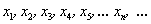
Последовательность положительных нечётных чисел 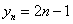
Ещё одна распространённая последовательность 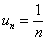
Как, наверное, многие подметили, переменная «эн» играет роль своеобразного счётчика.
На самом деле с числовыми последовательностями мы имели дело ещё в средних классах школы. Вспомним арифметическую прогрессию. Определение переписывать не буду, коснёмся самой сути на конкретном примере. Пусть 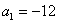
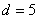
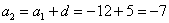
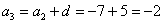
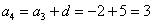
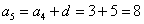
…
И, очевидно, энный член задаётся рекуррентной формулой
Примечание: в рекуррентной формуле каждый следующий член выражается через предыдущий член или даже через целое множество предыдущих членов.
Полученная формула малопригодна на практике – чтобы добраться, скажем, до 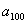
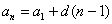
Подставьте в формулу 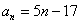
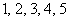
Аналогичные выкладки можно провести для геометрической прогрессии, энный член которой задаётся формулой 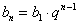
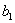
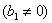
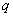
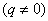
прогрессия 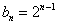
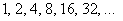
прогрессия 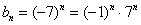
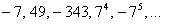
прогрессия 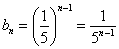
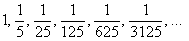
прогрессия 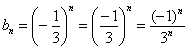
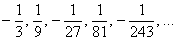
Надеюсь, все знают, что –1 в нечётной степени равно –1, а в чётной – единице.
Прогрессию называют бесконечно убывающей, если 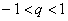
Давайте добавим в свой список двух новых друзей, один из которых только что постучался в матрицу монитора:
Последовательность 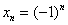
Таким образом, члены последовательности могут повторяться. Так, в рассмотренном примере последовательность состоит из двух бесконечно чередующихся чисел.
А бывает ли так, что последовательность состоит из одинаковых чисел? Конечно. Например, 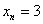
Факториал: 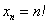
Всего лишь свёрнутая запись произведения:
Отнюдь не графомания, пригодится для задач 😉 Рекомендую осмыслить-запомнить и даже переписать в тетрадь. …Пришёл тут в голову один вопрос: а почему никто не создаёт такие полезные граффити? Едет себе человек в поезде, смотрит в окно и изучает факториалы. Панки отдыхают =)
Возможно, некоторым читателям всё-таки ещё не до конца понятно, как расписать члены последовательности, зная общий член. Тот редкий случай, когда контрольный выстрел возвращает к жизни:
Разберёмся с последовательностью 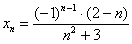
Сначала подставим в энный член значение 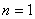
Далее подставим в общий член 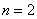
Потом подставим следующий номер 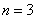
Четвёрку:
Чего уж, теперь и отличную отметку не зазорно заработать:
и так далее… пока разогреется самый последний чайник!
Понятие предела последовательности. Простейшие примеры
Для лучшего осмысления нижеследующей информации желательно ПОНИМАТЬ, что такое предел функции. Конечно, в стандартном курсе математического анализа сначала рассматривают предел последовательности и только потом предел функции, но дело в том, что о самой сущности предела я уже подробно рассказывал. Более того, в теории числовая последовательность считается частным случаем функции, и людям, которые знакомы с пределом функции, будет заметно веселее.
Впрочем, дальше могут читать все-все-все, однако если у вас возникнет непонимание или недопонимание чего-либо, то, пожалуйста, начните с пределов функций.
Пригласим на танец незамысловатую подругу 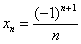
Что происходит, когда «эн» увеличивается до бесконечности? Очевидно, что члены последовательности будут бесконечно близко приближаться к нулю. Это и есть предел данной последовательности, который записывается следующим образом:
Если предел последовательности равен нулю, то её называют бесконечно малой.
В теории математического анализа даётся строгое определение предела последовательности через так называемую эпсилон-окрестность. Этому определению будет посвящёна следующая статья, а пока что разберём его смысл:
Изобразим на числовой прямой члены последовательности 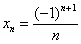
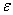
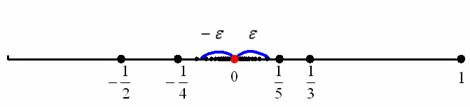
Теперь зажмите синюю окрестность рёбрами ладоней и начинайте её уменьшать, стягивая к пределу (красной точке). Число 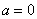
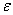
Последовательность 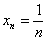
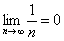
Естественно, предел может быть равен и любому другому конечному числу, элементарный пример:
Здесь дробь стремится к нулю, и соответственно, предел равен «двойке».
Если у последовательности 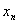
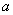
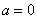
Последовательности 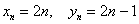
Арифметическая прогрессия с первым членом 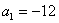
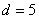
К слову, расходится и любая арифметическая прогрессия, за исключением случая с нулевым шагом – когда к конкретному числу 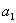
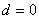
У последовательностей 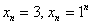
Любая бесконечно убывающая геометрическая прогрессия, как ясно уже из названия, бесконечно малА:
Если знаменатель геометрической прогрессии 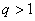
Если же 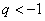
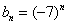
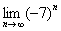
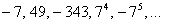
После небольшого разоблачения 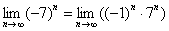
Действительно, для последовательности 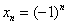
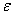
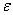
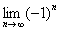
Факториал 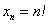
Причём, растёт он как на дрожжах, так, 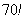
С контрольным выстрелом всё чуть сложнее, и мы как раз подошли к практической части лекции, в которой разберём боевые примеры:
Как найти предел последовательности?
А вот сейчас необходимо уметь решать пределы функций, как минимум, на уровне двух базовых уроков: Пределы. Примеры решений и Замечательные пределы. Потому что многие методы решения будут похожи. Но, прежде всего, проанализируем принципиальные отличия предела последовательности от предела функции:
В пределе последовательности «динамическая» переменная «эн» может стремиться только к «плюс бесконечности» – в сторону увеличения натуральных номеров 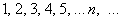
В пределе функции «икс» может быть направлен куда угодно – к «плюс/минус бесконечности» либо к произвольному действительному числу.
Последовательность дискретна (прерывна), то есть состоит из отдельных изолированных членов. Раз, два, три, четыре, пять, вышел зайчик погулять. Для аргумента же функции характерна непрерывность, то есть «икс» плавно, без приключений стремится к тому или иному значению. И, соответственно, значения функции будут так же непрерывно приближаться к своему пределу.
По причине дискретности в пределах последовательностей встречаются свои фирменные вещи, такие как факториалы, «мигалки», прогрессии и т.п. И сейчас я постараюсь разобрать пределы, которые свойственны именно для последовательностей.
Начнём с прогрессий:
Найти предел последовательности
Решение: нечто похожее на бесконечно убывающую геометрическую прогрессию, но она ли это? Для ясности распишем несколько первых членов:
Так как 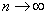
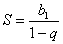
Используем формулу суммы бесконечно убывающей геометрической прогрессии: 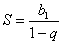
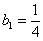
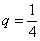
Главное, совладать с четырёхэтажностью дроби:
Написать первые четыре члена последовательности и найти её предел
Это пример для самостоятельного решения. Для устранения неопределённости 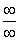
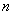
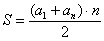
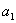
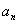
Поскольку в пределах последовательностей «эн» всегда стремится к «плюс бесконечности», то неудивительно, что неопределённость 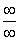
И многие примеры решаются точно так же, как пределы функций!
Как вычислить эти пределы? Смотрите Примеры № 1-3 урока Пределы. Примеры решений.
А может быть что-нибудь посложнее наподобие 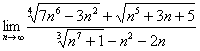
С формальной точки зрения разница будет лишь в одной букве – там «икс», а здесь «эн».
Приём тот же – числитель и знаменатель надо разделить на «эн» в старшей степени.
Также в пределах последовательностей достаточно распространена неопределённость 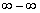
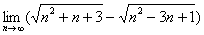
Чтобы разобраться с пределом 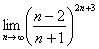
Следующие четыре примера (№ 3-6) тоже «двулики», но на практике почему-то больше характерны для пределов последовательностей, чем для пределов функций:
Найти предел последовательности
Решение: сначала полное решение, потом пошаговые комментарии:
(1) В числителе дважды используем формулу 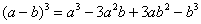
(2) Приводим подобные слагаемые в числителе.
(3) Для устранения неопределённости делим числитель и знаменатель на 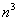
Как видите, ничего сложного.
Найти предел последовательности
Это пример для самостоятельного решения, формулы сокращенного умножения в помощь.
В пределах с показательными последовательностями применяется похожий метод деления числителя и знаменателя:
Найти предел последовательности
Решение оформим по той же схеме:
(1) Используя свойства степеней, вынесем из показателей всё лишнее, оставив там только «эн».
(2) Смотрим, какие показательные последовательности есть в пределе: 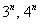
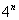
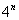
(3) В числителе и знаменателе проводим почленное деление. Поскольку 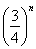
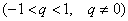
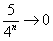
Найти предел последовательности
Это пример для самостоятельного решения.
Как-то незаслуженно остался в забвении стильный почерк, присущий только пределу последовательности. Пора исправить ситуацию:
Найти предел последовательности
Решение: чтобы избавиться от «вечного соперника» 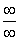
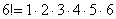
Последним множителем в произведении идёт шестёрка. Что нужно сделать, чтобы получить предыдущий множитель? Вычесть единицу: 6 – 1 = 5. Чтобы получить множитель, который располагается ещё дальше, нужно из пятёрки ещё раз вычесть единичку: 5 – 1 = 4. И так далее.
Не беспокойтесь, это не урок в первом классе коррекционной школы, на самом деле мы знакомимся с важным и универсальным алгоритмом под названием «как разложить любой факториал». Давайте разделаемся с самым злостным флудером нашего чата:
Очевидно, что последним множителем в произведении будет 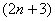
Как получить предыдущий множитель? Вычесть единицу:
Как достать прадедушку? Ещё раз вычесть единицу: 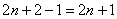
Ну и ещё на один шаг продвинемся вглубь:
Таким образом, наше чудовище распишется следующим образом:
С факториалами числителя всё проще, так, мелкие хулиганы.
Оформляем решение:
(1) Расписываем факториалы
(2) В числителе ДВА слагаемых. Выносим за скобки всё, что можно вынести, в данном случае это произведение 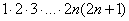
(3) Сокращаем числитель и знаменатель на 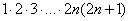
(4) Упрощаем числитель
(5) Сокращаем числитель и знаменатель на 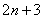
Более подготовленные студенты, которые легко раскладывают факториалы в уме, могут решить пример значительно быстрее. На первом шаге делим почленно числитель на знаменатель и мысленно выполняем сокращения:
Но способ с разложением всё-таки более основателен и надёжен.
Найти предел последовательности
Это пример для самостоятельного решения.
Желающие набить руку на рассмотренных типах пределов могут обратиться к сборнику Кузнецова. Около 150 прорешанных примеров можно найти здесь >>> (задачи № 2-6).
Как и в любом обществе, среди числовых последовательностей попадаются экстравагантные личности.
Теорема: произведение ограниченной последовательности на бесконечно малую последовательность – есть бесконечно малая последовательность.
Если вам не очень понятен термин «ограниченность», пожалуйста, изучите статью об элементарных функциях и графиках.
Аналогичная теорема справедлива, кстати, и для функций: произведение ограниченной функции на бесконечно малую функцию – есть бесконечно малая функция.
Найти предел последовательности
Решение: последовательность 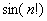
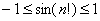
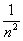
Просто и со вкусом. Да-да, так и оформляем.
Найти предел последовательности
Это пример для самостоятельного решения.
Ещё две распространённые ограниченные функции – арктангенс и арккотангенс:
Аргументы перечисленных тригонометрических функций могут быть заполнены знатной абракадаброй, но это не должно приводить в панику – существенно то, что последовательности ограничены!
Иногда в ходе вычисления пределов последовательностей приходится использовать довольно неожиданные приёмы:
Найти предел последовательности
Решение: неопределённость 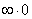
(1) Используем формулу 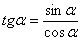
(2) Избавляемся от косинуса, указывая, что он стремится к единице.
(3) Неопределённость 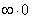
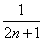
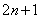
(4) Используем первый замечательный предел 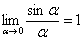
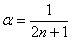
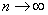
Прокатывает и 2-й метод решения – через замечательные эквивалентности:
Заменим бесконечно малую последовательность эквивалентной:
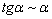
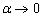
В данном случае
Найти предел последовательности
Это пример для самостоятельного решения. Здесь аргумент арктангенса также бесконечно мал, поскольку его знаменатель более высокого порядка роста, чем числитель. Решать, разумеется, значительно выгоднее через замечательную эквивалентность.
Оба рассмотренных примера справедливы и для функций, похожие пределы также разобраны в Примерах 12-13 урока о бесконечно малых величинах.
В заключение урока рассмотрим ещё один важный вопрос:
Как найти предел знакочередующейся последовательности?
Такая последовательность уже неоднократно встречалась в статье, например, первая скрипка теоретического параграфа 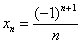
Действительно, как аналитически найти предел знакочередующейся последовательности, если знак то «плюс», то «минус»?
И я, наконец-то, заряжаю в свой револьвер тот самый волшебный патрон:
Найти предел последовательности
Решение: на первом шаге следует найти предел последовательности 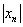
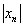
Теперь как ни в чём не бывало, вымучиваем наш обычный предел:
Получено конечное число. Очевидно, что знакочередование не поменяет сути – члены последовательности будут «прыгать» вокруг своего предела, бесконечно близко приближаясь к нему. Собственно, это проиллюстрировано на единственном рисунке данного урока.
Ситуация принципиально такая же, как, например, у более простых последовательностей 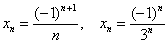
Ответ: так как последовательность является знакочередующейся и 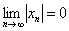
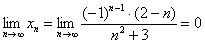
Если в ходе исследования знакочередующейся последовательности 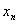
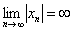
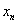
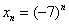
Наше увлекательное путешествие в мир последовательностей подошло к концу и, надеюсь, оно составило достойную конкуренцию Вконтакте =) =) =)
Пример 2: Решение: 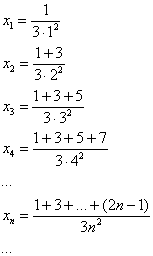
Найдём предел последовательности: 
Используем формулу суммы 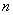
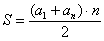
В данном случае 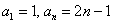
Пример 4: Решение:
Пример 6: Решение:
Пример 8: Решение:
Пример 10: Решение: последовательность 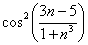
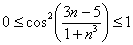
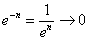
Пример 12: Решение: 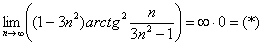
Заменим бесконечно малую эквивалентной: 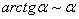
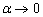
В данном примере 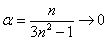
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5