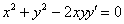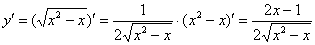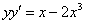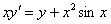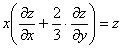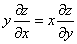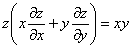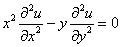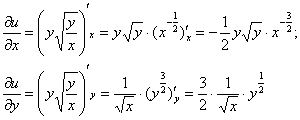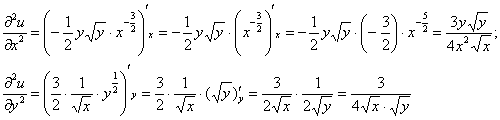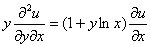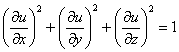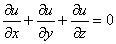Доказать что функция удовлетворяет уравнению

Как проверить, удовлетворяет ли функция уравнению?

На дворе начало апреля 2015 и эти солнечные, но ещё холодные деньки навеяли ностальгические воспоминания о своих первых, во многом любительских заметках по высшей математике. Но время шло, тараканы взрослели, и мой стиль становился всё более и более академичным, а статьи – всё более объёмными и обстоятельными. Однако, не зря говорят, что всё возвращается на круги своя, и, видимо, поэтому сегодня появилось желание вернуться к той же лёгкости и непринуждённости изложения материала. По крайне мере, я попытаюсь =)

Задание, сформулированное в заголовке статьи, оказалось обойдено вниманием в теме «обычных» производных (производных функции 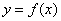), и, прежде чем перейти к примерам с функциями нескольких переменных, наверстаем упущенное:

Проверить, удовлетворяет ли функция 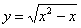уравнению

! Примечание: в условии таких задач производную нередко обозначают через 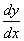, и это не должно сбивать с толку!

Решение: поскольку в предложенное уравнение входит не только функция, но и её производная, то сначала следует найти производную:

Далее решение можно оформить двумя эквивалентными способами:

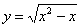
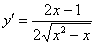
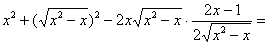
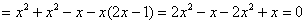
Стиль №1. Подставим и в левую часть уравнения и проведём упрощения:

– в результате получена правая часть, таким образом, данная функция удовлетворяет данному уравнению.

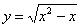
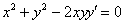
Что это, кстати, значит? Грубо говоря, функция является корнем уравнения .

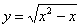
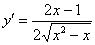
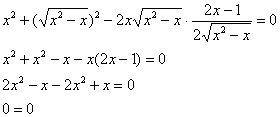
Стиль №2. Подставим и в уравнение и выполним упрощения (в данном случае только левой части):

Получено верное равенство.

Ответ: данная функция удовлетворяет данному уравнению.

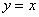
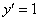
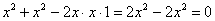
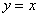
Аналогичную проверку, разумеется, можно выполнить и для других функций. Так, например, подставим и её производную в левую часть уравнения (Стиль №1):
– получена правая часть, значит, функция тоже удовлетворяет данному уравнению.

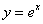
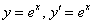
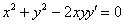
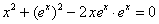
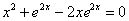
А вот, скажем, функция «не подходит». И действительно, подставляя в уравнение (Стиль №2):

– получаем неверное равенство.

Совершенно понятно, что таких «неудовлетворительных» функций – великое множество.

Многие читатели уже давно интуитивно чувствуют нечто знакомое, и это неспроста! Всем с раннего детства знакома ситуация, когда, широко разинув рот, с интересом слушаешь взрослого, после чего там оказывается невкусная таблетка…, а то и вообще шприц в попе =) Вот и сейчас вы побывали в похожей ситуации! – неожиданно так, чтобы испугаться никто не успел, познакомил я вас с одной ужасной вещью:))

– это не что иное, как дифференциальное уравнение, а функция – одно из его решений. Дифференциальные уравнения мы научимся решать позже, а пока что проведём «артподготовку» к этой теме. Самостоятельно:

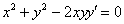
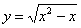
Проверить, удовлетворяет ли функция 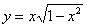уравнению

Здесь решение чуть выгоднее провести первым способом, т.е. найти производную и подставить 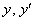в левую часть уравнения с дальнейшими преобразованиями.

Проверить, удовлетворяет ли функция 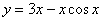уравнению

В этом же задании подстановка осуществляется в обе части уравнения и по этой причине удобнее использовать 2-й способ, получив верное либо неверное равенство.

Следует отметить, что функция вовсе не обязана удовлетворять уравнению, и иногда приходится давать противоположный ответ: «данная функция НЕ удовлетворяет данному уравнению». Но такой исход всегда неприятен, поскольку начинает мерещиться, что где-то допущена ошибка, после чего следует тщательная проверка, а зачастую и параноидальная перепроверка решения.

Примерные образцы чистового оформления примеров внизу страницы.

Как я уже намекнул в самом начале, рассматриваемое задание значительно чаще формулируется для функции нескольких, а точнее – для функции двух переменных; поэтому данный урок и оказался в разделе ФНП. Предполагается, что на данный момент вы умеете находить частные производные функции двух переменных:

Проверить, удовлетворяет ли функция 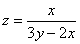уравнению

И сразу обращаю внимание на запись частных производных – в подавляющем большинстве подобных примеров вы встретите именно громоздкие обозначения. В принципе, уравнение можно переписать в виде 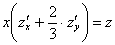и это ни в коем случае не будет ошибкой, но я буду придерживаться традиционного стиля, с которым вы вероятнее всего столкнётесь на практике.

Решение: в предложенное уравнение входит как сама функция, так и её частные производные первого порядка, что сподвигает к естественным действиям: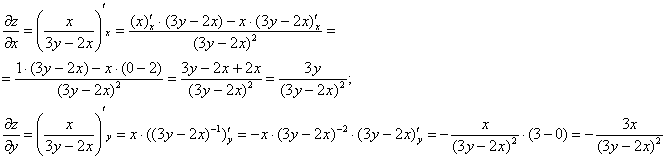

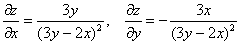
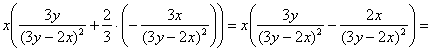
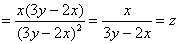
Решение, напоминаю, можно оформить двумя способами, и, на мой взгляд, здесь проще подставить найденные частные производные в левую часть:

– «на выходе» получена правая часть нашего уравнения.

Ответ: данная функция удовлетворяет данному уравнению.

Пара примеров для самостоятельного решения:

Проверить, удовлетворяет ли функция 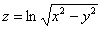уравнению

Тут сподручнее выполнить подстановку в обе части и получить верное или неверное равенство.

То же задание для функции 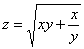и уравнения

А здесь удобнее упростить левую часть и выяснить, получится ли в итоге .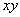

Предостерегаю от мысли «Да чего тут решать, и так всё понятно». Добросовестно прорешивая примеры, вы не только отрабатываете тематическую задачу, но и шлифуете свою технику нахождения частных производных. И это тем более важно, поскольку я предлагаю вам не абы какие-то задачки, а связный, методически продуманный курс статей – чтобы полученные знания и навыки остались с вами надолго. Таким образом, наш урок вовсе не закончился – он в самом разгаре!

Решения и ответы в подвале.

Помимо частных производных 1-го порядка, в уравнении могут присутствовать и частные производные более высоких порядков, как правило – второго:

Проверить, удовлетворяет ли функция 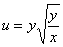уравнению

Здесь вместо буквы «зет» использована буква «у», что является весьма распространённым вариантом обозначения функции.

Решение: сначала найдём частные производные 1-го порядка:

Затем входящие в уравнение частные производные 2-го порядка:

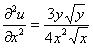
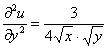
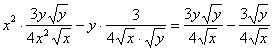
Подставим и в левую часть уравнения:
– в результате НЕ получена правая часть данного уравнения.

Ответ: данная функция не удовлетворяет данному уравнению.

Так действительно бывает!

Интересное задание для самостоятельного решения:

Проверить, удовлетворяет ли функция 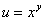уравнению

Краткое решение и ответ в конце урока.

И заключительные примеры посвящены тому же заданию, но с функцией 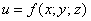трёх переменных. Следует отметить, что в «реальном» практическом примере вам вряд ли напишут, скольких переменных дана функция, и этот момент всегда следует прояснять самостоятельно:

Проверить, удовлетворяет ли функция 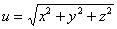уравнению

Решение: найдём частные производные 1-го порядка функции трёх переменных: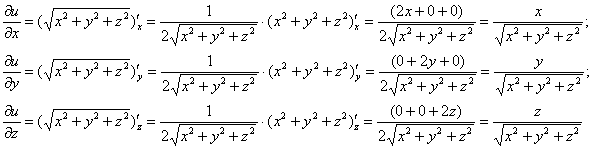

Симметрия это не только красиво – но ещё и очень удобно!

Теперь важно не перепутать квадраты производных с производными второго порядка. Подставим найденные производные в левую часть уравнения:

– получена правая часть данного уравнения.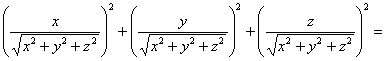

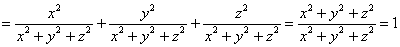
Ответ: дфуду

Вот так и рождаются новые ругательства =)

Симметрия по вашу душу:

Проверить, удовлетворяет ли функция 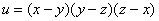уравнению

Подумайте, как рациональнее оформить решение.

Дополнительные задания по теме можно найти в задачнике Рябушко (ИДЗ 10.2), ну а я в лучших традициях своего «раннего творчества» отпускаю вас пораньше =) Сейчас ещё раз перечитаю текст и постараюсь избавить его от излишней наукообразной лексики…, хотя наставление в середине статьи всё-таки оставлю, что делать – старею =)

Надеюсь, мои уроки удовлетворяют вашим ожиданиям, и после перемены я жду вас на странице Частные производные неявно заданной функции.

Пример 2: Решение: найдём производную: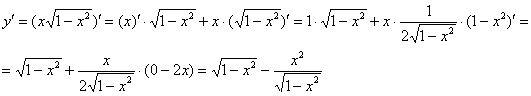

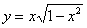
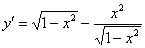
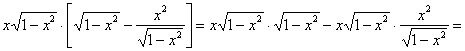
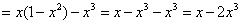
Подставим и в левую часть уравнения:

– в результате получена правая часть данного уравнения.
Ответ: данная функция удовлетворяет данному уравнению.

Пример 3: Решение: найдём производную: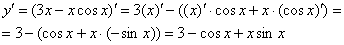

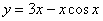
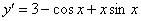
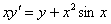
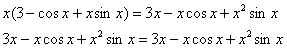
Подставим и в уравнение :

Получено верное равенство.
Ответ: данная функция удовлетворяет данному уравнению.

Пример 5: Решение: используя свойства логарифмов, преобразуем функцию: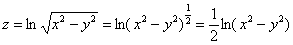

Найдём частные производные первого порядка: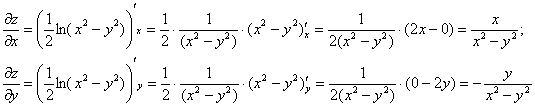

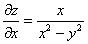
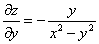
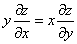
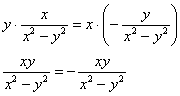
Подставим и в уравнение :

Получено неверное равенство.
Ответ: данная функция не удовлетворяет данному уравнению.

Пример 6: Решение: найдём частные производные первого порядка: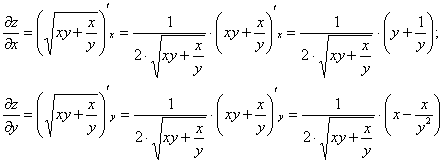

Подставим функцию и найденные производные в левую часть уравнения:

– получена правая часть данного уравнения.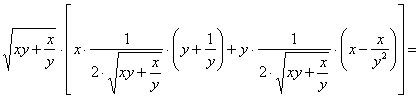
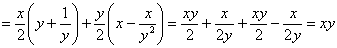
Ответ: данная функция удовлетворяет данному уравнению.

Пример 8: Решение: найдём частную производную по «икс»:
(т.к. константой считается «игрек», то производная берётся от степенной функции)
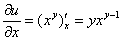
Найдём смешанную частную производную 2-го порядка:

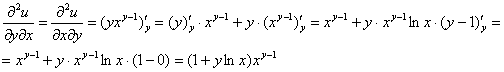
(т.к. константой считается «икс», то производная 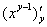берётся как производная от показательной функции)
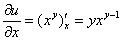
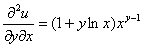
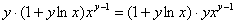
Подставим и в уравнение:

Получено верное равенство.
Ответ: данная функция удовлетворяет данному уравнению.

Пример 10: Решение: преобразуем функцию: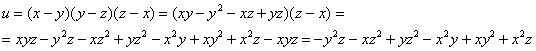

Найдем частные производные первого порядка: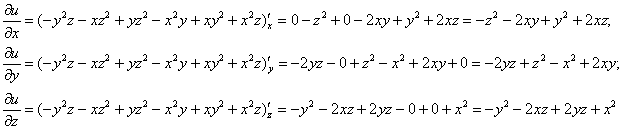

Подставим найденные производные в уравнение :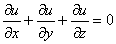

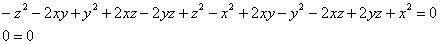
Получено верное равенство
Ответ: данная функция удовлетворяет данному уравнению.

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Источник

Функциональные уравнения. Методы их решения

Министерство образования и молодежной политики Чувашской Республики

БОУ ДПО (ПК) С «Чувашский республиканский институт образования»

Кафедра математики и информационных технологий

Курсовая работа на тему:

« Функциональные уравнения. Методы их решения»

Выполнил (а): учитель математики МБОУ «СОШ № 60»

Глава 1. Понятие функционального уравнения ………………………………. 5

Глава 2. Практическая часть. Методы решения функционального уравнения.9

Что же такое функциональные уравнения? И какие способы их решения существуют? Эти вопросы заинтересовали меня, и я решила провести исследование. функциональный уравнение коши

Функциональными уравнениями занимаются с очень давних пор, этому курсу так и не нашлось достойного места в математических программах. А жаль. Ведь решение отдельных функциональных уравнений требует достаточно глубокого понимания предмета и прививает любовь к самостоятельной творческой работе. Так как эта тема в школьном курсе не изучается в виду её сложности, при поступлении в престижные ВУЗы, на олимпиадах, в части С ЕГЭ такие задачи встречаются.

В настоящее время практически нет никаких пособий, обучающих решению функциональных уравнений.

Поэтому ощущается потребность в пособии, которое на простых и конкретных примерах способно показать читателю со скромной математической подготовкой весь арсенал современных методов решения функциональных уравнений.

1. изучение и анализ литературы;

2. поиск способов решения функциональных уравнений и их систем;

3. решение функциональных уравнений

4. составление сборника

Объект исследования: функциональные уравнения

Предмет исследования: изучение свойств и способов решения функциональных уравнений.

Структура: введение, понятие функционального уравнения, сборник задач, заключение.

Глава 1. Понятие функционального уравнения

Функциональное уравнение – это уравнение, которое содержит одну или несколько неизвестных функций (с заданными областями определения и значений). Решить функциональное уравнение – это, значит, найти все функции, которые тождественно ему удовлетворяют. Функциональные уравнения возникают в самых различных областях математики, обычно в тех случаях, когда требуется описать все функции, обладающие заданными свойствами. Термин функциональное уравнение обычно используется для уравнений, несводимых простыми способами к алгебраическим уравнениям. Эта несводимость чаще всего обусловлена тем, что аргументами неизвестной функции в уравнении являются не сами независимые переменные, а некоторые данные функции от них. Часто встречаются на различных математических соревнованиях.

Некоторые функциональные уравнения знакомы нам еще из школьного курса это

которые задают такие свойства функций, как чётность, нечётность, периодичность.

Задача решения функциональных уравнений является одной из самых старых в математическом анализе. Они появились почти одновременно с зачатками теории функций. Первый настоящий расцвет этой дисциплины связан с проблемой параллелограмма сил. Ещё в 1769 году Даламбер свёл обоснование закона сложения сил к решению функционального уравнения

(1)

То же уравнение и с той же целью было рассмотрено Пуассоном в 1804 году при некотором предположении аналитичности, между тем как в 1821 году Коши (1789 – 1857) нашёл общие решения

этого уравнения, предполагая только непрерывность f(x).

Даже известная формула неевклидовой геометрии для угла параллельности

была получена Н. И. Лобачевским (1792 – 1856) из функционального уравнения

, (2)

которое он решил методом, аналогичным методу Коши. Это уравнение можно привести к уравнению

.

Ряд геометрических задач, приводящих к функциональным уравнениям, рассматривал английский математик Ч. Баббедж (1792—1871). Он изучал, например, периодические кривые второго порядка, определяемые следующим свойством для любой пары точек кривой: если абсцисса второй точки равна ординате первой, то ордината второй точки равна абсциссе первой. Пусть такая кривая является графиком функции у = f(х) ; (х, f(х)) — произвольная ее точка. Тогда, согласно условию, точка с абсциссой f(х) имеет ординату х. Следовательно,

(3)

Функциональному уравнению (3) удовлетворяют, в частности, функции:

,

Одними из простейших функциональных уравнений являются уравнения Коши

Эти уравнения Коши подробно изучил в своём (Курсе Анализа), изданном в 1821 году. Непрерывные решения этих четырёх основных уравнений имеют соответственно вид

, , ,

В классе разрывных функций могут быть и другие решения. Уравнение (4) ранее рассматривалось Лежандром и Гауссом при выводе основной теоремы проективной геометрии и при исследовании гауссовского закона распределения вероятностей.

Источник