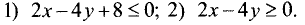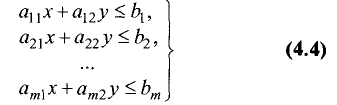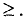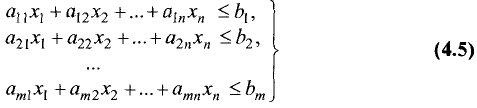Доказать что круг выпуклое множество

Доказать что круг выпуклое множество

Одним из важнейших классов тел является класс выпуклых тел. Перед тем как рассказать о нем, познакомимся с более общим понятием выпуклой фигуры.

Фигура называется выпуклой, если вместе с каждыми двумя своими точками она содержит и соединяющий их отрезок (рис. 10.6).

Точка и пустое множество (фигура, не имеющая точек) считаются выпуклыми фигурами.

Примеры выпуклых фигур: отрезок, луч, прямая, плоскость, треугольник, параллелограмм, круг, все пространство, полупространство, шар (рис. 10.7). Докажем, например, что круг — выпуклая фигура.

Рассмотрим круг D радиуса R с центром О (рис. 10.8). Возьмем любые две точки . Тогда Возьмем любую точку Z на отрезке XY. Тогда выполняется хотя бы одно из двух неравенств: или (так как хотя бы один из смежных углов OZX и OZY не острый). Поскольку то и , т. е. . А это значит, что отрезок XY содержится в круге , т.е. круг D — выпуклая фигура.

Докажем несколько предложений о выпуклых фигурах. Начнем с самого важного из них.

Предложение 1. Пересечение (общая часть) любых двух выпуклых фигур есть выпуклая фигура, и вообще, пересечение любой совокупности выпуклых фигур есть выпуклая фигура.

Пусть — две выпуклые фигуры и F — их пересечение (рис. 10.9). Если две точки принадлежат фигуре F, то значит они принадлежат и фигурам . А тогда по выпуклости фигуры она содержит отрезок АВ. Аналогично, содержит отрезок АВ. Поэтому отрезок АВ содержится и в , т. е., в фигуре F. Итак, отрезок, соединяющий любые две

точки А и В фигуры F, содержится в F, т. е., фигура F — выпуклая фигура.

В случае пересечения любой совокупности выпуклых фигур доказательство то же, но следует говорить не о двух фигурах, а сразу о фигурах всей совокупности. Повторите это доказательство еще раз.

Замечание. В частности, пересечение данных фигур может быть пустым или одноточечным множеством. Если бы пустое и одноточечное множества не считались выпуклыми, то эти случаи надо было бы исключить из теоремы и ее нельзя было бы формулировать так кратко.

Предложение 1 позволяет получать выпуклые фигуры путем пересечения каких-либо выпуклых фигур. Например, треугольник ABC можно получить пересечением трех полуплоскостей, на границах которых лежат две вершины треугольника и внутри них — третья вершина (рис. 10.10). Часто используются и следующие три утверждения.

Предложение 2. Пересечение выпуклой фигуры с плоскостью является выпуклой фигурой (рис. 10.11).

Оно вытекает из предложения 1 и выпуклости плоскости.

Предложение 3. Каждая плоскость разбивает любую выпуклую фигуру на две выпуклые фигуры (рис. 10.11). Каждая из них есть пересечение исходной выпуклой фигуры с полупространством, ограниченным данной плоскостью.

Отметим, что точки исходной фигуры, лежащие в этой плоскости, относятся к каждой из полученных выпуклых фигур.

Предложение 4. Проекция выпуклой фигуры на плоскость есть выпуклая фигура.

Действительно, пусть F — выпуклая фигура и F — ее проекция на плоскость а (рис. 10.12). Возьмем любые две точки А и В фигуры F. Они являются проекциями некоторых точек А и В фигуры F. Поскольку F — выпуклая фигура, то отрезок АВ содержится в фигуре F. Значит проекция отрезка АВ — отрезок АВ — содержится в фигуре F, т. e., F— выпуклая фигура.

Отметим также, что цилиндр и конус выпуклы тогда и только тогда, когда их основания — выпуклы. Докажем это, например, для цилиндра.

Следует доказать два утверждения:

1) если цилиндр выпуклый, то его основание — выпукло;

2) если основание цилиндра выпукло, то и сам цилиндр выпуклый.

Первое утверждение непосредственно вытекает из предложения 2, так как основание цилиндра является пересечением цилиндра с плоскостью этого основания.

Докажем второе утверждение. Пусть основание F цилиндра С выпукло (рис. 10.13). Возьмем в цилиндре любые две точки А и В и проведем через них образующие и . Если А и В лежат на одной образующей, то отрезок А В лежит в цилиндре С. Поэтому будем считать, что образующие различны. Концы этих образующих, лежащие в F, — точки X и Y — являются концами отрезка XY, лежащего в F, так как основание F — выпукло.

Поэтому все отрезки , исходящие из точек Z отрезка XY, параллельные и равные отрезку , являются образующими цилиндра С. Следовательно, параллелограмм содержится в цилиндре С.

Так как отрезок АВ содержится в параллелограмме XXY Y, то отрезок А В содержится в С. Итак, цилиндр С выпуклый.

Источник

Задача Докажите, что: а круг выпуклое множество

Множество называется выпуклым, если вместе с любыми двумя своими точками целиком содержит отрезок, их соединяющий.

Пример 1. На числовой прямой выпуклые множества – это промежутки, и только они.

Пример 2. Выпуклость многоугольника означает, что он лежит по одну сторону от каждой своей стороны
Задача 1. Докажите, что:

б) множество точек, лежащих выше параболы выпукло;

в) пересечение выпуклых множеств выпукло;

г) выпуклость четырехугольника означает, что его диагонали пересекаются.
Задача 2.

а) На прямой есть три отрезка, любые два из которых пересекаются. Докажите, есть точка, принадлежащая всем трем отрезкам.

б) Докажите, что в а) вместо можно поставить любое .

в) На прямой есть выпуклых множеств, любые два из которых пересекаются. Докажите, есть точка, принадлежащая всем множествам.

г) Верно ли в) для бесконечного числа выпуклых множеств?
Задача 3.

а) На плоскости есть прямоугольников со сторонами, параллельными осям координат. Известно, что любые два прямоугольника пересекаются. Докажите, есть точка, принадлежащая всем прямоугольникам.

б) Отрезок покрыт конечным числом меньших отрезков. Докажите, что левые половины этих отрезков покрывают не менее половины длины всего отрезка.

в) Отрезок покрыт конечным числом меньших отрезков. Докажите, что несколько непересекающихся отрезков по длине не меньше половины всего отрезка.

г) Квадрат разрезан на несколько прямоугольников. Докажите, что можно закрасить несколько из них так, чтобы их проекция на одну сторону квадрата имела длину не меньше , а проекция на другую сторону квадрата имела длину не больше .
Задача 4.

а) На плоскости есть 5 точек (никакие 3 не лежат на одной прямой). Докажите, что какие-то 4 лежат в вершинах выпуклого четырехугольника.

б) На плоскости есть 5 точек, любые 4 из которых лежат в вершинах выпуклого четырехугольника. Докажите, что это – вершины выпуклого пятиугольника.

в) Докажите б) для точек.

г) На плоскости задано 6 точек (никакие 3 не лежат на одной прямой). Докажите, что из них можно выбрать 3 так, чтобы один из углов треугольника с вершинами в этих точках был не меньше 120;
Задача 5. (Теорема Хелли)

а) На плоскости даны четыре выпуклые фигуры, каждые три из которых имеют общую точку. Докажите, что все эти фигуры имеют общую точку. б) То же для выпуклых фигур.

в) Привести пример, показывающий, что а) неверно в случае невыпуклых фигур.

г) Привести пример, показывающий, что б) неверно для бесконечного числа замкнутых полуплоскостей.

ПРИМЕНЕНИЯ ТЕОРЕМЫ ХЕЛЛИ.

а) Докажите, что внутри выпуклого семиугольника есть точка, не принадлежащая ни одному из четырехугольников, образованных четверками его соседних вершин.

б) Плоскость освещена несколькими прожекторами, каждый из которых освещает некоторую полуплоскость. Докажите, что для освещения всей плоскости достаточно некоторых трех прожекторов.

г) Любые две фигуры из плоских выпуклых фигур имеют общую точку. Тогда через любую точку плоскости можно провести прямую, пересекающую все фигуры.

д) Комната имеет форму невыпуклого многоугольника. Известно, что любые три стены комнаты можно осветить, подходящим образом располагая люстру внутри комнаты. Докажите, что все стены можно осветить из некоторой точки комнаты.

е) Про n вертикальных отрезков известно, что любые три из них можно перечеркнуть какой-нибудь наклонной прямой. Докажите, что и все отрезки сразу можно перечеркнуть какой-нибудь наклонной прямой. (Отрезки можно заменить выпуклыми фигурами).
Задача 7 (Что-то вроде описанной окружности)

а) Стороны треугольника не больше . Докажите, что радиус описанной окружности не больше .

б) Есть кругов радиуса , любые 3 из которых пересекаются. Докажите, что все эти круги можно накрыть одним кругом радиуса 2r.

в) Попарные расстояния между точками на плоскости не больше единицы. Докажите, что все эти точки помещаются в некотором круге радиуса (теорема Юнга).

г) Если диаметр плоской фигуры меньше , то вся фигура лежит в некотором круге радиуса .
Задача 8 (Что-то вроде центра)

а) Для любых 7 точек на плоскости можно найти точку О такую, что по обе стороны от любой прямой, проходящей через О лежит не менее трех из этих точек. (Прямая включается в полуплоскость.)

в) Привести пример, показывающий неулучшаемость оценки 1/3 в б).

г) Пусть О – центр тяжести треугольника и АВ – «хорда» проходящая через О. Тогда и АО и ВО не меньше трети АВ.

д) Внутри любого многоугольника есть точка О такая, что отрезки любой хорды, проходящей через нее, не меньше трети хорды. (Указание: для каждой граничной точки рассмотреть (2/3)-гомотетичные образы фигуры.)

е) Внутри треугольника нет точки О такой, что отрезки любой хорды, проходящей через нее, больше трети хорды. Значит, оценка 1/3 в д) неулучшаема.
Задача 9. (Что-то вроде комбинаторики)

а) На круглом столе радиуса расположено без наложений монет радиуса так, что больше ни одной монеты положить нельзя. Доказать, что .

б) В прямоугольнике 20 25 расположено 120 единичных квадратов. Докажите, что в него поместится не задевающий их круг единичного диаметра.

в) В круге радиуса 16 расположены 650 точек. Докажите, что есть круговое кольцо с внутренним радиусом 2 и внешним радиусом 3, в котором лежит не менее 10 из этих точек.

г) Докажите, что в выпуклый многоугольник площади S и периметра P можно вписать круг радиуса S/P.

Источник

Выпуклые множества точек и их свойства с примерами решения и образцами выполнения

Основные определения:

Множество точек называется выпуклым, если оно вместе с любыми
двумя своими точками содержит весь отрезок, соединяющий эти точки.

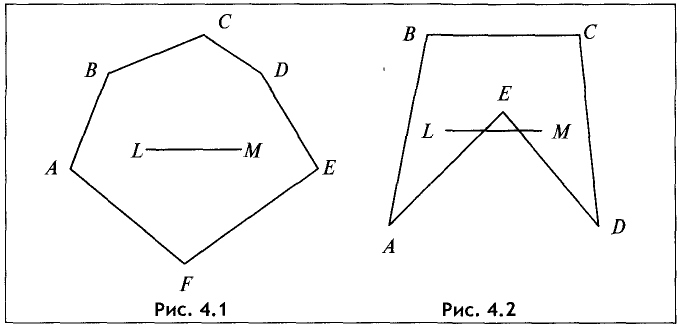
Например, многоугольник, представленный на рис. 4.1,
является выпуклым, а многоугольник на рис.4.2 выпуклым не является.

Выпуклыми множествами могут быть не только многоугольники. Примерами выпуклых множеств являются прямая, круг, куб,
многогранная область, полуплоскость, полупространство и т.д.

Пересечение любого числа выпуклых множеств есть выпуклое
множество.

Точка множества называется внутренней, если в любой ее окрестности (например, круг или шар с центром в этой точке) содержатся точки только данного множества.

Точка множества называется граничной, если в любой ее окрестности содержатся как точки, принадлежащие данному множеству, так и точки, не принадлежащие ему.

Точка множества называется угловой (крайней), если она не является внутренней ни для какого отрезка, целиком принадлежащего данному множеству.

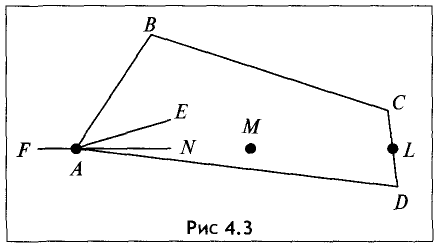
Примеры угловой А, внутренней L и граничной М точек приведены на рис. 4.3.

Точка А является угловой, так как для любого отрезка АЕ,
целиком принадлежащего многоугольнику, она не является
внутренней. Точка А — внутренняя для отрезка FN, но этот отрезок не принадлежит целиком множеству.

Для выпуклого множества угловые точки всегда совпадают с вершинами многоугольника (многогранника).

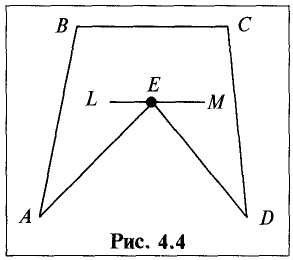
Так, на рис. 4.4 точка Е является вершиной невыпуклого многоугольника, но не является угловой, так как она является внутренней для отрезка LM, целиком принадлежащего этому
многоугольнику.

Множество точек называется замкнутым, если оно включает все свои граничные точки.

Множество точек называется ограниченным, если существует круг (шар) радиуса конечной длины с центром в любой точке множества, который полностью содержит в себе данное множество. В противном случае множество называется неограниченным.

Выпуклое замкнутое множество точек плоскости (пространства), имеющее конечное число угловых точек, называется выпуклым многоугольником (многогранником), если оно ограниченное, и выпуклой многоугольной (многогранной) областью, если оно неограниченное.

Введенные понятия рассматривались для множества точек на
плоскости и в пространстве. Их можно обобщить также на n-мерное
точечное пространство.

Геометрический смысл решений неравенств

Рассмотрим решения неравенств с двумя переменными типа

Теорема:

Множество решений неравенств с двумя переменными (4.1) является одной из двух полуплоскостей, на которые вся плоскость делится прямой

включая и эту прямую, а другая полуплоскость — множеством решений неравенства

Пример:

Построить график множества решений следующих
неравенств:

Решение:

В соответствии с теоремой множество решений
приведенных неравенств есть полуплоскость.

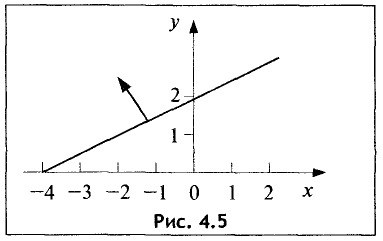
1.Границей первой полуплоскости является прямая

Представим уравнение этой прямой в виде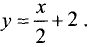
Ее график представлен на рис. 4.5.

Для определения искомой полуплоскости зададим произвольную контрольную точку, не лежащую на построенной прямой. Проще всего задать точку с координатами (0; 0). Подставив данные
координаты в неравенство

видим, что оно не выполняется, так как 8 > 0. Поэтому искомой является верхняя полуплоскость.

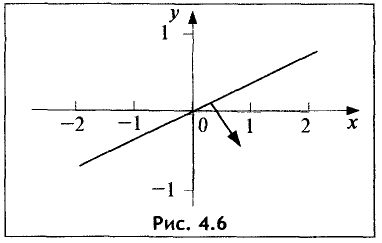
2.Границей второй полуплоскости является прямая

Представим это уравнение в виде

График исследуемой прямой представлен на рис. 4.6.

В данном случае точка с координатами (0; 0) лежит на этой
прямой. Поэтому выбираем точку с координатами (0; —1) и подставляем данные координаты в неравенство 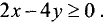Так как неравенство выполняется (4 > 0), то искомой является нижняя полуплоскость. ►

Основные свойства выпуклого множества точек

Рассмотрим множество решений совместной системы линейных
неравенств с двумя переменными.

Теорема:

Множество решений совместной системы т линейных
неравенств с двумя переменными

является выпуклым многоугольником (или выпуклой многоугольной областью).

Знаки некоторых или всех неравенств могут быть

Эту теорему для n переменных можно сформулировать
следующим образом.

Теорема:

Множество решений совместной системы m линейных
неравенств с n переменными

является выпуклым многогранником (или выпуклой многогранной областью) в n-мерном пространстве.

Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью решения системы.

Область решений системы, удовлетворяющая условиям неотрицательности 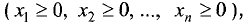называется областью неотрицательных (или допустимых) решений.

Пример:

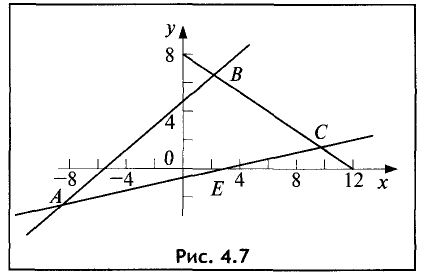
Построить область решений и область допустимых
решений системы неравенств и определить координаты угловых точек области допустимых решений:

Решение:

Областью решений является треугольник ABC, представленный на рис. 4.7.

Для нахождения искомой полуплоскости зададим контрольную
точку с координатами (0; 0). Подставив данные координаты в неравенство 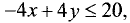видим, что оно выполняется, так как 0

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Теорема 3

Свойства выпуклого множества

1. Теорема 1

Пересечение выпуклых множеств является выпуклым множеством.

Докажем, что Х выпуклое множество.

Пусть точки и Х. Докажем, что отрезок, соединяющий эти точки, тоже принадлежит множеству Х.

Х2 выпуклое множество.

2. Теорема 2.

Объединение выпуклых множеств не всегда является выпуклым.

3. Свойство определённости.

+ = с такая, что будут выполняться неравенства

Гиперплоскостью в пространстве R называется множество точек x ( которая удовлетворяет равенству

Пусть Х это замкнутое выпуклое множество. Точка не принадлежит множеству Х. Тогда существует гиперплоскость с нормальным так, что для любой точки будут выполняться неравенства.

Определение 1. Выпуклое замкнутое множество точек пространство имеющие конечное число угловых точек, называется выпуклым многогранником. Если оно ограничено и выпуклой многогранной областью если оно не ограничено (нет точек бесконечности).

Определение 2. Точка называется внутренней если существует окружность, в которой содержатся только из рассматриваемого множества.

Определение 3. Точка называется граничной точкой множества если в любой её окрестности содержатся точки, которые как принадлежат этому множеству, так и не принадлежат ему.

Определение 4. Точка множества называется угловой (крайней) если она не является внутренней ни для одного отрезка целиком принадлежащему этому множеству.

Рассмотрим систему линейных неравенств.

1, 2, 3 – это тождественные формы записи системы неравенств.

Теорема:

Пусть Х множество допустимых векторов система тогда это множество выпукло и замкнуто.

I. Докажем, что полупространство удовлетворяющее неравенству

, i является выпуклым.

II. Так как вектора удовлетворяющие одновременно всем неравенствам системы образуют множество, которое является пересечением множеств для каждого неравенства, то по теореме (1) это множество выпукло.

III. Замкнутость данного множества вытекает из непрерывности рассматриваемых линейных функций.

Используя это определение можно переформулировать определение выпуклого множества следующим образом:

Множество называется выпуклым, если оно содержит выпуклую линейную комбинацию для любых двух своих точек.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник