Доказать что многочлен делится на число

Делимость многочленов. Свойства делимости

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

НАБЕРЕЖНОЧЕЛНИНСКИЙ ГОСУДАРСТВЕННЫЙ

ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ

МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ

КАФЕДРА МАТЕМАТИКИ И МЕТОДИКИ ЕЕ ПРЕПОДАВАНИЯ

АЛГОРИТМЫ С МГНОГОЧЛЕНАМИ

/дипломная работа/

Набережные Челны

Содержание

2. Деление многочленов

2.1. Делимость многочленов. Свойства делимости

2.2. Деление многочленов с остатком

2.3. Наибольший общий делитель многочленов

2.4. Алгоритм Евклида

4. Производная от многочлена

5. Кратные множители

5.1. Выделение кратных множителей

Список использованной литературы

Введение

Тема моей дипломной работы: «Алгоритмы с многочленами».

Целью данной работы является изучение многочленов, алгоритмов с ними, рассмотрение возможностей составления различных программ. Для достижения поставленной цели необходимо рассмотреть следующие вопросы:

– деление многочленов с остатком;

– наибольший общий делитель, алгоритм Евклида;

– кратные множители, выделение кратных множителей;

– производные от многочленов.

Для выполнения дипломной работы я поставила следующие задачи:

1. изучить литературу о многочленах;

2. применить теорию высшей алгебры в решении задач элементарной математики;

3. составить программы для нахождения частного и остатка при делении многочленов, наибольшего общего делителя двух многочленов, производной многочлена; разложения многочленов на кратные множители.

Многочлены

Общий вид уравнения n-ной степени (где n некоторое положительное число) есть

. (1.1)

Коэффициенты этого уравнения мы будем считать произвольными комплексными числами, причем старший коэффициент должен быть отличным от нуля.

Если написано уравнение (1.1), то всегда предполагается, что требуется его решить, найти такие числовые значения для неизвестного x, которые удовлетворяют этому уравнению, то есть после подстановки вместо неизвестного и выполнения всех указанных операций обращают левую часть уравнения (1.1) в нуль.

Целесообразно заменить задачу решения уравнения (1.1) более общей задачей изучения левой части этого уравнения

, (1.2)

Деление многочленов

Теория многочленов в определенном отношении похожа на теорию целых чисел, хотя внешне эти две теории не имеют ничего общего. Внутренняя же близость, схожесть этих теорий объясняется тем, что для многочленов, так же как и для целых чисел, можно определить деление и, что еще более важно, деление с остатком.

Делимость многочленов. Свойства делимости

Многочлен делится на многочлен , если существует такой многочлен , что выполняется равенство

(2.1)

Например, из равенства следует, что делится на многочлен и на многочлен .

Многочлен в равенстве (2.1) определяется однозначно. Если бы существовал многочлен , удовлетворяющий равенству (2.1), то мы получили бы, что

(2.2)

откуда

Но многочлен по условию ненулевой, и в силу утверждения или нулевом является многочлен , т.е. многочлен совпадает с .

Многочлен в равенстве (2.1) называется частным от деления на , а – делителем.

Укажем некоторые основные свойства делимости многочленов.

1. Если делится , а делится на , то будет делиться на .

В самом деле, по условию и , а поэтому .

2. Если и делятся на , то их сумма и разность также делятся на .

Из равенств и вытекает .

3.Если делится на , то произведение на любой многочлен также будет делиться на .

Если , то .

Из 2. и 3. вытекает следующее свойство:

4. Если каждый из многочленов 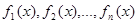делится на , то на будет делиться и многочлен , где — произвольные многочлены.

5. Всякий многочлен делится на любой многочлен нулевой степени.

6. Если делится на , то делится и на с , где с – произвольное число отличное от нуля.

Из равенства следует равенство .

7. Многочлены 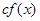, , и только они будут делителями многочлена , имеющими такую же степень, что и .

Действительно, . То есть делится на .

Если делится на , причем степени и совпадают, то степень частного от деления на должна быть равной нулю, то есть , , откуда .

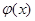
Отсюда вытекает следующее свойство:

8. Тогда и только тогда многочлены , одновременно делятся друг на друга, если , .

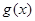
Из 1. и 8. вытекает свойство:

9. Всякий делитель одного из двух многочленов , , где , будет делителем и для другого многочлена.

Свойства делимости многочленов могут быть применены для изучения делимости в множестве целых чисел. Выясним, например, для каких целых чисел n число является простым.

Натуральное число, отличное от 1, называется простым, если оно делится только на 1 и на само себя; целое отрицательное число k называется простым, если число –k простое.

Для ответа на поставленный вопрос заметим, что справедливо равенство

(2.3)

и поэтому число делится на и на Следовательно, оно может быть простым только в случае, когда один из этих делителей равен 1 или –1, т.е. выполняется хотя бы одно из равенств

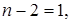
Может возникнуть вопрос: откуда взялось равенство (2.3)? Как мы догадались, что многочлен таким образом раскладывается на множители? Для нахождения разложений такого типа необязательно прибегать к искусственным группировкам, это можно сделать с помощью теории, которая будет изложена ниже.

Из этого примера видно, что уже для решения задач, связанных с делимостью целых чисел, полезно уметь выяснять, делится ли данный многочлен на некоторый другой многочлен (раскладывается ли на множители).Ответ на такой и многие другие вопросы можно найти с помощью деления многочлена с остатком.

Источник

Лекция по теме»Делимость многочленов»

Муниципальное бюджетное общеобразовательное учреждение

Средняя общеобразовательная школа п. Надвоицы

Тема: ДЕЛИМОСТЬ МНОГОЧЛЕНОВ

Забровская Алина, Зотикова Елена, Степанович Арина, обучающиеся 8 «а» класса МБОУ СОШ п. Надвоицы

Руководитель: Шалагинова Людмила Сергеевна, учитель математики

Действия с многочленами

2.1 Сложение (вычитание) многочленов

2.2 Умножение многочленов

3.1 Свойства теории делимости многочленов

3.2 Деление многочленов столбиком

Применение теории делимости

4.2 Разложение на множители

4.3 Сокращение дробей

4.4 Решение уравнений

Применение схемы Горнера при решении уравнений с параметром

Список используемой литературы и ссылки

В работе рассматриваются основы теории делимости многочленов и её применение. Кратко рассказывается об истории возникновения теории делимости. В работе представлены формулировки и основные понятия теории делимости многочленов. Показан основой принцип деления и его приложения.

Эта тема выбрана, потому что на уроках алгебры мы изучали сложение, вычитание, умножение многочленов, а вот деление многочленов нет.

Цель нашей работы : изучить теорию делимости многочленов и области ее применения.

Для достижения этой цели мы изучили основные понятия, теоремы и алгоритмы теории делимости. С помощью основ теории делимости многочленов можно делить многочлены, раскладывать многочлены на множители, решать уравнения, сокращать дроби, решать математические задачи.

Изучить основные понятия, теоремы и алгоритмы теории делимости.

Показать использование теории делимости многочленов в решении алгебраических задач.

Создать обучающие видеоуроки для учащихся по данной теме проекта.

Подобрать задачи для самостоятельного решения для учащихся 8-11 классов на применение теории делимости многочленов.

Применение теории делимости многочленов является важной частью работы: теорема Безу и её следствие, разложение многочленов на множители, сокращение дробей, решение уравнений. Поэтому в работе есть задачи на применение теории делимости многочленов и задания для самостоятельного решения.

Методами исследования являлись: анализ учебной и дополнительной литературы, собственный анализ.

В нашей работе представлены обучающие видеоуроки, где рассматриваются основы теории делимости многочленов. Они позволят разобраться ученикам в задачах, которые сложно решить, не зная данной теории. Также в работе представлен наш отчёт о проведённых уроках в некоторых классах нашей школы.

*Данный многочлен можно привести к стандартному виду. Говорят, что многочлен имеет стандартный вид, если все его члены записаны в стандартном виде и среди них нет подобных: 17aуу– 7ay 2 +5aуу+a =17ay 2 – 7ay 2 +5ay 2 +а=15ay 2 +а

Многочлены, которые состоят из двух и трех членов, имеют специальные названия – двучлен и трехчлен соответственно. Так х+у – это двучлен, а 2x 3 q−qx 2 +7b – трехчлен.

В своей работе мы будем использовать многочлены стандартного вида первой степени, второй, третьей и четвёртой. (Степенью многочлена называют наибольшую из степеней входящих в него одночленов).

2. Действия с многочленами

2.1 Сложение (вычитание) многочленов

Суммой (разностью) двух многочленов называется многочлен, коэффициенты которого являются суммой (разностью) коэффициентов при подобных членах этих многочленов.

На практике для нахождения суммы и разности многочленов используют правила раскрытия скобок, перед которыми стоит знак плюс (знак минус).

2.2 Умножение многочленов

Чтобы умножить многочлен на одночлен, нужно умножить каждый член многочлена на этот одночлен и сложить полученные произведения.

Чтобы умножить многочлен на многочлен, нужно умножить каждый член первого многочлена на каждый член второго многочлена полученные одночлены сложить.

3. Делимость многочленов

3.1 Свойства теории делимости многочленов

Теория делимости многочленов имеет следующие свойства:

1) Если P ₁ (x) и P ₂ (x) делятся на Q(x); то P ₁ (x) + P ₂ (x) и P ₁ (x) _ P ₂ (x)делятся на Q(x);

3) Если P(x) делится на Q(x), а Q(x) делится на H(x), то P(x) делится на H(x).

4) Если ненулевой многочлен P(x) делится на Q(x), то deg P(x) ≥ deg Q(x),где deg(Р(x) и Q(x)-степени этих многочленов.

5) Еесли deg P(x) = deg Q(x); то P(x) делится на Q(x) тогда и только тогда, когда эти многочлены пропорциональны (многочлены называются пропорциональными, если один из них получается из другого умножением на число, отличное от 0).

3.2 Деление многочленов столбиком

В алгебре, деление многочленов столбиком — алгоритм деления многочлена f(x) на многочлен g(x), степень которого меньше или равна степени многочлена f(x). Алгоритм представляет собой обобщенную форму деления чисел столбиком, легко реализуемую вручную.

Целью алгоритма деления многочленов в столбик является нахождение частного q(x) и остатка r(x) для заданных делимого f(x) и ненулевого делителя g(x).

Пример: Покажем, что

Частное и остаток от деления могут быть найдены в ходе выполнения следующих шагов:

в). Вычитаем полученный после умножения многочлен из делимого, записываем результат под чертой

г). Повторяем предыдущие 3 шага, используя в качестве делимого многочлен, записанный под чертой.

Первую лекцию о делимости многочленов мы провели в своём 8-а классе. На диаграмме показаны результаты самостоятельной работы «Деление многочлена на двучлен». Из 22 учеников полностью справилось 50% учеников.

Одно из заданий работы

С лекцией о делимости многочленов мы выходили в 8-в, 9-а и 10-б классы. После лекции мы проводили небольшие самостоятельные работы. Результаты работ можно увидеть на диаграммах.

Одно из заданий работы

Одно из заданий работы

Предлагаем задачи для самостоятельного решения:

1.Выполните деление с остатком многочлена 2 x 2 − 9x − 3 на х-2

Основные труды относятся к решению алгебраических уравнений. В 1819 году опубликовал способ приближённого вычисления действительных корней многочлена, который называется теперь способом Руффини-Горнера (этот способ был известен китайцам еще в XIII веке). Работа была напечатана в философских работах Королевского научного сообщества.

Схема Горнера – способ деления многочлена Р(х) на бином x−a. Работать придётся с таблицей, первая строка которой содержит коэффициенты заданного многочлена. Первым элементом второй строки будет число a, взятое из бинома x−a.

Покажем схему Горнера для многочлена четвёртой степени (частный случай).

Непосредственное применение схемы Горнера проще всего показать на примерах.

Пример №1: Разделить 5x 4 +5x 3 +x 2 −11 на x−1,используя схему Горнера.

Начнем заполнять пустые ячейки во второй строке. Во вторую ячейку второй строки запишем число 5, просто перенеся его из соответствующей ячейки первой строки:

Следующую ячейку заполним по такому принципу: 1⋅5+5=10:

Аналогично заполним и четвертую ячейку второй строки: 1⋅10+1=11:

Для пятой ячейки получим: 1⋅11+0=11:

И, наконец, для последней, шестой ячейки, имеем: 1⋅11+(−11)=0:

Задача решена, осталось только записать ответ:

Как видите, числа, расположенные во второй строке (между единицей и нулём), есть коэффициенты многочлена, полученного после деления 5×4+5×3+x2−11 на x−1. Естественно, что так как степень исходного многочлена 5x 4 +5x 3 +x 2 −11 равнялась четырём, то степень полученного многочлена 5x 3 +10x 2 +11x+11 на единицу меньше, т.е. равна трём. Последнее число во второй строке (ноль) означает остаток от деления многочлена 5x 4 +5x 3 +x 2 −11 на x−1. В нашем случае остаток равен нулю, т.е. многочлены делятся нацело.

Пример №2 : Разделить многочлен x 4 +3x 3 +4x 2 −5x−47 на x+3 по схеме Горнера.

Решение: Сразу оговорим, что выражение x+3 нужно представить в форме x−(−3). В схеме Горнера будет участвовать именно −3. Так как степень исходного многочлена x 4 +3x 3 +4x 2 −5x−47 равна четырём, то в результате деления получим многочлен третьей степени:

Полученный результат означает, что

x 4 +3x 3 +4x 2 −5x−47 =(x+3)(x 3 +0⋅x 2 +4x−17)+4=(x+3)(x 3 +4x−17)+4

В этой ситуации остаток от деления x 4 +3x 3 +4x 2 −5x−47 на x+3 равен 4.

С лекцией о делимости многочленов по схеме Горнера мы выходили в 8-в и 11 классы. После лекции мы проводили небольшие самостоятельные работы. Результаты работ можно увидеть на диаграммах.

Одно из заданий работы

Одно из заданий работы

Предлагаем задачи для самостоятельного решения:

1.Разделить многочлен на

2.Разделить многочлен на .

4. Применение теории делимости

Дата рождения: 31 марта 1730 г

Место рождения: страна Франция, Немур.

Дата смерти:27 сентября 1783.

Научная сфера: теория чисел.

Что и требовалось доказать.

Важнейшим следствием теоремы Безу является то, что корни целочисленного многочлена являются делителями его свободного члена.

Задачи на применение теоремы Безу и следствия из теоремы:

1. Найти остаток от деления многочлена на двучлен .

Решение: Исходя из теоремы Безу, искомый остаток соответствует значению многочлена в точке . Тогда подставляем в выражение для многочлена вместо . Получаем: .

Ответ: остаток равен 5.

2. Найти значение f (x) = x 3 − 3x 2 + 7x − 5 в точке 3.

Решение : Напомним теорему Безу: Значение многочлена f (x) в точке c равно остатку от деления f (x) на (x − c). Разделим f (x) = x 3 − 3x 2 + 7x – 5 на х-3:

Предлагаем задачи для самостоятельного решения:

2. Найти корни многочлена по схеме Горнера: f (x) = x 3 + 2 x 2 – 5 x – 6.

Разложение на множители

Запись нашего решения:

Предлагаем задачи для самостоятельного решения:

Разложить на множители многочлены:

Источник