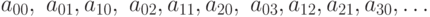Доказать что множество счетно

Математический портал

Nav view search

Navigation

Search

Счетность и несчетность множеств. Равномощность множеств.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Примеры.

Доказать, что следующие множества счетны:

Решение.

Что и требовалось доказать.

Решение.

Что и требовалось доказать.

Решение.

Что и требовалось доказать.

Решение.

Что и требовалось доказать.

Примеры:

Доказательство.

Что и требовалось доказать.

Доказательство.

Проведем доказательство в несколько этапов:

Что и требовалось доказать.

Домашнее задание.

Доказать, что следующие множества счетны:

1.70. Используя результат задачи 1.68, доказать, что множество всех точек плскости с рациональными координатами счетно.

Источник

Счетные множества

Множество называется счетным, если оно равномощно множеству 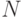натуральных чисел, то есть если его можно представить в виде (здесь — элемент, соответствующий числу ; соответствие взаимно однозначно, так что все различны).

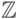
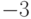
Например, множество целых чисел счетно, так как целые числа можно расположить в последовательность , , , , , , ,

(а) Подмножество счетного множества конечно или счетно.

(в) Объединение конечного или счетного числа конечных или счетных множеств конечно или счетно.

(а) Пусть — подмножество счетного множества . Выбросим из последовательности те члены, которые не принадлежат (сохраняя порядок оставшихся). Тогда оставшиеся члены образуют либо конечную последовательность (и тогда конечно), либо бесконечную (и тогда счетно).

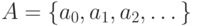
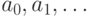
(в) Пусть имеется счетное число счетных множеств Расположив элементы каждого из них слева направо в последовательность ( ) и поместив эти последовательности друг под другом, получим таблицу

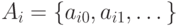
Замечание. В доказательстве утверждения (б) теоремы 2 есть тонкий момент: на каждом шаге мы должны выбрать один из оставшихся элементов множества ; такие элементы есть, но у нас нет никакого правила, позволяющего такой выбор описать. При более формальном построении теории множеств тут нужно сослаться на специальную аксиому, называемую аксиомой выбора. Законность этой аксиомы вызывала большие споры в начале 20-го века, но постепенно к ней привыкли, и эти споры сейчас почти не воспринимаются. В середине века великий логик Курт Гедель доказал, что аксиому выбора нельзя опровергнуть, пользуясь остальными аксиомами теории множеств, а в 1960-е годы американский математик Пол Дж.Коэн доказал, что ее нельзя и вывести из остальных аксиом. (Конечно, понимание этих утверждений требует подробного изложения теории множеств как аксиоматической теории.)

30. Такой же тонкий момент (хотя и менее очевидный) есть и в доказательстве утверждения (в). Можете ли вы догадаться, где он? (Ответ: мы знаем, что множества счетны, то есть что существует взаимно однозначное соответствие между и . Но нужно выбрать и фиксировать эти соответствия, прежде чем удастся построить соответствие между объединением всех и .)

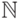
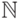
Еще несколько примеров счетных множеств:

31. Докажите, что любое семейство непересекающихся интервалов на прямой конечно или счетно. (Указание: в каждом интервале найдется рациональная точка.)

33. Докажите, что множество точек строгого локального максимума любой функции действительного аргумента конечно или счетно.

Докажите, что множество точек разрыва неубывающей функции Действительного аргумента конечно или счетно.

Источник

06. Теоремы о счетных множествах. Множества мощности континуум

Если рассмотреть любое конечное множество и любое его собственное (непустое и не совпадающее с ним самим) подмножество, то элементов в подмножестве меньше, чем в сам множестве, т. е. часть меньше целого.

Обладают ли бесконечные множества таким свойством? И может ли иметь смысл утверждение, что в одном бесконечном множестве «меньше» элементов, чем в другом, тоже бесконечном? Ведь про два бесконечных множества мы можем пока только сказать, эквивалентны они или нет. А существуют ли вообще неэквивалентные бесконечные множества?

Приведём забавную фантастическую историю из книги Н. Я. Виленкина «Рассказы о множествах». Действие происходит в далёком будущем, когда жители разных галактик могут встречаться друг с другом. Поэтому для всех путешествующих по космосу построена огромная гостиница, протянувшаяся через несколько галактик.

В этой гостинице бесконечно много номеров (комнат), но, как и положено, все комнаты пронумерованы, и для любого Натурального числа n есть комната с этим номером.

Однажды в этой гостинице проходил съезд космозоологов, в котором участвовали представители всех галактик. Так как галактик тоже бесконечное множество, все места в гостинице оказались занятыми. Но в это время к директору гостиницы приехал его друг и попросил поселить его в эту гостиницу.

«После некоторых размышлений директор обратился к администратору и сказал:

– Куда же я дену жильца этого номера? – удивлённо спросил администратор.

– А его переселите в № 2. Жильца же из № 2 отправьте в № 3, из № 3 – в № 4 и т. д.»

Вообще, пусть постоялец, живущий в номере K, переедет в номер K+1, как это показано на следующем рисунке:

Тогда у каждого снова будет свой номер, а № 1 освободится.

Таким образом, нового гостя удалось поселить – именно потому, что номеров в гостинице бесконечно много.

Первоначально участники съезда занимали все номера гостиницы, следовательно, между множеством космозоологов и множеством N Было установлено взаимно однозначное соответствие: каждому космозоологу дали по номеру, на двери которого написано соответствующее ему натуральное число. Естественно считать, что делегатов было «столько же», сколько имеется натуральных чисел. Но приехал ещё один человек, его тоже поселили, и количество проживающих увеличилось на 1. Но их снова осталось «столько же», сколько и натуральных чисел: ведь все поместились в гостиницу!

Мы пришли к удивительному выводу: если к множеству, которое равномощно N, добавить ещё один элемент, получится множество, которое снова равномощно N. Но ведь совершенно ясно, что делегаты-космозоологи представляют собой часть того множества людей, которые разместились в гостинице после приезда нового гостя. Значит, в этом случае часть не «меньше» целого, а «равна» целому!

Итак, из определения эквивалентности (которое не приводит ни к каким странностям в случае конечных множеств) следует, что часть бесконечного множества может быть эквивалентна всему множеству.

Новый постоялец не удивился, когда на другое утро ему предложили переселиться в № 1000000. Просто в гостиницу прибыли запоздавшие космозоологи из галактики ВСК-3472, и надо было разместить ещё 999999 жильцов.

Эта задача оказалась весьма сложной. Но и в этом случае нашёлся выход.

«В первую очередь администратор приказал переселить жильца из № 1 в № 2.

– А жильца из № 2 переселите в № 4, из № 3 – в № 6, вообще, из номера N – в номер 2n.

Определение. Множество А, равномощное множеству натуральных чисел N, называется Счетным множеством (имеет мощность счетного множества). Если множество В является бесконечным и не равномощно множеству N, то его называют несчетным.

Множество, которое является конечным или счетным, еще называют не более чем счетным .

Пусть множество А является счетным. По определению, тогда существует биекция А на N, т. е. каждому аÎА соответствует единственный номер nÎN и множество А обращается в некоторую последовательность <аn>.

Теорема 1. Любое подмножество счетного множества не более чем счетно.

Доказательство. Пусть А = — счетное множество и В Í А. Если В конечное множество, то утверждение доказано. Предположим, что В бесконечное множество. Те элементы А, которые попали в В будут иметь некоторые номера в порядке возрастания: . Тогда необходимая нам биекция, показывающая, что В является счетным множеством, задается в виде: ® k.

Теорема 2. Объединение конечного или счетного числа счетных множеств является счетным множеством.

Теорема 3. Любое бесконечное множество содержит счетное подмножество.

Доказательство. Выберем в заданном множестве А какой-либо элемент, придав ему единичный индекс: а1. Среди всех оставшихся элементов множества А найдется не равный а1 элемент (в силу бесконечности А). Его мы обозначим через а2. Продолжая этот процесс до бесконечности мы получим необходимое нам счетное множество .

Доказательство. Пусть множество М – А не более чем счетно. Тогда множество М = АÈ(М – А) по теореме 2 не более чем счетно. Это противоречит тому, что множество М несчетно и, следовательно, наше исходное предположение не верно. Таким образом, множество М – А несчетно. Последнее еще не означает равномощности множеств М и М – А. Докажем ее. Выделим из М – А счетное множество В. Обозначим через С множество С = (М – А) – В. Справедливы равенства М = АÈВÈС и М – А = ВÈС. Множество АÈВ счетно (теорема 2). Следовательно, существует биекция f из АÈВ на А. Теперь можно построить биекцию g из М на М – А по правилу:

Теорема 5. Если множество С бесконечно, а В не более чем счетно, то множество ВÈС равномощно множеству С.

Доказательство. Если множество С счетно, то множество ВÈС также счетно и следовательно они равномощны. Если же множество С не счетно, то мы можем воспользоваться теоремой 4, положив в ней А = СÇВ, а М = С.

Теорема 6. Если множество С является бесконечным, то существует его подмножество В такое, что В¹С и В равномощно с С.

Доказательство. По теореме 3 мы можем выделить из множества С его счетное подмножество А. Если множество С счетно, то в качестве В из утверждения теоремы можно взять В=А. Если же С не счетно, то можно положить В=С-А и утверждаемое вытекает из теоремы 4.

Теорема 7. Множество рациональных чисел Q является счетным.

Доказательство. Обозначим через Р множество всех пар натуральных чисел (p, q), таких что p и q не имеют общих целых делителей, кроме единицы. Для пары натуральных чисел (p, q) введем ее высоту m = p + q. Обозначим Рn множество пар натуральных чисел высоты n. Нетрудно проверить, что каждое множество Рn является конечным и содержит не более, чем n-1 член. Так как Р = Èn Рn, то множество Р счетно в силу теоремы 2.

Теорема 8. Множество точек интервала (0,1) является несчетным.

Доказательство (Диагональный метод Кантора). Доказательство проведем от противного, предположив, что множество точек интервала (0,1) является счетным. Тогда все точки можно записать в виде последовательности:

Множества, равномощные множеству точек интервала (0, 1), называются множествами мощности Континуум .

Задачи.

1. Показать, что если множества А и В являются счетными, то и их произведение А´В является счетным.

2. Установить биекцию между множеством N всех натуральных чисел и множеством Q всех четных положительных чисел.

3. Установить биекцию между множеством N всех натуральных чисел и множеством Р всех четных чисел.

Источник

Счетные множества

Множество называется счетным, если оно равномощно множеству 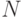натуральных чисел, то есть если его можно представить в виде (здесь — элемент, соответствующий числу ; соответствие взаимно однозначно, так что все различны).

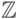
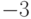
Например, множество целых чисел счетно, так как целые числа можно расположить в последовательность , , , , , , ,

(а) Подмножество счетного множества конечно или счетно.

(в) Объединение конечного или счетного числа конечных или счетных множеств конечно или счетно.

(а) Пусть — подмножество счетного множества . Выбросим из последовательности те члены, которые не принадлежат (сохраняя порядок оставшихся). Тогда оставшиеся члены образуют либо конечную последовательность (и тогда конечно), либо бесконечную (и тогда счетно).

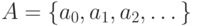
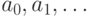
(в) Пусть имеется счетное число счетных множеств Расположив элементы каждого из них слева направо в последовательность ( ) и поместив эти последовательности друг под другом, получим таблицу

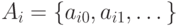
Замечание. В доказательстве утверждения (б) теоремы 2 есть тонкий момент: на каждом шаге мы должны выбрать один из оставшихся элементов множества ; такие элементы есть, но у нас нет никакого правила, позволяющего такой выбор описать. При более формальном построении теории множеств тут нужно сослаться на специальную аксиому, называемую аксиомой выбора. Законность этой аксиомы вызывала большие споры в начале 20-го века, но постепенно к ней привыкли, и эти споры сейчас почти не воспринимаются. В середине века великий логик Курт Гедель доказал, что аксиому выбора нельзя опровергнуть, пользуясь остальными аксиомами теории множеств, а в 1960-е годы американский математик Пол Дж.Коэн доказал, что ее нельзя и вывести из остальных аксиом. (Конечно, понимание этих утверждений требует подробного изложения теории множеств как аксиоматической теории.)

30. Такой же тонкий момент (хотя и менее очевидный) есть и в доказательстве утверждения (в). Можете ли вы догадаться, где он? (Ответ: мы знаем, что множества счетны, то есть что существует взаимно однозначное соответствие между и . Но нужно выбрать и фиксировать эти соответствия, прежде чем удастся построить соответствие между объединением всех и .)

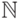
Еще несколько примеров счетных множеств:

31. Докажите, что любое семейство непересекающихся интервалов на прямой конечно или счетно. (Указание: в каждом интервале найдется рациональная точка.)

33. Докажите, что множество точек строгого локального максимума любой функции действительного аргумента конечно или счетно.

Докажите, что множество точек разрыва неубывающей функции Действительного аргумента конечно или счетно.

Источник

Теория функций действительного переменного/Счётные множества

Доказательство проиллюстрируем следующим рисунком (в отличие от русской матем.символики здесь «/» обозначает не дробь, а стоит вместо запятой, обозначая упорядоченную пару-элемент N*N):

В результате расстановки, указанной стрелками, все элементы приобретут номер, и, значит, это множество- счётное.

Теорема 2: Декартово произведение конечного числа счетных множеств есть множество счетное.

Теорема 3: Всякое бесконечное множество содержит счетное подмножество.

Теорема 4: Всякое бесконечное подмножество счётного множества счётно.

Пусть множество A счётно, а B— его бесконечное подмножество. По предыдущей теореме множество B содержит счётное подмножество C. Так как множества A и C оба счётны, то они эквивалентны:A

A, то есть множество B эквивалентно счётному множеству и потому само счётно.

Теорему 4 можно перефразировать следующим образом: 4′ : Всякое подмножество счётного множества конечно или счётно.

Теорема 5: При любом отображении образ счётного множества конечен или счётен.

Теорема 7: Всякое семейство < Δ x >x ∈ X <\displaystyle \<\Delta _\>_> попарно не пресекающихся непустых интервалов конечно или счётно.

Теорема 8: Объединение конечной или счётной совокупности конечных или счётных множеств конечно или счётно.

Занумеруем элементы множества A_n в последовательность

причём, если A_n конечно и содержит k_n элементов, то будем считать, что первые k_n членов этой последовательности попарно различны и исчерпывают всё множество A_n, а для m>k_n, полагаем a_nm=a_nkn.

Примеры представления в форме последовательности некоторых объединений:

Теорема 9: Множество всех алгебраических чисел счетно

Замечание: Из теоремы 10 следует, что всякое бесконечное множество содержит эквивалентное ему собственное подмножество, конечное же множество таким свойством не обладает. Поэтому свойство множества иметь эквивалентную ему правильную часть можно принять за определение бесконечного множества.

Источник