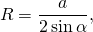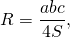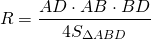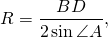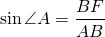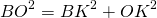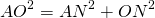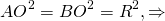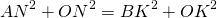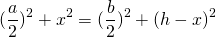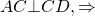Доказать что около равнобедренной трапеции можно описать окружность
Доказать что около равнобедренной трапеции можно описать окружность
Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.
$$ 4.<2>^<○>$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).
$$ 4.<3>^<○>$$. В равнобокой трапеции углы при основании равны (рис. 22).
$$ 4.<4>^<○>$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).
$$ 4.<5>^<○>$$. В равнобокой трапеции диагонали равны (рис. 24).
$$ 4.<6>^<○>$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме
(рис. 25, основания равны `a` и `b`, `a>b`).
$$ 4.<7>^<○>$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).
$$ 4.<8>^<○>$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).
Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.
$$ 4.<10>^<○>$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).
$$ 4.<11>^<○>$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.
Применяем теорему косинусов (см. рис. 29а и б):
`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,
`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).
Проводим `CK«|\|«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:
| `d_1^2+d_2^2=c_1^2+c_2^2+2ab`. |
В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем
Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.
Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то
Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.
Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна
Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).
Найти радиус окружности, описанной около этой трапеции.
Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда
$$ 4.<12>^<○>$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.
Радиус описанной окружности трапеции
Как найти радиус описанной окружности для трапеции?
В зависимости от данных условия, сделать это можно разными способами. Готовой формулы радиуса описанной около трапеции окружности нет.
I. Радиус описанной около трапеции окружности как радиус окружности, описанной около треугольника, вершины которого — вершины трапеции
Описанная около трапеции окружность проходит через все её вершины, следовательно, является описанной для любого из треугольников, вершины которых являются вершинами трапеции.
В общем случае радиус описанной около треугольника окружности может быть найден по одной из формул
где a — сторона треугольника, α — противолежащий ей угол;
где a, b, c — стороны, S — площадь треугольника.
Для трапеции ABCD радиус может быть найден, например, как радиус окружности, описанной около треугольника ABD:
где синус угла A можно найти из прямоугольного треугольника ABF:
III. Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров
Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции. (Можно рассуждать иначе: в равнобедренном треугольнике AOD (AO=OD=R) высота ON является также медианой. Для треугольника BOC — аналогично).
Если известна высота трапеции KN=h, основания AD=a, BC=b, можно обозначить ON=x.
Если центр окружности лежит внутри трапеции, OK=h-x, из прямоугольных треугольников ANO и BKO можно выразить
и приравнять правые части
Решив это уравнения относительно x, можно найти R.
IV. Если диагональ трапеции перпендикулярна боковой стороне, центр описанной окружности лежит на середине большего основания и радиус равен половине большего основания.
точка O — середина AD
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной окружности лежит вне трапеции, за большим основанием.
I вариант нахождения радиуса для этого случая не изменяется.
Во II случае OK=h+x, соответственно, изменяется уравнение для нахождения x и R.
Позже рассмотрим конкретные задачи нахождения радиуса описанной около трапеции окружности.
Материал по геометрии на тему «трапеция и ее свойства»
ФГКОУ «МКК «Пансион воспитанниц МО РФ»
Руководитель отдельной дисциплины
(математика, информатика и ИКТ)
Ю. В. Крылова _____________
«___» _____________ 2015 г.
« Трапеция и ее свойства »
Шаталиной Елены Дмитриевны
рекомендовано к использованию
на заседании ПМО от _______________
Свойства равнобедренной трапеции 4
Вписанные и описанные окружности 7
Свойства вписанных и описанных трапеций 8
Средние величины в трапеции 12
Свойства произвольной трапеции 15
Признаки трапеции 18
Дополнительные построения в трапеции 20
Площадь трапеции 25
. Список используемой литературы
Доказательства некоторых свойств трапеции 27
Задачи для самостоятельных работ
Задачи по теме «Трапеция» повышенной сложности
Проверочный тест по теме «Трапеция»
Данная работа посвящена геометрической фигуре, которая называется трапеция. «Обычная фигура»,- скажете вы, но это не так. Она таит в себе много тайн и загадок, если приглядеться и углубиться в ее изучение, то вы откроете для себя много нового в мире геометрии, задачи, которые раньше не решались, покажутся вам легкими.
В работе рассматриваются свойства знакомые воспитанницам по пройденному материалу в учебнике, но в большей степени неизвестные свойства, которые необходимы для решения сложных задач. Чем больше количество решаемых задач, тем больше вопросов возникает при решении их. Ответом на эти вопросы иногда кажется тайной, узнавая, новые свойства трапеции, необычные приемы решения задач, а также технику дополнительных построений, мы постепенно открываем тайны трапеции. В интернете, если забить в поисковике, о методах решения задач по теме «трапеция» очень мало литературы. В процессе работы над проектом найден большой объем информации, которая поможет воспитанницам в глубоком изучении геометрии.
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
У
глы при основании равнобедренной трапеции равны.
С
умма углов трапеции, прилежащих к ее боковой стороне, а также противоположных углов равнобедренной трапеции равна 180°.
3. Диагонали равнобедренной трапеции равны.
Отрезки, последовательно соединяющие середины смежных сторон равнобедренной трапеции, образуют ромб.
В равнобедренной трапеции прямая, проходящая через середины оснований, перпендикулярна им и является осью симметрии трапеции.
Если диагонали равнобедренной трапеции перпендикулярны, то высота трапеции равна средней линии.
Около равнобедренной трапеции можно описать окружность.
В равнобедренной трапеции квадрат диагонали равен квадрату его боковой стороны плюс произведение оснований: d 2 = c 2 + a • b
1
0. Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований, а проекция диагонали равна помусумме оснований.
3. Вписанная и описанная окружность
Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность.
Е
сли трапеция равнобедренная, то около неё можно описать окружность.
Если в равнобокую трапецию можно вписать окружность, то средняя линия трапеции равна боковой стороне.
2.Если в равнобедренную трапецию можно вписать окружность, то
Е сли в трапецию вписана окружность, которая касается одной из боковых сторон, разбивает ее на отрезки m и n, тогда радиус вписанной окружности равен среднему геометрическому этих отрезков.
Е
сли в равнобокую трапецию вписана окружность, то высота трапеции есть среднее геометрическое ее оснований.
Если в трапецию можно вписать окружность и около трапеции можно описать окружность, то проекция диагонали на большее основание, равна боковой стороне и равна средней линии трапеции.
Если в трапецию вписана окружность, то вершина трапеции, центр вписанной в нее окружности и основание перпендикуляра, опущенного из другой вершины на основание, лежат на одной прямой.
Если диагонали вписанной в окружность трапеции (четырехугольника) взаимно перпендикулярны, то сумма квадратов его противоположных сторон равна квадрату диаметра описанной окружности или удвоенному квадрату боковой стороны: a 2 + b 2 = 4 R 2 = 2 c 2
5. Средние величины в трапеции
Р
адиус окружности, вписанной в трапецию, есть среднее геометрическое произведения отрезков боковой стороны трапеции, на которые она разбивается точкой касания.
Если в равнобедренную трапецию вписана окружность, то высота трапеции есть среднее геометрическое произведения оснований трапеции
В
любой трапеции с основаниями a и b отрезок, параллельный основаниям, концы которого лежат на боковых сторонах, равен среднему арифметическому оснований , если он соединяет середины боковых сторон (т.е. является средней линией трапеции). MN = ( a + b )/ 2 .
В
любой трапеции с основаниями a и b отрезок, параллельный основаниям, концы которого лежат на боковых сторонах, равен среднему гармоническому оснований , если он проходит через точку пересечения диагоналей KL =2 ab /( a + b )
В любой трапеции с основаниями a и b отрезок, параллельный основаниям, концы которого лежат на боковых сторонах, равен среднему геометрическому оснований , если он делит трапецию на две трапеции, подобные между собой.
В
любой трапеции с основаниями a и b отрезок, параллельный основаниям, концы которого лежат на боковых сторонах, равен среднему квадратичному оснований , если он делит трапецию на две трапеции равной площади (равновеликие).
b ˂ h ˂ g ˂ m ˂ s ˂ a
6. Свойства произвольной трапеции
1 
. Середины диагоналей трапеции и середины боковых сторон лежат на одной прямой.
2. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.
3. Отрезки прямой, параллельной основаниям трапеции, пересекающей боковые стороны и диагонали трапеции, заключенные между боковой стороной диагональю, равны.
Точка пересечения продолжения боковых сторон произвольной трапеции, точка пересечения ее диагоналей и середин оснований лежат на одной прямой.
5. При пересечении диагоналей произвольной трапеции образуются четыре треугольника с общей вершиной, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики(т.е. имеют равные площади).
6. Сумма квадратов диагоналей произвольной трапеции равна сумме квадратов боковых сторон, сложенной с удвоенным произведением оснований.
d 1 2 + d 2 2 = c 2 + d 2 + 2 ab
7 
. В прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований d 1 2 — d 2 2 = a 2 – b 2
8 . Прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
9
. Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам.
Ч
етырехугольник является трапецией тогда и только тогда, когда при его диагональном разбиении ровно два противолежащих треугольника равновелики. При этом квадрат площади каждого из них равен произведению площадей смежных с ним треугольников
Если средняя линия четырехугольника равна полусумме противолежащих ей сторон, то четырехугольник является трапецией (или параллелограммом). Если m = ( a + b )/2, то ABCD – трапеция (или параллелограмм)
Т
рапеция является равнобедренной, если углы при одном из оснований равны.
Если около трапеции можно описать окружность, то трапеция является равнобедренной
2
. Отрезок, параллельный одной из боковых сторон трапеции, один конец которого совпадает с серединой другой боковой стороны, другой принадлежит прямой, содержащей основание.
3
. Если даны все стороны трапеции, через вершину меньшего основания проводится прямая, параллельная боковой стороне. Получается треугольник со сторонами, равными боковым сторонам трапеции и разности оснований. По формуле Герона находят площадь треугольника, потом высоту треугольника, которая равна высоте трапеции.
4
. Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.
5. Высоты трапеции, опущенные из вершин одного основания, высекают на прямой, содержащей другое основание, отрезок, равный первому основанию.
6
. Отрезок, параллельный одной из диагоналей трапеции проводится через вершину – точку, являющуюся концом другой диагонали. В результате получается треугольник с двумя сторонами, равными диагоналям трапеции, и третьей – равной сумме оснований
7
.Отрезок, соединяющий середины диагоналей, равен полуразности оснований трапеции.
8. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, они перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.
9. Биссектриса угла трапеции отсекает равнобедренный треугольник.
1
0. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.
1
1. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.
9. Площадь трапеции
П
лощадь трапеции равна произведению средней линии трапеции на высоту S = m • h .
2. Площадь трапеции равна произведению боковой стороны и перпендикуляра, проведенного из середины другой боковой стороны к прямой, содержащей первую боковую сторону.
П
лощадь равнобедренной трапеции, диагонали которой перпендикулярны. Если диагонали равнобедренной трапеции перпендикулярны, то площадь трапеции равна квадрату средней л инии трапеции или квадрату высоты трапеции. S = h 2
Площадь равнобедренной трапеции с радиусом вписанной окружности равным r и углом при основании α:
ГДЕ, КАК И ДЛЯ ЧЕГО ИСПОЛЬЗЕУТСЯ ТРАПЕЦИЯ?
Трапеция в моде: Трапеция в одежде была популярна ещё в средние века, в романскую эпоху IX-XI вв. В тот период основу женской одежды составляли туники в пол, к низу туника сильно расширялась, что и создавало эффект трапеции. Возрождение силуэта произошло в 1961-ом году и стало гимном молодости, независимости и утонченности. Огромную роль в популяризации трапеции сыграла хрупкая модель Лесли Хорнби, известная, как Твигги. Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции.
Трапеция в природе: трапеция встречается и в природе. У человека есть трапециевидная мышца, у некоторых людей лицо имеет форму трапеции. Лепестки цветов, созвездия, и конечно же вулкан Килиманджаро тоже имеют форму трапеции.
Трапеция в быту: Трапеция используется и в быту, т.к ее форма практична. Она встречается в таких предметах как: ковш экскаватора, стол, винт, машина.
Трапеция в технике: Трапеция используется при конструировании деталей в космических технологиях и в авиации. Например, некоторые солнечные батареи космических станций имеют форму трапеции так как имеют большую площадь, значит накапливают больше солнечной эн
В 21 первом веке люди уже практически не задумываются о значении геометрических фигур в их жизни. Их совершенно не волнует какой формы у них стол, очки или телефон. Они просто выбирают ту форму, которая практична. Но именно от формы той или иной вещи может зависеть использование предмета, его предназначение, результат работы. Сегодня мы познакомили вас с одной из величайших достижений человечества- с трапецией. Мы приоткрыли вам дверь в удивительный мир фигур, поведали вам тайны трапеции и показали, что геометрия вокруг нас.
Список используемой литературы
Болотов А.А., Прохоренко В.И., Сафонов В.Ф., Математика Теория и Задачи. Книга 1 Учебное пособие для абитуриентов М.1998 Издательство МЭИ.
Быков А.А, Малышев Г.Ю., ГУВШ факультет довузовской подготовки. Математика. Учебно-методическое пособие 4 часть М2004
Гордин Р.К. Планиметрия. Задачник.
Иванов А.А. Иванов А.П, Математика: Пособие для подготовки к ЕГЕ и поступлению в вузы-М : Издательство МФТИ,2003-288с. ISBN 5-89155-188-3
Пиголкина Т.С, Министерство образования и науки РФ федеральное государственное бюджетное образовательное учреждение дополнительного образования детей «ЗФТШ Московского физико-технического института (государственного университета)». Математика. Планиметрия. Задания №2 для 10-ых классов (2012-2013 учебный год).
Пиголкина Т.С., Планиметрия (часть1).Матиматическая Энциклопедия Абитуриента. М., издательство российского открытого университета 1992.
Шарыгин И.Ф.Избранные задачи по геометрии конкурсных экзаменов в ВУЗЫ (1987-1990) Львов Журнал «Квантор» 1991.
Энциклопедия «Аванта плюс», Математика М., Мир энциклопедий Аванта 2009.
1.Доказательство некоторых свойств трапеции.
1. Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках K и L . Доказать, что если основания трапеции равны а и b , то длина отрезка KL равна среднему геометрическому оснований трапеции. Доказательство
( 1 )
∆ COB по двум углам. тогда: 
т.е. 
( 2 )
Аналогично LO = 
Тогда K L = KO + LO = 
В о всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжения боковых сторон лежат на одной прямой.
Доказательство: Пусть продолжения боковых сторон пересекаются в точке К. Через точку К и точку О пересечения диагоналей проведём прямую КО.
окажем, что эта прямая делит основания пополам.
О
бозначим ВМ = х, МС = у, AN = и, ND = v . Имеем:
∆AKN → 
∆NKD → 
→
N
∆ BMO 
∆DNO 
∆ CMO ∆ ANO 
поэтому 
.
Перемножая полученные равенства, получим 
, откуда следует