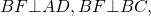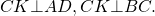Доказать что трапеция равнобедренная если углы при основании равны диагонали трапеции равны

Если у трапеции углы при основании равны

(I признак равнобедренной трапеции).

Если у трапеции углы при основании равны, то она — равнобедренная.

Дано : ABCD — трапеция,

Доказать: ABCD — равнобедренная.

1) Проведем высоты трапеции BF и CK:

2) Рассмотрим треугольники ABF и DCK.

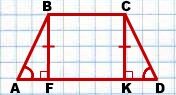
∠AFB=90º, ∠DKC=90º (так как BF и CK — высоты трапеции).

BF=CK (как высоты трапеции).

Следовательно, треугольники ABF и DCK равны (по катету и острому углу).

3) Из равенства треугольников следует равенство соответствующих сторон: AB=CD.

Следовательно, трапеция ABCD — равнобедренная ( по определению).

∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB),

∠D+∠C =180º (как внутренние односторонние при AD ∥ BC и секущей CD).

Таким образом, из равенства углов при меньшем основании следует равенство углов и при большем основании трапеции. Уже доказали, что в этом случае трапеция — равнобедренная.

Источник

«Трапеция». 8-й класс

Разделы: Математика

Класс: 8

Ход урока

I. Организационный момент.

II. Актуализация знаний.

Ключевое слово кроссворда – является темой нашего урока.

III. Новый материал.

Трапеция – (от греч. trapezion, букв. – столик).

Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие – непараллельные. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Равнобедренная – трапеция, у которой равны боковые стороны.

Прямоугольная – трапеция, один из углов которой прямой.

Средняя линия трапеции.
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Группы с четными номерами – исследуют диагонали равнобедренной трапеции. Группы с нечетными номерами – исследуют углы равнобедренной трапеции.

Выслушать и обсудить результаты исследования, на доске и в тетрадях записать решения.

Свойства равнобедренной трапеции.

Теорема. В равнобедренной трапеции углы при каждом основании равны.

Проведем СЕ АВ.

ABCD – параллелограмм (АВ СЕ, ВС AD).

CD = AB = CE, СDE – равнобедренный, СDЕ = СЕD.

АВ СЕ, тогда СЕD = ВАЕ, СDЕ = СЕD = ВАЕ.

ABC = 180° – СDЕ = 180° – ВАЕ = BCD.

Теорема. В равнобедренной трапеции диагонали равны.

ABC = DСВ (АВ = С, ВС – общая сторона, АВС = ВСD) тогда АС = ВD.

Сформулируйте утверждения, обратные свойствам, и выясните их справедливость.

Признаки равнобедренной трапеции.

Выслушать и обсудить результаты исследования, на доске и в тетрадях записать решения.

1. Если углы при основании трапеции равны, то она равнобедренная.

Проведем ЕС АВ.

ABCЕ – параллелограмм, тогда АВ СЕ, А = СЕD, СЕD – равнобедренный (D = СЕD), тогда СЕ = СD.

АВ = СЕ = СD, тогда АВСD – равнобедренная трапеция.

2. Если диагонали трапеции равны, то она равнобедренная.

Проведем СК ВD.

ВСКD – параллелограмм (т.к. СК ВD, ВС АК).

АСК – равнобедренный, т.к. АС = ВD = СК, САD = СDА.

СК ВD, ВDА = СКD, тогда САD = СКD.

АВD = DСА, т.к. АС=ВD, АD – общая сторона, САD = СКD, тогда АВ = СD, т.е. АВСD – равнобедренная трапеция.

Источник

Рассмотрим два прямоугольных треугольника АВВ1 и ДСС1.

Углы АВВ1 = ДСС1 = 90 градусов ; углы ВАВ1 = СДС1 ; ВВ1 = СС1(как высоты в трапеции).

Как известно, для подобия прямоугольных треугольников достаточно, чтобы они имели по равному острому углу и равному катету ⇒ ΔАВВ1 = ΔДСС1 ⇒ АВ = СД⇒

Рассмотрим треугольники АВО и ДСО.

По первому признаку равенства треугольников ΔАВО = ΔДСО⇒АВ = СД⇒трапеция

Докажите что у равнобедренной трапеции углы при основании равны?

Докажите что у равнобедренной трапеции углы при основании равны.

Докажите что в равнобедренной трапеции 1)углы при каждом основании равны 2) диагонали равны?

Докажите что в равнобедренной трапеции 1)углы при каждом основании равны 2) диагонали равны.

Равнобедренная трапецияРавнобокой (равнобедренной) называется трапеция с равными боковыми сторонами?

Равнобокой (равнобедренной) называется трапеция с равными боковыми сторонами.

Свойства равнобедренной трапеции

Углы при одном основании равнобедренной трапеции равны.

Только около равнобедренной трапеции можно описать окружность ; она совпадает с окружностью, описанной около любого треугольника с вершинами в вершинах трапеции.

Её центр лежит на серединном перпендикуляре к основаниям трапеции.

Если центр описанной окружности лежит на основании трапеции, то ее диагональ перпендикулярна боковой стороне.

Докажите, что если в трапеции диагонали равны, то трапеция равнобедренная?

Докажите, что если в трапеции диагонали равны, то трапеция равнобедренная.

Выполните необходимые построения.

Докажите, что в равнобедренной трапеции, диагонали равны?

Докажите, что в равнобедренной трапеции, диагонали равны.

Докажите что в равнобедренной трапеции диагонали равны?

Докажите что в равнобедренной трапеции диагонали равны.

Докажите, что трапеция равнобедренная, если диоганали трапеции равны?

Докажите, что трапеция равнобедренная, если диоганали трапеции равны.

Докажите, что в равнобедренной трапеции углы при основании равны?

Докажите, что в равнобедренной трапеции углы при основании равны.

НАЙДИТЕ ОСНОВАНИЯ ТРАПЕЦИЙ 2)ДИАГОНАЛИ РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫ.

1) прямой 2) тупой 3) острый.

Можно например так. Точку В поставь где хочешь.

Источник