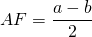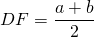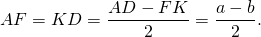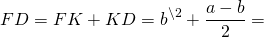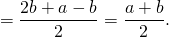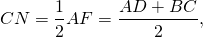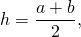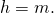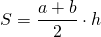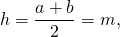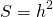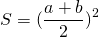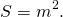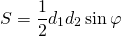Доказать что в равнобедренной трапеции высота равна полусумме оснований
Высота равнобедренной трапеции
Это свойство равнобедренной трапеции удобно доказать в общем виде в начале изучения темы, чтобы в дальнейшем использовать его при решении задач.
Высота равнобедренной трапеции, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.



2) Четырехугольник ABCD — прямоугольник (так как у него все углы прямые). Следовательно, его противоположные стороны равны: FK=BC=b.
3) Рассмотрим треугольники ABF и DCK.
∠AFB=90º, ∠DKC=90º (так как BF и CK — высоты трапеции).
BF=CK (как высоты трапеции).
Следовательно, треугольники ABF и DCK равны (по катету и гипотенузе).
Из равенства треугольников следует равенство соответствующих сторон:
Что и требовалось доказать.
Поскольку средняя линия трапеции равна полусумме ее оснований, длина отрезка FD равна длине среднее линии трапеции.
Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции
Признаки равнобедренной трапеции
∠ABC = ∠BCD и ∠BAD = ∠ADC
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
Основные свойства равнобедренной трапеции
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD
Стороны равнобедренной трапеции
Формулы длин сторон равнобедренной трапеции:
a = b + 2 h ctg α = b + 2 c cos α
3. Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | — b b = | 2S | — a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
| с = | S |
| m sin α |
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
| с = | 2S |
| ( a + b ) sin α |
Средняя линия равнобедренной трапеции
Формулы длины средней линии равнобедренной трапеции:
2. Формула средней линии трапеции через площадь и сторону:
| m = | S |
| c sin α |
Высота равнобедренной трапеции
Формулы определения длины высоты равнобедренной трапеции:
Диагонали равнобедренной трапеции
Формулы длины диагоналей равнобедренной трапеции:
4. Формула длины диагонали через высоту и основания:
| d 1 = | 1 | √ 4 h 2 + ( a + b ) 2 |
| 2 |
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
2. Формула площади через стороны и угол:
3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площади через основания и угол между основой и боковой стороной:
| S = | ab | = | ab |
| sin α | sin β |
5. Формула площади ранобедренной трапеции в которую можно вписать окружность:
S = ( a + b ) · r = √ ab ·c = √ ab ·m
6. Формула площади через диагонали и угол между ними:
| S = | d 1 2 | · sin γ | = | d 1 2 | · sin δ |
| 2 | 2 |
7. Формула площади через среднюю линию, боковую сторону и угол при основании:
S = mc sin α = mc sin β
Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Узнать ещё
Знание — сила. Познавательная информация
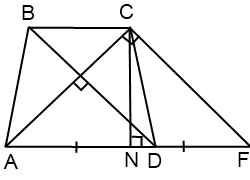
В равнобедренной трапеции диагонали перпендикулярны
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм ( BC ∥ DF как основания трапеции, BD ∥ CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
sin 90 º =1, и диагонали равнобедренной трапеции равны, то площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна
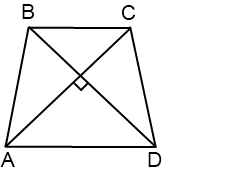
Свойства равнобедренной (равнобокой) трапеции
В данной публикации мы рассмотрим определение и основные свойства равнобедренной трапеции.
Напомним, трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны, т.е. AB = CD.
Свойство 1
Углы при любом из оснований равнобедренной трапеции равны.
Свойство 2
Сумма противоположных углов трапеции равняется 180°.
Для рисунка выше: α + β = 180°.
Свойство 3
Диагонали равнобедренной трапеции имеют одинаковую длину.
Свойство 4
Высота равнобедренной трапеции BE, опущенная на основание большей длины AD, делит его на два отрезка: первый равняется половине суммы оснований, второй – половине их разности.
Свойство 5
Отрезок MN, соединяющий середины оснований равнобокой трапеции, перпендикулярен этим основаниям.
Прямая, проходящая через середины оснований равнобедренной трапеции, называется ее осью симметрии.
Свойство 6
Вокруг любой равнобедренной трапеции можно описать окружность.
Свойство 7
Если сумма оснований равнобокой трапеции равно удвоенной длине ее боковой стороны, в нее можно вписать окружность.
Радиус такой окружности равняется половине высоты трапеции, т.е. R = h/2.
Примечание: остальные свойства, которые применимы ко всем видам трапеций, приведены в нашей публикации – “Что такое трапеция: определение, виды, свойства”.
Доказать что в равнобедренной трапеции высота равна полусумме оснований
Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.
$$ 4.<2>^<○>$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).
$$ 4.<3>^<○>$$. В равнобокой трапеции углы при основании равны (рис. 22).
$$ 4.<4>^<○>$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).
$$ 4.<5>^<○>$$. В равнобокой трапеции диагонали равны (рис. 24).
$$ 4.<6>^<○>$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме
(рис. 25, основания равны `a` и `b`, `a>b`).
$$ 4.<7>^<○>$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).
$$ 4.<8>^<○>$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).
Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.
$$ 4.<10>^<○>$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).
$$ 4.<11>^<○>$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.
Применяем теорему косинусов (см. рис. 29а и б):
`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,
`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).
Проводим `CK«|\|«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:
| `d_1^2+d_2^2=c_1^2+c_2^2+2ab`. |
В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем
Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.
Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то
Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.
Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна
Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).
Найти радиус окружности, описанной около этой трапеции.
Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда
$$ 4.<12>^<○>$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.