Доказать что выражение является тавтологией

04. Тавтология и противоречие

Определение. Тавтологией Называется составное высказывание, истинное при Всех Наборах истинностных значений составляющих его простых высказываний.

Определение. Противоречием называется составное высказывание, ложное при Всех Наборах истинностных значений составляющих его простых высказываний.

Пример. Доказать, что высказывание является тавтологией, а высказывание – противоречием.

Решение. Для доказательства составим общую таблицу истинности для этих формул.

При всех истинностных значениях высказывания А высказывание принимает истинное значение, значит, является тавтологией. При всех истинностных значениях высказывания А высказывание принимает ложное значение, значит, является противоречием. □

Теорема 1.3. Отрицанием тавтологии является противоречие, отрицанием противоречия является тавтология.

Доказательство. 1) Рассмотрим формулу, являющуюся тавтологией. По определению, при всех наборах истинностных значений составляющих её простых высказываний она принимает значение «истина». Тогда, по определению, отрицание данной формулы при всех наборах истинностных значений составляющих её простых высказываний принимает значение «ложь». Значит, отрицание тавтологии является противоречием.

2) Рассмотрим формулу, являющуюся противоречием. По определению, при всех наборах истинностных значений составляющих её простых высказываний она принимает значение «ложь». Тогда, по определению, отрицание данной формулы при всех наборах истинностных значений составляющих её простых высказываний принимает значение «истина». Значит, отрицание противоречия является тавтологией. ■

Задачи и упражнения

1.14. Докажите, что следующие составные высказывания являются тавтологиями:

1) ;

2) ;

3) ;

4) ;

5) .

1.15. Докажите, что следующие составные высказывания являются противоречиями:

1) ; 2) ; 3) .

Источник

1. Высказывания, формулы, тавтологии

Определение. Высказыванием называется утверждение, которое является истинным или ложным (но не одновременно).

То есть, чтобы выяснить, является ли некоторое предложение высказыванием, нужно сначала убедиться, что это утверждение, а затем установить, истинно оно или ложно.

Пример. “Москва – столица России” – истинное высказывание.

“5 –четное число” – ложное высказывание.

“” – не высказывание (неизвестно, какие значения принимает ).

“Студент второго курса” не высказывание (не является утверждением).

Высказывания бывают элементарные и составные.

Элементарные высказывания не могут быть выражены через другие высказывания. Составные высказывания можно выразить с помощью элементарных высказываний.

Пример. “Число 22 четное” – элементарное высказывание.

“Число 22 четное и делится на 11” – составное высказывание.

Высказывания обозначают заглавными буквами латинского алфавита: , , ,… Эти буквы называют логическими Атомами.

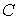
При фиксированном множестве букв Интерпретацией называется функция , которая отображает множество во множество истинностных (логических) значений , то есть .

Истинностные значения истина и ложь сокращенно обозначаются и, л или T, F, или 1,0. Мы будем использовать обозначения 1 и 0. В определенной интерпретации буквы принимают значения 1 или 0.

К высказываниям и буквам можно применять известные из курса дискретной математики логические связки или логические операции. При этом получаются Формулы (формы). Формулы становятся высказываниями при подстановке всех значений букв.

Таблицы истинности основных логических операций.

Более строго формула определяется так.

Определение. 1) Всякая буква есть формула.

2) Если , — формулы, то формулами являются также , , , , .

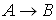
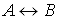
3) Символ является формулой тогда и только тогда, когда это следует из 1) и 2).

В классической логике формулы принято заключать в круглые скобки, но в мы этого делать не будем. Для всякой формулы можно построить таблицу истинности.

Значение формулы 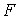в заданной интерпретации обозначают (или , или ).

Часть формулы, которая сама является формулой, называется Подформулой данной формулы.

Определение. Формула называется Тавтологией, если она принимает только истинные значения при любых значениях букв.

Другими словами, тавтология – это тождественно истинная формула.

Установить, является ли формула тавтологией, можно:

– по таблице истинности,

– используя свойства логических операций.

Из курса дискретной математики известны основные логические эквивалентности (свойства логических операций), которые являются примерами тавтологий.

1. Коммутативность: , .

, .

, .

4. Идемпотентность: , .

5. Закон двойного отрицания: .

6. Закон исключения третьего: .

7. Закон противоречия: .

8. Законы де Моргана:

, .

9. Свойства операций с логическими константами:

, , , .

Здесь , и – любые буквы.

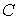
Примеры. 1. Доказать, что формула 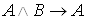является тавтологией.

Доказательство. Допустим, что при некоторых значениях букв (то есть в некоторой интерпретации)

Приходим к противоречию, которое доказывает, что исходная формула – тавтология.

2. Доказать, что формула является тавтологией.

Доказательство. Эквиваленция истинна, если левая и правая части принимают одинаковые значения на некотором наборе значений букв.

Допустим, что при некоторых значениях букв

Следовательно, исходная формула – тавтология.

3. Доказать, что формула является тавтологией.

Доказательство. Допустим, что при некоторых значениях букв

Следовательно, исходная формула – тавтология.

Таким образом, тождественную истинность импликации удобно доказывать от противного, а тождественную истинность эквиваленции установлением равенства значений левой и правой части.

Теорема. Пусть формулы и – тавтологии. Тогда формула – тавтология.

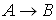
Доказательство. Пусть , , …, – буквы в формулах и . В теории булевых функций было доказано, что все булевы функции, а, следовательно, и формулы, можно считать зависящими от одного и того же количества букв. Рассмотрим некоторый набор значений , , …, , где , . Подставим данный набор значений в формулы и вместо соответствующих букв. Формулы являются тавтологиями по условию теоремы, следовательно, и . По таблице истинности импликации получаем, что . Поскольку набор значений , , …, был произволен, формула – тавтология, что и требовалось доказать.

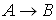
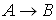
Теорема. Пусть формула – тавтология, , , …, – буквы в формуле , , , …, – любые формулы. Тогда новая формула – тавтология.

Доказательство аналогично доказательству предыдущей теоремы.

Источник

4.1. Введение в логику высказываний

Определение. Высказыванием называется повествовательное предложение, о котором имеет смысл говорить, что оно истинно или ложно.

Примеры высказываний: «2х2=4», «Волга впадает в Черное море», «Москва – столица России». Первое и третье высказывания истинны, второе – ложно. Предложение «Х + Y = 4» не является высказыванием, т. к. оно может быть истинным при некоторых значениях Х и Y и ложным при других значениях. Из простых, атомарных высказываний можно сооружать сложные высказывания. Например, из двух высказываний: «Москва стоит на берегу Невы» и «Санкт-Петербург стоит на берегу Невы», из которых первое ложно, второе истинно, можно соорудить более сложные высказывания: «Москва стоит на берегу Невы или Санкт-Петербург стоит на берегу Невы» (истинное) или «Москва стоит на берегу Невы и Санкт-Петербург стоит на берегу Невы» (ложное).

В логике высказываний простые высказывания являются булевыми переменными, принимающими значения «истина» (и) или «ложь» (л). Переменной (и) соответствует 1, переменной (л) – 0. Для них стандартным образом определяются булевы функции: дизъюнкция высказываний, конъюнкция (два последних примера), отрицание, эквивалентность, сумма по Mod 2 (исключающее «или»), импликация.

Рассмотрим более подробно последнюю функцию , где P и Q – высказывания, т. е. утверждение типа: « влечет » или «из следует », например, «Если 2х2=5, то Москва – столица». Не математик найдет это выражение ложным, ибо ему кажется, что в выражении « влечет » должно по смыслу вытекать из , только в этом случае утверждение истинно. Но тогда получается, что логическая связка « » зависит от смысла высказываний. Математики импликацию определяют стандартной таблицей истинности, которая не противоречит «здравому смыслу»: «л л» и «л и» – эти утверждения истинны, так как из ложной посылки можно получить как ложное, так и истинное утверждение. «и и» – истинное утверждение, так как из верной посылки с помощью верных рассуждений можно получить только истинное утверждение. «и л» – ложное утверждение, ибо из истинного утверждения с помощью верных рассуждений мы не сможем прийти к ложному результату.

Простые высказывания (булевы переменные) будем обозначать буквами , если понадобится, с индексами. Булевы функции от этих высказываний – . В логике высказываний можно ввести стандартное для функций алгебры логики понятие формулы. Формулы будем обозначать буквами латинского алфавита где в скобках перечислены входящие в формулу булевы переменные.

Формула называется Тавтологией, если она принимает значение 1 для любого набора значений входящих в нее переменных, т. е. если она реализует функцию константа 1.

Формула называется Противоречием, если она принимает значение 0 на всех наборах значений переменных (реализует функцию константа 0).

Формула называется Опровержимой, если существует набор значений , такой что

Формула называется Выполнимой, если существует набор значений , такой что

С точки зрения логики тавтология – логический закон, так как при любой подстановке вместо переменных конкретных высказываний мы получаем истинное высказывание. Перечислим наиболее важные тавтологии (А, В, С – произвольные формулы):

т. е. Эта тавтология называется Законом исключенного третьего или Tertium Nondatur.

– Цепное рассуждение.

– Закон ПиРса.

Любую из этих тавтологий можно обосновать, составив таблицу истинности и показав, что соответствующая функция есть константа. К этому же результату можно прийти с помощью эквивалентных преобразований.

Докажем, что – тавтология.

При доказательстве различных утверждений мы пользуемся «рассуждениями».

Рассуждение называется правильным, если из конъюнкции посылок следует заключение D, это записывается: , т. е. всякий раз, когда все посылки истинны, то заключение тоже истинно. Таким образом, чтобы установить правильность рассуждений, надо показать, что формула является тавтологией. Действительно, если какая-то из посылок ложна, то и импликация принимает значение 1. Если все посылки истинны и рассуждения верны, то заключение тоже должно быть верно и импликация вновь принимает значение 1.

Пример 1. Рассмотрим следующее «рассуждение»: «Если число 5 – простое, то оно нечетное. Число 5 – нечетное, следовательно, оно простое». Число 5 действительно простое, но сами рассуждения неверны. Введем обозначения для высказываний: Х – «5 – число простое», y – «5 – число нечетное». Тогда посылками будут заключением будет х. Рассуждения шли по схеме Строим формулу для определения правильности рассуждения: Проверим,

На наборе Х = 0, Y = 1 формула принимает значение 0, следовательно, она не является тавтологией. Эта формула будет тавтологией, если Х = Y, т. е. простое число и нечетное число – эквивалентные понятия. «Здравый смысл подсказывает», что в этом случае, действительно, рассуждения верны.

Пример 2. Если Петр занимается спортом, то Петр никогда не болеет. Петр занимается спортом, следовательно, он не болеет.

Введем обозначения для высказываний: X – «Петр занимается спортом», Y – «Петр не болеет».

Схема рассуждений Проверим правильность этой схемы рассуждений:

Распространенные схемы Правильных рассуждений: и . Правильность первой схемы доказана в примере 2. Докажем правильность второй схемы:

Рассмотрим высказывание вида где А – конъюнкция посылок, В – заключение. Если формула А – тавтология и рассуждения логически правильны, то заключение В принимает значение «истина», что следует из таблицы истинности для импликации. Такие Методы доказательства истинности заключения называются Прямыми. Иногда удобнее доказать истинность другого высказывания, эквивалентного данному. Такие формы доказательства называются Косвенными. Одним из них является метод Доказательства от противного.

1. Предполагаем, что высказывание ложно и приходим к противоречию, получаем, что истинными являются два высказывания: и , т. е. Применимость этой формы доказательства оправдывается следующей эквивалентностью:

2. Существуют и другие схемы доказательства от противного. Предполагаем, что из следует и приходим к тому, что истинными оказываются и или и . Эти схемы основаны на эквивалентности или .

Действительно, и

Другой метод косвенного доказательства – доказательство по Закону Контрапозиции, Когда вместо истинности мы доказываем истинность . Действительно,

Рассмотрим на конкретных задачах применение исчисления высказываний.

Пример 3. Записать составное высказывание в виде формулы, употребляя булевы переменные для обозначения простых высказываний.

А) если идет дождь, то дует ветер и становится холодно;

Б) если дует ветер, идет дождь;

В) ветер дует тогда и только тогда, когда идет дождь;

Г) неверно, что ветер дует тогда и только тогда, когда нет дождя.

Решение. Введем обозначения: Х – «идет дождь», У – «дует ветер», Z –«становится холодно».

Тогда приведенные высказывания можно записать в виде следующих формул: а) б) в) г) .

Пример 4. Выяснить, являются ли следующие рассуждения логически верными.

Если Джонс не встречал ночью Смита, то Смит был убийцей или Джонс лжет. Если Смит не был убийцей, то Джонс не встречал Смита этой ночью, и убийство имело место после полуночи. Если убийство имело место после полуночи, то Смит был убийцей или Джонс не лжет. Следовательно, Смит был убийцей.

Решение. Введем логические переменные: Х – «Джонс не встречал ночью Смита», У – «Смит убийца», Z – «Джонс лжет», T – «убийство состоялось после полуночи». Прежде чем записать формулу, надо уточнить по условию задачи в каком контексте употребляется союз «или». Когда мы говорим «А или В», мы можем подразумевать две разные ситуации: а) или б) Во втором случае высказывания А и В не могут быть одновременно истинными. Чтобы подчеркнуть этот момент, обычно говорят «либо А, либо В». В нашей задаче нет такой оговорки, поэтому мы можем для записи высказывания: «Смит был убийцей или Джонс не лжет» использовать формулу . Итак, мы имеем посылки: , , заключение: У. Надо составить формулу:

и посмотреть, будет ли она тавтологией:

Следовательно, рассуждения логически правильны.

Пример 5. Проверить совместность утверждений.

Здесь употреблено выражение «либо. либо. », поэтому первое составное высказывание следует записать в виде что эквивалентно Конъюнкция посылок имеет вид:

Это не равно тождественному 0, следовательно, высказывания не являются противоречивыми.

Пример 6. Четыре ученицы: Маша (М), Нина (Н), Ольга (О) и Поля (П) участвовали в соревнованиях и заняли первые 4 места. На вопрос, кто какое место занял, было дано 3 ответа:

О – второе, П – третье;

О – первое, Н – второе;

М – второе, П – четвертое.

В каждом из этих ответов одна часть верна, а другая нет. Какое место заняла каждая девушка?

Решение. Введем булевы переменные: Х – «О – второе», У – «П – третье», Z – «О – первое», T – «Н – второе», U – «М – второе», N – «П – четвертое». Получим систему уравнений: так как если X истинно, тогда Y ложно, а – истинно и либо Аналогично, Удобнее записать эту систему следующим образом:

Отсюда или окончательно,

Кроме того, так как одна ученица не может занять 2 места и одно место не может быть занято двумя ученицами. В результате в последнем уравнении останется единственный ненулевой член Отсюда или О – первая, М – вторая, П – третья, Н – четвертая.

Пример 7. Во время перемены в классе были Аня, Борис, Ваня и Майя. Один из них разбил окно. На вопрос:”Кто разбил окно?”, были даны ответы:

Аня: 1) Я не разбивала. 2) Я сидела и читала. 3) Майя знает, кто разбил.

Борис: 1) Я этого не делал. 2) С Майей я давно не разговариваю. 3) Это сделал Ваня.

Ваня: 1) Я не виновен. 2) Разбила Майя. 3) Борис лжёт, говоря, что разбил я.

Майя: 1) Я не разбивала. 2) Это вина Ани. 3) Борис знает, что я не виновна, т. е. мы с ним беседовали во время перемены.

Затем каждый признался, что из трёх ответов каждого, два – истинны, а один ложный. Кто разбил окно?

Решение. Введем булевы переменные. Высказывания, принадлежащие Ане, обозначим буквами с индексами ; высказывания, принадлежащие Борису – соответственно, принадлежащие Ване – и принадлежащие Майе – .

Запишем все формулы, которые являются тавтологиями, получим уравнения:

;

;

;

.

Выпишем все противоречия:

Чтобы иметь возможность воспользоваться этими противоречиями, возьмём конъюнкцию двух тавтологий:

и

Что тоже будет тавтологией. Получим

В этой формуле слева останется всего три ненулевых члена:

или Последнее уравнение даёт Так как и то и следовательно, а Следовательно, окно разбила Аня.

Рассмотрим еще одну задачу, для решения которой не требуется аппарат логики высказываний, но тем не менее эта задача относится к логическим задачам.

Пример 8. В кафе встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. «Замечательно, что один из нас имеет белые, один черные, а один рыжие волосы, но ни у кого цвет волос не совпадает с фамилией», – заметил черноволосый. «Ты прав», – сказал Белов. Какой цвет волос у художника?

Источник