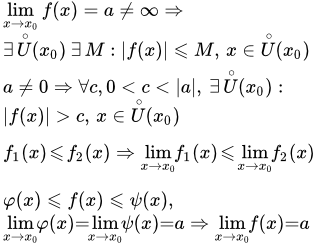Доказать по определению что предел равен

Предел последовательности

п.1. Определение последовательности

С понятием «последовательность» мы уже познакомились, когда изучали прогрессии (см. §24 справочника для 9 класса). По определению:

Т.е., числовая последовательность – это некий набор чисел с присвоенными им порядковыми номерами. Это набор можно задать формулой, описанием или просто перечислением.

Например:
1) Формула \(y_n=\frac1n,\ n\in\mathbb\) задает бесконечную последовательность дробей:

2) Формула \(y_n=(-1)^n,\ n\in\mathbb\) задает бесконечную последовательность «прыгающих» единиц:

3) Рекуррентная формула \(y_1=1,\ y_2=1,\ y_(n+2)=y_(n+1)+y_n\) задает бесконечную последовательность чисел Фибоначчи:

4) Описание «число π точностью до \(10^<-n>\)» задает бесконечную последовательность все более «подробных» значений числа π:

Этот ряд можно также задать формулой \(y_n=\frac<[\pi\cdot 10^n]><10^n>\), где квадратные скобки обозначают целую часть от числа.

п.2. Предел последовательности

Поведение последовательности «на длинных дистанциях» может быть неочевидным. Чтобы лучше понять, возрастает или убывает заданный ряд чисел, ограничен ли он какой-либо величиной или уходит на бесконечность, проще всего построить график.

1) \(y_n=\frac1n\) Последовательность сходится к 0

2) \(y_n=(-1)^n\) Последовательность ни к чему не сходится

3) числа Фибоначчи \(y_1=1,\ y_2=1,\ y_=y_+y_n\) Последовательность уходит на бесконечность

4) приближения числа π Последовательность сходится к π

п.3. Как доказать сходимость последовательности к пределу?

И построим график (в логарифмическом масштабе):

Мы видим, что чем меньше ε, тем больше \(N_<\varepsilon>\). Но главное – мы всегда можем его указать.
Таким образом, мы доказали, что действительно \(\lim_\frac<1>=0\)
Ведь для любого сколь угодно малого \(\varepsilon\gt 0\) мы можем указать такой номер \(N_<\varepsilon>=\left[\frac1\varepsilon-4\right]+1\), начиная с которого, для всех членов последовательности с номерами \(n\geq N_<\varepsilon>\) разность \(\left|\frac<1>-0\right|\), т.е. эти члены не выйдут за переделы ε окрестности предела b=0.

Построенный график интересен еще и тем, что показывает одно из важных практических применений логарифмов: если разбросы по шкалам очень велики, отличаются на порядки, то графики удобней строить в десятичных логарифмах.
Такие графики часто можно увидеть у физиков-ядерщиков, копающих вглубь, от нанометров до планковских длин; или у астрономов, всматривающихся вдаль, от тысяч километров до гигапарсек.

п.4. Ограниченные и неограниченные последовательности

п.5. Как доказать неограниченность последовательности?

Таким образом, мы доказали, что действительно \(\lim_n^2=+\infty\)
Ведь для любого сколь угодно большого \(M\gt 0\) мы можем указать такой номер \(N_M=[\sqrt]\), начиная с которого, для всех членов последовательности с номерами \(n\geq N_M,\ y_n=n^2\gt M\), т.е. члены последовательности становятся ещё больше.

п.6. Примеры

Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности \(N_<\varepsilon>=\left[\frac12\left(\frac<5><2\varepsilon>+3\right)\right]+1\), начиная с которого
\(\left|\frac<3-2n>+\frac12\right|\lt\varepsilon,\ n\geq N_<\varepsilon>\geq 2\).
Что и требовалось доказать.

Показанный приём с усилением неравенства часто применяется в математическом анализе. Найденное \(N_<\varepsilon>\) немного больше «точного» значения, которое следует из исходной дроби \(\frac<3(3n^2+n+1)>\), но наша задача в том, чтобы обоснованно построить любое выражение для стартового номера \(N_<\varepsilon>\) в зависимости от ε.
Если найденный номер будет немного больше исходного – не страшно; главное, чтобы он 1) был обоснован; 2) гарантировал размещение всех последующих \(y_n,\ n\geq N_<\varepsilon>\) в ε окрестности предела b.

Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности \(N_<\varepsilon>=\left[\frac<1><3\sqrt<\varepsilon>>\right]\), начиная с которого \(\left|\frac<3n^2+n+1>-\frac13\right|\lt\varepsilon,\ n\geq N_<\varepsilon>\geq 3\).
Что и требовалось доказать.

Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности \(N_<\varepsilon>=\left[-\log_3\varepsilon\right]\), начиная с которого \(\left|\frac<3^n+1><3^n>-1\right|\lt\varepsilon,\ n\geq N_<\varepsilon>\).
Что и требовалось доказать.

Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности \(N_<\varepsilon>=\left[\left(\frac<1><5\varepsilon>-1\right)^2\right]\), начиная с которого \(\left|\frac<\sqrt><5\sqrt+1>-\frac15\right|\lt\varepsilon,\ n\geq N_<\varepsilon>\).
Что и требовалось доказать.

Пример 2. Используя определения неограниченной последовательности, докажите, что:
a) \( \lim_2^n=+\infty \)
По условию: \(y_n=2^n\)
Записываем неравенство \(|y_n|\gt M\):
\begin 2^n\gt M\Rightarrow n\gt \log_2M\\ N_M=\left[\log_2M\right]+1 \end Например:

Таким образом, для любого сколь угодно большого \(M\gt 0\) мы можем указать такой номер \(N_M=\left[\log_2M\right]+1\), начиная с которого, для всех членов последовательности с номерами \(n\geq N_M,\ y_n=2^n\gt M\).
Что и требовалось доказать.

Таким образом, для любого сколь угодно большого \(M\gt 0\) мы можем указать такой номер \(N_M=\left[M^2\right]\), начиная с которого, для всех членов последовательности с номерами \(n\geq N_M,\ y_n=\sqrt\gt M\).
Что и требовалось доказать.

Источник

Пределы в математике для чайников: объяснение, теория, примеры решений

Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.

В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Понятие предела в математике

Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.

Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.

Звучит громоздко, но записывается очень просто:

Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.

В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.

Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Еще один вид неопределенностей: 0/0

В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:

Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

Сократим и получим:

Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.

Наглядно правило Лопиталя выглядит так:

Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.

А теперь – реальный пример:

Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.

Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Основные свойства предела функции

Формулировки свойств

Влияние значений функции в конечном числе точек на величину предела

Теорема об ограниченности функции, имеющей конечный предел

Теорема об ограниченности снизу функции, имеющей ненулевой предел

Теорема о пределе постоянной функции

Теорема об односторонних пределах

Функция имеет предел в точке тогда и только тогда, когда она имеет в этой точке равные односторонние пределы.
Доказательство ⇓

Свойство пределов функций, связанных неравенством

Свойство неравенств бесконечно больших функций

Теорема о промежуточной функции

Теорема о функциях, пределы которых связаны неравенством

Доказательство свойств

Влияние значений функции в конечном числе точек на величину предела

Теорема об ограниченности функции, имеющей конечный предел

Теорема об ограниченности снизу функции, имеющей ненулевой предел

Теорема о пределе постоянной функции

Теорема об односторонних пределах

Все свойства ⇑ Функция имеет предел в точке тогда и только тогда, когда она имеет в этой точке равные односторонние пределы.

Свойство пределов функций, связанных неравенством

Теорема о функциях, пределы которых связаны неравенством

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Предел функции

Понятие предела.

Важную роль в курсе математического анализа играет понятие предела, связанное с поведением функции в окрестности данной точки. Напомним, что \(\delta\) — окрестностью точки \(a\) называется интервал длины \(2\delta\) с центром в точке \(a\), то есть множество
$$
U_<\delta>(a)=\

Исследуем функцию \(f(x)=\displaystyle \frac\) в окрестности точки \(x=1\).

\(\triangle\) Функция \(f\) определена при всех \(x\in\mathbb\), кроме \(x=1\), причем \(f(x)=x+1\) при \(x\neq 1\). График этой функции изображен на рис. 10.1.

Рис. 10.1

Из этого рисунка видно, что значения функции близки к 2, если значения \(x\) близки к 1 (\(x\neq 1)\). Придадим этому утверждению точный смысл.

Пусть задано любое число \(\varepsilon>0\) и требуется найти число \(\delta>0\) такое, что для всех \(x\) из проколотой \(\delta\)-окрестности точки \(x=1\) значения функции \(f(x)\) отличаются от числа 2 по абсолютной величине меньше, чем на \(\varepsilon\).

Иначе говоря, нужно найти число \(\delta>0\) такое, чтобы для всех \(x\in\dot_<\delta>(a)\) соответствующие точки графика функции \(y=f(x)\) лежали в горизонтальной полосе, ограниченной прямыми \(y=2-\varepsilon\) и \(y=2+\varepsilon\) (см. рис. 10.1), то есть чтобы выполнялось условие \(f(x)\in U_<\varepsilon>(2)\). В данном примере можно взять \(\delta=\varepsilon\).

В этом случае говорят, что функция \(f(x)\) стремится к двум при \(x\), стремящемся к единице, а число 2 называют пределом функции \(f(x)\) при \(x\rightarrow 1\) и пишут \(\displaystyle \limf(x)=2\) или \(f(x)\rightarrow 2\) при \(x\rightarrow 1.\quad\blacktriangle\)

\(\triangle\) Из графика этой функции (рис. 10.2) видно, что для любого \(\varepsilon>0\) можно найти \(\delta>0\) такое, что для всех \(x\in\dot_<\delta>(0)\) выполняется условие \(f(x)\in U_<\varepsilon>(1)\). В самом деле, прямые \(y=1+\varepsilon\) и \(y=1-\varepsilon\) пересекают график функции \(y=f(x)\) в точках, абсциссы которых равны \(x_<1>=-\varepsilon,\ x_2=\sqrt<\varepsilon>\). Пусть \(\delta\) — наименьшее из чисел \(|x_<1>|\) и \(x_2\), т.e. \(\displaystyle \delta=\min(\varepsilon,\sqrt<\varepsilon>)\). Тогда если \(|x|

Два определения предела функции и их эквивалентность.

Определение предела по Коши.

Число \(A\) называется пределом функции \(f(x)\) в точке \(a\), если эта функция определена в некоторой окрестности точки \(a\), за исключением, быть может, самой точки \(a\), и для каждого \(\varepsilon>0\) найдется число \(\delta>0\) такое, что для всех \(x\), удовлетворяющих условию \(|x-a| 0\ \exists\delta>0:\ \forall x:0 0\ \exists\delta>0:\ \forall x\in\dot_<\delta>(a)\rightarrow f(x)\in U_<\varepsilon>(A).\nonumber
$$

Таким образом, число \(A\) есть предел функции \(f(x)\) в точке \(a\), если для любой \(\varepsilon\)-окрестности числа \(A\) можно найти такую проколотую \(\delta\)-окрестность точки \(a\), что для всех \(x\), принадлежащих этой \(\delta\)-окрестности, соответствующие значения функции содержатся в \(\varepsilon\)-окрестности числа \(A\).

В определении предела функции в точке \(a\) предполагается, что \(x\neq a\). Это требование связано с тем, что точка \(a\) может не принадлежать области определения функции. Отсутствие этого требования сделало бы невозможным использование предела для определения производной, так как производная функции \(f(x)\) в точке \(a\) — это предел функции
$$
F(x) = \frac,\nonumber
$$
которая не определена в точке \(a\).

Отметим еще, что число \(\delta\), фигурирующее в определении предела, зависит, вообще говоря, от \(\varepsilon\), то есть \(\delta=\delta(\varepsilon)\).

Определение предела по Гейне.

Число \(A\) называется пределом функции \(f(x)\) в точке \(a\), если эта функция определена в некоторой проколотой окрестности точки \(\alpha\), то есть \(\exists\delta_<0>>0:\ \dot_<\delta_<0>>(a)\subset D(f)\), и для любой последовательности \(\\>\), сходящейся к \(a\) и такой, что \(x_\in U_<\delta_0>(a)\) для всех \(n\in\mathbb\), соответствующая последовательность значений функции \(\)\>\) сходится к числу \(A\).

Пользуясь определением предела по Гейне, доказать, что функция

$$
f(x)=\sin\frac<1>\nonumber
$$
не имеет предела в точке \(x=0\).

\(\triangle\) Достаточно показать, что существуют последовательности \(\\>\) и \(\<\widetilde_\>\) с отличными от нуля членами, сходящиеся к нулю и такие, что \(\displaystyle \lim_f(x_)\neq\lim_ f(\widetilde_n)\).

Тогда \(\displaystyle \lim_x_=\lim_\widetilde_=0,\ f(x_)=1\) и \(f(\widetilde_)=0\) для всех \(n\in\mathbb\) и поэтому \(\displaystyle \lim_f(x_)=1\), a \(\displaystyle \lim_f(\widetilde_)=0\). Следовательно, функция \(\displaystyle \sin\frac<1>\) не имеет предела в точке \(x=0.\quad \blacktriangle\)

Если функция \(f\) определена в проколотой \(\delta_<0>\)-окрестности точки \(a\) и существуют число \(A\) и последовательность \(\\) такие, что \(x_n \in \dot_<\delta_<0>>(a)\) при всех \(n \in\mathbb,\ \displaystyle \lim_x_=a\) и \(\displaystyle \lim_f(x_)=A\), то число \(A\) называют частичным пределом функции \(f\) в точке \(a\).

Так, например, для функции \(f(х)=\displaystyle \sin\frac<1>\) каждое число \(A \in [-1, 1]\) является ее частичным пределом. В самом деле, последовательность \(\\>\), где \(x_=\displaystyle (\arcsin A+2\pi n)^<-1>\), образованная из корней уравнения \(\displaystyle \sin\frac<1>=A\) (рис. 10.3), такова, что \(x_n\neq 0\) для всех \(n\in\mathbb,\ \displaystyle \lim_x_n=0\) и \(\displaystyle \lim_f(x_)=A\).

Рис. 10.3

Эквивалентность двух определений предела.

Определения предела функции по Коши и по Гейне эквиваленты.

\(\circ\) В определениях предела функции \(f(x)\) по Коши и по Гейне предполагается, что функция \(f\) определена в некоторой проколотой окрестности точки \(a\), то есть существует число \(\delta_0>0\) такое, что \(\dot_<\delta_<0>>\in D(f)\).

Пусть \(а\) — предельная точка числового множества \(E\), то есть такая точка, в любой окрестности которой содержится по крайней мере одна точка множества \(E\), отличная от \(a\). Тогда число \(A\) называют пределом по Коши функции \(f(x)\) в точке \(a\) по множеству \(E\) и обозначают \(\displaystyle \lim_f(x)=A\), если
$$
\forall\varepsilon>0\quad \exists\delta>0:\quad\forall x\in \dot_<\delta>(a)\cap E\rightarrow|f(x)-A|

Различные типы пределов.

Односторонние конечные пределы.

Число \(A\) называют пределом слева функции \(f(x)\) в точке a и обозначают \(\displaystyle \lim_>f(x)\) или \(f(a-0)\), если
$$
\forall\varepsilon>0\quad\exists\delta>0:\quad\forall x\in(a-\delta,a)\rightarrow|f(x)-A_<1>| 0\quad\exists\delta>0:\ \forall x\in (a,a+\delta)\rightarrow|f(x)-A_2| 0,
\end\right.\nonumber
$$
график которой изображен на рис. 10.4 \(\displaystyle \lim_f(x)=f(-0)=-1,\ \displaystyle \lim_f(x)=f(+0)=1\).

Рис. 10.4

Отметим еще, что если
$$
\forall\varepsilon>0\ \exists\delta>0:\forall x\in\dot_<\delta>(a)\rightarrow f(x)\in[A,A+\varepsilon),
$$
то есть значения функции лежат в правой \(\varepsilon\)-полуокрестности числа \(A\), то пишут \(\displaystyle \lim_f(x)=A+0\). В частности, если \(A=0\), то пишут \(\displaystyle \lim_f(x)=+0\).

Аналогично
$$
\displaystyle \<\lim_f(x)=A-0\>\Leftrightarrow\forall\varepsilon>0\ \exists\delta>0:\ \forall x\in\dot_<\delta>(a)\rightarrow f(x)\in (A-\varepsilon,A\rbrack.\nonumber
$$
Например, для функции
$$
\varphi (x)=\left\<\begin
1-x,\ если\ x 0,
\end\right.\nonumber
$$
график которой изображен на рис. 10.5, \(\displaystyle \lim_f(x)=1+0\).

Рис. 10.5

Аналогичный смысл имеют записи вида
$$
\lim_f(x)=A+0,\quad \lim_f(x)=A-0\nonumber
$$

Например,
$$
\displaystyle \<\lim_f(x)=A+0\>\Leftrightarrow\forall\varepsilon>0\exists\delta>0:\forall x\in(a-\delta,a)\rightarrow f(x)\in[A,A+\varepsilon).
$$

Бесконечные пределы в конечной точке.

Говорят, что функция \(f(x)\), определенная в некоторой проколотой окрестности точки \(a\), имеет в этой точке бесконечный предел, и пишут \(\lim_f(x)=\infty\), если
$$
\forall\varepsilon>0\quad\exists\delta>0:\ \forall x\in\dot_<\delta>(a)\rightarrow|f(x)|>\varepsilon.\label
$$

В этом случае функцию \(f(x)\) называют бесконечно большой при \(x\rightarrow a\).

Рис. 10.6

Например, если \(f(x)=1/x\), то \(\displaystyle \lim_f(x)=\infty\), так как условие \eqref выполняется при \(\delta=1/\varepsilon\) (рис.10.6).

Аналогично говорят, что функция \(f(x)\), определенная в некоторой проколотой окрестности точки \(a\), имеет в этой точке предел, равный \(+\infty\), и пишут \(\displaystyle \lim_f(x)=+\infty\), если \(\forall\varepsilon>0\quad\exists\delta>0:\ \forall x\in\dot_<\delta>(a)\rightarrow f(x)>\varepsilon\), то есть \(f(x)\in U_<\varepsilon>(+\infty)\), где множество \(U_\varepsilon (+\infty )\) называют \(\varepsilon\)-окрестностью символа \(+\infty\).

Если
$$
\forall\varepsilon>0\quad\exists\delta>0:\forall x\in\dot_<\delta>(a)\rightarrow f(x) Рис. 10.7 Рис. 10.8

Предел в бесконечности.

$$
\forall\varepsilon>0\exists\delta>0:\forall x\in U_<\delta>(+\infty)\rightarrow f(x)\in U_<\varepsilon>(A),\nonumber
$$

то говорят, что число \(A\) есть предел функции \(f(x)\) при x, стремящемся к плюс бесконечности, и пишут \(\displaystyle \lim_ f(x)=A.\)

Например, если \(f(x)=\displaystyle\frac<3-2x>\), то \(\displaystyle \lim_ f(x)=-2\). В самом деле \(f(x)=-2+\frac<5>\), и если \(x>0\), то \(x+1>x>0.\) Поэтому \(\displaystyle\frac<5> 0\) выполняется при любом \(x >\delta\), где \(\delta=\displaystyle\frac<5><\varepsilon>\), то есть при любом \(x\in U_<\delta>(+\infty)\).

Если \(\forall\varepsilon>0 \ \exists\delta>0:\forall x\in U_<\delta>(-\infty)\rightarrow f(x)\in U_<\varepsilon>(A)\), то есть неравенство \(|f(x)-A| 0\ \exists\delta>0:\forall x\in U_<\delta>(\infty)\rightarrow f(x)\in U_<\varepsilon>(A),\nonumber
$$
то говорят, что число A есть предел функции f(x) при x, стремящемся к бесконечности, и пишут \(\displaystyle \lim_=A\). Например, если \(f(x)=\frac<3-2x>\), то \(\displaystyle \lim_f(x)=-2.\)

Точно так же вводится понятие бесконечного предела в бесконечности. Например,запись \(\displaystyle \lim_ f(x)=-\infty\) означает, что
$$
\forall\varepsilon>0\ \exists\delta>0:\forall x\in U_<\delta>(+\infty)\rightarrow f(x)\in U_<\varepsilon>(-\infty).\nonumber
$$
Аналогично определяются бесконечные пределы при \(x\rightarrow\infty\) и \(x\rightarrow-\infty.\)

Свойства пределов функций.

Локальные свойства функции, имеющей предел.

Покажем, что функция, имеющая конечный предел в заданной точке, обладает некоторыми локальными свойствами, то есть свойствами, которые справедливы в окрестности этой точки.

Если функция \(f(x)\) имеет предел в точке \(a\), то существует такая проколотая окрестность точки \(a\), в которой эта функция ограничена.

\(\circ\) Пусть \(\displaystyle \lim_f(x)=A\). В силу определения предела по заданному числу \(\varepsilon=1\) можно найти число \(\delta>0\) такое, что для всех \(x\in\dot_<\delta>(a)\) выполняется неравенство \(|f(x)-A| Свойство 2

Свойство сохранения знака предела.

Если \(\displaystyle \lim_f(x)=A\), причем \(A\neq 0,\) то найдется такая проколотая окрестность точки \(a\), в которой значения функции \(f\) имеют тот же знак, что и число \(A\).

\(\circ\) Согласно определению предела по заданному числу \(\varepsilon = \frac<|A|><2>>0\) можно найти такое число \(\delta>0\), что для всех \(x\in\dot_<\delta>(a)\) выполняется неравенство \(\displaystyle |f(x)-A| 0\), то из левого неравенства \eqref следует, что
$$
f(x)>\frac<2>>0\ для\ x\in\dot_<\delta>(a).\nonumber
$$
Если \(A Свойство 3

Если \(\displaystyle \lim_g(x)=B\), причем \( B\neq0\), то существует число \(\delta>0\) такое, что функция \(\displaystyle\frac<1>\) ограничена на множестве \(\dot_<\delta>(a).\)

\(\circ\) В силу определения предела по заданному числу \(\varepsilon=\frac<|B|><2>\) можно найти число \(\delta>0\), такое, что для всех \(x\in\dot_\delta(a)\) выполняется неравенство
$$
|g(x)-B| \frac<|B|><2>\),и поэтому \(\displaystyle \frac<1> <|g(x)|>Свойство 1

Если существует число \(\delta>0\) такое, что для всех \(\dot_<\delta>(a)\) выполняются неравенства
$$
g(x)\leq f(x)\leq h(x),\label
$$
и если
$$
\lim_g(x)=\lim_h(x)=A,\label
$$
то существует \(\displaystyle \lim_f(x)=A.\)

\(\circ\) Воспользуемся определением предела функции по Гейне. Пусть \(\\>\) — произвольная последовательность такая, что \(x_n\in\dot_<\delta>(a)\) для \(n\in\mathbb\) и \(\displaystyle \lim_f(x)=a\). Тогда в силу условия \eqref \(\displaystyle \lim_g(x_)=\lim_h(x_)=A.\)

Так как, согласно условию \eqref, для всех \(n\in\mathbb\) выполняется неравенство
$$
g(x_)\leq f(x_)\leq h(x_),\nonumber
$$
то в силу свойств пределов последовательностей \(\displaystyle \lim_f(x_)=A\). Следовательно, \(\displaystyle \lim_f(x)=A.\ \bullet\)

\(\circ\) Для доказательства этого свойства достаточно воспользоваться определением предела функции по Гейне и соответствующими свойствами пределов последовательностей. \(\bullet\)

Бесконечно малые функции обладают следующими свойствами:

Эти свойства легко доказать, используя определения бесконечно малой и ограниченной функции, либо с помощью определения предела функции по Гейне и свойств бесконечно малых последовательностей. Из свойства 2) следует, что произведение конечного числа бесконечно малых при \(x\rightarrow a\) функций есть бесконечно малая при \(x\rightarrow a\) функция.

Из определения предела функции и определения бесконечно малой функции следует, что число \(A\) является пределом функции \(f(x)\) в точке \(a\) тогда и только тогда, когда эта функция представляется в виде
$$
f(x)=A+a(x),\nonumber
$$ где \(a(x)\) — бесконечно малая при \(x\rightarrow a\) функция.

Свойства пределов, связанные с арифметическими операциями.

Если функции \(f(x)\) и \(g(x)\) имеют конечные пределы в точке \(а\), причем \(\displaystyle \lim_f(x)=A,\ \lim_g(x)=B\), то:

\(\circ\) Для доказательства этих свойств достаточно воспользоваться определением предела функции по Гейне и свойствами пределов последовательностей. \(\bullet\)

Отметим частный случай утверждения \eqref:
$$
\lim_(C f(x))=C\lim_f(x),\nonumber
$$
то есть постоянный множитель можно вынести за знак предела.

Пределы монотонных функций.

Ранее мы уже ввели понятие монотонной функции. Докажем теорему о существовании односторонних пределов у монотонной функции.

Если функция \(f\) определена и является монотонной на отрезке \([a,b]\), то в каждой точке \(x_<0>\in(a,b)\) эта функция имеет конечные пределы слева и справа, a в точках \(а\) и \(b\) — соответственно правый и левый пределы.

\(\circ\) Пусть, например, функция \(f\) является возрастающей на отрезке \([a,b]\). Зафиксируем точку \(х_0\in\)(а, \(b\)]. Тогда
$$
\forall x\in[a,x_<0>)\rightarrow f(x)\leq f(x_<0>).\label
$$

В силу условия \eqref множество значений, которые функция \(f\) принимает на промежутке \([a,x_<0>)\), ограничено сверху, и по теореме о точной верхней грани существует
$$
\sup_\in[a,\ x_<0>):M-\varepsilon 0\), так как \(x_\varepsilon 0\ \exists\delta>0:\forall x\in(x_<0>-\delta,x_<0>)\rightarrow f(x)\in(M-\varepsilon,M].\nonumber
$$
Согласно определению предела слева это означает, что существует
$$
\lim_-0> f(x)=f(x_<0>-0)=M.\nonumber
$$
Итак,
$$
f(x_<0>-0)=\sup_

Если функция \(f\) определена и возрастает на отрезке \([a,b],\ x_<0>\in(a,b),\) то
$$
f(x_<0>-0) Замечание.

Теорема о пределе монотонной функции справедлива для любого конечного или бесконечного промежутка. При этом, если \(f\) — возрастающая функция, не ограниченная сверху на \((a,b)\), то \(\displaystyle \lim_f(x)= +\infty\) (в случае, когда \(b =+\infty\) пишут \(\displaystyle \lim_f(x)= +\infty\)), а если \(f\) — возрастающая и не ограниченная снизу на промежутке \((a,b)\) функция, то \(\displaystyle \lim_f(x)=-\infty\quad (\lim_f(x)=-\infty)\).

Критерий Коши существования предела функции.

Будем говорить, что функция \(f(x)\) удовлетворяет в точке \(x=a\) условию Коши, если она определена в некоторой проколотой окрестности точки \(a\) и
$$
\forall\varepsilon>0\quad \exists\delta=\delta(\varepsilon)>0:\ \forall x’,x″\in \dot_<\delta>(a)\rightarrow|f(x’)-f(x″)|

Пусть существует число \(\delta >0\) такое, что функция \(f(x)\) определена в проколотой \(\delta\) — окрестности точки \(a\), и пусть для каждой последовательности <\(x_n\)>, удовлетворяющей условию \(x_n\in\dot_<\delta>(a)\) при всех \(n\in\mathbb\) и сходящейся к \(a\), соответствующая последовательность значений функции \(\) имеет конечный предел. Тогда этот предел не зависит от выбора последовательности \(\), то есть если
$$
\lim_f(x_)=A,\nonumber
$$
и
$$
\lim_f(\widetilde>)=\widetilde,\nonumber
$$
где \(\widetilde_n =\dot_<\delta>(a)\) при всех \(n \in\mathbb\) и \( \widetilde_\rightarrow a \) при \(n\rightarrow\infty\) то \(\widetilde=A.\)

\(\circ\) Образуем последовательность
$$
x_<1>,\widetilde_<1>, x_<2>,\widetilde_<2>,\ldots, x_,\widetilde_,\ldots\nonumber
$$
и обозначим k-й член этой последовательности через \(y_\). Так как \(\displaystyle \lim_y_k=a\) (см. пример 3 здесь) и \(y_k\in \dot_<\delta>(a)\) при любом \(k\in\mathbb\), то по условию леммы существует конечный \(\displaystyle \lim_f(y_)=A’\) Заметим, что \(\)\>\) и \(\_)\>\) являются подпоследовательностями сходящейся последовательности \(\\). Поэтому \(A=A’,\widetilde=A’\) откуда получаем, что \(A=\widetilde.\ \bullet\)

Для того чтобы существовал конечный предел функции \(f(x)\) в точке \(x = a\) необходимо и достаточно, чтобы эта функция удовлетворяла в точке a условию Коши \eqref.

\(\circ\) Необходимость. Пусть \(\displaystyle \lim_f(x)=A\); тогда
$$
\forall\varepsilon>0 \ \exists\delta>0:\forall x\in\dot_<\delta>(a)\rightarrow|f(x)-A| 0\) можно найти число \(\delta=\delta_\varepsilon>0\) такое, что
$$
\forall x’,x″\in \dot_<\delta>(a)\rightarrow|f(x’)-f(x″)| 0,\) указанное в условии \eqref, найдем в силу определения предела последовательности номер \(n_<\delta>=N_<\varepsilon>\) такой, что
$$
\forall n>N_<\varepsilon>\rightarrow 0 Замечание.

Теорема 3 остается в силе, если точку \(a\) заменить одним из символов \(a-0, a+0,-\infty, +\infty\); при этом условие \eqref должно выполняться в окрестности этого символа.

Источник