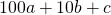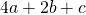Докажите что 1736907064 делится на 8
Признак делимости на 8, примеры, доказательство.
Навигация по странице.
Признак делимости на 8, примеры
Из приведенной формулировки признака делимости на 8 понятно, что этот признак применяется лишь для четырехзначных, пятизначных и так далее чисел (при необходимости смотрите многозначные натуральные числа), причем этот признак сводит проверку делимости данного числа к проверке делимости соответствующего трех, двух или однозначного числа. А чтобы установить делимость на 8 однозначных, двузначных и трехзначных чисел, можно выполнить деление этих чисел на 8 непосредственно.
Рассмотрим примеры применения признака делимости на 8.
Доказательство признака делимости на 8
Пусть a целое число, запись которого состоит из четырех, пяти или большего количества знаков. Модуль числа a – есть число натуральное, поэтому мы его можем представить в виде 
Другие случаи делимости на 8
Во-первых, к произведению иногда помогает прийти бином Ньютона. Покажем это на примере.
Представим 9 как 8+1 и воспользуемся формулой бинома Ньютона:
Разложим исходное выражение на множители: 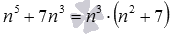
Еще при доказательстве делимости на 8 бывает полезным метод математической индукции. Разберем его применение на первом примере из этого пункта.
Признак делимости на 8

Всего получено оценок: 219.
Всего получено оценок: 219.
Признак делимости на 8 достаточно большой, в сравнении с другими признаками. Его тяжелее понять и запомнить, но 8 куда чаще других чисел используется в делении. Поэтому разберем правило во всех подробностях, чтобы проблем с делимостью больше не возникало.
Что такое признак делимости на 8
Числа, которые делятся на 8, подразделяются на 2 большие группы:
Признак делимости показывает, можно ли поделить одно число на другое без остатка.
Первая группа
Трехзначные числа можно представить в виде формулы авс, где а, в и с – цифры, с помощью которых записано число.
Трехзначное число делится на 8, если сумма: 4а+2в+с делится на 8.
Сумма: 5*4+9*2+7=20+18+7=35 – 35 на 8 не делится, значит и все число не делится на 8.
Нужно понимать, что цифры – это знаки, с помощью которых мы записываем числа. Именно числа отражают реальные величины в математике.
Вторая группа
У чисел больше тысячи рассматриваются последние три цифры. Если число из этих трех цифр делится на 8, то и все число делится на 8.
Такое трехзначное число называется гранью. Поэтому можно сформулировать признак так: Если первая трехзначная грань числа делится на 8, то и все число делится на 8
1254862245 – число делится на 8, если число 245 делится на 8. Это можно проверить с помощью признака первой группы.
2*4+4*2+5=8+8+5=21 – не делится на 8, значит и все большое число не делится на 8.
Что мы узнали?
Мы поговорили о признаке делимости на 8, выяснили к каким группам чисел и как применяется этот признак. Рассмотрели правило и примеры признака делимости на 8.
Признаки делимости чисел
В данной публикации мы рассмотрим признаки делимости на числа от 2 до 11, сопроводив их примерами для лучшего понимания.
Признак делимости – это алгоритм, используя который можно сравнительно быстро определить, является ли рассматриваемое число кратным заранее заданному (т.е. делится ли на него без остатка).
Признак делимости на 2
Число делится на 2 тогда и только тогда, когда его последняя цифра является четной, т.е. также делится на два.
Примеры:
Признак делимости на 3
Число делится на 3 тогда и только тогда, когда сумма всех его цифр, также, делится на три.
Примеры:
Признак делимости на 4
Двузначное число
Число делится на 4 тогда и только тогда, когда сумма удвоенной цифры в разряде его десятков и цифры в разряде единиц, также, делится на четыре.
Число разрядов больше 2
Число кратно 4, когда две его последние цифры образуют число, делящееся на четыре.
Примечание:
Число делится на 4 без остатка, если:
Признак делимости на 5
Число делится на 5 тогда и только тогда, когда его последняя цифра – это 0 или 5.
Примеры:
Признак делимости на 6
Число делится на 6 тогда и только тогда, когда он одновременно кратно и двум, и трем (см. признаки выше).
Примеры:
Признак делимости на 7
Число делится на 7 тогда и только тогда, когда сумма утроенного числа его десятков и цифры в разряде единиц, также, делится на семь.
Признак делимости на 8
Трехзначное число
Число делится на 8 тогда и только тогда, когда сумма цифры в разряде единиц, удвоенной цифры в разряде десятков и учетверенной в разряде сотен делится на восемь.
Число разрядов больше 3
Число делится на 8, когда три последние цифры образуют число, делящееся на 8.
Признак делимости на 9
Число делится на 9 тогда и только тогда, когда сумма всех его цифр, также, делится на девять.
Примеры:
Признак делимости на 10
Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль.
Примеры:
Признак делимости на 11
Число делится на 11 тогда и только тогда, когда модуль разности сумм четных и нечетных разрядов равен нулю или делится на одиннадцать.
Примеры:
Признак делимости на 8
Делимость нацело числа на 8 зависит от последних трёх цифр в его записи.
Признак делимости на 8
Натуральное число делится без остатка на 8,
— если его запись оканчивается тремя цифрами, образующими число, которое делится без остатка на 8;
— если его запись оканчивается тремя нулями.
Проверить делимость на 8 трёхзначного числа проще всего непосредственным делением. Но и в этом случае есть признак.
Признак делимости трёхзначного числа на 8
(то есть его запись состоит из цифр a, b и c соответственно) делится без остатка на 8, если
(к умноженному на 4 числу сотен прибавляем удвоенное число десятков и число единиц и проверяем делимость полученной суммы на 8).
1) Определить, какие из данных трёхзначных чисел делятся без остатка на 8:
Делимость этих чисел на 8 можно проверить непосредственным делением. Если же использовать признак делимости на 8 трёхзначного числа, получим:
4∙9+2∙5+2=48. Так как 48 делится на 8, то и 952 делится на 8.
4∙5+2∙2+8=32. 32 делится на 8, значит 528 также делится на 8.
4∙2+2∙3+6=20. Поскольку 20 не делится на 8, то и 236 не делится нацело на 8.
4∙7+2∙9+4=50. 50 не делится на 8, следовательно, 794 не делится без остатка на 8.
2) Какие из чисел делятся нацело на 8:
12320; 5246; 75000; 688975; 234984; 813758; 943552; 420783; 382268; 563000; 231608; 117376; 492170; 571824; 45657.
Прежде всего отбросим все нечётные числа:
688975, 420783, 45657 — они не делятся на 8 без остатка.
Выберем числа, запись которых оканчивается тремя нулями:
75000, 563000 — они делятся на 8.
В оставшихся числах проверяем делимость на 8 числа, образованного тремя последними цифрами:
12 320 делится на 8, так как 320 делится на 8 без остатка;
5 246 не делится на 8, так как 246 не делится на 8;
234 984 делится на 8, так как 984 кратно 8;
813 758 не делится на 8, поскольку 758 не делится на 8 без остатка;
943 552 делится на 8, потому что 552 делится на 8;
382 268 не делится на 8, так как 268 не делится на 8;
231 608 делится на 8, потому что 608 делится на 8;
117 376 делится на 8, так как 376 делится нацело на 8;
492 170 не делится на 8 без остатка, так как 170 не делится на 8;
571 824 делится на 8, потому что 824 кратно 8.
Ответ: 12320; 75000; 234984; 943552; 563000; 231608; 117376; 571824.
Признаки делимости чисел
Что такое «признак делимости»
Признак делимости числа — это такая особенность числа, которая еще до выполнения деления позволяет определить, кратно ли число делителю.
Истинный путь джедая, чтобы зря не пыхтеть над числами, которые в конечном итоге не делятся.
Однозначные, двузначные и трехзначные числа
Однозначное число — это такое число, в составе которого один знак (одна цифра). Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные числа — такие, в составе которых два знака (две цифры). Цифры могут повторяться или быть различными.
Трехзначные числа — числа, в составе которых три знака (три цифры).
Чётные и нечётные числа
Число называют четным тогда, когда оно делится на два без остатка. А нечетные числа — те, что на два без остатка не делятся. Все просто!
Признаки делимости чисел
Признак делимости на 2. Сразу можно сказать, что число делится на 2, если последняя цифра четная.
Признак делимости на 3. Сумма цифр числа должна делиться на 3.
Признаки делимости на 4. Число делится на 4, если две последние цифры — 0 или если они образуют цифру, которая делится на 4.
Признаки делимости на 5. Число делится на 5, если заканчивается на 0 или 5.
Признак делимости на 6. На 6 делятся те числа, которые могут одновременно делится на 2 и на 3.
Признаки делимости на 8. Число делится на 8, если три последних цифры — 0 или если они образуют число, которое делится на 8.
Признак делимости на 9. Число делится на 9, если сумма цифр делится на 9.
Признаки делимости на 10, 100. Числа, которые заканчиваются на 0, 00, 000 делятся на 10, 100, 1000 и так далее.