Докажите что биссектрисы углов параллелограмма образуют прямоугольник

Докажите, что биссектрисы углов произвольного параллелограмма при пересечении образуют прямоугольник?

Докажите, что биссектрисы углов произвольного параллелограмма при пересечении образуют прямоугольник.

Помогите, очень нужно &gt ; &lt ;

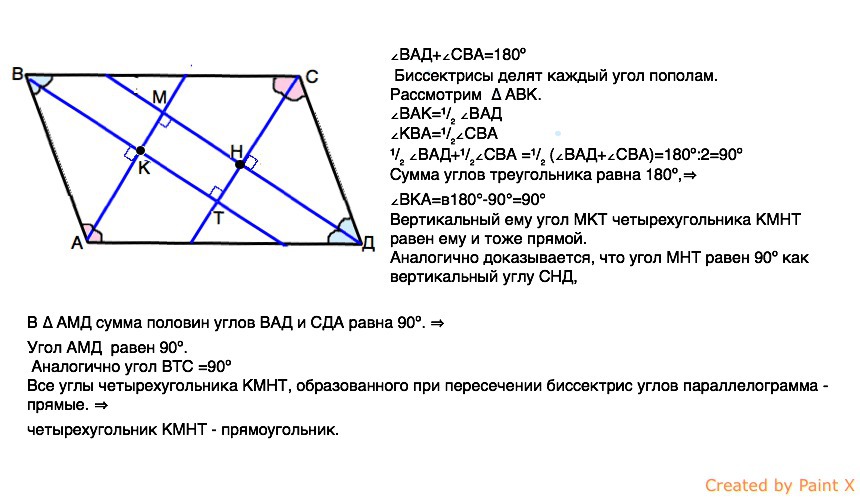
В параллелограмме противоположные углы равны по определению.

Так как противоположные стороны параллелограмма параллельны, то сумма его внутренних односторонних углов, как углов при параллельных прямых и секущей, равна 180º.

Биссектрисы параллелограммаделят каждыйего угол пополам.

¹ / ₂∠ВАД + ¹ / ₂∠СВА = ¹ / ₂ (∠ВАД + ∠СВА) = 180º : 2 = 90º

Сумма углов треугольника равна 180º, ⇒

Вертикальный ему угол МКТчетырехугольника КМНТ равен ему и тоже прямой.

Аналогично доказывается, что угол МНТ равен 90º как вертикальный углу СНД,

В ∆ АМД сумма половин внутренних одностороннихуглов ВАД и СДА равна 90º.

Угол АМД равен 90º.

Аналогично угол ВТС = 90º

Помогите пожалуйста решить, очень нужно.

Докажите что биссектрисы противоположных углов параллелограмма параллельны или совпадают?

Докажите что биссектрисы противоположных углов параллелограмма параллельны или совпадают.

Найдите угол при вершине этого треугольника.

Очень срочно нужно!

В параллелограмме, смежные стороны которого не равны, проведены биссектрисы углов?

В параллелограмме, смежные стороны которого не равны, проведены биссектрисы углов.

Докажите, что при их пересечении образуется прямоугольник.

Докажите, что биссектрисы острых углов прямоугольного треугольника при пересечении образуют угол 45 градусов?

Докажите, что биссектрисы острых углов прямоугольного треугольника при пересечении образуют угол 45 градусов.

Докажите, что биссектрисы двух соседних углов параллелограмм перпендикулярны?

Докажите, что биссектрисы двух соседних углов параллелограмм перпендикулярны.

В четырёхугольнике ABCD проведены биссектриса угла А и биссектриса угла В?

В четырёхугольнике ABCD проведены биссектриса угла А и биссектриса угла В.

Биссектриса угла А пересекает сторону ВС в точке М, а биссектриса угла В — сторону AD в точке N.

Известно, что MCDN — параллелограмм.

Докажите, что ABCD — параллелограмм.

В углах смежных с углами ромба проведены биссектрисы, доказать что при их пересечении образуется прямоугольник?

В углах смежных с углами ромба проведены биссектрисы, доказать что при их пересечении образуется прямоугольник.

Докажите, что параллелограмм является прямоугольником?

Докажите, что параллелограмм является прямоугольником.

Если диагонали образуют равные углы с одной из его сторон.

Составим систему 2x + 2y = 96 xy = 540 И решим ее Ответом будет пара чисел 18 и 30 или 25 и 23.

Думаю, из рисунка все ясно без лишних слов.

Прямая m принадлежит обеим плоскостям, все общие точки плоскостей альфа и бета принадлежат прямой m. Точка М одновременно принадлежит прямой а, плоскости альфа и плоскости бетта. Все общие точки плоскостей альфа и бетта принадлежат прямой m. Поэто..

1)АВD ABC 2)ABD BDC 3)ABE ECD.

А) 1 = 40 2 = 50 б) 1 = 65 2 = 65 в) 1 = 45 2 = 45.

Авиапочта, метеоусловия, полдома, пятидесятилетие, времяисчисление, горицвет, рособрннадзор, фотовыставка, мосжилстрой.

Источник