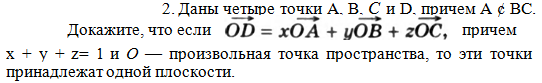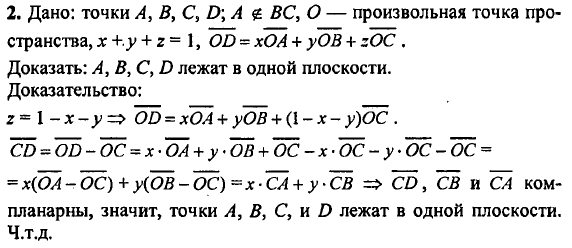Докажите что четыре точки

Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников

ГИА. Модуль Геометрия. Четыре точки лежат на одной окружности (1.10.2013)

В остроугольном треугольнике ABC угол B равен 60°. Докажите, что точки A, C, центр описанной окружности треугольника ABC и точка пересечения высот треугольника ABC лежат на одной окружности.

Автор: Ольга Себедаш Просмотров: 27699

Комментарии к этой задаче:

Комментарий добавил(а): светлана
Дата: 2013-10-25

конечно,красиво,но длинно, трудно и ученикам почти не доступно!

Комментарий добавил(а): Тамара Александровна Рыскина
Дата: 2013-10-09

Комментарий добавил(а): Елена
Дата: 2013-11-23

Опять развлекаются взрослые люди, а задача для кого?

Комментарий добавил(а): Ольга Себедаш
Дата: 2013-11-23

Елена, задача для думающих людей. Среди учеников таких много. Кто думать не хочет, за такие задачи и не берётся. Зачем?

Комментарий добавил(а): Татьяна Васильевна
Дата: 2013-11-21

Все понятно. Отлично!

Комментарий добавил(а): Майя
Дата: 2014-01-12

Комментарий добавил(а): Лексей
Дата: 2014-01-12

Эта задача из ГИА 9 класса. Это очень сложная задача для 9 класса. Кризис образования!

Комментарий добавил(а): Денис
Дата: 2014-01-28

Комментарий добавил(а): Александр
Дата: 2014-02-24

Для школьников будет не понятно,а так все нормально

Комментарий добавил(а): Алла
Дата: 2014-04-30

Ольга, Вы умница! Нигде и никогда не пропускаю ни одного Вашего слова.

Комментарий добавил(а): надежда
Дата: 2014-10-22

Комментарий добавил(а): Валентина
Дата: 2014-09-18

Источник

2. Даны четыре точки А, В, С и D, причем А ¢ ВС. Докажите, что если. Зив Б.Г. Геометрия 10 класс. Самостоятельная работа 22. Вариант 7

ответ

2.
Дано а ║α, а ║β, b ║ α, b║ β. Каково должно быть взаимное расположение данных прямых, чтобы плоскости а и β были параллельными? ( Подробнее. )

Say you are fond of both things.

Example: I am fond of both fruit and vegetables. ( Подробнее. )

Решите задачу:
За 3 ч мотоциклист проезжает то же расстояние, что велосипедист за 5 ч. Скорость мотоциклиста на 12 км/ч больше ( Подробнее. )

Можете подсказать какие здесь будут правильные слова?
Choose the correct word. Check in the Word List. Then make a sentence with ( Подробнее. )

2.
Все грани параллелепипеда ABCDA1B1C1D1 — прямоугольники, М — внутренняя точка сечения АА1С1С. Постройте сечение параллелепипеда ( Подробнее. )

Источник

Введение (стр. 5 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5

8. Доказать, что центр симметрии параллелограмма ABCD совпадает с центром симметрии параллелограмма A¢B¢C¢D¢, если на евклидовой плоскости вершины параллелограмма ABCD лежат на сторонах параллелогремма A¢B¢C¢D¢, так что A Î (A¢B¢), B Î (B¢C¢), C Î (C¢D¢), D Î (D¢A¢).

§6. Сложное отношение четырех точек прямой

На проективной плоскости P2 возьмем прямую d. На прямой d возьмем проективный репер R=<A1, A2, E> и четыре различные точки А(а1,а2), В(b1,b2), С(с1,с2), D(d1,d2).

Определение. Сложным отношением четырех точек прямой называется число, которое выражается следующей формулой:

(1)

Кроче, , где (XY) – определитель из координат точек X и Y. Если на прямой d возьмем проективный репер R = <A, В, С>, то нетрудно доказать, что сложное отношение (АВ, CD) будет выражаться так:

, где D(d1,d2)<A, В, С>.

Свойства сложного отношения четырех точек прямой.

1. Сложное отношение четырех точек прямой не зависит от выбора проективного репера на прямой.

1. А, В, С различные точки прямой. Из формулы (1) следует, что D ¹ А.

Источник