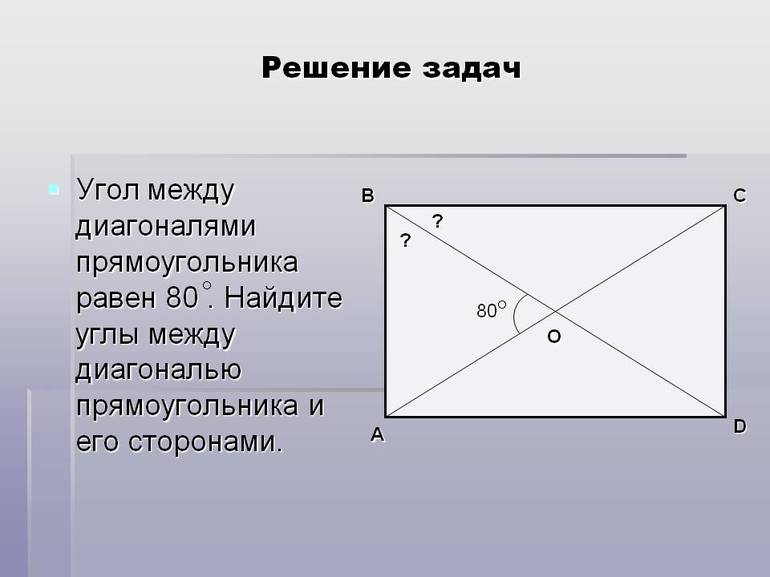
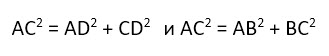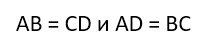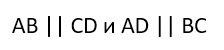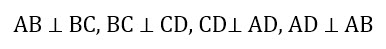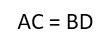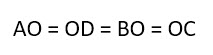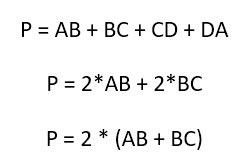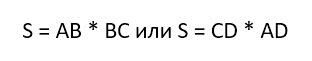Докажите что диагонали треугольника равны
Общая информация
В задачах по геометрии и физике приходится находить некоторые параметры прямоугольника: углы, стороны, периметр, площадь и диагонали. Все эти величины связаны между собой некоторыми соотношениями. Каждый должен уметь их рассчитывать, поскольку это необходимо не только для решения математических задач, но и в жизни. Например, при укладке керамзитной плитки на пол.
Используя свойство диагоналей, можно определить метод ее укладки. Кроме того, в физике иногда требуется рассчитать площадь поперечного сечения, а необходимая формула неизвестна. Во время планирования покупки строительных материалов нужно вычислить их количество, произведя вычисление площади или периметра помещения.
Однако формул для ведения расчетов недостаточно, поскольку нужно идентифицировать геометрическую фигуру. Для каждой из них применяются разные соотношения. В случае неверного определения вычисления окажутся недостоверными, а это негативно сказывается не только на экзаменах или контрольных, но и в финансовой сфере.
Сведения о прямоугольнике
Прямоугольником называется фигура с прямыми внутренними углами между смежными сторонами, у которой противоположные стороны равны. Его частным случаем, как говорят математики, является квадрат. У него все стороны равны, а углы также являются прямыми. Не каждый может правильно определить тип фигуры, поскольку от этого шага зависит правильность вычислений какого-либо параметра.
Для каждого геометрического тела существуют определенные критерии, по которым можно узнать его принадлежность. Эти критерии называются признаками. Некоторые новички путают признаки и свойства, но существует главное отличие, которое заключено в определении терминов «признак» и «свойство». Кроме того, специалисты предлагают простой способ, позволяющий избежать путаницы между терминами.
Идентификация или признаки
Признак — некоторые критерии, по которым можно отнести фигуру к определенному типу. Свойствами называются некоторые аксиомы и утверждения, полученные при доказательстве теорем. Идентифицировать прямоугольник можно с помощью теоремы из эвклидовой геометрии. Она имеет такую формулировку: если три угла фигуры являются прямыми, то она является прямоугольником. Для доказательства нужно выполнить такие действия:
Существуют также и другие признаки, по которым можно идентифицировать фигуру. По одному из них можно определить ее принадлежность к прямоугольнику. К признакам можно отнести такие:
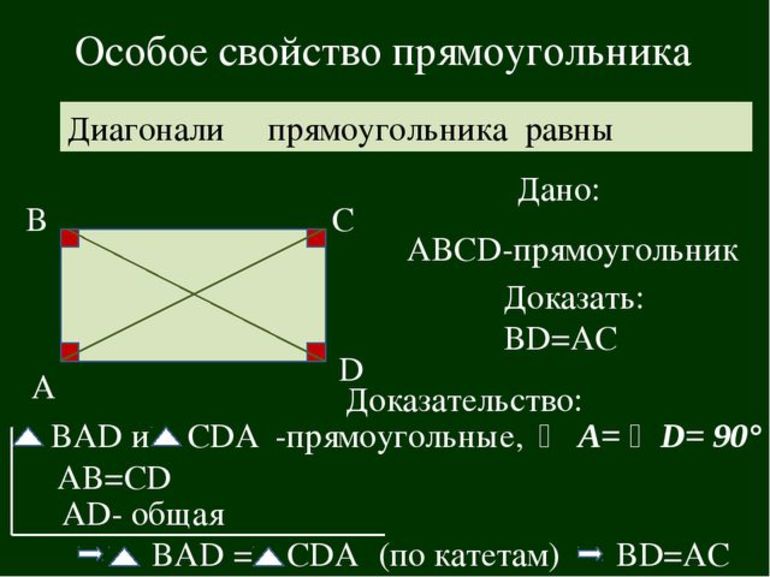
Первый и второй признаки получаются из основного определения фигуры. Третий признак является следствием доказательства теоремы, формулировка которой является следующей: диагонали прямоугольника равны. Она еще называется теоремой о диагоналях прямоугольника.
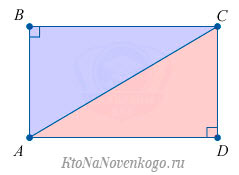
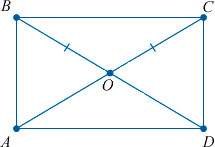
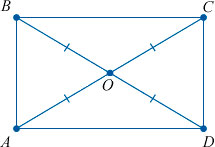
Для ее доказательства нужно начертить произвольный прямоугольник ABCD и провести в нем диагонали AC и BD. Они будут пересекаться в некоторой точке X. Они образуют прямоугольные треугольники ABC и ABD. В этом случае нужно доказать равенство треугольников. Они равны между собой: сторона АВ — общая, угол А равен В и сторона BC = AD (по равенству противоположных сторон). Из этого следует, что треугольники равны. Следовательно, их гипотенузы, которые также являются и диагоналями, равны.
Свойства фигуры
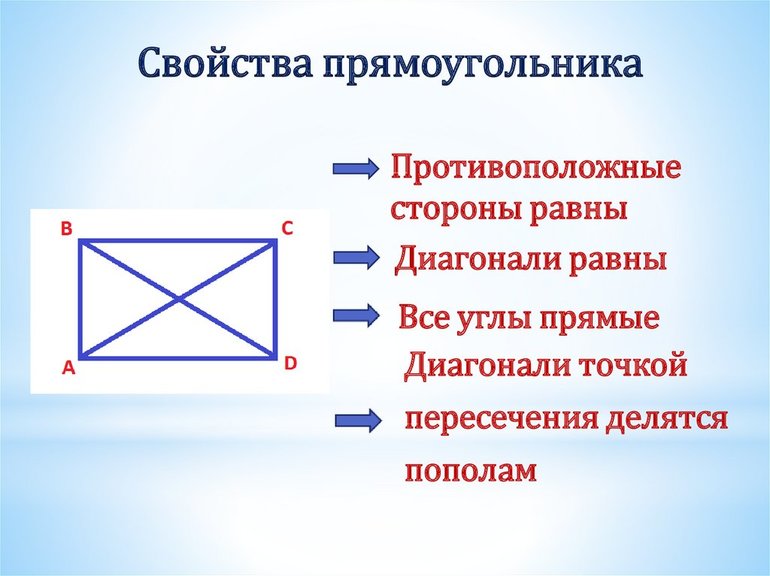
Необходимо отметить, что квадрат — правильный четырехугольник, поскольку у него все стороны равны. Результирующая формула диагонали прямоугольника будет выглядеть таким образом: d = (AB 2 + BC 2 )^(½). При решении задач применяются свойства прямоугольника:
Однако при решении задач свойств недостаточно. Для этого применяются специальные соотношения и формулы. Некоторые из них были получены из свойств фигуры. Во всех формулах будет браться радиус описанной окружности — R и ее диаметр — D, а также функция «sqrt», которая эквивалентна квадратному корню (x^(1/2) = x^(0.5)).
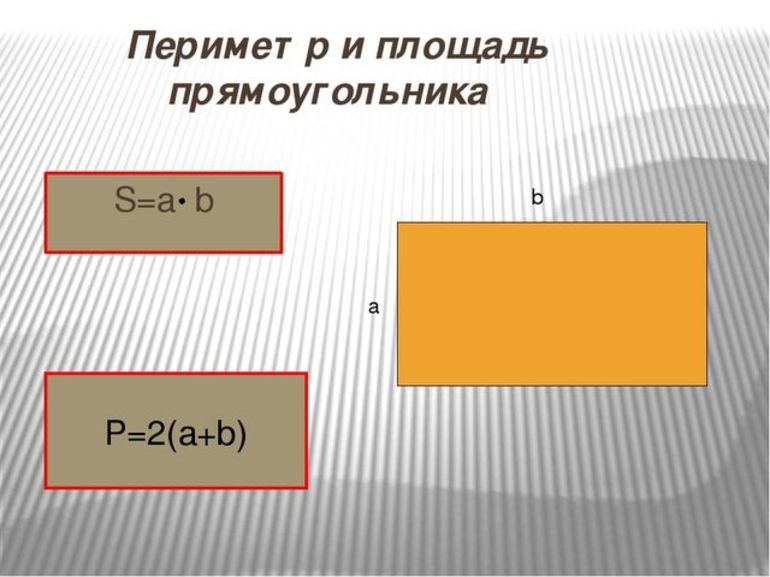
Периметр и площадь
Для удобства необходимо ввести некоторые обозначения. Диагонали следует обозначить литерой d, а противолежащие стороны — a и b, соответственно. Периметр — характеристика, соответствующая суммарному значению сторон фигуры. Очень часто ее обозначают литерой P. Существует также базовая формула: Р = 2а + 2b. Соотношение можно править таким способом: Р = 2 (a + b). Кроме того, существуют другие соотношения для определения P, когда известны некоторые параметры:
P и a (b): S = [(P * a) — 2a 2 ] / 2 = [(P * b) — 2b 2 ] / 2.
a (b) и d: S = a * sqrt[d 2 — a 2 ] = b * sqrt[d 2 — b 2 ].
Синус острого угла (Y) между двумя d и d: S = d 2 * sin (Y) / 2.
R и a (b): S = a * sqrt[4 * R 2 — a 2 ] = b * sqrt[4 * R 2 — b 2 ].
D и a (b): S = a * sqrt[D 2 — a 2 ] = b * sqrt[D 2 — b 2 ].
Для решения различных задач также могут быть полезны и другие соотношения, позволяющие найти не только диагонали, но и стороны прямоугольника.
Диагонали и стороны
Для оптимизации решения нужно знать формулы, с помощью которых можно находить одну из сторон или диагональ прямоугольника. Необходимо разобрать основные соотношения, по которым находятся стороны фигуры, когда известны следующие параметры:
Для нахождения диагонали также есть некоторые формулы. Для их применения следует знать такие параметры фигуры:
a и b: d = [a 2 + b 2 ]^(1/2).
S и a (b): d = (S 2 + a 4 )^(1/2) / a= (S 2 + b 4 )^(1/2) / b.
P и a (b): d = (P 2 — 4Pa + 8a 2 )^(1/2) / 2 = (P 2 — 4Pb + 8b 2 )^(1/2) / 2.
Однако это не все соотношения. В некоторых случаях разрешается описывать окружность вокруг фигуры. С помощью такого «геометрического хода» можно существенно упростить решение задачи. Это позволяет воспользоваться другими формулами.
Другие соотношения
Для решения задач используются и другие соотношения, которые позволяют найти параметры окружности, которая описана. Пусть дана окружность с радиусом R и диаметром D. Кроме того, известны некоторые параметры фигуры (a, b, d, P и S). С помощью формул можно найти D и R окружности при известных некоторых величинах:
a и b: R = (a 2 + b 2 )^(1/2) / 2.
P и a (b): R = (P 2 — 4Pa + 8a 2 )^(1/2) / 4 = (P 2 — 4Pb + 8b 2 )^(1/2) / 4.
S и a (b): R = (S 2 + a 4 )^(1/2) / 2a = (S 2 + b 4 )^(1/2) / 2b.
Пример решения
Пусть дана некоторая фигура, диагонали которой равны, а ее периметр равен 50. Одна из сторон a = 10. Следует провести идентификацию, а также найти такие параметры:
Данная задача является типом сложного класса, поскольку название фигуры не упоминается. Ее следует идентифицировать, а затем применить некоторые формулы для решения. Кроме того, необходимо верно выполнить 5 пункт. Однако не следует углубляться в строительную сферу. Бывают два метода укладки плитки: обычный — форма помещения является прямоугольником или квадратом, и с центра — другая фигура.
У фигуры диагонали равны, значит по третьему признаку она является прямоугольником. К нему можно применять вышеописанные формулы. Для нахождения другой стороны следует составить уравнение 2x + 2 * 10 = 50. Затем нужно перенести все известные значения в правую часть: 2х = 50 — 20. Далее можно найти переменную: х = 30 / 2 = 15 (ед.). Следует обратить внимание на написание единицы измерения. Если в условии задачи она не указана, то пишется единица измерения, которая заключается в круглые скобки. Достаточно найти только одну сторону, поскольку у прямоугольника существует свойство равенства противоположных сторон.
Значение диагоналей находится по формуле: d = [a 2 + b 2 ]^(1/2) = (15 2 + 10 2 )^(1/2) = (225 +100)^(1/2) = (325)^(1/2). Площадь можно найти таким образом: S = a * b = 15 * 10 = 150 [(ед.)^2]. Радиус вычисляется так:
R = (P 2 — 4Pa + 8a 2 )^(1/2) / 4 = (50 2 — 4 * 50 * 10 + 8 * 10 2 )^(1/2) / 4 = (1300)^(1/2) / 4 (ед.).
R = (S 2 + a 4 )^(1/2) / 2a = (150 2 + 100 4 )^(1/2) / (2 * 10) = (1300)^(1/2) / 4 (ед.).
Плитку можно укладывать обыкновенным способом, начиная не с центра, поскольку поверхность является прямоугольником. Все углы между сторонами равны между собой. Их градусная мера по 12 свойству соответствует 90.
Таким образом, при решении задач рекомендуется идентифицировать геометрическую фигуру, а затем применять к ней формулы.
Прямоугольник — это одна из основ геометрии
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.
Название это весьма говорящее, и в нем скрыто официальное определение.
Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.
Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.
Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».
Прямоугольник — это.
Все тот же Евклид разделил все четырехугольники на два вида – параллелограммы (что это?) и трапеции (что это?).
У первых противоположные стороны равны и параллельны, а у вторых параллельна только одна пара сторон, и они при этом не равны.
То есть выглядит это так:
Так вот, прямоугольник в данном случае является частным случаем параллелограмма.
У этой фигуры противоположные стороны параллельны. Это первое условие по Евклиду. И к тому же они равны, что является условием номер два.
У прямоугольника есть и собственный частный случай. Когда равны не только противоположные стороны, а все. И как нетрудно догадаться, фигура эта называется квадрат.
Ну, и логично предположить, что квадрат (как и сам прямоугольник) является частным случаем параллелограмма.
Признаки прямоугольника
Признаки геометрической фигуры – это совокупность отличий, по которым ее можно выделить среди других.
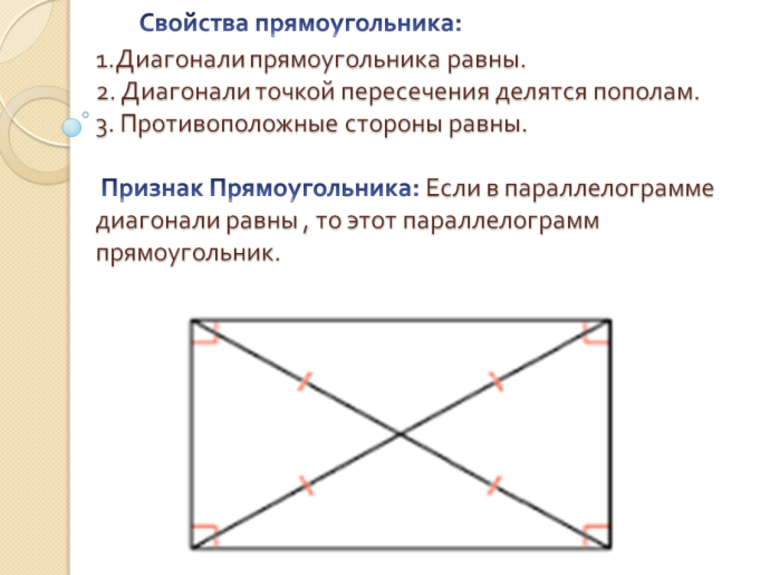
В случае с прямоугольником их всего три:
Диагонали прямоугольника
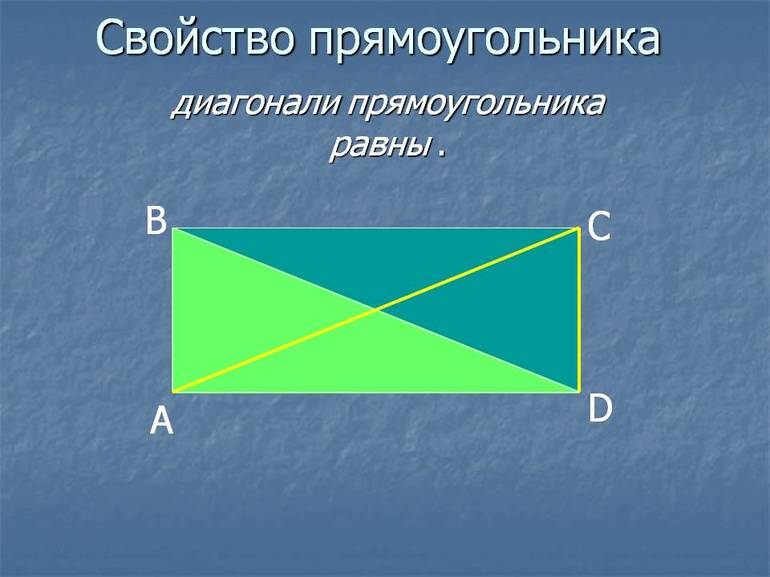
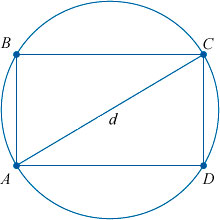
Как мы уже упомянули выше, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны между собой.
Доказать это можно с помощью известной теоремы Пифагора. Она гласит, что «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы».
В нашем случае гипотенузой является диагональ прямоугольника, которая делит его на два равных прямоугольных треугольника. И теорема Пифагора выглядит следующим образом:
Свойства прямоугольника
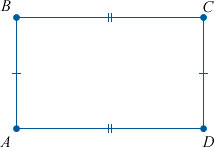
К свойствам прямоугольника относятся следующие утверждения:
Периметр и площадь
Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.
Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:
Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:
К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.
Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (5)
Главная основа геометрии — это все же треугольник. Через него можно построить любую фигуру и доказать любую теорему.
Не согласен с утверждением, что раз один угол прямой, то перед нами точно прямоугольник, всё же прямоугольник — это когда все противоположные стороны параллельны друг другу, а если только один угол прямой, то там и трапеция может быть.
Я бы сказала, что прямоугольник — это основа архитектуры. Все здания так или иначе используют эту фигуру в своем дизайне.
Вот за что я люблю прямоугольники, так за то, что площадь его легко найти, да и периметр, вот с трапецией сложнее, увы, но те же земельные участки больше трапеции, отсюда и земельные споры.
Четырехугольники
теория по математике 📈 планиметрия
Четырехугольник – это геометрическая фигура, состоящая из четырех точек, никакие три из которых не лежат на одной прямой, и отрезков, последовательно соединяющих эти точки.
Выпуклый четырехугольник
Четырехугольник называется выпуклым, если он находится в одной полуплоскости (то есть все его стороны расположены только с одной стороны прямой, прямая НЕ разбивает фигуру) относительно прямой, содержащей любую его сторону. На рисунке показан выпуклый четырехугольник АВСD.

Диагональ четырехугольника – отрезок, соединяющий любые две не соседние вершины. На рисунке 2 диагоналями являются отрезки АС и BD.
Виды и свойства выпуклых четырехугольников
Сумма углов выпуклого четырехугольника равна 360 градусов.
Прямоугольник
Прямоугольник – это четырехугольник, у которого все углы прямые.
S=ab, где a и b соседние стороны прямоугольника.
Квадрат
Квадрат – это прямоугольник, у которого все стороны равны.
Параллелограмм
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Ромб – это параллелограмм, у которого все стороны равны.
Трапеция
Трапеция – это четырехугольник, у которого только две противоположные стороны параллельны. Параллельные стороны называются основаниями трапеции, а две другие стороны – боковыми сторонами трапеции.
Виды трапеций
Трапеция называется прямоугольной, если у нее боковая сторона перпендикулярна основаниям. Прямоугольная трапеция имеет два прямых угла.
углы А и С равны по 90 градусов
Средняя линия трапеции
Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.
Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.
Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.
По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.е. АВ=СD, значит, АВ=BN=NC=CD. Таким образом, мы доказали, что BN=NC, т.е. N – середина ВС.
pазбирался: Даниил Романович | обсудить разбор | оценить
Сделаем чертеж, выполнив на нём дополнительные построения – высоты АМ и СН, которые равны как расстояния между параллельными сторонами трапеции.
pазбирался: Даниил Романович | обсудить разбор | оценить
Основания трапеции равны 7 и 11, а высота равна 7. Найти площадь этой трапеции.
Для нахождения площади трапеции в справочном материале есть формула
pазбирался: Даниил Романович | обсудить разбор | оценить
Для начала надо сделать построения на чертеже, чтобы увидеть, как располагаются известные и неизвестные элементы и чем они еще могут являться на чертеже.
с=44 √ 2 × √ 2 =44 √ 4 =44 × 2=88
pазбирался: Даниил Романович | обсудить разбор | оценить
Для выполнения данного задания надо подставить все известные данные в формулу:
Найдем неизвестный множитель, разделив 12,8 на 3,2: d 1 =12,8:3,2=4
pазбирался: Даниил Романович | обсудить разбор | оценить
На плане изображен дачный участок по адресу: п. Сосновка, ул. Зеленая, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.
При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв.м, а чуть подальше – жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6). Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой. К участку подведено электричество. Имеется магистральное газоснабжение.
Задание №1
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность четырех цифр без пробелов, запятых и других символов.
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры |
Решение
Для решения 1 задачи работаем с текстом и планом одновременно:
при входе на участок слева от ворот находится гараж (слева от входа находится объект под номером 2), итак, гараж — 2. Справа от ворот находится сарай площадью 24 кв.м (справа объект под номером 1), сарай – номер 1. А чуть подальше – жилой дом, следовательно, жилой дом – объект под номером 7. Напротив жилого дома расположены яблоневые посадки, на плане они обозначены цифрой 3. Также на участке есть баня, к которой ведет дорожка, выложенная плиткой, на плане видим, что к объекту под номером 4 ведет дорожка, значит баня – 4. Огород с теплицей внутри (огород отмечен на плане цифрой 6), в огороде расположена теплица – объект 5.
Итак, получили следующее:
1 – сарай; 2 – гараж; 3 – яблоневые посадки; 4 – баня; 5 – теплица; 6 – огород; 7 – жилой дом.
Заполняем нашу таблицу:
| Объекты | яблони | теплица | сарай | жилой дом |
| Цифры | 3 | 5 | 1 | 7 |
Записываем ответ: 3517
Задание №2
Плитки для садовых дорожек продаются в упаковках по 6 штук. Сколько упаковок плиток понадобилось, чтобы выложить все дорожки и площадку между сараем и гаражом?
Решение
Для начала надо определить, как обозначены дорожки, которые надо выложить плиткой, на плане. На плане они показаны серым цветом (мы их обведём голубым цветом).
Теперь ищем в условии задачи, что сказано про плитки и дорожки: «Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1м х 1м».
Сосчитаем, сколько клеточек (плиток) на плане, получаем 65. Зная по условию задачи 1, что плитки продаются в упаковках по 6 штук, разделим 65 на 6. Заметим, что 65 на 6 не делится, получается приблизительно 10,8…Учитывая, что упаковки не делятся, округляем до большего целого числа, нам понадобится 11 упаковок.
Задание №3
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками по прямой) в метрах.
Решение
Из задания 1 знаем, что жилой дом обозначен на плане цифрой 7, а теплица цифрой 5. Следовательно, на плане находим эти объекты и расстояние между двумя ближайшими точками по прямой (обозначим это голубым цветом). Видим, что это расстояние – 2 клетки. На плане показано, что длина стороны одной клетки равна 2 метра, значит, расстояние между двумя этими объектами равно 4 метра.
Задание №4
Найдите площадь, которую занимает гараж. Ответ дайте в квадратных метрах.
Решение
Найдем на плане гараж, это объект под номером 2. Гараж имеет прямоугольную форму, следовательно, нам надо найти площадь прямоугольника. Для этого надо найти длину и ширину. На плане показано, что длина стороны 1 клетки равна 2 метра, значит, длина гаража равна 8 м (4 клетки), а ширина — 6 м (3 клетки).
Зная ширину и длину, находим площадь гаража: 6х8=48 кв.м
Задание №5
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв.м., а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски и стоимость доставки заказа даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,25 кг/кв.м | 6 кг | 3000 руб. | 500 руб. |
| 2 | 0,4 кг/кв.м | 5 кг | 1900 руб. | 800 руб. |
Во сколько рублей обойдется наиболее дешёвый вариант покупки с доставкой?
Решение
Определим, сколько килограммов краски понадобится для покраски забора площадью 232 кв.м:
1 магазин: 232х0,25=58 кг
2 магазин: 232х0,4=92,8 кг
Вычислим количество банок краски, которое надо купить, зная массу краски в 1 банке:
1 магазин: 58:6=9,7…; так как банки продаются целиком, то надо 10 банок (округляем до наибольшего целого числа)
2 магазин: 92,8:5=18,56; значит надо 19 банок.
Вычислим стоимость краски в каждом магазине плюс доставка:
1 магазин: 10х3000+500=30500 руб.
2 магазин: 19х1900+800=36900 руб.
Из решения задачи видно, что в 1 магазине купить краску выгоднее. Следовательно, наиболее дешёвый вариант покупки с доставкой будет стоить 30500 рублей.
pазбирался: Даниил Романович | обсудить разбор | оценить