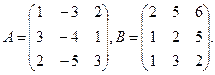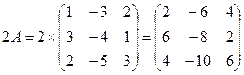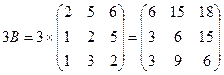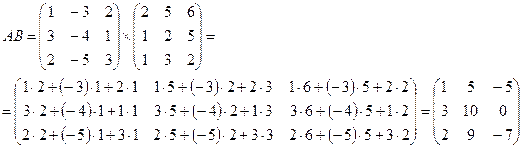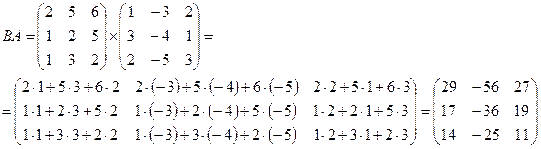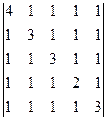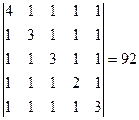Докажите что диагональные матрицы перестановочные
Доказать утверждение о вещественной треугольной матрице

Как привести матрицу к унитреульной матрице или верхней треугольной матрице? Добавлено через 14.
Доказать утверждение
Объясните, как доказать или опровергнуть утверждение о произвольных множествах A, B, C методом.
Доказать утверждение
Подскажите, как быть с такими гипотезами, что то торможу, как аксиомы применить к такому, похоже.
Доказать утверждение
Доказать,что пересечение двух подгрупп А и В группы G будет подгруппой конечного индекса в группе.
Нет: a11^2 + a12^2 + a13^2; a22^2 + a23^2; a33^2.
Решение
Значит, матрицы A еще нет (то есть она не дана), и ее существование нужно доказать.
Диагонализируемость в данном случае не нужна, да ее и нет, как правило.
Треугольная матрица Х вычисляется из уравнения X 2 =C для треугольной же матрицы С с положительной диагональю так. Вначале вычисляем диагональные элементы из уравнений
» />
Затем, зная диагональные элементы Х и учитывая положительность диагональных элементов С, вычисляем элементы, стоящие на диагонали, параллельной главной, из формулы
» />
После этого переходим к следующей диагонали и т.д.
Рекомендую проделать все выкладки для матриц порядков 2, 3, 4. Все станет ясно.
Доказать утверждение
Докажите, что любое счетное линейно упорядоченное множество изоморфно некоторому подмножеству.
Доказать утверждение
Помогите доказать, пожалуйста:help:
Доказать утверждение
Здравствуйте. Как доказать следующее утверждение: Изоморфные графы имеют одинаковые хроматические.
Доказать утверждение
Подскажите пожалуйста как доказываются такого рода утверждения: A\subseteq B тогда и только тогда.
Являются ли матрицы перестановочными
Вариант №3
Задание № 1. Алгебра матриц
2) Произведение матриц АВ и ВА. Выяснить, является ли данные матрицы перестановочными.
Решение.
1) Найдем 2А:
Найдем 3B:
Вычисляем 2А-3В: 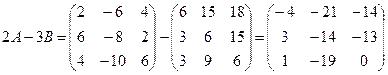
2)
Так как АВ≠BA, то матрицы А и В не являются перестановочными.
Задание № 2. Определители
Вычислить определитель пятого порядка:
Решение.
Запишем матрицу в виде:
Преобразуем 1-ый столбец таким образом, чтобы в нем оказалось максимальное количество нулей.
Полученную матрицу разложим по элементам 1-ого столбца и преобразуем ее:
Добавим 4-ую строку к 3-ой:
| C 3 +C 4 = | 11 /4 | 3 /4 | 3 /4 | 3 /4 |
| -2 | ||||
| -2 | ||||
| -1 |
Добавим 3-ую строку к 4-ой:
| C 4 +C 3 = | 11 /4 | 3 /4 | 3 /4 | 3 /4 |
| -2 | ||||
| -2 | ||||
| -2 | -1 |
Умножим 1-ую строку на (k = 2 / 11 /4 = 8 /11) и добавим к 2-ой:
| C 2 + 8 /11C 1 = | 11 /4 | 3 /4 | 3 /4 | 3 /4 |
| 28 /11 | 6 /11 | 6 /11 | ||
| -2 | ||||
| -2 | -1 |
Полученную матрицу разложим по элементам первого столбца и преобразуем ее:
Умножим 1-ую строку на (k = 2 / 28 /11 = 11 /14) и добавим к 2-ой:
| C 2 + 11 /14C 1 = | 28 /11 | 6 /11 | 6 /11 |
| 3 /7 | 17 /7 | ||
| -1 |
Полученную матрицу разложим по элементам первого столбца и преобразуем ее:
Определитель равен ∆ = 4 * 11 /4 * 28 /11 * ( 3 /7*2 – (-1)* 17 /7) = 92
Ответ:
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9530 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Доказать, что для того чтобы квадратная матрица А была перестановочна со всеми квадратными матрицами того же порядка, необходимо и достаточно, чтобы матрица А была скалярной.
Пусть порядок А равен n и для любой квадратной матрицы B порядка n выполнено AB = BA.
Рассмотрим в качестве матрицы B матрицу, у которой все элементы равны нулю, кроме i-го диагонального. Пусть он равен d.
Тогда в AB все стобцы будут нулевые, кроме i-го, который будет равен i-му столбцу матрицы A, умноженному на d.
Перебирая все i от 1 до n, получаем, что матрица A необходимо должна быть диагональной. Теперь докажем что она должна быть скалярной.
Рассмотрим в качестве матрицы B матрицу элементарного преобразования, которое меняет местами 1-ый и i-ый столбцы.
Рассматриваются матрицы, результатом умножения которых на любую прямоугольную матрицу является перестановка ее строк или столбцов.
Непосредственным вычислением легко проверяются следующие свойства матрицы перестановок.
Таким образом, если в i-ой строке матрицы перестановок P единица расположена в j-ом столбце, то умножение матрицы P слева на матрицу A приводит к перемещению j-ой строки матрицы A в позицию i-ой строки.
Аналогично, если в i-ом столбце матрицы перестановок P единица расположена в j-ой строке, то умножение матрицы P справа на матрицу A приводит к перемещению j-го столбца матрицы A в позицию i-го столбца.
Если матрицы перестановок P получена из единичной матрицы E перестановкой местами двуз строк (или двух столбцов), то такая матрица называется элементарной матрицей перестановок.
При умножение слева элементарной матрицы перестановок на матрицу A происходит перестановка соответствующих строк матрицы A.
Умножение справа элементарной матрицы перестановок на матрицу A приводит к перестановке соответствующих столбцов матрицы A.
Для любой матрицы перестановок P справедливы следующие свойства:
где 
где 
Терема 1. Произведение матриц перестановок одного и того же порядка есть матрица перестановок.
Терема 2. Матрица перестановок n-го порядка может быть представлена в виде произведения (n – 1) элементарных матриц перестановок.
Терема 3. Квадрат элементарной матрицы перестановок есть единичная матрица.
Описание файла
Просмотр DJVU-файла онлайн
Найти е’,Ае, если А = (а; ) е К «», а е’, и е — единичные строка и столбец подходящих размеров. 1.14. Мапгричной единицей Е, размера т х и называется матрица, у которой элемент в позиции (г, г) равен единице, а все остальные элементы равны нулю. Для произвольной матрицы А и матричной единицы Е,б подходящего размера вычислить: а) АЕеб б) Е, А. 1.15. Найти ДА): а) Д
х) = хг — 2х+ 2, А = б)
6 2) произведение А
6 Глава 1. Матрицы 1.16. Доказать, что каждая квадратная матрица второго по-
с х — (а+ а1)х+ (ай — бс) = О. 1.17. Доказать, что если А — диагональная матрица, то матрица ДА) также диагональная, каков бы ни был многочлен Дх). 1.18. Вычислить: а) ; б) — 2 — 4 0 1.19.
Вычислить а),; б) д) 1 О,п>2; е) ) О Л ‘ ) О 1 спаса — в1па 1 в1па спаса
= (А+ В)(А — В). 1.24. Доказать, что если матрицы А и В перестановочны, то: а) 4з+ Вз (4+ ВИАз 4В+ Вз). б) (А+ В) А +С,’,А22-
В + + В 1.25. Найти п-ю степень матрицы А, если матрица А равна: 6)
— 4 — 5 10 11 Аа Азв 1.26. В ычислить матрицу + + + +, если матрица А равна:
— 2 — 21′ )[ а) 2 2,’ б) 1.27. Найти все если: )А=
— 2 — 21 матрицы, перестановочные с матрицей А, б)А= 2 1, в)А= 0100 0010 0001 г) А= 0000 ) А — квадратна е я матрица и-го порядка, все элементы которой равны единице. 1.28. Доказать, что умножение матрицы А слева на диагональную матрицу 1А’ = 222а81Лц Лз. Л„) равносильно умноже- )А= [ б) А= 1010’с2 — 1о — 1’23 с2 — 1 22 ‘ — 10 — 9 д) А — матричная единица В2.
Е 222″ 22; Глава 1. Матрицы нию строк А соответственно на Лы Лз. Л„, умножение же А на Р справа равносильно аналогичному изменению столбцов. 1.29. Найти матрицу А, если И,’И 2 5 А= 1.30. Доказать, что если А — диагональная матрица и все элементы ее главной диагонали различны между собой, то любая матрица, перестановочная с А, также диагональна. 1.31. Доказать, что квадратная матрица А перестановочна со всеми диагональными матрицами тогда и только тогда, когда она сама является диагональной. 1.32.
Доказать, что квадратная матрица А перестановочна со всеми квадратными матрицами того же порядка тогда и только тогда, когда она является скалярной. 1.33. Доказать, что если матрица А перестановочна с матрицей В, то она перестановочна и с матрицей В
. Верно ли обратное? 1.34. Пусть А — квадратная матрица и 1(х) и д(х) — произвольные многочлены. Показать, что матрицы 1(А) и д(А) перестановочны.
1.35. Доказать, что след матрицы обладает следующими свойствами: а) сг(А+ В) = сгА+ сгВ; б) сг(аА) = асгА; в) сг(Ат) = сгА; г) сг(АВ) = сг(ВА), если произведения АВ, ВА определены. 1.36. Доказать, что для любой матрицы величина Сг(АтА) неотрицательна, причем равна нулю тогда и только тогда, когда матрица А нулевая. 1.36.1. Существуют ли матрицы А и В, для которых равенство АХВ = Х
выполняется при любой матрице Х б К
«»? 1.36.2. Можно ли свести операцию транспонирования матрицы общего вида к операциям умножения ее слева и справа на какие-либо наперед заданные матрицы? 1.37.
Доказать, что для любых квадратных матриц А и В одинакового размера их коммутатор [А, В] имеет нулевой след. 1.38. Доказать, что равенство [А, В] = 1 не выполнено ни для каких вещественных матриц А и В. 19 з1. Операции над матрицами и [аб) Е К'»»» величина т, =
си 1=1 т суммой, а величина с =
=1 1.39. Для матрицы А = называется ее г-й стпрочной
-й столбцовой суммой. а) Показать, что т
Считая, что произведение АВ определено, доказать, что все строчные суммы в АВ также одинаковы и равны ар’. в) Сформулировать и доказать столбцовый вариант утверждения пункта «б». 1.40. Доказать, что если квадратные матрицы А и В порядка и таковы, что для любого вектор-столбца С Е К»»
выполнено соотношение Ас = Вс, то А = В. 1.41.
Доказать, что если квадратные матрицы А и В порядка и таковы, что для любых вектор-столбцов С, и Е К»»» выполнено соотношение с,
Ви, то А = В. 1.42. Найти коммутатор матричных единиц Е, и Еы и показать, что он нулевой тогда и только тогда, когда либо г = у = 1с = 1, либо [1 — 1с) [1 — 1) ф О. 1.43. Доказать, что диагональная матрица с нулевым следом является линейной комбинацией коммутаторов матричных единиц. 1.44. Показать, что коммутатор обладает следующими свойствами: Глава 1, Матрицы 20 1.45. Доказать,что равенство [[А, В],С] = [А, [В,С)] выполнено тогда и только тогда, когда матрицы [А, С] и В пере- становочны.
1.46. Доказать, что для любых матриц А, В, С второго по- рядка выполнено соотношение [[[А, В]) г, С] = О. 1.47. Доказать, что любая матрица с нулевым следом явля- ется суммой коммутаторов матриц с нулевым следом. 1.48. Доказать, что для любой матрицы А с нулевой глав- ной диагональю найдутся матрица Х и диагональная матрица Р такая, что [Х, Р) = А. 1.49. Произведениелл Йордана А в В квадратных матриц А и В одного порядка называется матрица 1[АВ + ВА). Показать, что произведение Иордана обладает следующими свойствами: а) А*В = В в А; б) [сгА) в В = сгА * В; в) [А+В) е С= А*С+В*С; г) А*А = Аг; д) А*1=А; В)т Ат „Вт, ж) [Аг в В) * А = Аг * [В* А), выполненными для любых квадратных матриц А, В, С и еди- ничной матрицы 1 одного порядка.
2.2. Найти количество операций умножения, необходимых для вычисления произведения двух треугольных матриц порядка и одного вида. 2.3. Пусть А = (а,у) — треугольная матрица и-го порядка и »с Е (Ч. Найти йг А». 2.4. Доказать, что для любой треугольной матрицы А с положительными диагональными элементами найдется треугольная матрица В того же вида с положительными диагональными элементами такая, что В
, то произведению АВ соответствует блочная матрица С = (Сс ) с элементами з Ссс =
АссВсг. с=с 2.8. Применяя описанное в предыдущей задаче правило умножения блочных матриц, вычислить й— ‘[4— б) [ — 1 — 1 — 2 — 1 0 0 100 011 001 — 2 в)012 110 1;г)202 — 110 ной.
2.6. Квадратная матрица А порядка п.называется ленпсочной, если для некоторого числа т (меньшего и — 1) все элементы а; с индексами, удовлетворяющими условию
с — Я ) т, равны нулю. Число 2т+ 1 называется шириной ленты. Найти ширину ленты произведения ленточных матриц, если для сомножителей эта ширина равна 2псс + 1, 2тг + 1 соответственно и тс + тг