Докажите что две плоскости перпендикулярные одной прямой параллельны
§ 11. Параллельность плоскостей
11.1 Параллельность плоскостей, перпендикулярных одной прямой
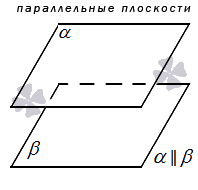
Напомним, что две плоскости, не имеющие общих точек, называются параллельными. Из теоремы о плоскости, перпендикулярной прямой (п. 9.2), следует, что две плоскости, перпендикулярные одной прямой, параллельны (рис. 99). Действительно, такие плоскости не имеют общей точки. В противном случае через одну точку проходили бы две плоскости, перпендикулярные одной прямой, что невозможно по указанной теореме.
Вспомните, что аналогичный признак параллельности прямых был доказан в планиметрии.
Доказанный нами простой признак параллельности плоскостей позволяет построить такие плоскости. Для этого достаточно взять какую-нибудь прямую и построить две перпендикулярные ей плоскости (п. 9.2).
11.2 Прямая, перпендикулярная двум параллельным плоскостям
Зависимость между параллельностью плоскостей и перпендикулярностью прямой и плоскости аналогична зависимости между параллельностью прямых и перпендикулярностью прямой и плоскости (теорема 9), рассмотренной в § 8. А именно наряду с доказанным в 11.1 признаком параллельности плоскостей имеет место и следующее обратное ему утверждение:
| Теорема 12 (о прямой, перпендикулярной параллельным плоско стям). Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой. |
Эта теорема является ещё одним признаком перпендикулярности прямой и плоскости. При её доказательстве используются две простые леммы:
| Лемма 1 (о пересечении параллельных плоскостей третьей плоскостью). Прямые, по которым две параллельные плоскости пересекают третью плоскость, параллельны. |
Доказательство. Пусть параллельные плоскости α и β пересекают плоскость γ по прямым а и b соответственно (рис. 100). Прямые а и b лежат в одной плоскости γ. Они не имеют общих точек, так как плоскости α и β не имеют общих точек. Поэтому прямые а и b параллельны.
| Лемма 2 (о прямой, пересекающей параллельные плоскости). Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую из них. |
Доказательство. Пусть плоскости α и β параллельны и прямая с пересекает плоскость α в точке А (рис. 101).
Возьмём в плоскости β любую точку М и проведём через прямую с и точку М плоскость γ. Она пересечёт плоскости α и β по параллельным прямым а и b.
Прямая с лежит в плоскости γ и пересекает прямую а в точке А. Поэтому прямая с пересечёт и прямую b, параллельную прямой а и лежащую в плоскости γ, в некоторой точке В. Точка В и является точкой пересечения прямой с и плоскости β, так как лежать в плоскости р прямая с не может (объясните!).
Теперь докажем теорему 12. Доказательство теоремы 12. Пусть плоскости α и β параллельны и прямая с перпендикулярна плоскости α (рис. 102).
Прямая с пересекает плоскость α в некоторой точке А. Поэтому по лемме 2 прямая с пересекает и плоскость β в некоторой точке В. Проведём через точку В в плоскости β любую прямую b и покажем, что с ⊥ b.
Пусть γ — плоскость, проходящая через прямые b и с. Она пересекает плоскости α и β по параллельным прямым а и b (по лемме 1). Так как с ⊥ α, то с ⊥ a. А поскольку b||а и все прямые а, Ь, с лежат в плоскости γ, то с ⊥ b. Следовательно, с ⊥ β (по определению перпендикулярности прямой и плоскости)
11.3 Основная теорема о параллельных плоскостях
| Теорема 13. Через каждую точку, не лежащую в данной плоскости, проходит плоскость, параллельная данной, и притом только одна. |
Доказательство. Пусть даны плоскость α и не лежащая в ней точка А (рис. 103). Проведём через точку А прямую а, перпендикулярную плоскости α (см. п. 9.1). Через точку А проведём плоскость β, перпендикулярную прямой а (см. п. 9.2). Плоскости α и β параллельны, так как они перпендикулярны прямой а. Мы доказали существование плоскости β, проходящей через точку А и параллельной плоскости α.
Докажем единственность такой плоскости. Пусть γ — плоскость, проходящая через точку А и параллельная плоскости α. Так как γ||α и а ⊥ α, то а ⊥ γ (по теореме 12). А поскольку через точку А проходит лишь одна плоскость, перпендикулярная прямой а (п. 9.2), то плоскости β и γ совпадают. Поэтому β — единственная плоскость, проходящая через точку А и параллельная плоскости α.
Следствие (о двух плоскостях, параллельных третьей). Две плоскости, параллельные третьей плоскости, параллельны.
Доказательство. Если две плоскости α и β параллельны плоскости γ, то они не имеют общей точки: в противном случае через эту точку проходят две плоскости, параллельные γ.
Замечание. Обратите внимание на аналогию с параллельными прямыми на плоскости: начиная с определения всем доказанным здесь предложениям о параллельных плоскостях соответствуют такие же предложения о параллельных прямых на плоскости. Сформулируйте их.
Лекция по геометрии на тему: «Перпендикулярность в пространстве». 10-й класс
Разделы: Математика
Класс: 10
Тема: Перпендикулярность прямой и плоскости.
Определение: Две прямые в пространстве могут пересекаться. (Привести примеры перпендикулярных прямых, используя окружающую обстановку).
Лемма: Если одна из двух прямых перпендикулярна к третьей прямой, то другая прямая перпендикулярна к этой прямой.
Дано: a || b, a 
Доказать: b 
Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
(Возможна запись: a 


Прямая, перпендикулярная к плоскости пересекает эту плоскость.
a 





Теорема: Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая также перпендикулярна к этой плоскости.
Дано: a || b, a 
Доказать: b 
Проведем в плоскости 



Теорема (обратная): Если 2 прямые перпендикулярны к плоскости, то они параллельны.
(Доказать предлагается учащимся самостоятельно).
Теорема: Если прямая, не лежащая в плоскости перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то прямая и плоскость перпендикулярны.
Предлагается 2 способа доказательства.
Дано: a 




Доказать: a 
Дано: m



Доказать: l 
Проведем прямую p так, чтобы O 











Замечание: Еще одно доказательство теоремы в учебнике “Геометрия 10-11” Л.С. Атанасяна и др.
Свойства перпендикулярных прямой и плоскости:
Теорема: Через любую точку пространства не принадлежащую плоскости проходит прямая перпендикулярная к данной плоскости, и притом только одна.
Дано: 

Доказать: 


. Что и требовалось доказать
. Существует ли прямая перпендикулярная к прямым а и b?
Параллельные плоскости, признак и условия параллельности плоскостей
В данной статье будут изучены вопросы параллельности плоскостей. Дадим определение плоскостям, которые параллельны между собой; обозначим признаки и достаточные условия параллельности; рассмотрим теорию на иллюстрациях и практических примерах.
Параллельные плоскости: основные сведения
Параллельные плоскости – плоскости, не имеющие общих точек.
На чертеже, как правило, плоскости, параллельные друг другу, отображаются как два равных параллелограмма, имеющих смещение относительно друг друга.
Параллельность плоскостей: признак и условия параллельности
В процессе решения геометрических задач зачастую возникает вопрос: а параллельны ли заданные плоскости между собой? Для получения ответа на этот вопрос используют признак параллельности, который также является достаточным условием параллельности плоскостей. Запишем его как теорему.
Плоскости являются параллельными, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
В практике для доказательства параллельности, в том числе, применяют две следующие теоремы.
Если одна из параллельных плоскостей параллельна третьей плоскости, то другая плоскость или также параллельна этой плоскости, или совпадает с ней.
Если две несовпадающие плоскости перпендикулярны некоторой прямой, то они параллельны.
На основе этих теорем и самого признака параллельности доказывается факт параллельности любых двух плоскостей.
Для параллельности заданных плоскостей α и β необходимо и достаточно, чтобы система линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имела решения (являлась несовместной).
Предположим, что заданные плоскости, определяемые уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 являются параллельными, а значит не имеют общих точек. Таким образом, не существует ни одной точки в прямоугольной системе координат трехмерного пространства, координаты которой отвечали бы условиям одновременно обоих уравнений плоскостей, т.е. система A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имеет решения. Если указанная система не имеет решений, тогда не существует ни одной точки в прямоугольной системе координат трехмерного пространства, чьи координаты одновременно отвечали бы условиям обоих уравнений системы. Следовательно, плоскости, заданные уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 не имеют ни одной общей точки, т.е. они параллельны.
Разберем использование необходимого и достаточного условия параллельности плоскостей.
Решение
Запишем систему уравнений из заданных условий:
Проверим, возможно ли решить полученную систему линейных уравнений.
Отметим, что, если бы мы применили для решения системы линейных уравнений метод Гаусса, это дало бы тот же результат.
Ответ: заданные плоскости параллельны.
Необходимое и достаточное условие параллельности плоскостей возможно описать по-другому.
Чтобы две несовпадающие плоскости α и β были параллельны друг другу необходимо и достаточно, чтобы нормальные векторы плоскостей α и β являлись коллинеарными.
Доказательство сформулированного условия базируется на определении нормального вектора плоскости.
n 1 → = t · n 2 ⇀ ⇔ A 1 = t · A 2 B 1 = t · B 2 C 1 = t · C 2
Решение
Для получения координат нормального вектора плоскости x 12 + y 3 2 + z 4 = 1 приведем это уравнение к общему уравнению плоскости:
Ответ: плоскости α и β не совпадают; их нормальные векторы коллинеарные. Таким образом, плоскости α и β параллельны.
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок № 8 Перпендикулярность прямой и плоскости
Перечень вопросов, рассматриваемых по теме
Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости
Теорема о прямой перпендикулярной к плоскости. Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл. Базовый и профильный уровень. М.: Просвещение, 2015. С.1-10.
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 9 класса. Базовый и профильный уровень
Зив Б.Г. Геометрия. Дидактические материалы. 10-11 класс М.: Просвещение, 2015.
Открытые электронные ресурсы:
Перпендикулярность прямой и плоскости. http://school-collection.edu.ru // Единая коллекция цифровых образовательных ресурсов.
Перпендикулярность прямой и плоскости. https://www.yaklass.ru // Я-класс. Образовательный портал Сколково.
Теоретический материал для самостоятельного изучения
Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой..
Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
Проведем какую-нибудь прямую x в плоскости α, т.е. x ∊ α.Так как а ⊥ α, то а ⊥ x.
По лемме о перпендикулярности двух параллельных прямых к третьей а1 ⊥ x.
Таким образом, прямая а1 перпендикулярна к любой прямой, лежащей в плоскости α, т. е. а1 ⊥ α
Теорема. Ели две прямые перпендикулярны плоскости, то они параллельны.
Через какую-нибудь точку М прямой b проведем прямую b1, параллельную прямой а.
Докажем, что прямая b1 совпадает с прямой b. Тем самым будем доказано, что а ‖ b. Допустим, что прямые b1 и b не совпадают. Тогда в плоскости β, содержащей прямые b и b1, через точку М проходят две прямые, перпендикулярные к прямой с, по которой пересекаются плоскости α и β. Но это невозможно, следовательно, а ‖ b, т.е. b ∊ β, b1 ∊ β, α 
Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.
Теорема. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Пусть дана плоскость α и точка М (см. рис. 2). Нужно доказать, что через точку М проходит единственная прямая с, перпендикулярная плоскости α.
Проведем прямую а в плоскости α (см. рис. 3). Согласно доказанному выше утверждению, через точку М можно провести плоскость γ перпендикулярную прямой а. Пусть прямая b – линия пересечения плоскостей α и γ.
В плоскости γ через точку М проведем прямую с, перпендикулярную прямой b.
Прямая с перпендикулярна b по построению, прямая с перпендикулярна а (так как прямая а перпендикулярна плоскости γ, а значит, и прямой с, лежащей в плоскости γ). Получаем, что прямая с перпендикулярна двум пересекающимся прямым из плоскости α. Значит, по признаку перпендикулярности прямой и плоскости, прямая с перпендикулярна плоскости α. Докажем, что такая прямая с единственная.
Предположим, что существует прямая с1, проходящая через точку М и перпендикулярная плоскости α. Получаем, что прямые с и с1 перпендикулярны плоскости α. Значит, прямые с и с1 параллельны. Но по построению прямые с и с1пересекаются в точке М. Получили противоречие. Значит, существует единственная прямая, проходящая через точку М и перпендикулярная плоскости α, что и требовалось доказать.
Теоретический материал для углубленного изучения
Теорема о прямой перпендикулярной к плоскости. Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.
Доказательство (см. рис. 1)
Пусть нам дана прямая а и точка М. Докажем, что существует плоскость γ, которая проходит через точку М и которая перпендикулярна прямой а.
Через прямую а проведем плоскости α и β так, что точка М принадлежит плоскости α. Плоскости α и β пересекаются по прямой а. В плоскости α через точку М проведем перпендикуляр MN (или р) к прямой а, 
Примеры и разборы решения заданий тренировочного модуля
Выбор элемента из выпадающего списка
Выпишите ребра, перпендикулярные плоскости (DC
Правильный вариант/варианты (или правильные комбинации вариантов):
Неправильный вариант/варианты (или комбинации):
Подсказка: в кубе все углы по 


Закончите предложение, чтобы получилось верное утверждение.
Правильный вариант/варианты (или правильные комбинации вариантов):
Две прямые называются перпендикулярными, если …
угол между ними равен 90
Если плоскость перпендикулярна одной из двух параллельных прямых, то она …
перпендикулярна и другой
Неправильный вариант/варианты (или комбинации):
Лемма: Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к третьей прямой.
Теорема: если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.