Докажите что две прямые перпендикулярные одной и той же плоскости параллельны
Две прямые, перпендикулярные одной и той же плоскости, параллельны
Пусть даны плоскость и не лежащая на ней точка:
— перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости;
— конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра;
— расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость;
— наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости;
— конец отрезка, лежащий в плоскости, называется основанием наклонной;
— отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
Теорема о трех перпендикулярах:
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
Две пересекающиеся плоскости, называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.
Через центр вписанной в треугольник окружности проведена прямая, перпендикулярная плоскости треугольника. Докажите, что каждая точка этой прямой равноудалена от сторон треугольника.
Пусть А, В, С – точки касания сторон треугольника с окружностью, О – центр окружности и S – точка на перпендикуляре. Так как радиус ОА перпендикулярен стороне треугольника, то по теореме о трех перпендикулярах отрезок SА есть перпендикуляр к этой стороне, а его длина – расстояние от точки S до стороны треугольника. По теореме Пифагора SА= 


1. Даны прямая а и плоскость 

2. Докажите, что если прямая параллельна плоскости, то все ее точки находятся на одинаковом расстоянии от плоскости.
3. Из точки к плоскости проведены две наклонные, одна из которых на 20 см больше другой. Проекции наклонных равны 10 см и 30 см. Найдите наклонные.
4. Сторона квадрата равна 4 см. Точка, равноудаленная от всех вершин квадрата, находиться на расстоянии 6 см от точки пересечения его диагоналей. Найдите расстояние от этой точки до вершин квадрата.
5. Из точки к плоскости проведены две наклонные, равные 10 см и 17 см. Разность проекций этих наклонных равна 9 см. Найдите проекции наклонных.
6. Из точки к плоскости проведены две наклонные, равные 23 см и 33 см. Найдите расстояние от этой точки до плоскости, если проекции наклонных относятся как 2:3.
8. Прямая а перпендикулярна плоскости АВС. MD = 13. АС = 15, ВС = 20. АС 

9. Катеты прямоугольного треугольника ABC (С =90°) равны 4 см и 3 см. Точка М находится на расстоянии √6 см от плоскости треугольника ABC и на одинаковом расстоянии от всех его вершин. Найти расстояние от точки М до вершин треугольника.
1. Математика: учебник для учреждений нач. и сред. проф. образования / М.И. Башмаков. –М.: Издательский центр «Академия», 2010 г.
Самостоятельная работа № 5.
Решение задач на подсчет числа размещений, перестановок.
Цель занятия: освоить методы решения задач на расчет количества выборок
Комбинаторика — часть математики, которая посвящена решению задач выбора и расположения элементов некоторого конечного множества в соответствии с заданными правилами, т.е. комбинаторика решает задачи выбора элементов из конечного множества и размещения этих элементов в каком-либо порядке.
Размещениями из n – элементов по m – элементов ( 

Пример № 1. Сколько трехзначных чисел можно составить из цифр от 1…9?


Перестановками из n – элементов называется число размещений из этих n – элементов по n – элементов.

Пример № 2. Сколькими способами можно расставить 5 книг на полке?

Сочетаниями из n – элементов по m – элементов называются комбинации составленные из данных n – элементов по m – элементов, которые отличаются друг от друга хотя бы одним элементом.
Пример № 3. В группе 30 студентов. Для сдачи зачета их необходимо разбить на три группы. Сколькими способами это можно сделать?
1. Обозначьте цели комбинаторики.
2. Что называется числом сочетаний из n элементов по m?
3. Что называется числом размещений из n элементов по m?
4. Что называется перестановкой из n элементов?
1. Сколькими способами можно в группе из 25 человек направить 4 студента на научно – практическую конференцию?
2. Десять студентов обменялись рукопожатиями. Сколько было рукопожатий?
3. Сколькими способами можно составить трехцветный полосатый флаг из семи различных по цвету отрезов материи?
4. Сколько словарей надо издать, чтобы можно было выполнять переводы с любого из пяти языков на любой из них?
5. Вычислите:
6. Вычислите:
8. Найдите число размещений из 10 элементов по 4.
9. Вычислите:
10. Тридцать студентов обменялись фотокарточками. Сколько всего было фотокарточек?
11. Сколькими способами можно из восьми кандидатов можно выбрать три лица на три должности?
12. Решите уравнение:
13. Вычислите значение выражения:
14. Вычислите значение выражения:
15. Сколькими способами можно составить список из десяти человек?
1. Математика: учебник для учреждений нач. и сред. проф. образования / М.И. Башмаков. –М.: Издательский центр «Академия», 2010 г.
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок № 8 Перпендикулярность прямой и плоскости
Перечень вопросов, рассматриваемых по теме
Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости
Теорема о прямой перпендикулярной к плоскости. Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл. Базовый и профильный уровень. М.: Просвещение, 2015. С.1-10.
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 9 класса. Базовый и профильный уровень
Зив Б.Г. Геометрия. Дидактические материалы. 10-11 класс М.: Просвещение, 2015.
Открытые электронные ресурсы:
Перпендикулярность прямой и плоскости. http://school-collection.edu.ru // Единая коллекция цифровых образовательных ресурсов.
Перпендикулярность прямой и плоскости. https://www.yaklass.ru // Я-класс. Образовательный портал Сколково.
Теоретический материал для самостоятельного изучения
Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой..
Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
Проведем какую-нибудь прямую x в плоскости α, т.е. x ∊ α.Так как а ⊥ α, то а ⊥ x.
По лемме о перпендикулярности двух параллельных прямых к третьей а1 ⊥ x.
Таким образом, прямая а1 перпендикулярна к любой прямой, лежащей в плоскости α, т. е. а1 ⊥ α
Теорема. Ели две прямые перпендикулярны плоскости, то они параллельны.
Через какую-нибудь точку М прямой b проведем прямую b1, параллельную прямой а.
Докажем, что прямая b1 совпадает с прямой b. Тем самым будем доказано, что а ‖ b. Допустим, что прямые b1 и b не совпадают. Тогда в плоскости β, содержащей прямые b и b1, через точку М проходят две прямые, перпендикулярные к прямой с, по которой пересекаются плоскости α и β. Но это невозможно, следовательно, а ‖ b, т.е. b ∊ β, b1 ∊ β, α 
Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.
Теорема. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Пусть дана плоскость α и точка М (см. рис. 2). Нужно доказать, что через точку М проходит единственная прямая с, перпендикулярная плоскости α.
Проведем прямую а в плоскости α (см. рис. 3). Согласно доказанному выше утверждению, через точку М можно провести плоскость γ перпендикулярную прямой а. Пусть прямая b – линия пересечения плоскостей α и γ.
В плоскости γ через точку М проведем прямую с, перпендикулярную прямой b.
Прямая с перпендикулярна b по построению, прямая с перпендикулярна а (так как прямая а перпендикулярна плоскости γ, а значит, и прямой с, лежащей в плоскости γ). Получаем, что прямая с перпендикулярна двум пересекающимся прямым из плоскости α. Значит, по признаку перпендикулярности прямой и плоскости, прямая с перпендикулярна плоскости α. Докажем, что такая прямая с единственная.
Предположим, что существует прямая с1, проходящая через точку М и перпендикулярная плоскости α. Получаем, что прямые с и с1 перпендикулярны плоскости α. Значит, прямые с и с1 параллельны. Но по построению прямые с и с1пересекаются в точке М. Получили противоречие. Значит, существует единственная прямая, проходящая через точку М и перпендикулярная плоскости α, что и требовалось доказать.
Теоретический материал для углубленного изучения
Теорема о прямой перпендикулярной к плоскости. Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.
Доказательство (см. рис. 1)
Пусть нам дана прямая а и точка М. Докажем, что существует плоскость γ, которая проходит через точку М и которая перпендикулярна прямой а.
Через прямую а проведем плоскости α и β так, что точка М принадлежит плоскости α. Плоскости α и β пересекаются по прямой а. В плоскости α через точку М проведем перпендикуляр MN (или р) к прямой а, 
Примеры и разборы решения заданий тренировочного модуля
Выбор элемента из выпадающего списка
Выпишите ребра, перпендикулярные плоскости (DC
Правильный вариант/варианты (или правильные комбинации вариантов):
Неправильный вариант/варианты (или комбинации):
Подсказка: в кубе все углы по 


Закончите предложение, чтобы получилось верное утверждение.
Правильный вариант/варианты (или правильные комбинации вариантов):
Две прямые называются перпендикулярными, если …
угол между ними равен 90
Если плоскость перпендикулярна одной из двух параллельных прямых, то она …
перпендикулярна и другой
Неправильный вариант/варианты (или комбинации):
Лемма: Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к третьей прямой.
Теорема: если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
Докажите что две прямые перпендикулярные одной и той же плоскости параллельны
Углы бывают острые, прямые и тупые.
Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым.
Два угла с одной общей стороной называются смежными.
На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.
Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°
При пересечении двух прямых образуются четыре угла:
Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.
∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:
∡1 + ∡2 = 180°
∡1 + ∡4 = 180°
∡2 = ∡4
То же справедливо и для ∡1 и ∡3.
Прямые, пересекающиеся под прямым углом, называются перпендикулярными.
∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.
Перпендикулярность прямых принято обозначать так: a⟂b
Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда»! По промокоду GEOM72021 вы получите неделю бесплатного доступа к курсу геометрии 7 класса, в котором изучаются перпендикулярные прямые!
Теорема о перпендикулярных прямых
Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.
Построим доказательство теоремы о перпендикулярных прямых «от противного», то есть для начала предположим, что утверждение неверно.
Возьмём прямую a, отметим на ней точки О и B. От луча OB отложим ∡BOA = 90°. Таким образом, отрезок OA будет находиться на прямой, перпендикулярной а.
Теперь предположим, что в той же полуплоскости существует другой перпендикуляр к а, проходящий через О. Назовём его OK. ∡BOK и ∡BOA, равны 90° и лежат в одной полуплоскости относительно луча OB. Но от луча OB в данной полуплоскости можно отложить только один прямой угол. Поэтому другой прямой, проходящей через О и перпендикулярной a, не существует. Теорема доказана.
Свойство перпендикулярных прямых
Две прямые, перпендикулярные третьей, не пересекаются.
Пусть a⟂b и a⟂c. b и с не пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.
У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Интересное по рубрике
Найдите необходимую статью по тегам
Подпишитесь на нашу рассылку
Мы в инстаграм
Домашняя онлайн-школа
Помогаем ученикам 5–11 классов получать качественные знания в любой точке мира, совмещать учёбу со спортом и творчеством

Рекомендуем прочитать
Реальный опыт семейного обучения
Звонок по России бесплатный
Посмотреть на карте
Если вы не нашли ответ на свой вопрос на нашем сайте, включая раздел «Вопросы и ответы», закажите обратный звонок. Мы скоро свяжемся с вами.






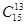














.jpg)

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)










