Докажите что единицей измерения ускорения в международной системе единиц является
Единицы измерения ускорения.
Ускорение – это физическая величина (a, от лат. acceleratio), характеризующая быстроту изменения скорости тела. Ускорение является векторной величиной, показывающей, насколько изменяется вектор скорости 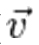
Рассмотрим движение автомобиля. Трогаясь с места, он увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус.
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
Направление ускорения также совпадает с направлением изменения скорости Δ 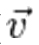
Равнопеременное движение точки – это движение с постоянным ускорением,
Под словом равнопеременное понимают:
2. Равнозамедленное движение – если модуль скорости уменьшается, т.е. ускорение антипараллельно скорости: 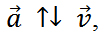
Поскольку ускорение равнопеременного движения постоянно, оно равно изменению скорости за любой конечный интервал времени:
где 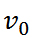
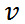

Если же нулю равна не начальная, а конечная скорость ( 
При движении по криволинейной траектории изменяется не только модуль скорости, но и ее направление. В этом случае вектор ускорения представляют в виде двух составляющих: тангенциальной – по касательной к траектории движения, и нормальной – перпендикулярно траектории
В соответствии с этим проекцию ускорения 
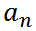
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Направление вектора тангенциального ускорения 
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть, вектор нормального ускорения перпендикулярен линейной скорости движения. Нормальное ускорение характеризует изменение скорости по направлению. Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

Что такое ускорение?
Ускорение — физическая векторная величина, которая характеризует насколько быстро тело (материальная точка) изменяет скорость своего движения. Ускорение является важной кинематической характеристикой материальной точки.
Самый простой вид движения — равномерное движение по прямой линии, когда скорость тела постоянна и тело за любые равные промежутки времени проходит одинаковый путь.
Но большинство движений неравномерны. На одних участках скорость тела больше, на других меньше. Машина начиная движение двигается все быстрее. а останавливаясь замедляется.
Если скорость тела при неравномерном движении за любые равные промежутки времени изменяется одинаково, то движение называют равноускоренным.
Как и скорость, ускорение тела характеризуется не только числовым значением, но и направлением. Это означает, что ускорение тоже является векторной величиной. Поэтому на рисунках его изображают в виде стрелки.
Единицей ускорения в СИ является такое ускорение, при котором за каждую секунду скорость тела изменяется на 1 м/с, т. е. метр в секунду за секунду. Эту единицу обозначают 1 м/с2 и называют «метр на секунду в квадрате».
Как и скорость, ускорение тела характеризуется не только числовым значением, но и направлением. Это означает, что ускорение тоже является векторной величиной. Поэтому на рисунках его изображают в виде стрелки.
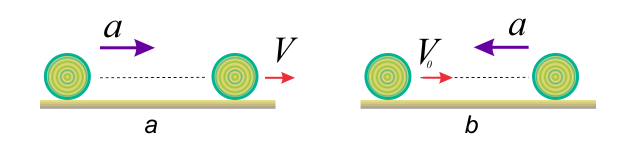
Если скорость тела при равноускоренном прямолинейном движении возрастает, то ускорение направлено в ту же сторону, что и скорость (рис. а); если же скорость тела при данном движении уменьшается, то ускорение направлено в противоположную сторону (рис. б).
Среднее и мгновенное ускорение
Среднее ускорение материальной точки на некотором промежутке времени — это отношение изменения его скорости, что произошло за это время, к продолжительности этого промежутка:
Тангенциальное и нормальное ускорение
\( = \dfrac
где \( \theta \) — угол между вектором скорости и осью абсцисс; \( \hat n \) — орт перпендикуляра к скорости.
где \( \vec a_ <\tau>= \dfrac
Учитывая, что вектор скорости направлен по касательной к траектории движения, то \( \hat n \) — это орт нормали к траектории движения, который направлен к центру кривизны траектории. Таким образом, нормальное ускорение направлено к центру кривизны траектории, в то время как тангенциальное — по касательной к ней. Тангенциальное ускорение характеризует скорость изменения величины скорости, в то время как нормальное характеризует скорость изменения ее направления.
\( a_
Измерение ускорения
Ускорение измеряется в метрах (разделенных) на секунду во второй степени (м/с 2 ). Величина ускорения определяет, насколько изменится скорость тела за единицу времени, если оно будет постоянно двигаться с таким ускорением. Например, тело, движущееся с ускорением 1 м/с 2 за каждую секунду изменяет свою скорость на 1 м/с.
Единица измерения ускорения
Единица измерения ускорения в Международной системе единиц
Из определения (1) следует, что ускорение имеет единицу измерения:
Единицы измерения ускорения, не относящиеся к системе СИ
Гал (иногда галилео) был назван в честь Г. Галилея. Чаще всего гал используют в гравиметрии при обозначении единиц ускорения свободного падения. Так, стандартная величина ускорения свободного падения составляет:
В Британских системах единиц встречается единица измерения ускорения фут, деленный на секунду в квадрате:
Примеры задач с решением
Решение. Центростремительное ускорение можно найти, если использовать формулу:
Подставим правую часть выражения (1.3) вместо радиуса в (1.1), имеем:
Проверим размерность правой части выражения (1.4):
\[\left[a_n\right]=\left[\nu v\right]=\left[\nu \right]\left[v\right]=\frac<1><с>\cdot \frac<м><с>=\frac<м><с^2>.\]
\[a_n=2\cdot 3,14\cdot 8\cdot 20=1004,8\ \left(\frac<м><с^2>\right).\]
Задание. Каким будет ускорение свободного падения, для тела, которое находится на высоте равной радиусу Земли? Выразите ускорение свободного падения в единицах гал.
Решение. Сделаем рисунок.
На тело А (рис.1) действует сила гравитации Земли, равная:
В соответствии со вторым законом Ньютона имеем:
Из формулы (2.2) имеем:
Что такое ускорение?
Ускорение — физическая векторная величина, которая характеризует насколько быстро тело (материальная точка) изменяет скорость своего движения. Ускорение является важной кинематической характеристикой материальной точки.
Самый простой вид движения — равномерное движение по прямой линии, когда скорость тела постоянна и тело за любые равные промежутки времени проходит одинаковый путь.
Но большинство движений неравномерны. На одних участках скорость тела больше, на других меньше. Машина начиная движение двигается все быстрее. а останавливаясь замедляется.
Если скорость тела при неравномерном движении за любые равные промежутки времени изменяется одинаково, то движение называют равноускоренным.
Как и скорость, ускорение тела характеризуется не только числовым значением, но и направлением. Это означает, что ускорение тоже является векторной величиной. Поэтому на рисунках его изображают в виде стрелки.
Единицей ускорения в СИ является такое ускорение, при котором за каждую секунду скорость тела изменяется на 1 м/с, т. е. метр в секунду за секунду. Эту единицу обозначают 1 м/с2 и называют «метр на секунду в квадрате».
Как и скорость, ускорение тела характеризуется не только числовым значением, но и направлением. Это означает, что ускорение тоже является векторной величиной. Поэтому на рисунках его изображают в виде стрелки.
Если скорость тела при равноускоренном прямолинейном движении возрастает, то ускорение направлено в ту же сторону, что и скорость (рис. а); если же скорость тела при данном движении уменьшается, то ускорение направлено в противоположную сторону (рис. б).
Среднее и мгновенное ускорение
Среднее ускорение материальной точки на некотором промежутке времени — это отношение изменения его скорости, что произошло за это время, к продолжительности этого промежутка:
Тангенциальное и нормальное ускорение
\( = \dfrac
где \( \theta \) — угол между вектором скорости и осью абсцисс; \( \hat n \) — орт перпендикуляра к скорости.
где \( \vec a_ <\tau>= \dfrac
Учитывая, что вектор скорости направлен по касательной к траектории движения, то \( \hat n \) — это орт нормали к траектории движения, который направлен к центру кривизны траектории. Таким образом, нормальное ускорение направлено к центру кривизны траектории, в то время как тангенциальное — по касательной к ней. Тангенциальное ускорение характеризует скорость изменения величины скорости, в то время как нормальное характеризует скорость изменения ее направления.
\( a_
Измерение ускорения
Ускорение измеряется в метрах (разделенных) на секунду во второй степени (м/с 2 ). Величина ускорения определяет, насколько изменится скорость тела за единицу времени, если оно будет постоянно двигаться с таким ускорением. Например, тело, движущееся с ускорением 1 м/с 2 за каждую секунду изменяет свою скорость на 1 м/с.
Ускорение
Ускоре́ние (обычно обозначается 

Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².
Производная ускорения по времени, то есть величина, характеризующая скорость изменения ускорения, называется рывок:





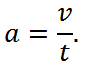
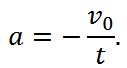

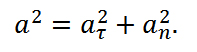
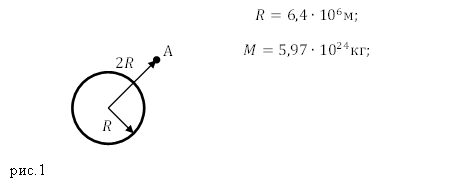


 .
.
 .
.
 — начальная скорость тела,
— начальная скорость тела,  — конечная скорость тела;
— конечная скорость тела;  — ускорение тела;
— ускорение тела;  — пройденный телом путь.
— пройденный телом путь.

 направлено по касательной к траектории (обозначается иногда
направлено по касательной к траектории (обозначается иногда  и т. д., в зависимости от того, какой буквой в данной книге принято обозначать ускорение). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.
и т. д., в зависимости от того, какой буквой в данной книге принято обозначать ускорение). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.
 — возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) (также обозначается иногда
— возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) (также обозначается иногда 


 :
: ,
, , называемое бинормальным ускорением, всегда равно нулю. Это можно считать прямым следствием определения векторов
, называемое бинормальным ускорением, всегда равно нулю. Это можно считать прямым следствием определения векторов  : можно сказать, что они выбираются именно так, чтобы первый всегда совпадал с нормальным ускорением, второй же ортогонально первому.
: можно сказать, что они выбираются именно так, чтобы первый всегда совпадал с нормальным ускорением, второй же ортогонально первому. и
и  называются касательным (тангенциальным) и нормальным ускорениями соответственно.
называются касательным (тангенциальным) и нормальным ускорениями соответственно. ,
, ,
, — вектор угловой скорости тела, а
— вектор угловой скорости тела, а  — вектор углового ускорения тела.
— вектор углового ускорения тела. .
.
