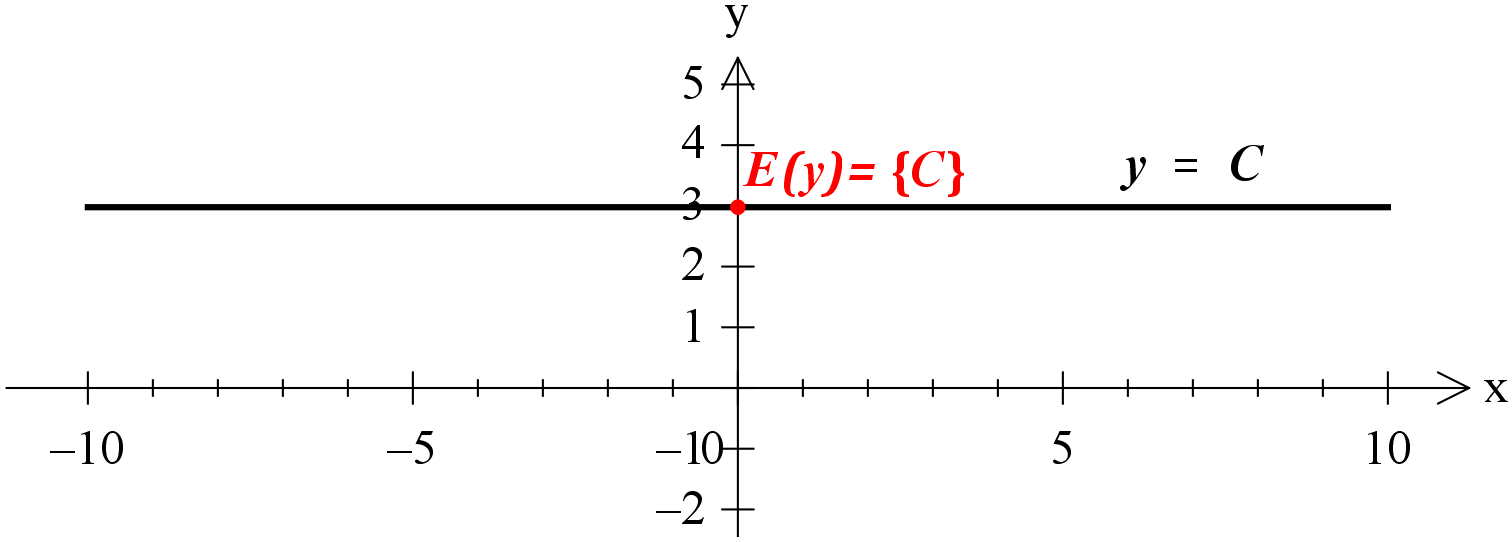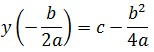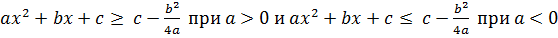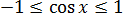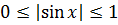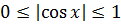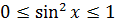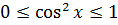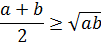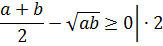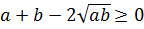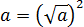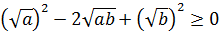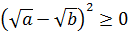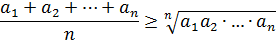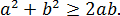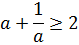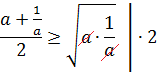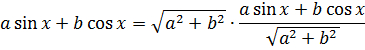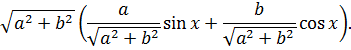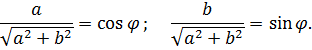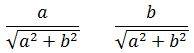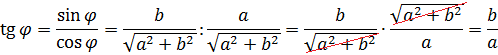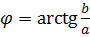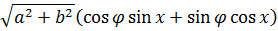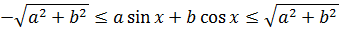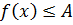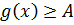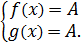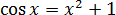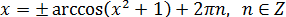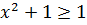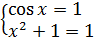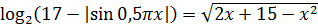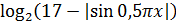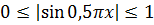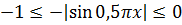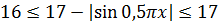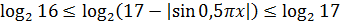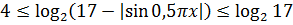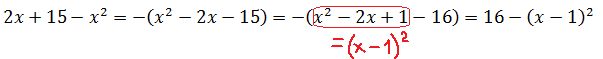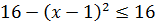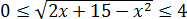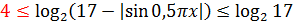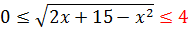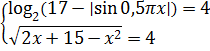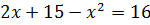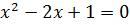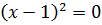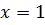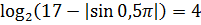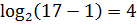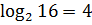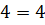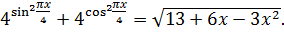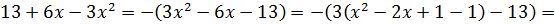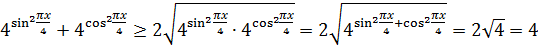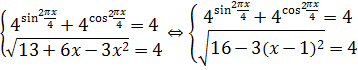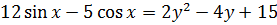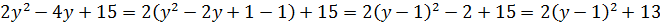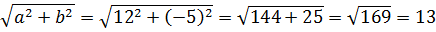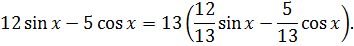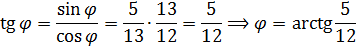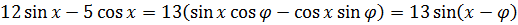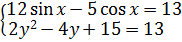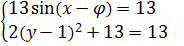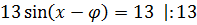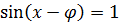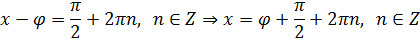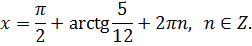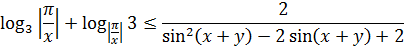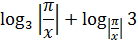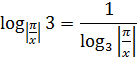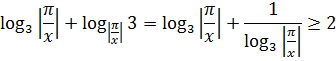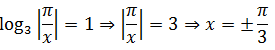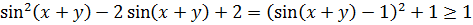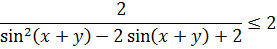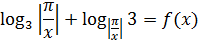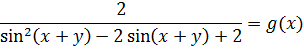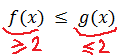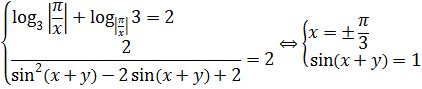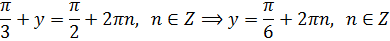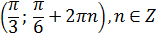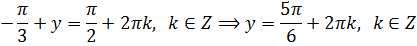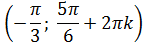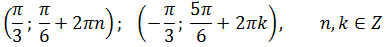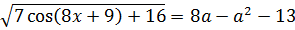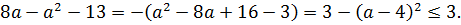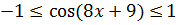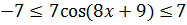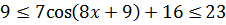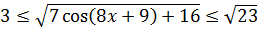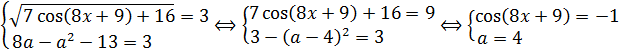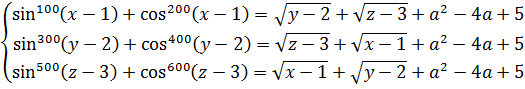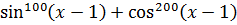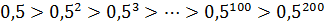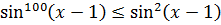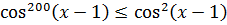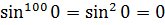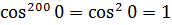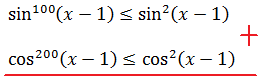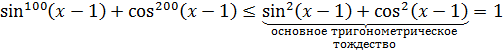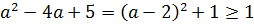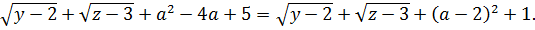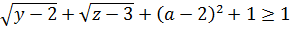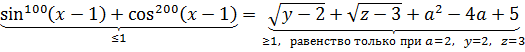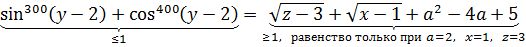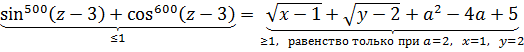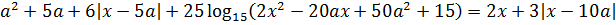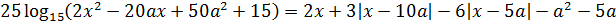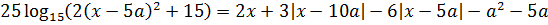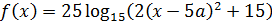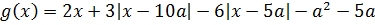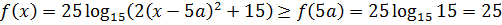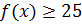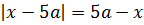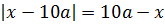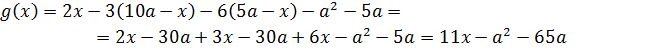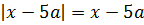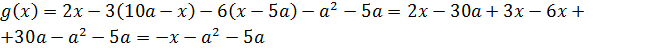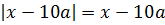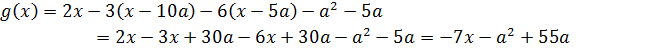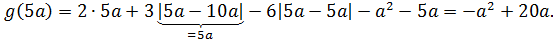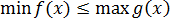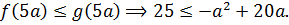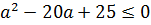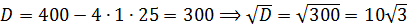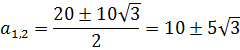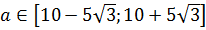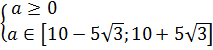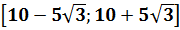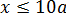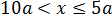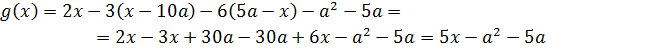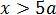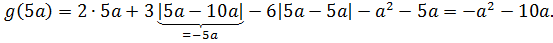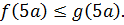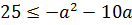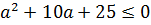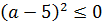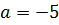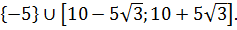Докажите что функция y модуль x

Ограниченность (или метод оценок)

Аналитические способы решения задач с параметрами. Ограниченность. Метод оценок.

Ещё один распространённый метод аналитического решения задач с параметрами — это метод оценок. Или по-другому — метод мажорант. Основывается он на таком важном свойстве многих функций, как ограниченность. Для начала пробежимся по самому понятию ограниченности.

Что такое ограниченность? Ограниченные функции.

То что это слово происходит от слова «граница», вопросов, думаю, ни у кого не вызывает.) Многое в нашем окружении обладает ограниченностью: сутки ограничены 24 часами, проезжая часть дороги ограничена тротуаром или обочиной, секретная территория ограничена забором с колючей проволокой. 🙂 А в математике бывают ограниченные функции.

Что же такое ограниченная функция? Это функция, область значений которой ограничена каким-то числом (или двумя числами). Что такое область значений функции? Это те значения, которые может принимать функция в принципе. Обозначается она, как мы помним, E(y).

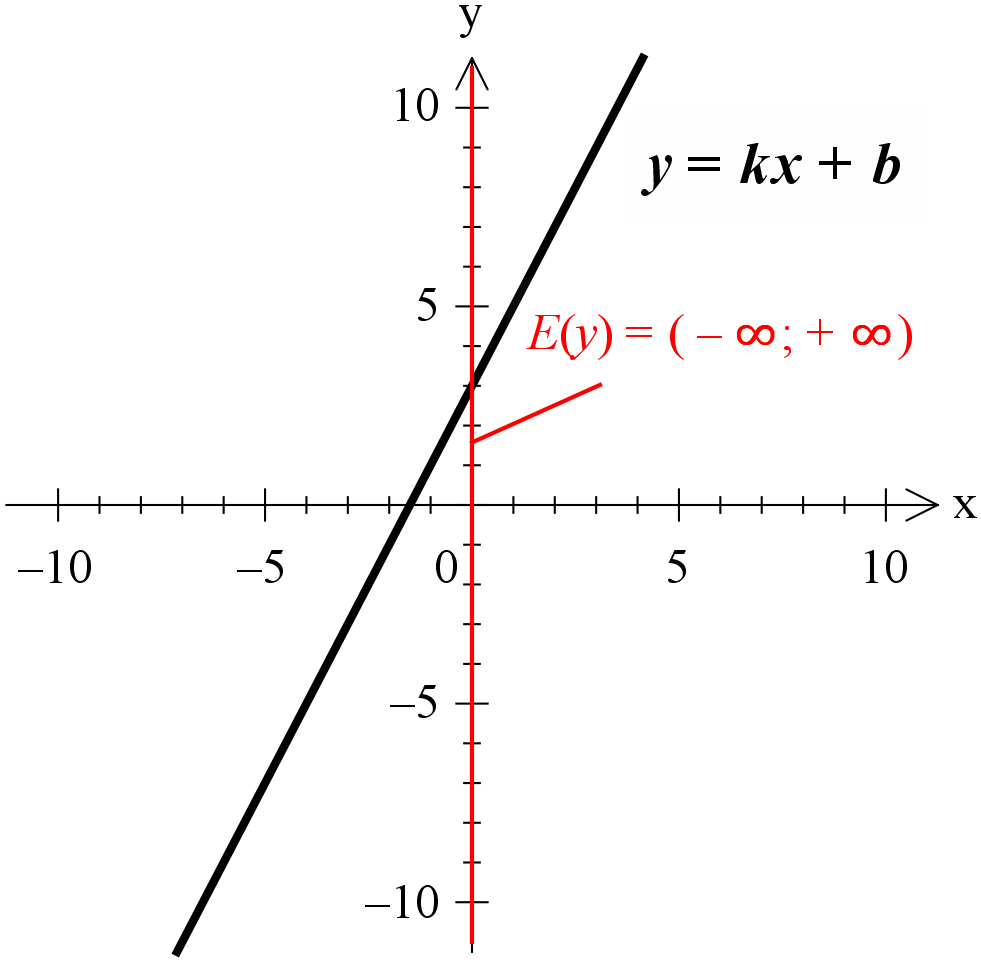
Например, для линейной функции y = kx+b областью значений будет вся числовая прямая:

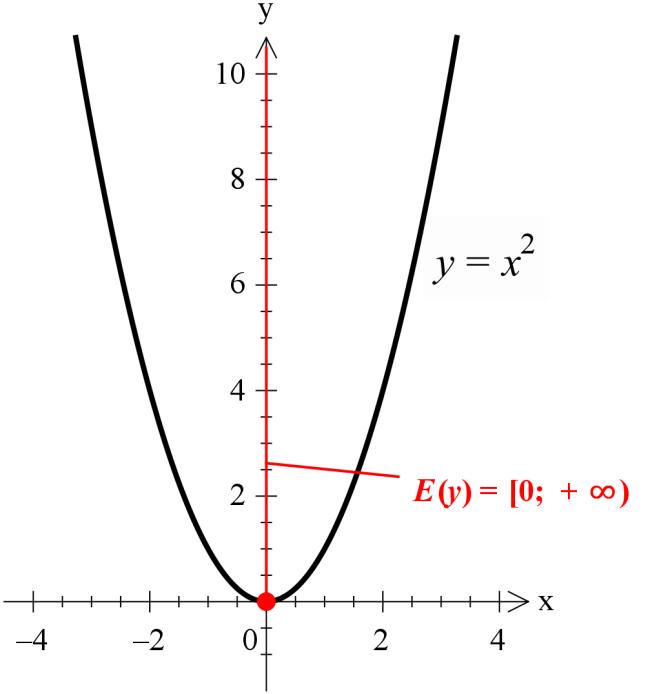
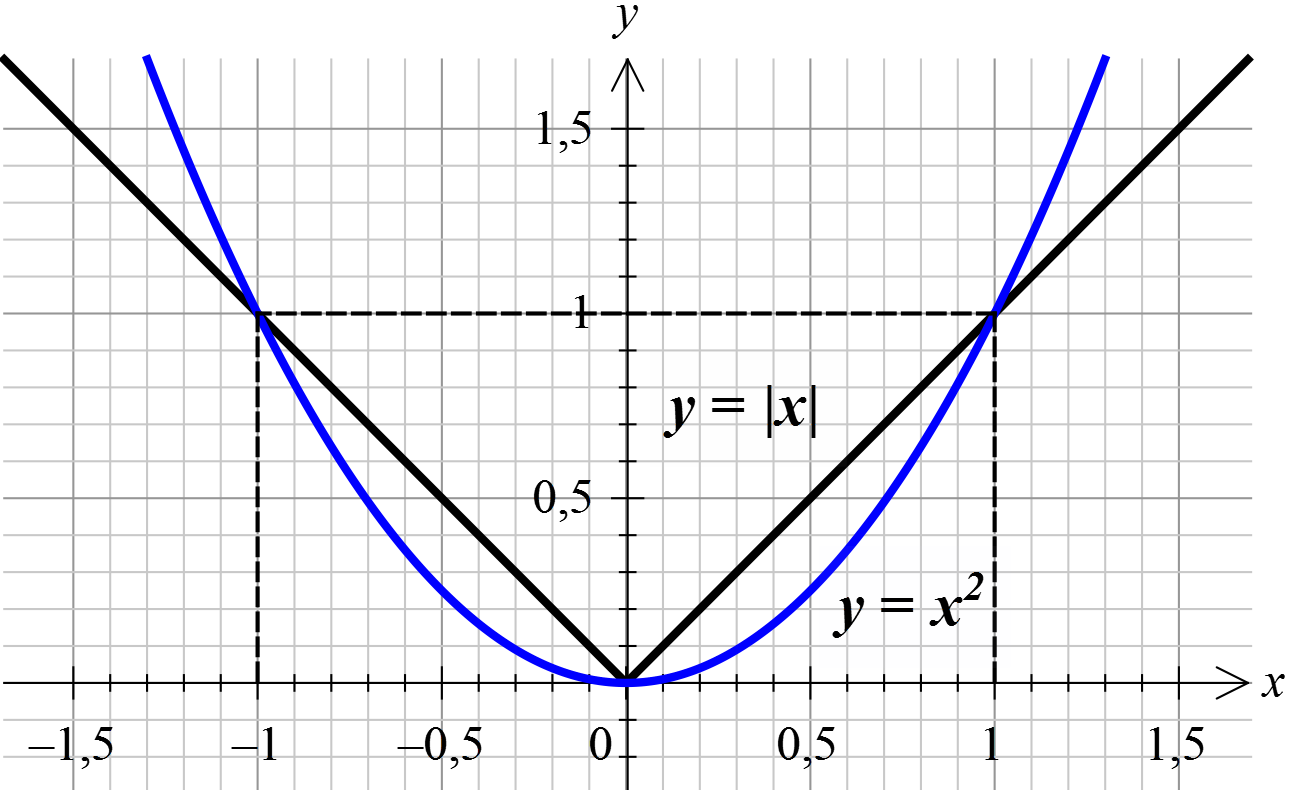
Для параболы y = x 2 областью значений будет множество всех неотрицательных чисел:

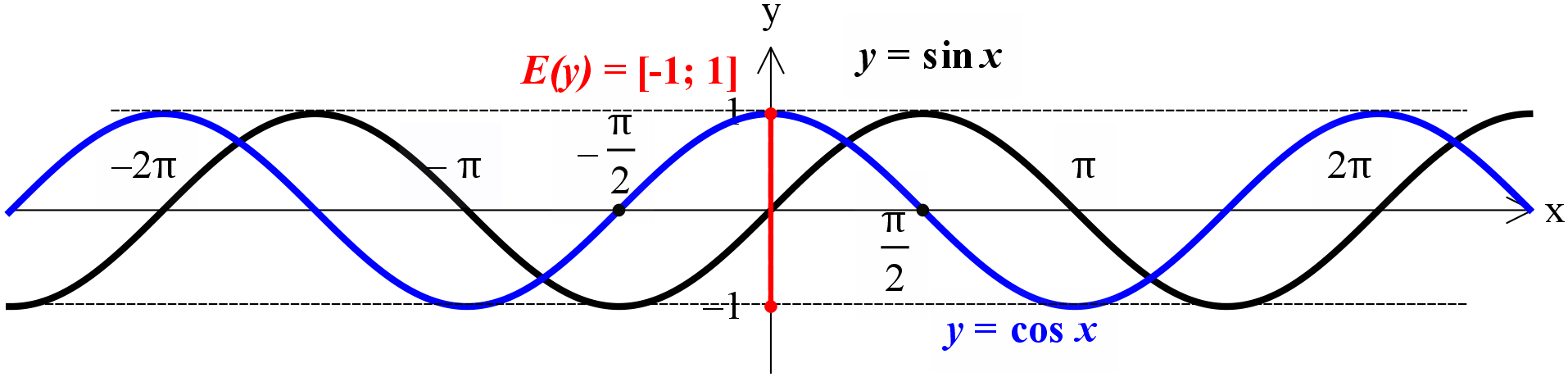
Для синуса или косинуса областью значений служит отрезок [-1; 1]. То есть, E(y) = [-1; 1].

Для константы y = C область значений вообще состоит всего лишь из одной точки: E(y) = .

Одних только этих примеров уже достаточно, чтобы понять, что бывают функции, графики которых неограниченно простираются сверху вниз (или снизу вверх), либо которые ограничены только сверху (снизу), либо которые «зажаты» между какими-то двумя числами. А также константы.

Например, сверху ограничена любая квадратичная функция y = ax 2 +bx+c с отрицательным коэффициентом «a» (то есть, с параболой ветвями вниз). Каким же именно числом? Значением в вершинке:

Например, наши любимые парабола y = x 2 и модуль y = |x| ограничены снизу числом 0.

А вот функция, ограниченная как сверху, так и снизу, называется просто ограниченная функция. Например, любой синус и любой косинус ограничены числами 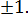Арктангенс ограничен числами ± π /2. Константа, ясен перец, ограничена сама собой же.)

И так далее. Что такое ограниченность и какие у неё бывают разновидности, в общих чертах теперь, думаю, понятно. ) Мы не будем здесь углубляться в густые дебри теории множеств, заикаться про точную верхнюю и нижнюю грани (называемые красивыми словами «супремум» и «инфимум»), ибо для решения нестандартных задач (с параметрами и без) приведённой выше информации про ограниченность вполне достаточно.)

А теперь составим небольшой список наиболее часто встречающихся ограниченных конструкций.

Квадратный трёхчлен

Любой квадратный трёхчлен ограничен сверху (снизу) значением в вершине соответствующей параболы:

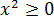
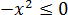
В частности, и .

Модуль

Любой модуль всегда неотрицателен: |x| ≥ 0.

Синус и косинус

и

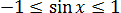
Обратные тригонометрические функции

π /2 ≤ arcsin x ≤ π /2 0 ≤ arccos x ≤ π

π /2 arctg x π /2 0 arcctg x π

Полезные неравенства

Что ещё очень часто применяется при решении задач с использованием метода оценок, так это некоторые весьма и весьма нетривиальные, но очень полезные неравенства. Сейчас мы их выпишем и разберём (в том числе и докажем).

Неравенство о среднем арифметическом и среднем геометрическом (неравенство Коши)

Первое полезное неравенство, которое мы рассмотрим, — это неравенство, связывающее среднее арифметическое и среднее геометрическое двух чисел. Называется оно неравенством Коши и выглядит так:

А по-русски это неравенство звучит так: « Среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического. »

Здесь есть ограничение: оба числа должны быть неотрицательными. Иначе либо корень справа вообще потеряет смысл, либо неравенство будет неверно.

Доказывается оно довольно просто. Для этого перенесём 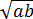влево и умножим обе части на 2:

Из свойств корней мы знаем, что:

.

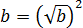
Если теперь вставить эти выражения в наше неравенство, то слева получится полный квадрат разности:

Последнее неравенство возражений, думаю, не вызывает: квадрат любого выражения всегда неотрицателен. 🙂 Тем самым, неравенство Коши доказано.

Обратим внимание, что неравенство здесь нестрогое — больше, либо равно. А вот когда достигается это самое «равно»? Только в единственном случае — когда .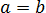

Кстати говоря, неравенство Коши справедливо не только для двух, а для любого количества чисел. В более общей форме оно записывается вот так:

Важное следствие из неравенства Коши:

Сумма двух взаимно обратных величин

Следующее неравенство, на которое мы обратим внимание, — это сумма двух положительных взаимно обратных величин. При a > 0 справедливо вот такое неравенство:

Доказывается оно довольно легко с использованием предыдущего неравенства Коши.)

Положив в нём b=1/a, получим:

Что и требовалось доказать.)

Здесь неравенство снова нестрогое и превращается в равенство только при a = 1/a, то есть при a = 1.

Связь квадрата и модуля

Третья группа полезных неравенств — связь квадрата какой-то величины с модулем этой самой величины:

при

при

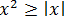
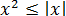
Оценка некоторых тригонометрических выражений

Итак, пусть у нас есть вот такое выражение с синусом и косинусом:

Здесь a и b – просто какие-то числа, одновременно не равные нулю. Нам теперь надо оценить это выражение. Для этого проделываем вот такую манипуляцию: умножаем и тут же делим всю конструкцию на вот такой корень :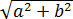

Казалось бы, что это ещё за выкрутасы такие? Ничего, сейчас интересно будет. 🙂 Теперь делим числитель почленно на этот самый корень:

А теперь — самое интересное! Вводим вот такие обозначения:

Правомерна ли такая замена? Проверим по основному тригонометрическому тождеству:

Итак, основное тригонометрическое тождество выполнено, а это значит, что наши загадочные числа

и впрямь есть косинус и синус некоторого угла 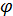. Этот новый угол «фи» и называется тем самым вспомогательным углом. 🙂 Кстати, можно точно определить, чему равен этот самый угол «фи». Для этого поделим друг на друга его синус и косинус. Как мы знаем, это будет тангенс:

Что ж, перепишем наше выражение с учётом доказанных фактов:

А теперь — сворачиваем наше выражение по формуле синуса суммы двух углов. Вот так:

.

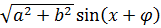
Любой синус, как нам известно, заключён в пределах [-1; 1], а это значит, что всё наше выражение 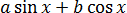заключено вот в таких пределах:

Это неравенство довольно часто применяется при оценке тригонометрических выражений. Полезно запомнить.)

Принцип оценки левой и правой части (или принцип разделяющего числа)

И, наконец, последнее что мы рассмотрим — это вот такую типичную ситуацию. Пусть у нас имеется уравнение f(x) = g(x). Допустим, мы каким-то образом установили, что левая часть не больше какого-то числа А:

Также мы установили, что правая часть не меньше этого же числа:

Или всё наоборот — не суть важно. Важно другое — одна из функций ограничена сверху числом А, а вторая функция ограничена снизу этим же самым числом.) Когда возможно равенство левой и правой части? Да! Когда одновременно и левая, и правая части равны этому граничному числу А!

То есть, наше исходное уравнение f(x) = g(x) будет равносильно вот такой системе:

Решается такая системка, как правило, уже без особого труда.

Этот метод часто применяется в той ситуации, когда слева и справа стоят функции разной природы. Скажем, синус и многочлен. Или косинус и логарифм… Это намёк.) Попробуйте оценить левую и правую части! В 99% случаев помогает!

Теперь кратко о задачах, которые будут рассматриваться в настоящем материале. Большинство из этих задач НЕ решаются стандартными способами — сведением к простейшим уравнениям или неравенствам, разложением на множители, возведением в квадрат и подобными преобразованиями. Однако, если попытаться оценить конструкции, входящие в задачу, как дорога к ответу становится простой, понятной и красивой, а задача из монстра становится белой и пушистой.) «Внешний вид» задач, где явно напрашивается метод оценок, примерно следующий:

— наличие слева и справа «разнородных» функций (синуса и логарифма, косинуса и квадратного трёхчлена и т.п.);

— присутствие ограниченных конструкций (синусов/косинусов, квадратных трёхчленов, модулей, суммы взаимно обратных величин и т.д.).

Распознавать такие задачи после некоторой тренировки труда не составит. Если тренироваться, конечно. 🙂

Уравнения (неравенства) без параметра, решаемые методом оценок

Что ж, хватит грузной теории, перейдём теперь к конкретным задачам и посмотрим на метод оценок в действии. Для начала рассмотрим задачи без параметра, но с одной или несколькими неизвестными, а уже потом будем рассматривать конкретные параметрические задачи из вариантов ЕГЭ.

Начнём пока что с такого задания.

Пример 1

Решить уравнение:

Если мы сейчас начнём решать это уравнение по стандартным шаблонам и напишем какую-нибудь ересь типа

,

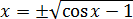
то погрязнем в вычислениях и выкладках, что называется, всерьёз и надолго. 🙂

Как же подступиться к этому уравнению? Путём недолгих размышлений, можно, конечно, догадаться, что число x = 0 является его корнем. А вдруг, кроме нуля, у него есть ещё корни? Так и будем гадать на кофейной гуще? Так как мы не гадалки, то попробуем применить обещанный метод мажорант или оценок.

Внешний вид уравнения (слева косинус, справа — многочлен) намекает на оценку левой и правой частей. Вот и попробуем оценить левую и правую части нашего злого уравнения.

А про квадрат мы также знаем, что он всегда неотрицателен:

А, стало быть, если к квадрату прибавить 1, то вся правая часть будет не меньше единички:

А теперь осмысливаем результат: левая часть не больше единицы, а правая часть — не меньше единицы. А это значит, что равенство обеих частей возможно только в единственном случае — когда обе части равны единице! И наше зверское уравнение превращается в эквивалентную систему:

Нетрудно убедиться, что единственным решением этой системки является x = 0. И, следовательно, других корней, кроме нуля, это уравнение не имеет. Вот это строгое обоснование того факта, что других корней нет.

Пример 2

Снова совершенно немыслимый набор функций: слева логарифм от какой-то белиберды с синусом, а справа — корень из квадратного трёхчлена.) Значит, стандартные приёмы (типа возведения в квадрат, ликвидации логарифмов) бесполезны. Значит, пример заточен под какой-то нестандартный ход. Какой? Слева и справа стоят функции совершенно разного рода — корень и логарифм. Такой внешний вид примера — своего рода сигнал к применению метода мажорант. Попробуем оценить обе части? 🙂

Итак, берём сначала логарифм

Значит, для синуса можно записать:

Если теперь это неравенство помножить на (-1), то получим:

Следующим шагом прибавляем 17 ко всем трём частям:

И, наконец, последнее усилие — берём логарифм по основанию 2. Так как в основании логарифма стоит двойка (т.е. число, большее 1), то знаки нашего двойного неравенства от логарифмирования не поменяются:

Вот так. Значит, вся конструкция слева заключена в отрезке [4; log₂17]. Иначе быть не может.

Теперь берёмся за правую часть, с корнем .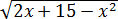

Квадратный трёхчлен следует оценивать, предварительно выделив полный квадрат. Вот так:

Зачем мы привели трёхчлен именно к такому виду? А затем, что теперь стало всё видно: если от 16 отнять что-то в квадрате (неотрицательное!), то это выражение будет в любом случае не больше 16:

Значит, если из этого выражения извлечь корень, то он точно будет не больше 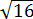, т.е. 4. Итак,

А нулём мы дополнительно ограничиваем просто в силу неотрицательности арифметического корня.)

А теперь — состыковываем результаты наших оценок левой и правой частей:

Теперь уже видно, что нашим разделяющим числом (т.е. мажорантой) является четвёрка: левая часть не меньше 4, а правая — не больше 4. А значит, для того чтобы наше уравнение имело корни, левая и правая части одновременно должны быть равны 4. Таким образом, наше злое уравнение равносильно вот такой системе:

А решение этой системы уже не представляет никаких трудностей. Из второго уравнения легко можно получить единственный корень x = 1:

(возводим обе части в квадрат)

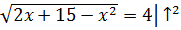
Проверим первое уравнение при x = 1:

Итак, единственным корнем уравнения является x = 1.

Идея ясна? Отлично! Тогда разбираем похожую задачку. Для тренировки.)

Пример 3

Ну, с корнем справа всё ясно. Его оцениваем с помощью выделения полного квадрата у подкоренного трёхчлена. 🙂 Полная аналогия с предыдущим примером:

.

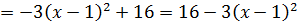
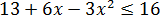
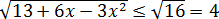
Тогда и, следовательно, .

Итак, правая часть не больше четвёрки. 🙂

А вот левую часть на этот раз будем оценивать с помощью неравенства Коши. Зря, что ли, мы его выводили? 🙂 Перепишем его ещё разочек, умножив обе части на 2:

.

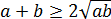
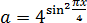
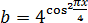
Если теперь положить в нём и , то 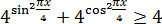получим следующее:

Итого , т.е. левая часть не меньше четвёрки.

И снова нашим разделяющим числом оказалась четвёрка. 🙂 То есть, всё наше уравнение равносильно системе:

Единственным решением этой системы (а значит, и исходного уравнения) является x=1.

Разберём теперь уравнение с двумя переменными. Казалось бы, всё гораздо сложнее, однако внешность обманчива. Если уметь грамотно проводить оценку. 🙂

Пример 4

Найти все пары чисел (x; y), удовлетворяющих уравнению:

Уравнение одно, а переменных две — икс и игрек. Как тут не испугаться… Однако, глаза боятся, а руки делают. 🙂 Оцениваем квадратный трёхчлен справа. Это нам уже знакомо:

А что можно сказать про левую часть ? Пока — ничего определённого. Но! Если присмотреться, то можно увидеть, что данное выражение — это конструкция вида . Метод вспомогательного угла нам в помощь! 🙂

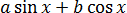
Первым делом считаем выражение

Число 13 здесь всплыло неспроста. 🙂 Ниже сами увидите. Итак, умножаем и делим наше выражение на 13:

А теперь — вводим новый угол 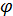вот с такими характеристиками: cos φ = 12/13; sin φ = 5/13.

Определим теперь сам угол. Через тангенс. 🙂

Значит, вся наша левая часть запишется вот так:

Стало быть, .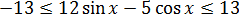

Без введения вспомогательного угла так красиво оценить левую часть вряд ли получилось бы. 🙂 Именно поэтому метод введения вспомогательного угла надо знать. В подобных задачах только он и спасает положение. Намёк понятен?)

Вот мы и вышли на разделяющее число. Тринадцать. Левая часть не больше тринадцати, а правая — не меньше тринадцати. Заменяем уравнение на равносильную систему:

Вспоминаем все наши преобразования:

Второе уравнение системы выполняется только при y = 1. А вот в первом уравнении, как и в обычном тригонометрическом, получается серия решений:

Решаем это простенькое тригонометрическое уравнение с синусом и получаем:

Вспомнив, что же такое это самое 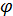, окончательно получим:

Получили бесконечную серию пар (x; y).

Ответ: ( π /2+arctg5/12+2 π n; 1 ), n ∊ Z

Итак, с уравнениями потренировались, рассмотрим теперь и что-нибудь из неравенств. Для неравенств применение метода мажорант полностью совпадает с таковым для уравнений. 🙂 Например, такое задание.

Пример 5

Внешний вид неравенства (слева логарифмы, справа — синусы) явно намекает на метод мажорант. Начнём с оценки левой части.

По одному очень хорошему свойству логарифмов, можно перевернуть второй из них:

Получили сумму двух взаимно обратных величин. Которая, как мы помним из нашей сводки, не меньше двойки. Вот и это неравенство нам тоже пригодилось! 🙂 Вперёд! Оцениваем:

Причём равенство достигается только при

Оба этих числа входят в ОДЗ нашего выражения слева.

Что же касается правой части, то в знаменателе нашей дроби сидит самый обычный квадратный трёхчлен. Только относительно синуса. 🙂 Всё как обычно, выделяем полный квадрат и оцениваем:

Раз знаменатель дроби не меньше единицы, то вся дробь не больше двойки:

Причём равенство этой дроби двойке достигается только когда её знаменатель равен единице, т.е. (sin(x+y)-1) 2 +1 = 1 или sin(x+y) = 1.

А теперь состыковываем результаты наших оценок. Для простоты как-нибудь обозначим наши функции:

, .

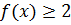
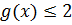
При этом у нас есть вот такое нестрогое неравенство:

Левая функция должна быть не больше правой. Но при этом левая функция находится выше двойки (либо равна), а правая — ниже двойки (либо равна). Как вы думаете, когда такое неравенство может выполняться? Ну, конечно! Только в одном единственном случае — когда обе части будут равны двойке! Иными словами, наше нестрогое неравенство может выполняется только в случае равенства. Бывает.)

Итак, заменяем всё наше страшное неравенство уже привычной нам системой:

Случай 1 ( х = π /3 )

​

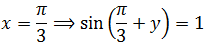
Получили первую пачку решений:

Разбираем второй случай:

Вторая пачка решений:

Как видите, когда разделяющее число (мажоранта) найдено, то дальнейшее решение труда в таких задачах, как правило, уже не составляет. Вопрос — а как искать такое число? К сожалению, универсального секретного заклинания на все случаи жизни здесь дать нельзя, но я надеюсь, что знание тех неравенств, что я привёл в самом начале урока, резко повысит ваши шансы на успех. Ну и плюс практика и опыт. Без них в сложных нестандартных задачах делать нечего. Увы.

Что ж, перейдём теперь к задачам с параметрами. В том числе и из ЕГЭ.

Задачи с параметрами на ограниченность.

Начнём пока с относительно несложной задачки с тригонометрией.

Пример 6

Найдите все значения параметра a , при каждом из которых уравнение

имеет хотя бы один корень.

Прежде всего, оцениваем квадратный трёхчлен справа. Это мы уже давно умеем:

Правая часть не превосходит тройки. Отлично! Берёмся теперь за корень. С ним тоже никаких проблем. Распутывать начинаем, разумеется, с косинуса:

Итак, наш корень не меньше тройки. А трёхчлен — не больше. Прекрасно! Это значит, что всё наше уравнение может иметь корни только при условии равенства обеих частей этой самой тройке:

Очевидно, первое уравнение нашей системы корни имеет. 🙂 Находить нам их не надо. )

Итак, единственное допустимое значение параметра — это a = 4. При прочих значениях « a » корней у уравнения не будет.

Теперь рассмотрим систему.

Пример 7

Найдите все значения параметра a , при каждом из которых система уравнений

Не пугаемся огромных степеней! На самом деле, это сделано как раз для того, чтобы запугать решающего. Не более.) Но мы же не будем поддаваться на такие глупые уловки, правда? 🙂

Запоминаем такую простую вещь. Если в задаче тусуются синусы и косинусы в очень больших степенях, то в 99% случаев срабатывает самая обыкновенная оценка синуса и косинуса по модулю, и огромные степени в таких задачах сводятся к обычным квадратам и (очень часто!) основному тригонометрическому тождеству, после чего дальнейшее решение становится очень простым и понятным. Посмотрим, как это работает на примере нашей страшной, на первый взгляд, системы.

Берём, например, левую часть первого уравнения:

Мы знаем, что синус и косинус всегда заключены в отрезке [-1; 1]. Иными словами, это какие-то дробные числа, по модулю меньшие (либо равные) единице. А теперь подумаем: чем больше степень такого числа, тем меньше по модулю будет результат. Возьмём для конкретики, например, число 0,5. Тогда будет справедлива такая цепочка неравенств:

То же самое будет и с любым синусом или косинусом. Это значит, что

Теперь сложим почленно эти два неравенства:

Это значит, что левая часть не больше единички.

Та же самая оценка левой части будет справедлива и для остальных уравнений:

;

.

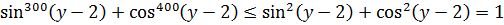
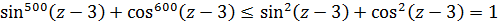
Таким образом, все левые части наших уравнений не больше единички.

Разбираемся теперь с правыми частями. Во-первых, квадратный трёхчлен. Тот, что с параметром. Он в каждом уравнении один и тот же. Выделим полный квадрат и оценим:

А теперь анализируем всю конструкцию справа (например, у первого уравнения)

Радикалы — в любом случае неотрицательные величины. А это значит, что вся правая часть — не меньше единички:

Причём равенство достигается только при a = 2 и y = 2, z = 3.

Ну вот. А теперь берём каждое уравнение и состыковываем все наши оценки:

И последняя задачка, которую мы рассмотрим в данном уроке, — это уже типичная задачка из ЕГЭ. Поэтому собираем волю в кулак, устраиваемся поудобнее, запасаемся попкорном терпением и читаем/смотрим. 🙂

Пример 9

Найдите все значения параметра a , при каждом из которых уравнение

имеет хотя бы один корень.

Задачка эта требует достаточно кропотливого решения. Тем не менее его вполне можно провести, если чётко видеть цель. Я не просто подробно оформлю решение этой задачи, но и объясню, как именно надо «видеть цель». 🙂 Итак, начнём.)

Во-первых, неплохо было бы растащить по разным частям логарифм и линейные конструкции с модулями. Пока они у нас намешаны в одну кучу. Действуем:

Так, что дальше? Дальше можно упростить аргумент логарифма: там явно напрашивается выделение полного квадрата. Упрощаем:

.

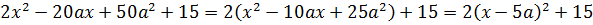
Прекрасно! Значит, всё наше злое уравнение перепишется вот в таком виде:

Всё. Дальнейшим упрощениям это уравнение уже не поддаётся. Теперь будем анализировать каждую функцию — слева и справа.

Функции разнородны. Причём обе непрерывны на всей числовой прямой. Разнородность подаёт нам знак, что нужно пробовать применять метод оценок. Начнём с логарифма — он проще. 🙂

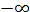
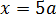
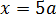
Что можно сказать про аргумент логарифма? Квадратичная функция 2(x-5a) 2 +15, которая сидит внутри логарифма, как и любая парабола ветвями вверх, убывает от до точки (вершины), а потом возрастает. Поэтому в этой точке аргумент логарифма достигает своего наименьшего значения. Стало быть, и сам логарифм по основанию 15 от этой функции в точке также будет достигать своего наименьшего значения, так как функция y = log₁₅x монотонно возрастает. Итак, вся наша функция f(x) ограничена снизу числом f(5a):

Итого, наш логарифм ограничен снизу числом 25.

А вот со второй функцией

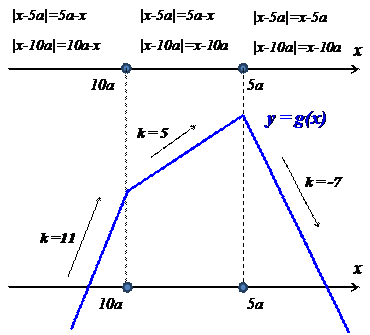
ситуация будет поинтереснее. 🙂 Давайте для начала мысленно представим, как будет выглядеть график этой функции. Переменная икс везде стоит в первой степени, только внутри модулей. Стало быть, в результате раскрытия каждого модуля будет получаться какая-то линейная функция y = kx+b. На каждом промежутке — своя. И поэтому график функции g(x) будет представлять собой ломаную линию, состоящую из кусочков прямых.

Случай 1 (a ≥ 0)

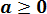
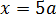
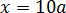
Начнём со случая . В этом случае точка на числовой прямой находится левее точки . И теперь раскрытие модулей по промежуткам не составляет никаких затруднений.

1.1) 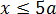. Оба модуля раскрываются с минусом:

Значит, на этом интервале наша функция g(x) – часть возрастающей прямой с угловым коэффициентом 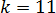. Переходим к следующему промежутку.

1.2) 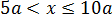. Модули раскрываются с разными знаками:

На этом интервале получили убывающую прямую с угловым коэффициентом 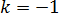. Идём дальше.

1.3) 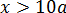. Оба модуля раскрываются с плюсом:

Здесь наша функция ещё сильнее убывает. 🙂 Угловой коэффициент .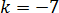

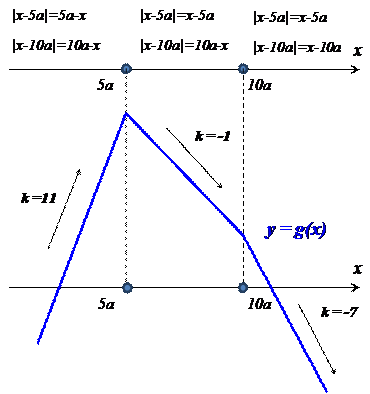
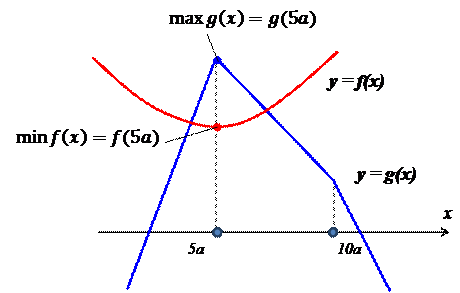
Итак, все три подслучая рассмотрены. A теперь — собираем воедино результаты наших исследований и рисуем схематичный график. 🙂

Зачем мы нарисовали этот график? А затем, что из графика теперь хорошо видно, что наша функция g(x) в точке 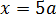достигает своего наибольшего значения. То есть, ограничена сверху числом g(5a).

Сосчитаем это число:

Теперь вспоминаем — чего от нас хотят-то? А то так и про основной вопрос задачи невольно забываешь.) Нас просят решить уравнение f(x) = g(x).

При этом про функции f и g мы знаем, что в одной и той же точке 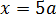они достигают своих экстремальных значений: f – наименьшего, а g – наибольшего. Стало быть, чтобы уравнение f(x) = g(x) имело хотя бы один корень, необходимо и достаточно, чтобы

Да! В данной ситуации это требование является как необходимым, так и достаточным, потому что экстремальные значения принимаются функциями в одной точке, а не в разных. Смотрим на картинку, почему это так:

Остаётся решить неравенство:

А теперь главное — вспомнить, что здесь мы рассматриваем только .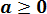

А значит, нам нужно одновременное выполнение этих двух требований:

Итого, первый кусок окончательного ответа — это отрезок

Случай 2 (a ≤ 0)

Рассматриваем теперь отрицательные значения параметра: a

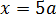
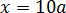
В этом случае будет всё наоборот — точка будет правее точки . Раскрываем модули, никуда не денешься (а я предупреждал, что решение достаточно трудоёмкое, хоть и не такое сложное :)).

2.1)

Функция g(x) – часть возрастающей прямой с угловым коэффициентом .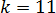

2.2)

Функция g(x) – часть возрастающей прямой с угловым коэффициентом .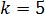

2.3)

Функция g(x) – часть убывающей прямой с угловым коэффициентом .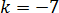

Снова рисуем картинку:

И снова замечаем, что наша функция g(x) достигает своего наибольшего значения в той же самой точке 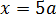. То есть, снова ограничена сверху числом g(5a). Считаем это число:

Думаю, уже особо комментировать не нужно, что нам снова надо решить неравенство:

Получили одно единственное решение неравенства — минус пять. Бывает.) Естественно, требованию 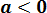минус пятёрка вполне себе удовлетворяет. 🙂 Значит, ещё одним куском ответа является изолированная точка <-5>.

Фуух! Ну что, поздравляю всех, кто дочитал и особенно — тех, кто разобрался! Осталось лишь обе части ответа сложить в кучу.

Всё, задача полностью решена. 🙂

Заключение:

Если слева и справа стоят функции разной природы, то пробуем оценивать левую и правую части. Помогает в 99% случаев.

Не боимся «страшного» вида задачи. 🙂 В большинстве случаев, как ни парадоксально, чем страшнее и безнадёжнее выглядит задача, тем проще её свести к нескольким простейшим, которые уже решаются по стандартной технологии. Как? Оцениваем сначала внешний вид конструкции, выявляем её тип — сумма взаимно обратных величин, квадратный трёхчлен, синусы, модули и т.п. А потом — оцениваем саму конструкцию. Уже теми приёмами и методами, что приведены в этом материале. 🙂

Также не боимся ситуации, когда число уравнений меньше числа неизвестных. Как правило, недостающее звено легко получить, используя те же самые разобранные нами оценки.

Тренируемся и набиваем руку! Без серьёзного опыта здесь — никак. В продаже появилось несметное количество сборников задач ЕГЭ, методичек именно по задачам с параметрами с огромным количеством задач для тренировки. На моём сайте тоже обязательно будут разбираться различные задачи с параметрами из ЕГЭ и даже с мехмата. И обязательно будут задачи для самостоятельного решения. 🙂 В особом разделе, который на пятёрку. 🙂

А у меня на сегодня всё. Всем спасибо за внимание и до новых встреч! 🙂

Источник