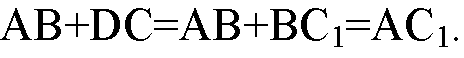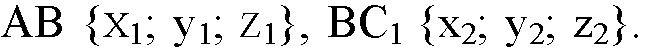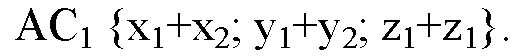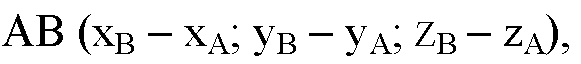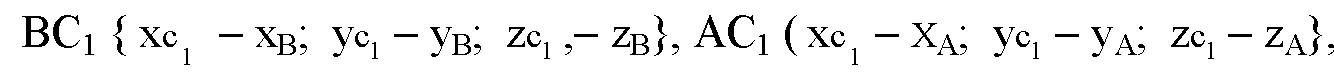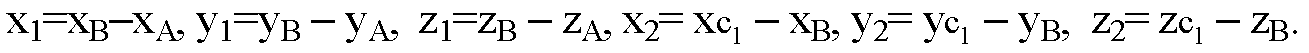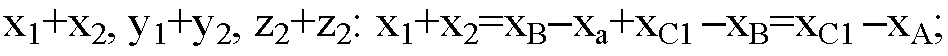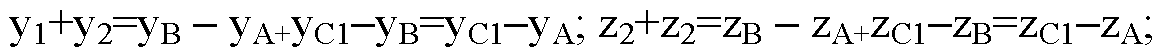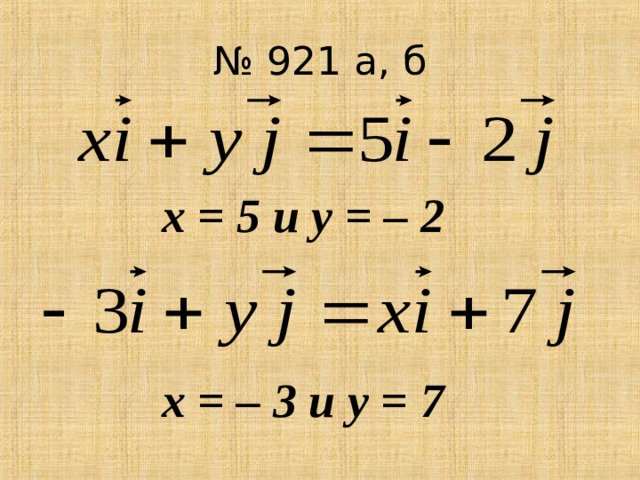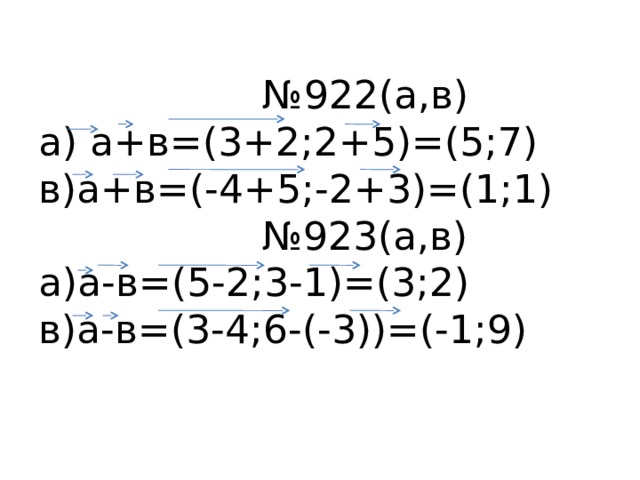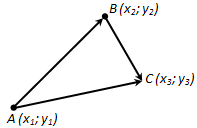Докажите что каждая координата суммы разности двух векторов равна сумме

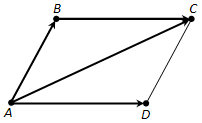
406. Докажите, что каждая координата суммы (разности) двух векторов равна сумме (разности) соответствующих координат этих векторов

Глава V. Метод координат в пространстве. § 1. Координаты точки и координаты вектора. → номер 406

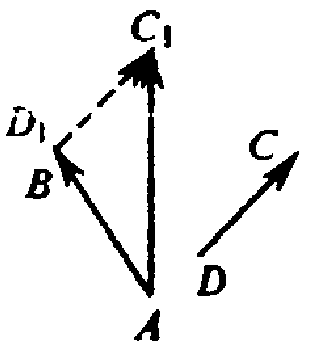
Рассмотрим общий случай. Рассмотрим два некомпланарных вектора AB и DC. Перенесем вектор DC параллельно так, чтобы точка D1 его начала совпала с точкой В конца первого вектора. Получим вектор D1C1 или, что то же самое, вектор ВС1 сонаправленный с вектором DC и равный ему по длине. Согласно правилу сложения векторов:

Для доказательства выразим координаты этих векторов через координаты

Из обозначения координат вектора AB как х1, у1 и z1 и вектора BC1 как x2, у2, z2, получим

Суммы координат x1+x2, y1+y2, z1+z2 являются координатами вектора АС1 равного сумме исходных двух векторов AB и DC. Что и требовалось доказать.

Источник

Помогите Пожалуйста с вопросами по геометрии (9 класс)!

1)Сформулируйте и докажите лемму о коллинеарных векторах.
2)Что значит разложить вектор по двум данным векторам.
3)Сформулируйте и докажите теорему о разложении вектора по двум неколлинеарным векторам.
4)Объясните, как вводится прямоугольная системы координат.
5)Что такое координатные векторы?
6)Сформулируйте и докажите утверждение о разложении произвольного вектора по координатным векторам.
7)Что такое координаты вектора?
8)Сформулируйте и докажите правила нахождения координат суммы и разности векторов, а также произведения вектора на число по заданным координатам векторов.
9)Что такое радиус-вектора точки? Докажите, что координаты точки равны соответствующим координатам векторов.
10)Выведите формулы для вычисления координат вектора по координатам его начала и конца.
11)Выведите формулы для вычисления координат вектора по координатам его концов.
12) Выведите формулу для вычисления длины вектора по его координатам.
13)Выведите формулу для вычисления расстояния между двумя точками по их координатам.
14)Приведите пример решения геометрической задачи с применением метода координат.
15)Какое уравнение называется уравнением данной линии? Приведите пример.
16)Выведите уравнение окружности данного радиуса с центром в данной точке.
17)Напишите уравнение окружности данного радиуса с центром в начале координат.
18)Выведите уравнение данной прямой в прямоугольной системе координат.
19)Напишите уравнение прямых, проходящих через данную точку M0 (X0 : Y0) и параллельных осям координат.
20)Напишите уравнение осей координат.
21)Приведите примеры использования уравнений окружности и прямой при решении геометрических задач.

Пожалуйста очень надо!

В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.

Источник

Координаты вектора

Нахождение координат вектора.

Просмотр содержимого документа
«Координаты вектора»

и – координатные векторы

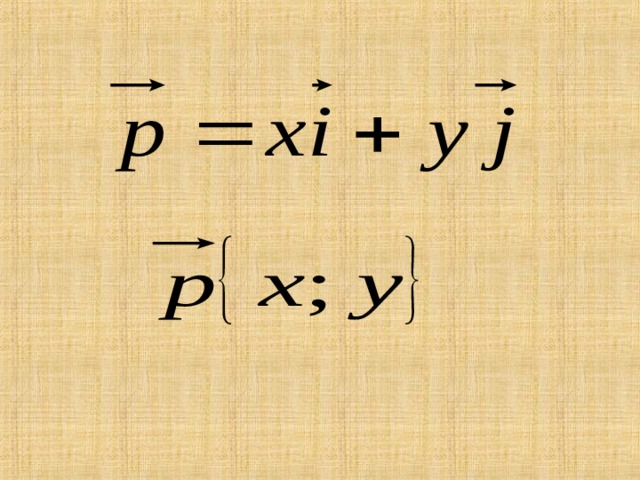
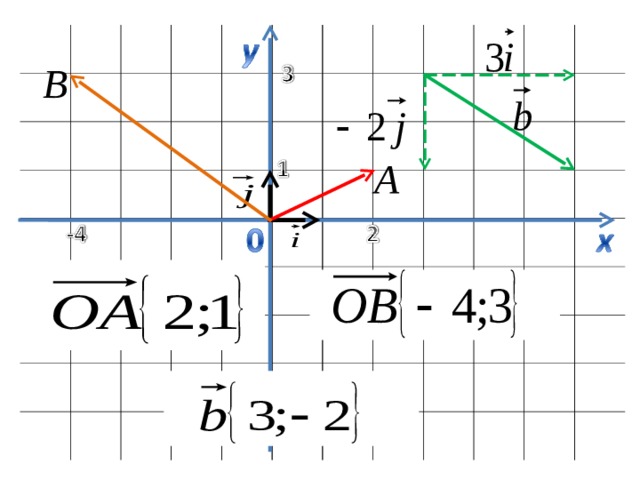
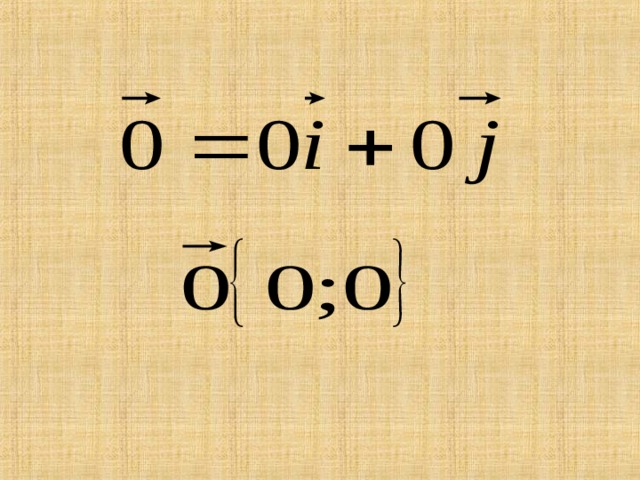
Координаты равных векторов соответственно равны

Доказать: Координаты вектора

Отсюда следует, что координаты суммы двух векторов равны сумме соответствующих координат этих векторов.

Найдём координаты вектора

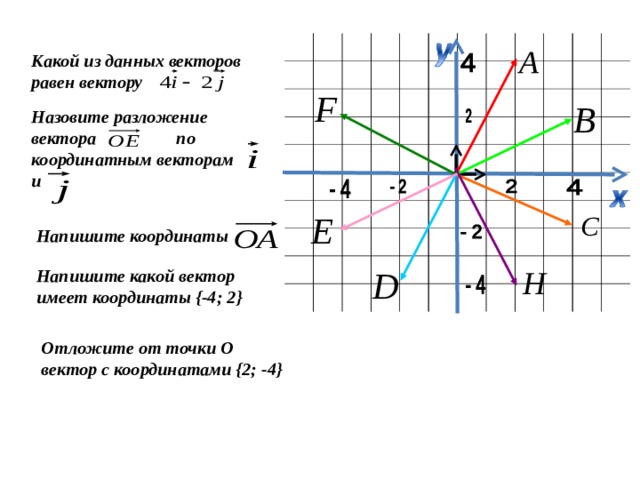
Какой из данных векторов равен вектору

Назовите разложение вектора по координатным векторам и

Найти координаты векторов:

Домашнее задание: п. 87, вопросы 7 – 8. № 918, 919,922(б,г).

Источник

Докажите что каждая координата суммы разности двух векторов равна сумме

Для доказательства достаточно сравнить соответствующие координаты векторов, стоящих в правой и левой частях равенств. Мы видим, что они равны. А векторы с соответственно равными координатами равны.

Для доказательства достаточно сравнить соответствующие координаты векторов, стоящих в правой и левой частях равенств. Мы видим, что они равны. А векторы с соответственно равными координатами равны.

Вопрос 13. Докажите векторное равенство \(\overline + \overline = \overline\).
Ответ. Теорема 10.1. Каковы бы ни были точки A, B, C, имеет место векторное равенство

\(\overline + \overline = \overline\).

Вопрос 15. Сформулируйте «правило параллелограмма» сложения векторов.
Ответ. Для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах («правило параллелограмма», рис. 217). Действительно, \(\overline + \overline = \overline\), а \(\overline = \overline\). Значит, \(\overline + \overline = \overline\).

Вопрос 17. Дайте определение умножения вектора на число.
Ответ. Произведением вектора (a₁; a₂) на число \(\lambda\) называется вектор \(\overline<\lambda\)a₁; \(\lambda\)a₂>), т.е. \((\overline1; a₂>) \lambda = (\overline<\lambda a₁; \lambda a₂>)\).
По определению \((\overline1; a₂>) \lambda = \lambda (a₁; a₂)\).
Из определения операции умножения вектора на число следует, что для любого вектора \(\overline\) и чисел \(\lambda\), \(\mu\)

Источник

Докажите что каждая координата суммы разности двух векторов равна сумме

Сформулируем ряд базовых определений.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.

то есть модуль вектора равен корню квадратному из суммы квадратов его координат.

Обозначим углы между вектором и осями координат через α, β, γ соответственно. Косинусы этих углов называются для вектора направляющими, и для них выполняется соотношение: Верность данного равенства можно показать с помощью свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем пункте 4.

Пусть в трехмерном пространстве заданы векторы своими координатами. Имеют место следующие операции над ними: линейные (сложение, вычитание, умножение на число и проектирование вектора на ось или другой вектор); не линейные – различные произведения векторов (скалярное, векторное, смешанное).

1. Сложение двух векторов производится покоординатно, то есть если

Геометрически два вектора складываются по двум правилам:

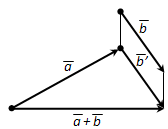
а) правило треугольника – результирующий вектор суммы двух векторов соединяет начало первого из них с концом второго при условии, что начало второго совпадает с концом первого вектора; для суммы векторов – результирующий вектор суммы соединяет начало первого из них с концом последнего вектора-слагаемого при условии, что начало последующего слагаемого совпадает с концом предыдущего;

б) правило параллелограмма (для двух векторов) – параллелограмм строится на векторах-слагаемых как на сторонах, приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой векторов.

Геометрически два вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов является диагональ, соединяющая концы векторов, причем результирующий вектор направлен из конца вычитаемого в конец уменьшаемого вектора.

При λ>0 – вектор сонаправлен ; λ противоположно направлен ; | λ|> 1 – длина вектора увеличивается в λ раз; | λ| 1 – длина вектора уменьшается в λ раз.

4. Пусть в пространстве задана направленная прямая (ось l ), вектор задан координатами конца и начала. Обозначим проекции точек A и B на ось l соответственно через A ’ и B ’.

Рассмотрим некоторые основные свойства проекций:

1) проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью, то есть ;

2.) проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой;

3) проекция суммы нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.

Сформулируем определения и теоремы о произведениях векторов, представляющих нелинейные операции над векторами.

5. Скалярным произведением векторов и называется число (скаляр), равное произведению длин этих векторов на косинус угла φ между ними, то есть

Теорема 2.2. Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения

Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть

Отсюда следует условие перпендикулярности ненулевых векторов и :

С помощью скалярного произведения векторов находят работу постоянной силы на прямолинейном участке пути.

Решение. Вычислим модули векторов и их скалярное произведение по теореме (2.3):

Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых на производство одной тонны творога, заданы в таблице 2.2 (руб.).

Какова общая цена этих ресурсов, затрачиваемых на изготовление одной тонны творога?

Примечание. Действия с векторами, осуществленные в примере 2.10, можно выполнить на персональном компьютере. Для нахождения скалярного произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве аргументов указываются адреса диапазонов элементов матриц, сумму произведений которых необходимо найти. В MathCAD скалярное произведение двух векторов выполняется при помощи соответствующего оператора панели инструментов Matrix

Решение. Находим вектор перемещения, вычитая из координат его конца координаты начала

Угол φ между и находим по формуле (2.29), то есть

– перпендикулярен векторам и ;

– векторы образуют правую тройку (рис. 2.15).

Примечание. Определитель (2.25) раскладывается по свойству 7 определителей

Следствие 1. Необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их соответствующих координат

Следствие 2. Векторные произведения единичных орт равны

Следствие 3. Векторный квадрат любого вектора равен нулю

Также с помощью векторного произведения можно определить момент силы относительно точки и линейную скорость вращения.

— перпендикулярен плоскости, проходящей через точки O , A , B ;

Следовательно, момент силы относительно точки O представляет собой векторное произведение

Решение. Найдем векторное произведение заданных векторов по формуле (2.32).

Теорема 2.6. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения

Теорема 2.7. Если три вектора заданы своими координатами, то их смешанное произведение представляет собой определитель третьего порядка, составленный из координат векторов- сомножителей соответственно, то есть

Объем треугольной пирамиды, построенной на этих же векторах, равен

Решение. Найдем координаты векторов

По формуле (2.36) объем пирамиды, построенной на векторах равен (единиц объема)

Рассмотрим очень важный вопрос о разложении вектора по базису. Приведем следующие определения.

получим выражение вектора через остальные векторы

Линейно независимыми называют векторы, если равенство (2.37) выполняется только тогда, когда все

Базисом n – мерного пространства E_n называют любую совокупность линейно независимых векторов n – мерного пространства.

Произвольный вектор n – мерного пространства можно представить в виде линейной комбинации векторов базиса таким образом:

Линейное пространство называется конечномерным и имеет размерность n , если в этом пространстве существует система из n линейно независимых векторов (базис) такая, что каждое ее расширение приводит к линейной зависимости системы.

Источник