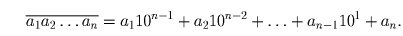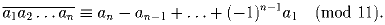Докажите что количество трехзначных чисел

Докажи, что если к любому трехзначному числу приписать трехзначное число, записанное теми же цифрами, но в обратном порядке, то получится число, делящееся на 11?

Докажи, что если к любому трехзначному числу приписать трехзначное число, записанное теми же цифрами, но в обратном порядке, то получится число, делящееся на 11.

Допустим возьмём число 356 если приписать это число наоборот то получится 356653 и если его разделить на одиннадцать, то выйдет 33233.

СКОЛЬКО ТРЕХЗНАЧНЫХ ЧИСЕЛ ОБЛАДАЕТ СЛЕДУЮЩИМ СВОЙСТВОМ : ЕСЛИ ИЗ ТАКОГОЧИСЛА ВЫЧЕСТЬ 297, ТО ПОЛУЧИТСЯ ТРЕХЗНАЧНОЕ ЧИСЛО, ЗАПИСАННОЕ ТЕМИ ЖЕ ЦИФРАМИ, НО В ОБРАТНОМ ПОРЯДКЕ?

СКОЛЬКО ТРЕХЗНАЧНЫХ ЧИСЕЛ ОБЛАДАЕТ СЛЕДУЮЩИМ СВОЙСТВОМ : ЕСЛИ ИЗ ТАКОГОЧИСЛА ВЫЧЕСТЬ 297, ТО ПОЛУЧИТСЯ ТРЕХЗНАЧНОЕ ЧИСЛО, ЗАПИСАННОЕ ТЕМИ ЖЕ ЦИФРАМИ, НО В ОБРАТНОМ ПОРЯДКЕ.

Докажите, что разность любого трехзначного числа и трехзначного числа, записанного теми же цифрами, но в обратном порядке, делится на 9?

Докажите, что разность любого трехзначного числа и трехзначного числа, записанного теми же цифрами, но в обратном порядке, делится на 9.

Докажите, что разность между трехзначным числом и числом, записанным этими же цифрами, но в обратном порядке, делится на 99?

Докажите, что разность между трехзначным числом и числом, записанным этими же цифрами, но в обратном порядке, делится на 99.

Трехзначное число больше числа, записанного теми же цифрами, но в обратном порядке, на 495?

Трехзначное число больше числа, записанного теми же цифрами, но в обратном порядке, на 495.

Сумма цифр этого трехзначного числа равна 17, а сумма квадратов его цифр равна 109.

Найти такое трехзначное число.

Сумма цифр трехзначного числа равна 17?

Сумма цифр трехзначного числа равна 17.

Если из исходного числа вычесть число, записанное теми же цифрами, но в обратном порядке, то получится 792.

Найти трехзначное число.

Докажите что разность любого трехзначного числа и числа записанного теми же цифрами но в обратном порядке делится на 9?

Докажите что разность любого трехзначного числа и числа записанного теми же цифрами но в обратном порядке делится на 9.

Трехзначное число больше числа, записанного теми же цифрами, но в обратном порядке, на 495?

Трехзначное число больше числа, записанного теми же цифрами, но в обратном порядке, на 495.

Сумма цифр этого трехзначного числа равна 17, а сумма квадратов его цифр равна 109.

Найти такое трехзначное число.

Сколько трехзначных чисел обладает следующим свойством : если из такого числа вычесть 297, то получиться трехзначное число, записанное теми же цифрами, но в обратном порядке?

Сколько трехзначных чисел обладает следующим свойством : если из такого числа вычесть 297, то получиться трехзначное число, записанное теми же цифрами, но в обратном порядке?

Сумма цифр трехзначного числа равна 17?

Сумма цифр трехзначного числа равна 17.

Если из исходного числа вычесть число, записанное теми же цифрами, но в обратном порядке, то получится 792.

Найти трехзначное число.

Докажите что если к любому трёхзначному числу приписать трёхзначное число записанное теми же цифрами но в обратном порядке то получится число делящиеся на число 11?

Докажите что если к любому трёхзначному числу приписать трёхзначное число записанное теми же цифрами но в обратном порядке то получится число делящиеся на число 11.

Источник

Докажите что количество трехзначных чисел

Задача 24:

Докажите, что любое натуральное число сравнимо со своей последней цифрой по модулю а) 10; б) 2; в) 5.

Решение:

Вычтем из числа его последнюю цифру и получим число, оканчивающееся нулем, т.е. делящееся на 10 (а значит, и на 5, и на 2).

Задача 25:

Докажите, что .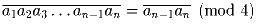

Решение:

Указание: все степени десяти, начиная со 100, делятся на 4.

Задача 26:

Решение:

Число делится на 2 n (на 5 n ) тогда и только тогда, когда число, образованное его последними n цифрами, делится на 2 n (на 5 n ).

Задача 27:

Последняя цифра квадрата натурального числа равна 6. Докажите, что его предпоследняя цифра нечетна.

Решение:

Так как последняя цифра 6, то возводимое в квадрат число четно. Раз оно является квадратом, то оно делится и на 4. Следовательно, число, составленное из двух его последних цифр, должно делиться на 4. Все требуемые двузначные числа легко выписать: 16, 36, 56, 76, 96.

Задача 28:

Предпоследняя цифра квадрата натурального числа – нечетная. Докажите, что его последняя цифра 6.

Решение:

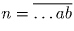
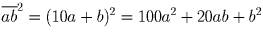
Две последние цифры квадрата числа n зависят только от двух последних цифр числа n. Пусть . Тогда . Ясно, что цифра десятков числа b² должна быть нечетной. Прямой перебор показывает, что цифра единиц должна тогда быть равной 6.

Задача 29:

Докажите, что степень двойки не может оканчиваться четырьмя одинаковыми цифрами.

Решение:

Рассмотрите остатки по модулю 16.

Задача 30:

Найдите 100-значное число без нулевых цифр, которое делится на сумму своих цифр.

Решение:

Подберем число так, чтобы сумма его цифр равнялась 125. Делимость числа на 125 определяется тремя его последними цифрами. Следовательно, годится число 111 … 11599125 (в начале записи единица написана 94 раза).

Задача 31:

Докажите, что любое натуральное число сравнимо с суммой своих цифр по модулю а) 3; б) 9.

Решение:

Ясно, что 10 ≡ 1 (mod %)%9. Поэтому 10 k ≡ 1 (mod 9) для любого натурального k. Таким образом, a ₁ 10 n – 1 + a ₂ 10 n – 2 + … + a _{n – 1} 10¹ + a _n ≡ a ₁ + a ₂ + … + a _n (mod %)%9. Рассуждения для числа 3 совершенно аналогичны.

Задача 32:

Решение:

а) нет; б) нет. Рассмотрите остатки по модулю 9.

Задача 33:

У числа 2¹ºº нашли сумму цифр, у результата снова нашли сумму цифр и т.д. В конце концов получилось однозначное число. Найдите его.

Решение:

Задача 34:

Докажите, что если записать в обратном порядке цифры любого натурального числа, то разность исходного и нового числа будет делиться на 9.

Решение:

Эти числа имеют одинаковые суммы цифр и, значит, одинаковые остатки по модулю 9.

Задача 35:

К числу 15 припишите слева и справа по одной цифре так, чтобы полученное число делилось на 15.

Решение:

Это можно сделать шестью способами: 1155, 4155, 7155, 3150, 6150, 9150.

Задача 36:

Сколько имеется четырехзначных чисел, которые делятся на 45, а две средние цифры у них – 97?

Решение:

Два числа: 6975, 2970.

Задача 37:

Найдите наименьшее натуральное число, делящееся на 36, в записи которого встречаются все 10 цифр.

Решение:

Это число 1023457896.

Задача 38:

Докажите, что произведение последней цифры числа 2 n и суммы всех цифр этого числа, кроме последней, делится на 3.

Решение:

Разберите два случая: последняя цифра равна или не равна 6.

Задача 39:

Может ли сумма цифр точного квадрата равняться 1970?

Решение:

Нет. Рассмотрите остатки по модулю 3.

Задача 40:

Из трехзначного числа вычли сумму его цифр. С полученным числом проделали то же самое и так далее, 100 раз. Докажите, что в результате получится нуль.

Решение:

Задача 41:

Решение:

Задача 42:

Решение:

Указание: 10 ≡ – 1 (mod 11).

Задача 43:

Докажите, что число 111 … 11 (2n единиц) – составное.

Решение:

Это число делится на 11.

Задача 44:

Докажите, что число 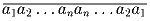– составное.

Решение:

Это число делится на 11.

Задача 45:

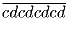
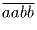
Пусть a, b, c, d – различные цифры. Докажите, что не делится на .

Решение:

делится на 11, а – нет.

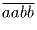
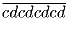
Задача 46:

A – шестизначное число, в записи которого по одному разу встречаются цифры 1, 2, 3, 4, 5, 6. Докажите, что A не делится на 11.

Решение:

Цифры 1, 2, 3, 4, 5, 6 нельзя разбить на две тройки, разность сумм в которых делится на 11.

Задача 47:

Докажите, что разность числа, имеющего нечетное количество цифр, и числа, записанного теми же цифрами, но в обратном порядке, делится на 99.

Решение:

Эти два числа имеют одинаковые остатки как при делении на 9, так и при делении на 11.

Задача 48:

Можно ли составить из цифр 2, 3, 4, 9 (каждую цифру можно использовать сколько угодно раз) два числа, одно из которых в 19 раз больше другого?

Решение:

Нельзя. Проследите за последней цифрой.

Задача 49:

Сумма двух цифр a и b делится на 7. Докажите, что число 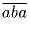также делится на 7.

Решение:

.

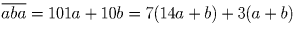
Задача 50:

Сумма цифр трехзначного числа равна 7. Докажите, что это число делится на 7 тогда и только тогда, когда две его последние цифры равны.

Решение:

, так как 2(a + b + c) ≡ 0 (mod 7). Значит, делится на 7 тогда и только тогда, когда b – c делится на 7. Но так как b, c

Источник

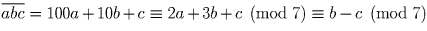
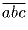
Муниципальный этап 2021 олимпиада по математике задания и ответы для 6-11 класса ВСОШ

ПОДЕЛИТЬСЯ

Олимпиада по математике муниципальный этап 2021-2022 официальные задания, решения и ответы для 6,7, 8, 9, 10, 11 класса. Официальная всероссийская олимпиада школьников ВСОШ прошла в Московской области 13 ноября 2021 года.

Скачать задания и ответы

Муниципальный этап 2021 олимпиады по математике 6-11 класс задания и ответы:

1)Найдите самое маленькое число, у которого все цифры различны, сумма первых двух цифр (слева) делится на 2, сумма первых трёх цифр делится на 3, сумма первых четырёх цифр делится на 4, первых пяти цифр делится на 5, первых шести цифр делится на 6.

2)В Солнечном городе 5 коротышек едят пончики ежедневно, 7 коротышек едят пончики через день, а остальные вообще не едят пончики. Вчера 9 коротышек ели пончики. Сколько коротышек будут есть пончики сегодня?

3)Бегун пробежал в первом забеге два круга по стадиону со скоростью v за 4 минуты. Во второй раз он пробежал первый круг со скоростью p, а второй круг со скоростью v/2 и потратил на второй забег 5 минут. Найдите отношение v : p.

4)На болоте по кругу расположены 6 кочек, соединенных дорожками так, как показано на рисунке. На каждой дорожке сидело несколько лягушек (не обязательно равное количество). Затем каждая лягушка поймала на своей дорожке по 10 мух, и положила по 5 мух на каждую из двух кочек, которые соединяла ее дорожка. На пяти кочках указано, сколько мух на них оказалось в итоге. Сколько мух могло оказаться на шестой кочке?

5)Заметим, что каждая лягушка положила по 5 мух на одну белую и на одну серую кочку. Это значит, что суммарное количество мух, оказавшихся на серых кочках равно количеству мух, оказавшихся на белых кочках (а также в 5 раз больше общего количества лягушек). 1) 85 + 40 + 55 = 180 (мух) – всего; 2) 180 − 50 − 65 = 65 – на шестой кочке.

6)За круглый стол сели 9 человек – лжецы и рыцари. Лжецы всегда лгут, а рыцари всегда говорят правду. Каждому из них дали по монете. Затем каждый из сидящих передал свою монету одному из двух своих соседей. После чего каждый сказал: «У меня монет больше, чем у соседа справа». Какое наибольшее число рыцарей могло сидеть за столом?

8)В Солнечном городе 6 коротышек едят пончики ежедневно, 8 коротышек едят пончики через день, а остальные вообще не едят пончики. Вчера 11 коротышек ели пончики. Сколько коротышек будут есть пончики сегодня?

9)У Васи и Миши телефоны показывают 15% заряда. А через час у Васи – 11%, у Миши – 12%. Может ли телефон Миши разрядиться раньше телефона Васи, если телефоны разряжаются равномерно, а показываемый процент заряда – это округленное до целых значение заряда?

10)Даны девять карточек, на которых написаны числа 5, 5, 6, 6, 6, 7, 8, 8, 9. Из этих карточек сложили три трёхзначных числа A, B, C, у каждого из которых все три цифры разные. Какое наименьшее значение может быть у выражения A + B − C?

11)За круглый стол сели 10 человек – лжецы и рыцари. Лжецы всегда лгут, а рыцари всегда говорят правду. Каждому из них дали по монете. Затем каждый из сидящих передал свою монету одному из двух своих соседей. После чего 5 человек сказали: «У меня одна монета», а остальные 5 сказали: «У меня нет монет». Какое наибольшее число рыцарей могло сидеть за столом?

13)Найдите наибольшее натуральное число, все цифры которого различны, при этом такое, что сумма любых двух его цифр — простое число.

14)У Васи и Миши телефоны показывают 15% заряда. А через час у Васи – 11%, у Миши – 12%. Может ли телефон Миши разрядиться раньше телефона Васи, если телефоны разряжаются равномерно, а показываемый процент заряда – это целая часть значения заряда? Целая часть числа A – это наибольшее целое число, не превосходящее A.

15)Дан прямоугольный треугольник ABC (AB – гипотенуза). На большем катете AC треугольника ABC выбрана точка K так, что AK = BK. Пусть CH – высота треугольника ABC, и точка M симметрична точке B относительно точки H. Докажите, что отрезки BK и CM перпендикулярны.

16)За круглый стол сели 10 человек – лжецы и рыцари. Лжецы всегда лгут, а рыцари всегда говорят правду. Каждому из них дали по монете. Затем каждый из сидящих передал свою монету одному из двух своих соседей. После чего каждый сказал: «У меня монет больше, чем у соседа справа». Какое наибольшее число рыцарей могло сидеть за столом?

17)Если из дискриминанта трехчлена f(x) = ax2 + 2bx + c вычесть дискриминант трехчлена g(x) = (a + 1)x 2 + 2(b + 2)x + c + 4, то получится 24. Найдите f(−2).

18)За круглый стол сели 6 человек – лжецы и рыцари. Лжецы всегда лгут, а рыцари всегда говорят правду. Каждому из них дали по монете. Затем каждый из сидящих передал свою монету одному из двух своих соседей. После чего 3 человек сказали: «У меня одна монета», а остальные 3 сказали: «У меня нет монет». Какое наибольшее число рыцарей могло сидеть за столом?

19)На доске написано N простых чисел (не обязательно различных). Оказалось, что сумма любых трех чисел на доске — тоже простое число. При каком наибольшем N это возможно?

20)Вася вырезал из картона треугольник и занумеровал его вершины цифрами 1, 2 и 3. Оказалось, что если Васин треугольник повернуть по часовой стрелке вокруг его вершины под номером 1 на угол равный углу при этой вершине 15 раз, то треугольник вернется в исходное положение. Если повернуть по часовой стрелке Васин треугольник вокруг его вершины под номером 2 на угол равный углу при этой вершине 6 раз, то треугольник вернется в исходное положение. Вася утверждает, что если повернуть его треугольник вокруг вершины под номером 3 на угол равный углу при этой вершине n раз, то треугольник вернется в исходное положение. Какое минимальное n мог назвать Вася так, чтобы его утверждение было правдивым хотя бы при каком-то картонном треугольнике?

21)В прямоугольном неравнобедренном треугольнике ABC с прямым углом C проведена биссектриса CL. Точка K выбрана на гипотенузе этого треугольника так, что AL = BK. Перпендикуляр к AB, проходящий через точку K, пересекает луч CL в точке N. Докажите, что KN = AB.

24)Даны три квадратных трехчлена f(x) = ax2+bx+c, g(x) = bx2+cx+a, h(x) = cx2+ ax+b, где a, b, c – различные ненулевые действительные числа. Из них составили три уравнения f(x) = g(x), f(x) = h(x), g(x) = h(x). Найдите произведение всех корней этих трех уравнений, если известно, что каждое из них имеет по два различных корня

25)На продолжении стороны AC треугольника ABC за точку C выбрана точка D. Пусть S1 – окружность, описанная около треугольника ABD, S2 – окружность, описанная около треугольника CBD. Касательная к окружности S1, проходящая через точку A, и касательная к окружности S2, проходящая через точку C, пересекаются в точке P. Докажите, что точка P лежит на окружности, описанной около треугольника ABC.

26)Дан «скелет» клетчатого квадрата 10 × 10 (то есть множество из вертикальных и горизонтальных отрезков, делящих квадрат на квадратики со стороной 1, включая границу квадрата). И этот скелет разбили на уголки (из двух единичных отрезков) и отрезки длины 2 (тоже из двух единичных отрезков). Могло ли «отрезков длины 2» быть ровно 21?

27)Из трёхзначного числа A, не содержащего в записи нулей, получили двухзначное число B, записав вместо первых двух цифр их сумму (например, число 243 превращается в 63). Найдите A если известно, что A = 3B.

Источник