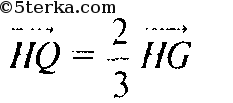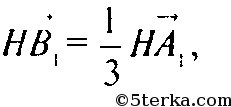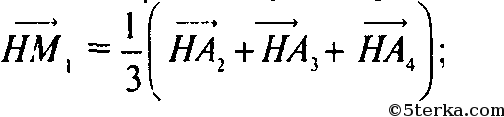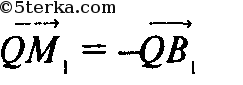Докажите что медианы тетраэдра пересекаются в одной точке
Докажите что медианы тетраэдра пересекаются в одной точке
ТЕТРАЭДР. ВИДЫ ТЕТРАЭДРОВ
Тетраэдр является одним из простейших многогранников, гранями которого являются четыре треугольника. Его можно считать пространственным аналогом треугольника. Рассмотрим свойства треугольников и аналогичные им свойства тетраэдров.
Теорема 1. Биссектрисы треугольника пересекаются в одной точке – центре вписанной окружности.
Теорема 1′. Биссектральные плоскости двугранных углов тетраэдра пересекаются в одной точке – центре вписанной сферы.
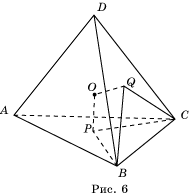
Доказательство. Пусть ABCD – тетраэдр. Пересечением биссектральных плоскостей двугранных углов с ребрами AB, AC,и BC (рис. 1) является точка O, равноудаленная от всех граней тетраэдра. Следовательно, эта точка принадлежит биссектральным плоскостям остальных двугранных углов тетраэдра и является центром вписанной сферы.
Теорема 9′ (Чевы). Пусть на ребрах AB, BC, CD и AD тетраэдра ABCD взяты соответственно точки A 1 , B 1 , C 1 и D 1. Плоскости ABC 1 , BCD 1 , CDA 1 и DAB 1 пересекаются в одной точке тогда и только тогда, когда
Рассмотрим теперь некоторые специальные тетраэдры.
Равногранным тетраэдром называется тетраэдр, у которого все грани равны.
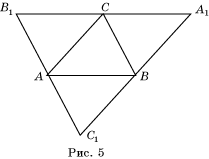
Теорема 10. Для любого остроугольного треугольника существует равногранный тетраэдр, грани которого равны данному треугольнику.
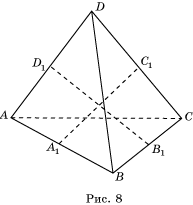
Доказательство. Пусть ABC – произвольный остроугольный треугольник. Через его вершины проведем прямые, параллельные противоположным сторонам (рис. 5).
Покажем обратное, пусть ABCD – равногранный тетраэдр, O – цетр описанной сферы. Тогда плоскости граней пересекают описанную сферу по окружностям одинакового радиуса. Следовательно, расстояния от точки O до граней тетраэдра равны и, значит O – центр вписанной сферы.
Прямоугольным тетраэдром называется тетраэдр, у которого все плоские углы при какой-нибудь вершине прямые.
Теорема 12. Основанием высоты прямоугольного тетраэдра, проведенной из вершины с прямыми плоскими углами, является точка пересечения высот противоположной грани.
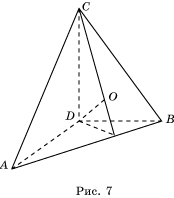
Теорема 13. (Пифагора) Квадрат площади грани прямоугольного тетраэдра, лежащей против вершины с прямыми плоскими углами, равен сумме квадратов площадей остальных граней этого тетраэдра.
Доказательство. Пусть ABCD – прямоугольный тетраэдр (рис. 7). Плоские углы при вершине D прямые. Можно было бы обозначить ребра, выходящие из вершины D через a, b, c, а затем воспользоваться формулой Герона для нахождения площади треугольника ABC .
Тогда A 1 B 1 D 1 C 1 – параллелограмм. Его диагонали равны тогда и только тогда, когда он – прямоугольник, т.е. AC 
BD .
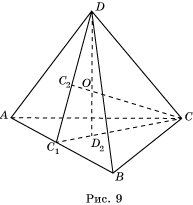
Теорема 2. Тетраэдр является ортогональным тогда и только тогда, когда он является ортоцентрическим.
Доказательство. Пусть ABCD – ортогональный тетраэдр (рис. 9). DD 2 – высота, опущенная из вершины D. Плоскость CDD 2 перпендикулярна AB и, следовательно, DC 1 и CC 1 – высоты треугольников ABC и ABD. Высоты DD 2 и CC 2 треугольника C 1 CD пересекаются.
Литература
1. Адамар Ж. Элементарная геометрия. Часть II. Стереометрия. – М.: Учпедгиз, 1938.
2. Перепелкин Д.И. Курс элементарной геометрии. Часть II. Геометрия в пространстве. – М.-Л.: Гостехиздат, 1949.
3. В.В.Прасолов, И.Ф.Шарыгин. Задачи по стереометрии. – М.: Наука, 1989.
4. Д.О.Шклярский, Н.Н.Ченцов, И.М.Яглом. Избранные задачи и теоремы элементарной математики. Часть 3. – М.: Государственное издательство технико-теоретической литературы, 1954.
Доказать, что медианы тетраэдра пересекаются в одной точке
Доказать, что медианы треугольника пересекаются в одной точке и делятся в отношении 2 : 1.
Доказать, что медианы треугольника пересекаются в одной точке и делятся в отношении 2 : 1.
Докажите, что все четыре медианы пересекаются в одной точке и точкой пересечения делятся в соотношении 3:1
Медианой четырёхугольника назовем отрезок, соединяющий какую-нибудь из его вершин с центром медиан.
Доказать, что плоскости пересекаются в одной точке
Доказать, что плоскости 2х-3у-z+15=0 3x+y-4z=0 и 5x-2y+3z-1=0 пересекаются в одной точке и найти.
Доказать, что прямые на которых лежат высоты тупоугольного треугольника пересекаются в одной точке
как доказать, что прямые на которых лежат высоты тупоугольного треугольника пересекаются в одной.
Медианы АМ и ВР треугольника АВС пересекаются в точке О
Помогите пожалуйста решить задачу! Медианы АМ и ВР треугольника АВС пересекаются в точке О.
Докажите, что отрезки пересекаются в одной точке
Четырехугольник ABCD-параллелограмм; O1 и О2- центры окружностей, вписанных в D ABC и в D ADC.
В правильном n-угольнике провели несколько диагоналей, причем никакие три не пересекаются в одной точке
В правильном n-угольнике провели несколько диагоналей, причем никакие три не пересекаются в одной.
Докажите что медианы тетраэдра пересекаются в одной точке
а) Докажите, что медианы тетраэдра (отрезки, соединяющие вершины с точками пересечения медиан противоположных граней) и отрезки, соединяющие середины противоположных ребер, пересекаются в одной точке.
б) Дан тетраэдр 
с прямыми плоскими углами при вершине 
Площади граней 
и 
равны соответственно 132, 150, 539. Найдите объем тетраэдра.
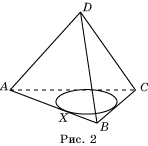
1. Рассмотрим грани ABC и ABD. Пусть M — точка пересечения медиан Δ ABC, N — треугольника ABD. И пусть K — середина AB. Точки C, D, M, N, K лежат в одной плоскости, коли они принадлежат двум пересекающимся прямым KC и KD. Поскольку KC : KM = KD : KN = 3 : 1, треугольники MKN и CKD гомотетичны с коэффициентом гомотетии (подобия) k = 3. По основному свойству гомотетии будем иметь: CD || MN, CD = 3MN.
Соединим отрезками точки: M и D, N и С. Точку пересечения MD с NC обозначим О.
Аналогично можно доказать, что через точку О пройдут все остальные медианы заданного тетраэдра.
2. Теперь докажем, что через точку О пройдут и отрезки, соединяющие середины противоположных ребер тетраэдра (рисунок 2).
Пусть L — середина ребра BC. В плоскости DKC через точку D проведем прямую, параллельную KC. Проведем также прямую KL, которая пересечет только что проведенную прямую в точке, которую обозначим P.
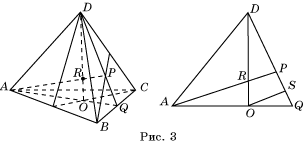
Пусть O1 точка пересечения DM и KL.
Рассмотрим Δ KLC и Δ PLD. У них: ∠KLC = ∠PLD как вертикальные, ∠KCL = ∠ PDL как внутренние накрест лежащие при KC || PD и секущей DC, CL = DL. Тогда Δ KLC = Δ PLD — по второму признаку равенства треугольников. Отсюда: KC = PD, KL = PL, ∠CKL = ∠BPL.
В Δ KO1M и Δ PO1D ∠KO1M = ∠ PO1D как вертикальные, ∠MKO1 = ∠DPO1 по ранее доказанному. Значит, 
откуда DO1 : O1M = PD : KM. Но как доказано выше, KC = PD. Следовательно, O1D : O1M = KC : KM = 3 : 1.
Итак, O1D : O1M = 3 : 1. Выше было доказано, что OD : OM = 3 : 1. Так как отрезок DM можно разделить в отношении 3 : 1, считая от точки D, единственным образом, то точки О и O1 совпадут, то есть KL проходит через точку О. Совершенно аналогично можно доказать то, что отрезки, соединяющие середины ребер BC и AD, BD и AC, пройдут через точку О. И это — все то, что требовалось доказать.
б) Введем обозначения длин ребер тетраэдра: пусть BD = a, CD = c, AD = b.
815. Дан тетраэдр, все высоты которого пересекаются в одной точке. Докажите, что точки пересечения медиан всех граней, основания высот тетраэдра и точки, которые делят каждый из отрезков, соединяющих точку пересечения высот с вершинами, в отношении 2:1, с
815. Дан тетраэдр, все высоты которого пересекаются в одной точке. Докажите, что точки пересечения медиан всех граней, основания высот тетраэдра и точки, которые делят каждый из отрезков, соединяющих точку пересечения высот с вершинами, в отношении 2:1, считая от вершины, лежат на одной сфере, центр которой расположен на прямой Эйлера (сфера Эйлера).
Если точка B1 делит отрезок AH в соотношении 2:1, то
а если M1 — центроид грани A2A3A4, то согласно №366
Аналогично находим остальные векторы
В №814 доказано, что все произведения
3, 4, i≠j, равны между собой. Поэтому после раскрытия скобок получим
следовательно, все точки Мi и Bi лежат на сфере с центром Q.
то М1 и В1 — концы диаметра этой сферы; так как В1 и H лежат на высоте A1H1, а H1 и М1 — на перпендикулярной ей грани А2А3А4 то В1Н1М1 и H1 лежит на сфере. Аналогично на сфере лежат и точки H2, H3, H4.