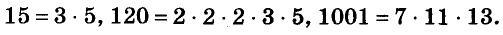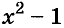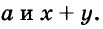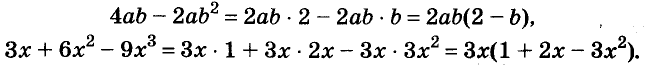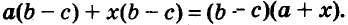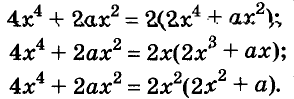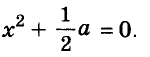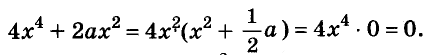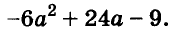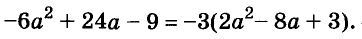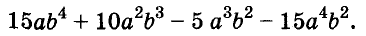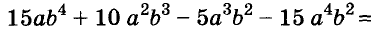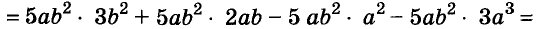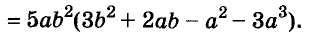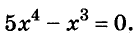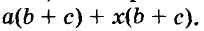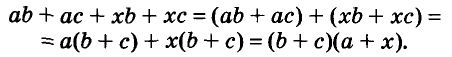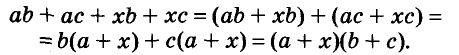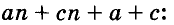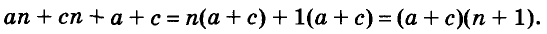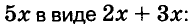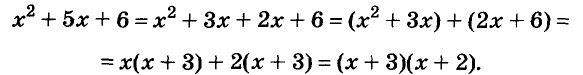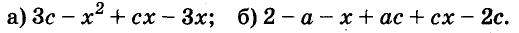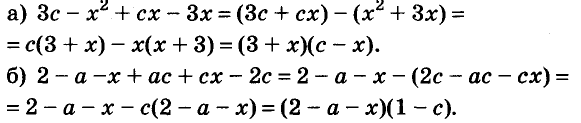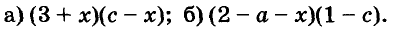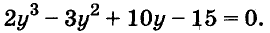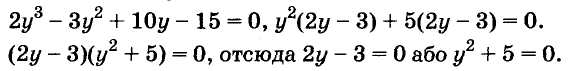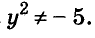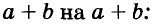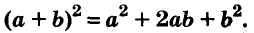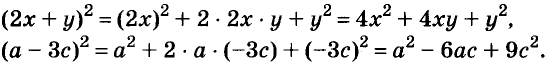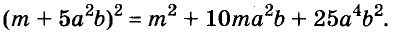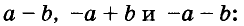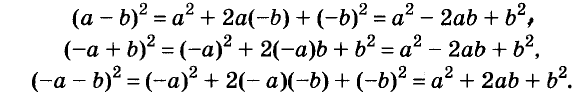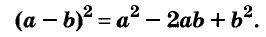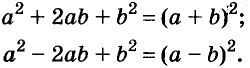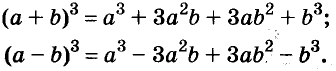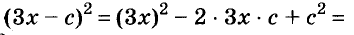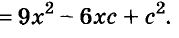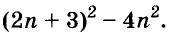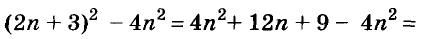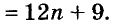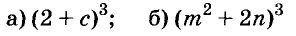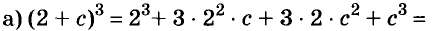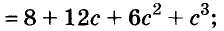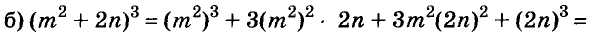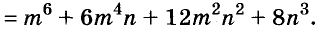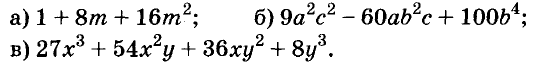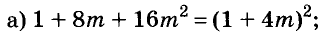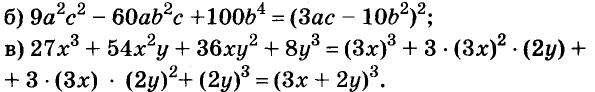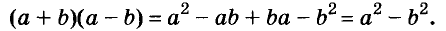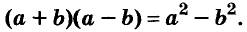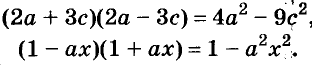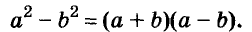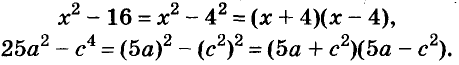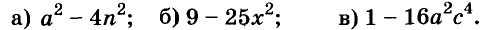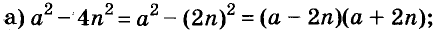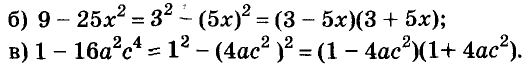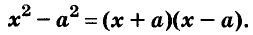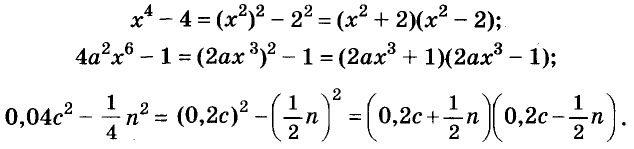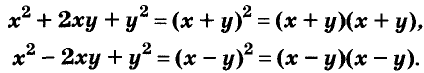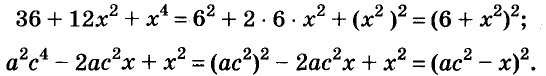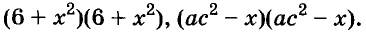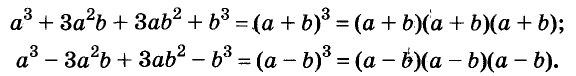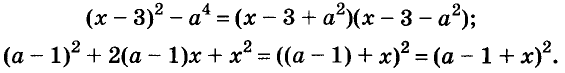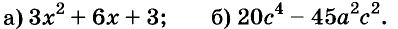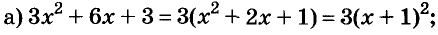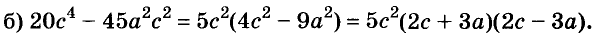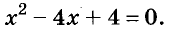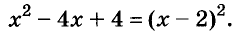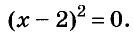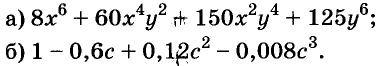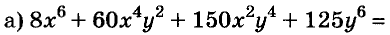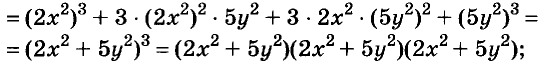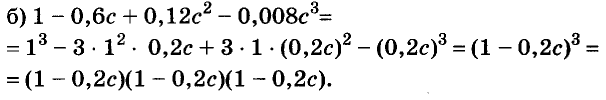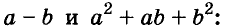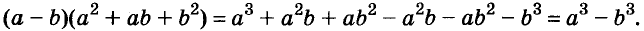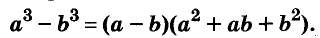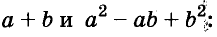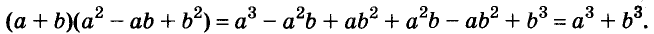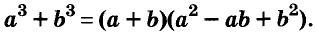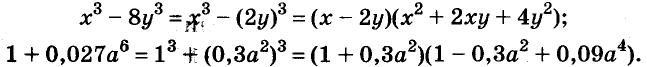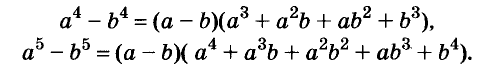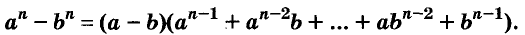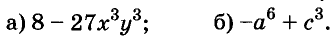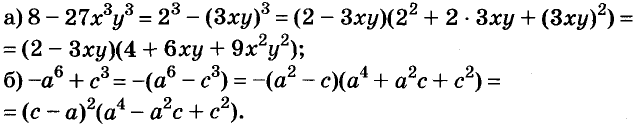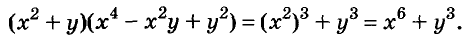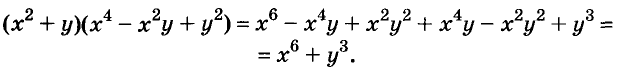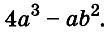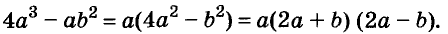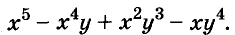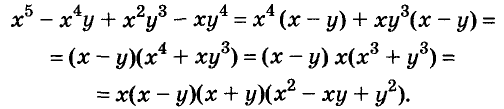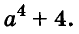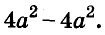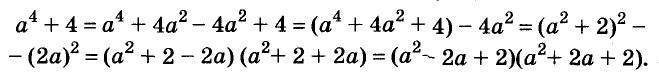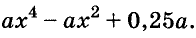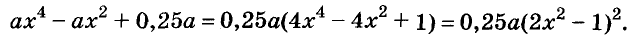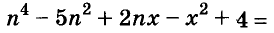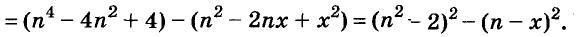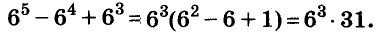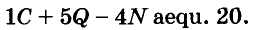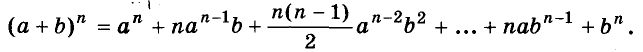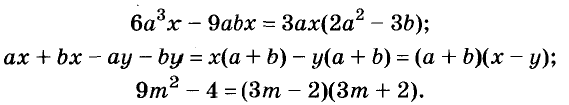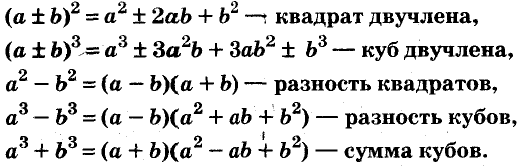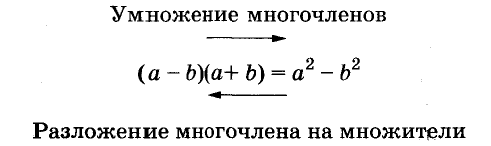Докажите что многочлен представим в виде суммы квадратов двух многочленов

Представление чисел суммой двух квадратов и эллиптические кривые

Совсем легко понять, почему 3, 7, 11 и прочие числа, дающие при делении на 4 остаток 3, непредставимы в виде a 2 +b 2 : квадрат чётного числа всегда делится на 4, квадрат нечётного числа всегда даёт остаток 1 при делении на 4, сумма двух квадратов при делении на 4 может давать остатки 0, 1 или 2, но никак не 3. Представимость простых чисел вида 4k+1 неочевидна (особенно если заметить, что простота существенна: число 21 хотя и имеет нужный остаток, но суммой двух квадратов не представляется).

Вычеты

Натуральных чисел бесконечно много. Бывает полезно объединять их в классы по каким-нибудь признакам. В частности, объединение по остатку от деления на какое-нибудь число n приводит к вычетам по модулю n: вычет x̅ — это класс всех чисел, которые при делении на n дают тот же остаток, что и x. Что эквивалентно, вычет x̅ состоит из всех чисел вида x+n∙k, где k целое. В рамках данного поста все вычеты будут по модулю p (того самого нечётного простого числа из введения). Естественно, различных вычетов столько же, сколько может быть остатков от деления на p, то есть ровно p. По сравнению с бесконечностью натуральных чисел переход к вычетам сильно сокращает число вариантов.
Операции над классами далеко не всегда имеют смысл. Например, попытка сложить класс простых чисел с классом составных чисел не очень осмысленна: мы умеем складывать только числа, а у суммы простого числа и составного числа не видно свойств, общих для класса. Хотя члены клуба тавтологии и могут сказать, что сложение класса простых чисел и класса составных чисел даёт класс чисел, раскладывающихся в сумму простого числа и составного числа.

Для вычетов, тем не менее, сложение, вычитание и умножение, «унаследованные» от натуральных чисел, дают другие вычеты. Например, 2̅+3̅=5̅: возьмём любое число с остатком 2, любое число с остатком 3, и их сумма обязательно даст остаток 5. Вообще говоря, произведение двух ненулевых вычетов по произвольному модулю может внезапно оказаться нулём, 2̅∙3̅=0̅ по модулю 6, что неприятно. Но в случае простого модуля, очевидно, такого не бывает, как говорят, нет делителей нуля. Кроме того, можно решить уравнение a̅∙x̅=b̅ (операция деления) для любых двух вычетов, кроме случая a̅=0̅, и результат будет однозначно определён. Однозначность следует из того, что произведение ненулевых вычетов ненулевое. Поскольку a̅≠0̅, то наибольший общий делитель a и p равен 1 (здесь тоже нужна простота p), расширенный алгоритм Евклида найдёт x и y такие, что a∙x+p∙y=1, откуда следует a̅∙x̅=1̅, а значит, a̅∙(b̅∙x̅)=b̅.

Важное следствие из отсутствия делителей нуля: ненулевой многочлен от одной переменной степени n не может иметь более n корней. (Это хорошо известно для обычных целых чисел, но при использовании операций над вычетами требует дополнительного обоснования: уравнение 3̅∙x̅=0̅ по модулю 6 имеет три решения 0̅, 2̅, 4̅.) Действительно, обычное деление «в столбик» показывает, что любой многочлен f(x) можно представить в виде f(x)=(x-с)g(x)+(некоторая константа), где многочлен g(x) имеет степень на единицу меньше; если c — это корень f(x), то константа равна нулю (подставим x=c); если c’ — другой корень f(x), то он будет корнем g(x) (здесь важно отсутствие делителей нуля), так что процесс можно продолжить. Если уже набралось n корней, то оставшийся g(x) будет константой, причём ненулевой (иначе f(x)=0) и больше корней не имеет.

Вычеты по простому модулю можно складывать, вычитать, умножать. На ненулевые вычеты можно делить. Все эти операции обладают обычными свойствами типа a̅∙b̅=b̅∙a̅. В умных книгах говорят, что вычеты по простому модулю образуют поле (а вычеты по составному модулю, где делить нельзя, а всё остальное такое же, — коммутативное кольцо). И не надо быть умной книгой, чтобы назвать это поле конечным. Поле вычетов — не единственное конечное поле, но другие конечные поля нам не понадобятся.

Чуть-чуть про эллиптические кривые

Квадратичные вычеты и невычеты

Теперь мы готовы предъявить обещанные формулы для компонентов разложения p в сумму двух квадратов. Теорема. Пусть g — любой квадратичный невычет. Если p при делении на 4 даёт остаток 1, то

причём число в первой скобке целое нечётное, число во второй скобке целое чётное. Если же p при делении на 4 даёт остаток 3, то обе суммы в скобках нулевые (а значит, число точек на эллиптических кривых равно p+1).

Доказательство

Поскольку пост и без того длинный, доказательство убрано под спойлер. Его можно спокойно пропустить без ущерба для восприятия.

Если взять ненулевой вычет c и умножить его на все вычеты от 1̅ до p̅-1̅, все произведения будут ненулевыми и попарно различными (если c∙x=c∙y, то c∙(x-y)=0̅, что при ненулевом c может быть только если x=y), а значит, это будет просто какая-то перестановка всех вычетов от 1̅ до p̅-1̅. Следовательно, 1̅∙2̅∙. ∙(p̅-1̅)=(c∙1̅)∙(c∙2̅)∙. ∙(c∙(p̅-1̅))=c p-1 ∙1̅∙2̅∙. ∙(p̅-1̅) и c p-1 =1̅ для любого ненулевого вычета c. (Это было доказательство малой теоремы Ферма.)

Как следствие, получаем .

Если p даёт остаток 1 при делении на 4, то слагаемые с x и -x равны и их сумма четна. Значит, вся сумма также четна и числа в скобках действительно целые. Чётность/нечётность после деления пополам ненамного сложнее: в первой скобке теоремы есть три нулевых слагаемых, остальные слагаемые разбиваются на (p-3)/2 пар с суммой ±2 в каждой паре; при любом знаке при делении на 4 получается остаток 2, вся сумма при делении на 4 даёт остаток такой же, как p-3, то есть 2. После деления пополам получим нечётное число. Во второй скобке теоремы всего одно нулевое слагаемое и (p-1)/2 пар с ±2, итоговый остаток от деления на 4 получается 0, после деления пополам остаётся чётное число.

Пусть p при делении на 4 даёт остаток 1. Обозначим первую скобку теоремы через a, вторую через b. Мы уже знаем, что a и b целые.

Итак, первый способ вычисления даёт

Если x₂/x₁ — квадратичный невычет, то аналогично эллиптическим кривым число решений равно 2p минус число решений в случае квадратичного вычета, то есть 2p-(p-1)=p+1.

Суммируем. Есть один вариант с x₁=x₂=0, дающий p решений. Есть 2(p-1) вариантов, где один из x нулевой, а другой ненулевой, каждый из вариантов даёт p решений. Есть 2(p-1) вариантов с x₂=±x₁, каждый из которых даёт 2p-1 решений. Есть (p-1)((p-1)/2-2) вариантов, где x₁ — произвольный ненулевой вычет, а x₂/x₁ — квадратичный вычет, отличный от ±1̅, каждый из этих вариантов даёт p-1 решений. Наконец, остаётся (p-1) 2 /2 вариантов, где x₁ — произвольный ненулевой вычет, а x₂/x₁ — квадратичный невычет, в каждом из этих вариантов p+1 решений. Итого .

Сравнение двух выражений для N завершает доказательство.

Причём здесь криптография?

Знание числа точек на кривой важно для криптографии на этой кривой. На эллиптической кривой можно ввести операцию сложения точек (о чём слышали, наверное, все, кто хоть что-то знает о криптографии) со специальной точкой O в роли нуля. На основе операции сложения можно определить умножение на натуральное число: 2P=P+P, 3P=P+P+P и так далее. Так вот, можно доказать, что если n — порядок кривой, то nP=O для любой точки P. Зная n, c, d, можно решать уравнения вида x∙(cP)=dP полностью аналогично делению вычетов: расширенный алгоритм Евклида найдёт x, y такие, что c∙x+n∙y=1, откуда x∙(cP)+y∙(nP)=P, то есть x∙(cP)=P. При этом, если c, d неизвестны, а cP и dP заданы координатами, то эффективных методов деления в общем случае неизвестно.

Вычислить число точек на заданной кривой довольно сложно (полиномиальный алгоритм существует, но на практике довольно медленный). Чтобы построить кривую с какими-нибудь свойствами на число точек, можно пытаться взять случайные коэффициенты и вычислять число точек в цикле, пока не получится то, что надо, но придётся подождать. К счастью, есть другой способ.

Источник

Разложение многочленов на множители с примерами решения

Содержание:

Разложение многочленов на множители

Разложение многочленов на множители — операция, об-I ратная умножению многочленов. Как вы уже знаете, решая разные задачи, иногда умножают два или более чисел, а иногда — раскладывают данное число на множители. Подобные задачи возникают и при преобразовании целых алгебраических выражений. В этой главе вы узнаете о:

Вынесение общего множителя за скобки

Вы уже умеете раскладывать на множители натуральные числа. Например,

На множители раскладывают и многочлены. Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену. Например, многочлен

Один из способов разложения многочленов на множители — вынесение общего множителя за скобки. Рассмотрим его.

Каждый член многочлена ах + ау имеет общий множитель а. На основании распределительного закона умножения 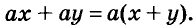Это означает, что данный многочлен ах + ау разложен на два множителя:

Чтобы убедиться, правильно ли разложен многочлен на множители, нужно выполнить умножение полученных множителей. Если всё верно, то в результате должен получиться данный многочлен.

Один и тот же многочлен можно разложить на множители по-разному. Например,

Как правило, стараются вынести за скобки такой общий множитель, чтобы в скобках осталось простейшее выражение. Поэтому чаще всего в качестве коэффициента общего множителя берут наибольший общий делитель (НОД) коэффициентов всех членов данного многочлена или их модулей. Но не всегда. Все зависит от того, с какой целью раскладывают на множители многочлен.

Пусть, например, надо найти значение выражения 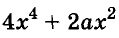при условии, когда

Чтобы использовать условие, это упражнение можно решить так:

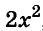
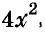
Здесь вынесено за скобки не , а тогда в скобках имеем выражение, значение которого известно из условия.

Пример:

Разложите на множители многочлен

Решение:

или

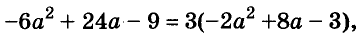
Пример:

Разложите на множители многочлен

Решение:

Пример:

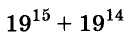
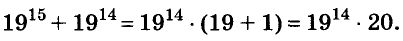
Докажите, что число делится на 20.

Последнее произведение делится на 20, поэтому делится на 20 и данная сумма.

Пример:

Решите уравнение

Решение:

поэтому данное уравнение равносильно уравнению Произведение двух чисел равно нулю тогда, когда хотя бы одно из них равно нулю.

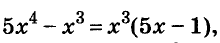
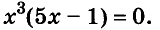
Ответ. Уравнение имеет два корня: 0 и 0,2.

Способ группировки

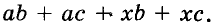
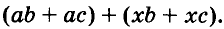
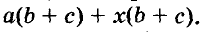
Разложим на множители многочлен Сгруппируем его члены так, чтобы слагаемые в каждой группе имели общий множитель Вынесем из первой группы за скобки общий множитель а, из второй — общий множитель х, получим выражение Слагаемые этого выражения имеют общий множитель b + с, вынесем его за скобки, получим выражение

Указанные преобразования можно записать цепочкой:

Такой способ разложения многочленов на множители называют способом группировки.

Замечание. Раскладывая на множители представленный выше многочлен, можно сгруппировать его члены иначе:

Получили такой же результат.

Разложим на множители многочлен

Записывать сумму а + с в виде 1 (а + с) необязательно, но сначала, чтобы не допускать ошибок, можно писать и так.

Чтобы воспользоваться способом группировки, иногда приходится один член данного многочлена представлять в виде суммы или разности одночленов. Чтобы разложить на множители трёхчлен 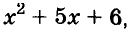• запишем одночлен

Подобные преобразования также можно выполнять, используя тождества.

Пример:

Разложите на множители многочлен:

Решение:

Ответ.

Пример:

Решите уравнение:

Решение:

Разложим левую часть уравнения на множители:

Корнем первого уравнения является у = 1,5, а второе уравнение корней не имеет, так как

Квадрат двучлена

Решая различные задачи, часто приходится умножать двучлены вида 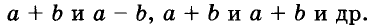Чтобы в таких случаях можно было сразу написать ответ, полезно запомнить тождества, которые называют формулами сокращённого умножения. Рассмотрим некоторые из них.

Умножим двучлен

Следовательно,

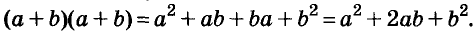
Квадрат двучлена равен квадрату первого его члена плюс удвоенное произведение первого на второй плюс квадрат второго члена.

Доказанное равенство — тождество, его называют формулой квадрата двучлена. Пользуясь ею, можно сразу записать:

Промежуточные преобразования желательно выполнять устно, тем самым сокращается запись:

По формуле квадрата двучлена можно возводить в квадрат любые двучлены, в том числе

Формулы квадрата двучлена используют и в «обратном направлении»:

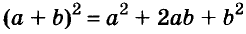
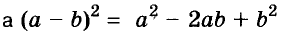
Формулу часто называют формулой квадрата суммы двух выражений, — квадрата разности двух выражений.

Для положительных чисел а и b формулу

можно доказать геометрически, как показано на рисунке 44. Так её доказывали ещё древние греки. Ведь площадь квадрата со стороной а + b равна сумме площадей квадратов а также прямоугольников ab и ab.

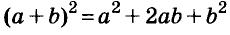
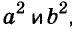
Существуют и другие формулы сокращённого умножения:

Пример:

Возведите в квадрат двучлен

Решение:

Пример:

Упростите выражение

Решение:

Пример:

Представьте в виде многочлена выражение:

Решение:

Пример:

Представьте выражение в виде степени двучлена:

Решение:

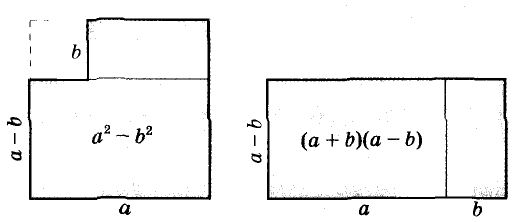
Разность квадратов

Умножим сумму переменных а и b на их разность.

Значит,

Это равенство — тождество. Словами его читают так:

Произведение суммы двух выражений и их разности равно разности квадратов этих выражений.

Пользуясь доказанной формулой, можно сразу записать:

Левую и правую части доказанной формулы можно поменять местами. Получим формулу разности квадратов двух выражений:

Разность квадратов двух выражений равна произведению их суммы и разности.

Пример:

Формула разности квадратов очень удобна для разложения многочленов на множители.

Для положительных чисел а и b формулу 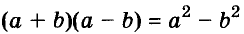можно проиллюстрировать геометрически (рис. 46). Но это тождество верно не только для положительных чисел, но и для любых других чисел и выражений.

Истинность формулы разности квадратов следует из правила умножения многочленов, а это правило — из законов действий сложения и умножения. Законы сложения и умножения чисел — это своеобразные аксиомы, следствиями которых являются алгебраические тождества.

Пример:

Напишите разность квадратов и квадрат разности выражений

Решение:

— разность квадратов; — квадрат разности данных выражений.

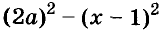
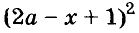
Пример:

Запишите в виде произведения двух двучленов выражение:

Решение:

Пример:

Представьте в виде двучлена выражение:

Решение:

.

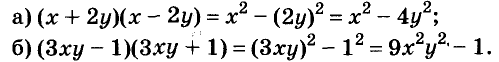
Используя формулу разности квадратов, промежуточные вычисления и преобразования можно выполнять устно, а записывать лишь конечный результат.

Использование формул сокращённого умножения

С помощью формул сокращённого умножения некоторые многочлены можно разложить на множители. Например, двучлен 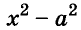можно представить в виде произведения по формуле разности квадратов:

Примеры:

Трёхчлены 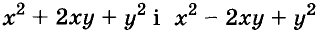раскладывают на множители по формуле квадрата двучлена:

Примеры:

Полученные, выражения можно разложить на множители и записать так:

Многочлен 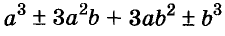можно разложить на множители по формуле куба двучлена:

Раскладывать на множители можно не только многочлены, но и некоторые другие целые выражения.

Например, 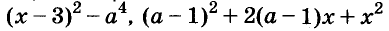— не многочлены, но и их можно представить в виде произведений многочленов:

Пример:

Разложите на множители многочлен:

Решение:

Пример:

Решите уравнение

Решение:

Значит, данное уравнение равносильно такому:

Пример:

Разложите на множители многочлен:

Решение:

Разность и сумма кубов

Выполним умножение многочленов

Следовательно, при любых значениях а и b

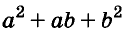
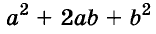
Трёхчлен называют неполным квадратом суммы выражений а и b (от он отличается только коэффициентом среднего члена). Поэтому доказанную формулу словами читают так:

разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

Выполним умножение многочленов

Трёхчлен 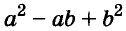называют неполным квадратом разности выражений а и b. Поэтому полученную формулу читаю так:

сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

С помощью доказанных формул можно раскладывать на множители многочлены, являющиеся разностями или суммами кубов.

Примеры:

Формулу «разность кубов» для положительных значений а и b можно проиллюстрировать геометрически, как показано на рисунке 49.

Можно доказать, что для каждого натурального значения n истинна формула:

Формулы «разность квадратов» и «разность кубов» — простейшие случаи этой общей формулы.

Пример:

Разложите на множители двучлен:

Решение:

Пример:

Найдите произведение многочленов: •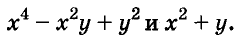

Решение:

Первый способ. По формуле суммы кубов:

Второй способ. По правилу умножения многочленов:

Применение разных способов разложения многочленов на множители

Чтобы разложить многочлен на множители, иногда приходится применять несколько способов.

Пример:

Разложите на множители многочлен

Решение:

Сначала за скобки вынесен общий множитель а, потом выражение в скобках разложено на множители по формуле разности квадратов.

Пример:

Разложите на множители выражение

Решение:

Здесь применены способ группировки, вынесение общего множителя за скобки и формула суммы кубов.

Чтобы разложить на множители более сложные многочлены, приходится применять несколько известных способов или искусственные приёмы.

В этом случае можно использовать такое правило-ориентир:

Иногда удаётся разложить многочлен на множители, прибавляя и вычитая из него одно и то же выражение.

Пример:

Разложите на множители двучлен

Решение:

Прибавим к данному двучлену выражение

Пример:

Разложите на множители выражение

Решение:

Пример:

Представьте многочлен 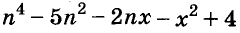в виде разности квадратов двух многочленов.

Решение:

Пример:

Докажите, что число 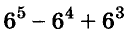делится на 31.

Последнее произведение делится на 31, поэтому делится на 31 и равное ему данное числовое выражение.

Исторические сведения:

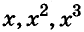
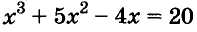
Наибольший вклад в развитие алгебраической символики внёс известный французский математик Ф. Виет, которого называли «отцом алгебры ». Он часто использовал буквенные обозначения. Вместо писал соответственно N,Q,C — первые буквы латинских слов Numerus (число), Quadratus (квадрат), Cubus (куб). Уравнение Ф. Виет записывал так:

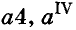
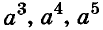
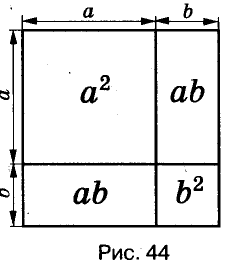
Степени чисел продолжительное время не имели специальных обозначений, четвёртую степень числа а записывали в виде произведения аааа. Позднее такое произведение начали записывать . Записи предложил Р. Декарт.

Формулы сокращённого умножения древним китайским и греческим математикам были известны за много веков до начала нашей эры. Записывали их тогда не с помощью букв, а словами и доказывали геометрически (только для положительных чисел). Пользуясь рисунком, объясняли, что для любых чисел а и b площадь квадрата со стороной а + b равна сумме площадей двух квадратов со сторонами а и b к двух прямоугольников со сторонами а, b. Итак, 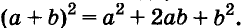Подобным способом обосновали и другие равенства, которые. мы теперь называем формулами сокращённого умножения.

В учебнике рассмотрены простейшие формулы сокращённого умножения.

Формулы квадрата и куба двучлена — простейшие случаи общей формулы бинома Ньютона:

Напомню:

Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену.

Простейшие способы разложения многочленов на множители:

Примеры:

Формулы сокращённого умножения

Разложение многочленов на множители — это преобразование, обратное умножению многочленов. Схематично эти две операции можно изобразить, например, так.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник