Докажите что объемы двух цилиндров у которых площади боковых поверхностей равны
Цилиндр
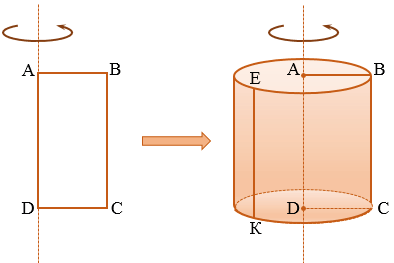
Тела вращения – это объемные тела, которые возникают при вращении некой плоской фигуры, которая ограничена кривой и крутится вокруг оси, лежащей в той же плоскости. К телам вращения относятся цилиндр, конус и шар.
Возьмем прямоугольник АВСD. Будем вращать этот прямоугольник против часовой стрелки вокруг стороны АD.
Определение
Объем цилиндра
| Объем цилиндра равен произведению площади основания на высоту. |
Доказательство:
Дано: цилиндр с площадью основания S, высотой h и объемом V.
Доказать: V = Sh.
Доказательство:
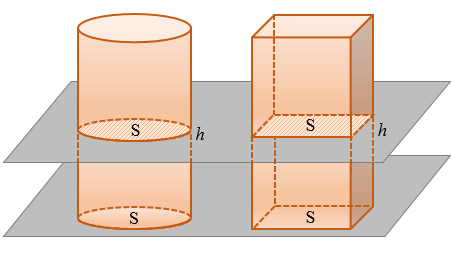
Воспользуемся принципом Кавальери. Рассмотрим цилиндр и призму с площадями оснований, равными S, и высотами, равными h, «стоящие» на одной плоскости.
Площадь боковой поверхности цилиндра
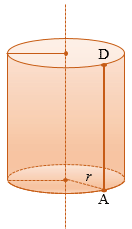
Рассмотрим цилиндр с радиусом r и высотой h.
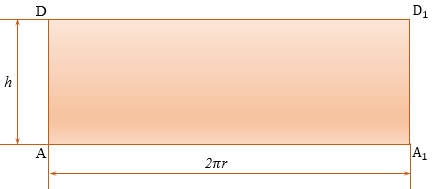
Представим, что его боковую поверхность разрезали по одной из его образующих АD и развернули так, что получился прямоугольник АDА1D1, стороны АD и А1D1 которого являются двумя краями разреза боковой поверхности цилиндра. Этот прямоугольник называется разверткой боковой поверхности цилиндра.
Сторона АА1 прямоугольника АDА1D1 равна длине окружности основания, а сторона АD равна высоте цилиндра, т.е. АА1 = 2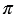
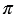
Площадь Sбок боковой поверхности цилиндра равна площади ее развертки, т.е. Sбок = 2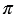 rh. rh. |
Поделись с друзьями в социальных сетях:
Задачи егэ боковая поверхность цилиндр
Задачи для подготовке к ЕГЭ по теме: «Цилиндр. Площадь поверхности цилиндра»
Ищем педагогов в команду «Инфоурок»
Задачи для подготовки к ЕГЭ
» Цилиндр. Площадь поверхности цилиндра»
№2 Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
№4 Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
№6 Радиус основания цилиндра равен 26, а его образующая равна 9. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 24. Найдите площадь этого сечения.
№7 Даны два цилиндра. Радиус основания и высота первого равны соответственно 4 и 18, а второго — 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
№2 Длина окружности основания цилиндра равна 3, высота равна 4. Найдите площадь боковой поверхности цилиндра.
№4 Длина окружности основания цилиндра равна 14. Площадь боковой поверхности равна 182. Найдите высоту цилиндра.
№5 Площадь боковой поверхности цилиндра равна 21, а диаметр основания равен 7. Найдите высоту цилиндра.
№6 Радиус основания цилиндра равен 13, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.
№7 Даны два цилиндра. Радиус основания и высота первого равны соответственно 2 и 3, а второго — 12 и 5. Во сколько раз площадь боковой поверхности второго цилиндра больше площади боковой поверхности первого?
Задачи егэ боковая поверхность цилиндр
Даны два цилиндра. Радиус основания и высота первого равны соответственно 2 и 6, а второго — 6 и 7. Во сколько раз объём второго цилиндра больше объёма первого?
Объём цилиндра находится по формуле:
Найдём объём первого цилиндра:
Найдём объём второго цилиндра:
Найдём отношение объёма второго шара к первому:
Радиус основания цилиндра равен 26, а его образующая равна 9. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 24. Найдите площадь этого сечения.
Даны два цилиндра. Радиус основания и высота первого равны соответственно 4 и 18, а второго — 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
Площадь боковой поверхности цилиндра находится по формуле:
Найдём площадь боковой поверхности первого цилиндра:
Найдём площадь боковой поверхности второго цилиндра:
Найдём отношение площади боковой поверхности цилиндра первого цилиндра ко второму:
Радиус основания цилиндра равен 13, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно
Даны два шара с радиусами 9 и 3. Во сколько раз площадь поверхности большего шара больше площади поверхности меньшего?
Сечение, параллельное оси цилиндра, — прямоугольник. Одна его сторона равна образующей цилиндра. Найдем вторую его сторону из прямоугольного треугольника в основании по формуле: где AB — данная сторона, r — радиус основания цилиндра, аh — расстояние от сечения до оси цилиндра. Таким образом, площадь данного сечения равна 18 · 10 = 180.
В основании правильной четырехугольной пирамиды лежит квадрат. Где СH — половина его диагонали: а его площадь равна
По теореме Пифагора находим высоту данной пирамиды
Отсюда ее объем равен:
Площади шаров относятся как квадраты их радиусов, следовательно, площадь второго шара в раз больше площади первого.
Задачи егэ боковая поверхность цилиндр
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Если сначала найти объем целого цилиндра, то он равен 1/3 * ПИ * r^2 * H, где r=6, H=5, то есть объем цилиндра равен 60 пи, а потом разделить его на четыре, т.к. данный сектор занимает 1/4 части всего цилиндра, то получится 15. В чем дело, что не так?
Ошибка в формуле. Объём цилинлра равен произведению высоты на площадь основания.
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной фигуры равен сумме объемов цилиндра с радиусом основания 2 и высотой 3 и половины цилиндра с тем же радиусом основания и высотой 1:
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной фигуры равен сумме объемов цилиндра с радиусом основания 2 и высотой 3 и половины цилиндра с тем же радиусом основания и высотой 1:
Добрый день,в условии указано что первая высота равна 3, а вторая 1. Почему в решении написано 0,5H(2)?
Так учитывается половина цилиндра
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной фигуры равен разности объемов цилиндра с радиусом основания 5 и высотой 5 и цилиндра с той же высотой и радиусом основания 2:
Задачи егэ боковая поверхность цилиндр
Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.
Высота цилиндра равна диаметру шара, а радиус основания цилиндра равен радиусу шара (см. рис.).
Площадь основания цилиндра:
Площадь боковой поверхности цилиндра:
Площадь полной поверхности цилиндра:
Поскольку площадь поверхности шара дается формулой имеем:
Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна Найдите площадь боковой поверхности конуса.
Заметим, что конус и цилиндр имеют общую высоту и равные радиусы основания. Площадь боковой поверхности цилиндра равна откуда, учитывая, что
получаем:
или
Образующая конуса его высота
и радиус основания
связаны соотношением
откуда, учитывая, что
получаем:
или
Площадь боковой поверхности конуса равна следовательно:
Цилиндр и конус имеют общее основание, вершина конуса является центром другого основания цилиндра. Каждая образующая конуса наклонена к плоскости основания под углом 30°.
а) Докажите, что площади боковых поверхностей цилиндра и конуса равны
б) Найдите радиус сферы, касающейся боковых поверхностей цилиндра и конуса, а так
же одного из оснований цилиндра, если известно, что объем конуса равен
а) Пусть радиус основания цилиндра равен а высота
Тогда тангенс угла наклона образующей есть
откуда
и образующая конуса равна
Вычислим теперь площади боковой поверхности цилиндра и конуса. Это
и
что и требовалось доказать.
б) Рассмотрим сечение цилиндра и конуса осевой плоскость, проходящей через центр сферы. Все точки касания будут лежать в этой плоскости. В сечении получим окружность, вписанную в прямоугольный треугольник со сторонами
поэтому ее радиус равен
C другой стороны, как мы знаем,
откуда поэтому искомый радиус равен 1.
Как найти площадь поверхности цилиндра: боковую, основания, полную
Площадь боковой поверхности цилиндра
Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:
Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.
Формула площади осевого сечения цилиндра выводится из формулы расчета площади прямоугольника :
Круговой цилиндр
где r – радиус основы, h – высота цилиндра, d – диаметр основы.
Как рассчитать площадь боковой поверхности цилиндра с помощью калькулятора
Калькулятор позволяет определить площадь цилиндра по одному из 2 вариантов исходных данных:
Выберите соответствующий шаг и введите исходные данные в соответствующие поля.
Также важно указать единицы измерения по условиям задачи.
Расчеты будут выполнены автоматически и конвертированы в основные метрические физические величины площади.
Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.
Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.
Осевое сечение прямого цилиндра
Осевым называется любое сечение цилиндра, которое содержит его ось. Это определение означает, что осевое сечение будет всегда параллельно образующей линии.
В цилиндре прямом ось проходит через центр круга и перпендикулярна его плоскости. Это означает, что рассматриваемое сечение круг будет пересекать по его диаметру. На рисунке показана половинка цилиндра, которая получилась в результате пересечения фигуры плоскостью, проходящей через ось.
Не сложно понять, что осевое сечение прямого круглого цилиндра представляет собой прямоугольник. Его сторонами являются диаметр d основания и высота h фигуры.
Запишем формулы для площади осевого сечения цилиндра и длины hd его диагонали:
Прямоугольник имеет две диагонали, но обе они равны друг другу. Если известен радиус основания, то не сложно переписать эти формулы через него, учитывая, что он в два раза меньше диаметра.
Введите радиус основания и высоту цилиндра
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Площадь полной поверхности цилиндра
Для нахождения полной площади цилиндра нужно к полученной Sбок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле Sо = 2π * r2.
Конечная формула выглядит следующим образом:
Sпол = 2π * r2 + 2π * r * h.