Докажите что отношение эквивалентности
MT1102: Линейная алгебра (введение в математику)
Классы эквивалентных элементов и их свойства
Пусть %%R%% — отношение эквивалентности на множестве %%M%% и %%a%% — некоторый элемент из %%M%%. Рассмотрим множество всех элементов из %%M%%, находящихся в отношении %%R%% к элементу %%a%%.
Классом эквивалентности %%M_a%%
называется множество всех элементов %%M%%, находящихся в отношении %%R%% к элементу %%a%%, то есть множество
Пример
Пусть %%M%% — множество всех жителей России и %%R%% — отношение эквивалентности «проживать в одном городе». Найти классы эквивалентных элементов %%M_a%% для %%a \in M%%.
В зависимости от элемента %%a%% получаем несколько классов эквивалентности. Например, класс эквивалентности жителей Москвы или Санкт-Петербурга.
Свойства классов эквивалентности
Пусть %%R%% — отношение эквивалентности на множестве %%M%% и %%M_a, M_b, \dotsc, M_z, \dotsc%% — все классы эквивалентности для отношения %%R%%. Тогда эти классы имеют следующие свойства.
Свойство 1
Действительно, по определению, класс %%M_a = \ a\>%%. Тогда для элемента %%a%% должно выполняться условие %%a \in M_a \leftrightarrow a a%%, которое выполняется в связи с тем, что отношение %%R%% рефлексивно по определению отношения эквивалентности. Следовательно, %%a \in M_a%%. Как следствие этого свойства можно сказать, что всякий класс %%M_a%% является непустым множеством. Совокупностью подмножеств %%M_i%%, где %%i \in I%% (множеству индексов), множества %%M%% называется разбиением множества %%M%% если выполняются следующие условия: Теорема. Пусть %%R%% — отношение эквивалентности на множестве %%M%%. Тогда совокупность классов эквивалентности множества %%M%% образует его разбиение. Действительно, если в качестве подмножеств %%M_i%% взять классы эквивалентности %%M_a%%, то все три условия выполняются: Все условия определения разбиения выполнены. Следовательно классы эквивалентности есть разбиение множества %%M%%. Пусть дано множество %%M = \<1, 2, 3, 4, 5, 6, 7, 8, 9, 0 \>%%, тогда разбиением этого множества могут быть следующие совокупности множеств: Но следующие совокупности не являются разбиением: Совокупность множеств %%C_i%% не является разбиением, т.к. оно не удовлетворяет условию 3 разбиения множеств: множества %%C_1%% и %%C_3%% имеют общий элемент %%3%%. Совокупность множеств %%D_i%% не является разбиением, т.к. оно не удовлетворяет условию 1 разбиения множеств: множество %%D_4%% пусто. Совокупность множеств %%E_i%% не является разбиением, т.к. оно не удовлетворяет условию 2 разбиения множеств: объединение множеств %%E_1, E_2%% и %%E_3%% не образует множество %%M%%. Бинарное отношение называется эквивалентностью, если оно рефлексивно, симметрично и транзитивно. Эквивалентность обозначается символом на множестве А по элементу а называется множество, определенное следующим образом: Разумеется, элемент а, для которого класс эквивалентности определен таким образом, также входит в этот класс в силу рефлексивности отношения эквивалентности. Множество классов эквивалентности связано с разбиением несущего множества. Вообще разбиением множества М называется множество, элементами которого являются множества подмножества М; объединение этих подмножеств равно М, а пересечения попарно пусты. Пустое множество не входит в разбиение. Можно доказать, что отношение эквивалентности “ ” на А образует разбиение А/ множества А, причем элементами разбиения являются классы эквивалентности. Разбиение называется минимальным, если в каждый класс эквивалентности входит по одному элементу. Примером такого отношения является отношение х у Û х=у, х,у Î А. Разбиение называется максимальным, если оно образует единственный класс эквивалентности, в который входят все элементы А. Множество классов эквивалентности элементов множества А по эквивалентности “ ” называется фактор-множеством А по “ Примерами отношений эквивалентности являются отношения равенства чисел (образует максимальное разбиение), конгруэнтности треугольников (классы эквивалентности включают все конгруэнтные треугольники), равенства множеств, равномощности множеств, сравнимости чисел по модулю m (это отношение определяет множества чисел, дающих одинаковый остаток при делении на m). Теорема. Если “ ” – отношение эквивалентности, заданное на произвольном непустом множестве А, то существует разбиение R = y тогда и только тогда, когда х и у принадлежат к одному и тому же классу разбиения. — эквивалентность на А и A/ = . Докажем существование разбиения R , равного фактор множеству A/ · Пусть aÎA – произвольный элемент А. Обозначим Аа = a> – класс эквивалентности по элементу а. Тогда аÎАа, и, следовательно · Докажем теперь, что попарные пересечения классов эквивалентности пусты. Пусть a,b Î A, aÎ Aa, b Î Ab, Aa и Ab –два класса эквивалентности. Пусть Аa Ç Ab ¹Æ. Тогда существует хотя бы один элемент сÎА такой, что с Î Аa и с Î Аb, т.е. с b. Пусть z – произвольный элемент множества Аа. Тогда z с. По свойству транзитивности отношения эквивалентности получаем z b, следовательно, по свойству транзитивности z b. Следовательно, z Î Ab. Следовательно, Aa Í Ab. Обратное включение доказывается аналогично. Следовательно, пересечение Aa и Ab не пусто тогда и только тогда, когда это одно и то же множество. Таким образом, доказано, что множество классов эквивалентности образуют разбиение множества А. ¨ Таблица 2 Свойства отношения эквивалентности Определение. Бинарное отношение, являющееся одновременно рефлексивным, симметричным и транзитивным, называется Отношением эквивалентности. Если R является отношением эквивалентности, то часто вместо ARb пишут A b, если ясно, о каком отношении эквивалентности R идет речь. Примеры Отношений эквивалентности. 1. Отношения подобия треугольников. 2. Отношение тождества на множестве алгебраических выражений. 3. Отношение параллельности на множестве прямых. 4. Отношение учиться в одной группе на множестве студентов. 5. Отношение получить одну и ту же оценку по математике на экзамене. 6. Отношение иметь одинаковый остаток при делении на 7 на множестве 7. На множестве комплексных чисел С отношение иметь одинаковый модуль: z1 Контрпримеры (отношения, не являющиеся отношениями эквивалентности). 1. 2. 3. Отношение Определение. Пусть на множестве А задано отношение эквивалентности и A Свойства классов смежности. 1. a, ввиду рефлективности). Доказательство. Проверим, что [A] b, то по свойству транзитивности X b И, следовательно, X a. Далее, поменяв местами A и B и все повторив, получим [B] Замечание. Свойство 2 означает, что любой класс смежности однозначно определяется любым своим представителем. Тем самым, все представители класса равноправны при определении этого класса. 3. Любые два класса эквивалентности либо не пересекаются, либо совпадают. Доказательство. Пусть C [C] Определение. Совокупность всех различных смежных классов множества А по отношению эквивалентности Замечание. Свойство 3 показывает, что такая совокупность всех различных смежных классов (фактор—множество) представляет собой некоторое разбиение множества А. Обратно, всякое разбиение множества А=А1 Действительно, если задано разбиение множества A (такое, как выше), то положим A b, если a и B принадлежат одному и тому же подмножеству Ai (рефлексивность и симметричность очевидны, транзитивность легко следует из того, что Ai Формальная теория моделирования использует алгебраические отношения, включая их в сигнатуры моделей алгебраических структур, которыми описывает реальные физические, технические объекты и процессы их функционирования. Эта публикация является продолжением предшествующей, прочтение которой желательно, так как многие понятия и термины, используемые здесь, описываются там. Предлагается изложение не в традиционном (стрелочном) стиле, а так, как мне самому пришлось всю эту кухню представлять и осваивать и по учебникам/пособиям, и по журнальным статьям. Особенно полезной вещью считаю созданный мной каталог, он позволяет выделить практически любое пространство и представить его элементы в удобном виде: матрицей, графом и др. Сразу видишь с чем имеешь дело и свойства (они уже выписаны) проверять часто не требуется. Думаю, что термин отношение знаком каждому читателю, но просьба дать определение поставит большинство в тупик. Причин для этого много. Они чаще всего в преподавателях, которые, если и использовали отношения в процессе преподавания, внимания на этом термине не заостряли, запоминающихся примеров не приводили. Некоторые комментаторы статьи отнесли замечания на свой счет и насыпали минусов. Но шила в мешке не утаишь. Серьезных публикаций как не было, так и нет. Задайте себе вопрос, работали ли Вы с каким-либо пространством отношений? И честно себе ответьте. Что об этом пространстве можете миру поведать, для начала хотя-бы перечислить его элементы и указать свойства. Даже на СУБД Вы смотрите глазами их создателей, а они ведь тоже не все видят, или не все показывают, как, например, в микросхемах. Здесь сделаю небольшой повтор. Начинать следует с абстрактного множества А = Отношения можно задавать в разном представлении: Пространством бинарных отношений с множеством-носителем называется произвольное подмножество множества бинарных отношений заданных на. Рассмотрим основные пространства для отношений предпочтений (рис. 2.15). Рисунок 2.15 Схема пространств бинарных отношений Выявленные связи между пространствами используются для переноса задач принятия решений (ЗПР) из одних пространств в другие, где они могут быть решены более простым путем, а затем полученное решение возвращают в исходное пространство, где была сформулирована ЗПР. Определение. Бинарное отношение σ ⊆ А×А, обладающее тремя свойствами рефлексивности, симметричности, транзитивности, называется, бинарным отношением эквивалентности (БОЭ). Обозначается отношение эквивалентности σ(х, у), (х, у)∊σ, хσу, х≈у. Удобно использовать матричное (табличное) представление отношения. Ниже на рис 2.24 приведено как раз матричное представление. Над множеством из 4-х элементов существует 15 БОЭ, которые все изображены. Представление и анализ структуры отношений эквивалентности (n = 4) Начнем с примера об эквивалентностях, который иллюстрирует ограниченность их количества. Пример 1. Пусть имеется три кубика. Составим список свойств, которыми наделены кубики и практическое использование которых (свойств кубиков) делает их как бы взаимозаменяемыми. Кубикам присвоим номера, а их свойства представим таблицей 1. По каждому из свойств возникает БОЭ и классы эквивалентности. Продолжая список свойств, мы новых отношений эквивалентности не получим. Будут только повторы уже построенных, но для других признаков. Покажем связь БОЭ с множествами. Рассмотрим множество из трех элементов А = <1,2,3>и получим для него все возможные разбиения на все части. ①1|2|3; ②12|3; ③13|2; ④ 1|23; ⑤123. Последнее разбиения на одну часть. Номера разбиений и БО в кружках. Определение. Разбиением множества А называют семейство Аi, i = 1(1)I, непустых попарно непересекающихся подмножеств из А, объединение которых образует все исходное множество А=UАi, Аi∩Аj =∅, ∀ i ≠ j. Под-множества Аi называют классами эквивалентности разбиения исходного множества. Это все разбиения множества (5 штук). Анализ БО показывает, что различных отношений эквивалентности тоже только 5 штук. Случайно ли это совпадение? Мы можем каждому разбиению сопоставить матрицу из девяти ячеек (3×3 = 9), в каждой из которых либо размещается упорядоченная пара элементов из множества А, либо ячейка остается пустой, если для соответствующей пары нет объекта. Строки и столбцы матрицы размечаются элементами множества А, а пересечению строка – столбец соответствует упорядоченная пара (i, j). В ячейку матрицы вписывается не пара, а просто единица или нуль, впрочем, нуль часто не пишут совсем. Нет, совпадение не случайное. Оказывается, каждому разбиению множества взаимно однозначно соответствует БОЭ, при этом мощность множества может быть любой |A| = n. Это отношение едва ли не самое частое по использованию в научном обороте, но совокупность свойств, реализуемых в этом отношении, сильно ограничивает его распространенность. Для |A| = 4 отношений существует 2 16 = 65536, но эквивалентностей лишь 15 штук. Это весьма редкий тип отношений. С другой стороны, отношения эквивалентности широко распространены в прикладных задачах. Везде, где имеются и рассматриваются множества самых различных объектов и различные разбиения таких множеств (не чисел) на части возникают отношения эквивалентности. Их можно назвать математическими (алгебраическими) моделями таких разбиений, классифицирующими множества объектов по различным признакам. Решетка Р(4): все разбиения множества А = Минимальному разбиению соответствует отношение эквивалентности П15, которое называется равенством или единичным отношением. В каждом классе эквивалентности — единственный элемент. Разбиению множества А, включающему лишь само множество А, соответствует отношение эквивалентности, содержащее все элементы декартова квадрата А×А. Ближайший тип к отношениям эквивалентности – отношения толерантности. Множество отношений толерантности содержит в себе все отношения эквивалентности. Для носителя А из трех элементов толерантностей 8. Все они обладают свойствами рефлексивности и симметричности. При выполнении свойства транзитивности пять из восьми толерантностей преобразует в эквивалентности (рис. 2.24 и 2.25). Определение. Совокупность классов [a]σ эквивалентности элементов множества А называется фактор-множеством (обозначается А/σ) множества А по эквивалентности σ. Определение. Естественным (каноническим) отображением f: A→ А/σ называется такое отображение f, при котором f(а) = [a]σ. Об этих БО ранее уже упоминалось, а здесь рассмотрим их подробнее. Всем известны понятия сходство, похожесть, одинаковость, неразличимость, взаимозаменяемость объектов. Они кажутся близкими по содержанию, но при этом не одно и то же. Когда для объектов указано только сходство, то невозможно разбить их на четкие классы так, что внутри класса объекты похожи, а между объектами разных классов сходства нет. В случае сходства возникает размытая ситуация без четких границ. С другой стороны, накапливание несущественных различий у сходных объектов может привести к совершенно непохожим объектам. В предыдущей части мы обсудили содержательный смысл отношения одинаковости (эквивалентности) объектов. Не менее важной является ситуация, когда приходится устанавливать сходство объектов. Пусть изучается форма геометрических тел. Если одинаковость формы объектов, например, кубиков, означает их полную взаимозаменяемость в определенной ситуации обучения, то сходство – это частичная взаимозаменяемость, (когда среди кубиков встречаются очень похожие на них параллелепипеды) т. е. возможность взаимной замены с некоторыми (допустимыми в данной ситуации) потерями. Наибольшая мера для сходства – неразличимость, а вовсе не одинаковость, как может показаться на первый взгляд. Одинаковость – свойство качественно иное. Одинаковость можно рассматривать только как частный случай неразличимости и сходства. Все дело в том, что неразличимые объекты (так же, как и сходные, похожие) не удается разбить на классы так, чтобы в каждом классе элементы не различались, а элементы разных классов заведомо различались. В самом деле, будем рассматривать множество точек (х, у) на плоскости. Пусть величина d имеет значение меньшее порога разрешимости глаза, т. е. d – такое расстояние, при котором две точки, находящиеся на этом расстоянии, сливаются в одну, т.е. визуально неразличимы (при выбранном удалении плоскости от наблюдателя). Рассмотрим теперь n точек, лежащих на одной прямой и отстоящих (каждая от соседних) на расстоянии d. Каждая пара Традиционный подход к изучению сходства или неразличимости состоит в том, чтобы сначала определить меру сходства, а затем исследовать взаимное расположение сходных объектов. Английский математик Зиман, изучая модели зрительного аппарата, предложил аксиоматическое определение сходства. Тем самым свойства сходства стало возможным изучать независимо от того, как конкретно оно задано в той или иной ситуации: расстоянием между объектами, совпадением каких-то признаков или субъективным мнением наблюдателя. Определение. Отношение Т на множестве M называется отношением толерантности или толерантностью, если оно рефлексивно и симметрично. Корректность такого определения видна из того, что объект заведомо неразличим сам с собой и, конечно, похож на себя (это задает рефлексивность отношения). Порядок рассмотрения двух объектов не влияет на окончательный вывод об их сходстве или несходстве (симметричность). Ясно также, что поскольку одинаковость есть частный случай сходства, то эквивалентность должна быть частным случаем толерантности. Сравнивая определения эквивалентности и толерантности, убеждаемся, что так оно и есть. Философский принцип: «частное богаче общего» наглядно подтверждается. Дополнительное свойство – транзитивности делает часть отношений толерантности эквивалентностями. Двое близнецов бывают настолько одинаковыми, что без риска могут сдавать экзамены друг за друга. Однако если два студента только похожи, то такая проделка, хотя и осуществима, но рискованна. Каждый элемент множества несет определенную информацию о похожих на него элементах. Но не всю информацию, как в случае одинаковых элементов. Здесь возможны разные степени информации, которую один элемент содержит относительно другого. Рассмотрим примеры, где толерантность задается разными способами. Пример 2. Множество M состоит из четырехбуквенных русских слов — нарицательных существительных в именительном падеже. Будем называть такие слова сходными, если они отличаются не более чем на одну букву. Известная задача «Превращение мухи в слона» в точных терминах формулируется так. Найти последовательность слов, начинающуюся словом «муха» и кончающуюся словом «слон», любые два соседних слова в которой сходны в смысле только что данного определения. Решение этой задачи: муха — мура — тура — тара — кара — каре — кафе — кафр — каюр — каюк — крюк — крок — срок — сток — стон — слон. Толерантность подмножеств (граней) означает наличие у них общих вершин. Определение. Множество M с заданным на нем отношением толерантности τ называется пространством толерантности. Таким образом, пространство толерантности есть пара (M, τ). Пример 4. Пространство толерантности Sp допускает обобщение на бесконечный случай. Пусть H — произвольное множество. Если SH – совокупность всех непустых подмножеств множества H, то отношение толерантности Т на SH задается условием: X Т Y, если X∩Y ≠ ∅. Симметричность и рефлексивность этого отношения очевидны. Пространство SH обозначается и называется «универсальным» пространством толерантности. Пример 6. Рассмотрим пространство толерантности, компоненты которого принимают любые действительные значения. В частности, это множество всех точек x = (a1, a2) декартовой плоскости. Толерантность двух точек означает совпадение у них хотя бы одной координаты. Значит, две толерантные точки находятся либо на общей вертикали, либо на общей горизонтали. Упорядоченные множества – это множества с введенным на нем отношением порядка. Определение. Множество А и бинарное отношение порядка R на нем (≤) называется частично упорядоченным, если для отношения выполнены (как и в БОЭ) три условия (одно условие другое): Элемент х∊А ЧУМ А покрывает элемент у∊А, если х > y и не существует z∊А такого, что х > z > y. Пара элементов х, у∊А называется сравнимой, если х ≥ у или х ≤ у. Если в ЧУМ А всякая пара его элементов является сравнимой, то А называют линейно упорядоченным множеством или цепью. Если же некоторое ЧУМ В состоит лишь из несравнимых друг с другом элементов, то множество В называют антицепью. Цепь в ЧУМ А называется насыщенной, если она не может быть вложена ни в какую другую цепь, отличную от себя. Аналогично определяется насыщенная антицепь. Максимальной цепью (антицепью) называется цепь (антицепь), содержащая максимальное количество элементов. Элемент m ЧУМ А называется минимальным, если в А нет элемента х∊А, отличного от m и такого, что х≤m. Элемент M ЧУМ А называется максимальным, если в А нет элемента х «большего», чем M, отличного от M и такого, что х ≥ M. Элемент у∊А ЧУМ А называется наибольшим, если ∀ х∊ А х ≤ у. Элемент у∊ А ЧУМ А называется наименьшим, если ∀ х∊А х ≥ у. Для наибольшего и наименьшего элементов принято использовать обозначения 1 и 0 соответственно. Их называют универсальными границами. Всякое ЧУМ А имеет не более одного наименьшего и не более одного наибольшего элементов. В ЧУМ А допустимо несколько минимальных и несколько максимальных элементов Транзитивные дуги не изображаются. Уровни диаграммы Хассе содержат элементы одинакового ранга, т.е. связанные с минимальными элементами ЧУМ путями равной длины (по числу дуг). Точной нижней гранью (обозначается infAB) множества В называется элемент х∊А, если х ≤ у для всех у∊В и, если из условия z ≤ у для всех у∊ В вытекает, что z ≤ х. Пример 7. Заданы два конечных числовых множества ЧУМ (А, ≤) представлено рис. 2.26. Совокупность В Δ всех верхних граней для В называется верхним конусом для множества В. Совокупность В ∇ всех нижних граней для В называется нижним конусом для В. Всякое подмножество ЧУМ также является ЧУМ относительно наследованного порядка. Если в множестве существуют наибольший и/или наименьший элементы, то они являются максимальным (минимальным соответственно). Обратное неверно. Булеан обладает единственным наименьшим (Ø) и единственным наибольшим элементами. В приведенном множестве наименьший элемент нуль (0) и он совпадает с единственным минимальным элементом, а наибольшего элемента не существует. Максимальными элементами являются <19, 20, 21>. Точная верхняя грань для B = <6,7,10,11>есть элемент 21 (это наименьший элемент в верхнем конусе). Общая ситуация. Пусть задано множество, мощность которого*******. Из всех бинарных отношений, возможных на этом множестве, выделим бинарные отношения предпочтения и связанные с ними отношения строгих частичных порядков. Частичные порядки отличаются от строгих частичных порядков только тем, что содержат в своем составе дополнительные элементы (в матричном представлении – диагональные) (аi, ai ) = 1, i = 1(1)n, а число тех и других порядков в полном множестве отношений одинаково. До настоящего времени не найдены зависимости (формула, алгоритм), которые позволяли бы подсчитывать и перечислять при любом n число частичных порядков. Разными авторами непосредственным подсчетом определены и опубликованы следующие результаты (табл. 2.12). Вычислительные эксперименты автора позволили получить не только число, но и вид (представление) частичных порядков при разных мощностях множителя-носителя отношений. Принтер задыхался печатая такие огромные списки, но не только красота требует жертв, наука тоже не отказывается от них. В таблице 2.12 показаны: n = |A| – мощность множества-носителя; вторая строка – количество всех бинарных отношений на множестве А; и далее |Ин(n)| – количество классов неизоморфных отношений; Как видим, в таблице для небольших n, например, Г(n=4) имеется всего 219, приводятся данные, значения которых с увеличением n очень быстро растут, что существенно усложняет их количественный (и качественный) непосредственный анализ даже с помощью ЭВМ. Таблица ниже иллюстрирует возможность порождения Г(n=4) всех частичных порядков из пересечения каждого с каждым линейных частичных порядков. Но в этой ситуации возникают избыточные (повторяющиеся), которые при малых n можно отсечь вручную (пересчитать). Получаются 300 матриц, но ЧУМ среди них лишь 219. Общие формулы так и не были получены. На мировом уровне ситуация аналогичная, хотя мне не довелось видеть публикаций о перечислениях ЧУМ западных авторов. Наши алгоритмы вполне оригинальны и пионерские. Приведу возможную схему решения задачи перечисления элементов пространства частичных порядков (n=4). Множество строгих частичных порядков при лексикографическом упорядочении линейных порядков (n=4) порождается при их взаимном пересечении. Несколько важных определений математики, для встречающихся часто в текстах понятий. Определение. Замкнутый интервал – это множество вида Свойство 2
Свойство 3
Свойство 4
Разбиение множества
Примеры
Отношение эквивалентности



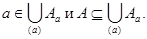
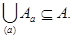
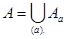
1.4.3. Отношения эквивалентности






















Отношения. Часть II
Понятие отношения
А×А=<(a1, a1),(a1, а2),(a1, a3),(a2, а1),(a2, a2),(a2, a3),(a3, a1),(a3, a2),(a3, a3)>.
Получили 9 упорядоченных пар элементов из А×А, в паре первый элемент из первого сомножителя, второй — из второго. Теперь попробуем получить все подмножества из декартова квадрата А×А. Подмножества будут содержать разное количество пар: одну, две, три и так до всех 9 пар, включаем в этот список и пустое множество ∅. Сколько же получилось подмножеств? Много, а именно 2 9 = 512 элементов.Пространства бинарных отношений
Эти отношения представлены диаграммой на рис. 2.14. Пространства бинарных отношений (типы отношений) представлены рис. 2.15.Отношения эквивалентности
Эквивалентность из бинарных отношений, пожалуй, самое распространенное БО. Редкая наука обходится без этого понятия, но даже тогда, когда эквивалентности используются в изложении каких-либо вопросов, бывает трудно понять, что в виду имел автор. Даже при корректном определении и перечислении свойств, присущих этому бинарному отношению – трудности восприятия остаются.
Так среди всех абстрактных бинарных отношений над множеством из трех элементов (всего их 2 9 = 512 отношений) только пять являются эквивалентностями — носителями требуемых свойств, менее одного процента.Отношения толерантности и их анализ
соседних точек неразличима, но, если n достаточно велико, первая и последняя точки будут отстоять друг от друга на большое расстояние и заведомо будут различимы.
Введем экспликацию понятия сходства или неразличимости.
Из примера со зрительной неразличимостью точек плоскости видим, что транзитивность толерантности выполняется не для всех пар объектов.Отношения частичного порядка и их анализ
Изображать конечное ЧУМ А удобно диаграммой Хассе, которая представляет собой ориентированный граф, его вершины распределены по уровням диаграммы и соответствуют элементам из А, а каждая дуга направляется вниз и рисуется тогда и только тогда, когда элемент х∊А покрывает элемент у∊А.
Пусть В непустое подмножество ЧУМ А, тогда элемент х∊А называется точной верхней гранью (обозначается supAB) множества В, если х ≥ у для всех у∊В и, если из истинности соотношения z ≥ у для всех у∊В вытекает, что z ≥ х.
А = <0,1,2,…,21>и B = <6,7,10,11>.
|Г(n)| – количество отношений частичного порядка;
|Гн(n)| – количество классов неизоморфны отношений частичного порядка;
|Гл(n)| = n! – количество отношений линейного порядка.




