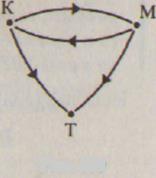
Докажите что отношение r заданное при помощи графа рефлексивно антисимметрично и транзитивно

Упражнения. 1.Докажите, что отношение R, заданное при помощи графа (рис.102), рефлексивно, анти­симметрично и транзитивно

1.Докажите, что отношение R, заданное при помощи графа (рис.102), рефлексивно, анти­симметрично и транзитивно.

2.Докажите, что отношение Т, заданное при помощи графа (рис.103), симметрично и тран­зитивно.

3.Сформулируйте условия, при которых от­ношение свойством рефлексивности не облада­ет, и докажите, что отношение Т (см. упр. 2) не рефлексивно.

4.Сформулируйте условия, при которых от­ношение не обладает свойством: а) симметричности; б) антисимметричности; в)транзитивно­сти; г) связанности.

5.Докажите, что отношение Р, граф которого изображен на рисунке 104, не обладает ни свойством симметричности, ни свойством антисимметричности, ни свойством транзитив­ности.

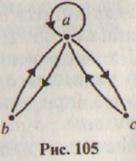
6.Какими свойствами обладает отношение, граф которого изображен на рисунке 105? Яв­ляется ли оно рефлексивным? Транзитивным?

7.Какие из следующих утверждений истинны:

а) Отношение «x больше у на 3» антисимметрично на множестве N, так как из того, что х больше у на 3, не следует, что у больше х на 3.

б) Отношение «x больше у на 3» антисимметрично, так как из того, что х больше у на 3, следует, что у не больше х на 3.

в) Отношение «х больше у на 3» антисим­метрично, так как из того, что х больше у на 3, следует, что у меньше х на 3.

8. На множестве отрезков задано отношение «короче». Верно ли, что оно антисимметрично
и транзитивно? Рефлексивно ли оно?

9. Какими свойствами обладают следующие отношения, заданные на множестве натуральных чисел:

а) «меньше»; б) «меньше на 2»; в) «меньше в 2 раза»?

10. На множестве X =<а, b, с> задано отношение R = <(а, b), (а, а), (b,b), (с, с), (b, а), (b, с), (с, b)>. Какими свойствами оно обладает?

11. На множестве Х= <2,4,6,8, 12>заданы отношения «больше» и «кратно». В чём их сходство и различие?

12.Установите, какое отношение рассматривается в задаче; какие приемы анализа задачи можно использовать:

а) Школьники сделали к карнавалу 15 шапочек для мальчиков, а для девочек в 2 раза больше. Сколько всего карнавальных шапочек они сделали?

б) Второклассники вырезали для елки 26 звездочек, это в 2 раза меньше, чем снежинок. Сколько всего звездочек и снежинок вырезали второклассники?

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Лекция 21. Свойства отношений

1. Свойство рефлексивености

2. Свойство симметричности

3. Свойство транзитивности

Свойства отношений

Мы установили, что бинарное отношение на множестве X пред­ставляет собой множество упорядоченных пар элементов, принад­лежащих декартову произведению X х Х. Это математическая сущ­ность всякого отношения. Но, как и любые другие понятия, отноше­ния обладают свойствами. Их удалось выделить, изучая различные конкретные отношения. Свойств достаточно много, в нашем курсе мы будем изучать только некоторые.

Определение. Отношение R на множестве X называется рефлексив­ным, если о каждом элементе множества X можно сказать, что он находится в отношении R с самим собой.

Используя символы, это отношение можно записать в таком виде:

R рефлексивно на Х ↔ х R х для любого х € X.

Если отношение R рефлексивно на множестве X, то в каждой вер­шине графа данного отношения имеется петля. Справедливо и обрат­ное утверждение: граф, каждая вершина которого имеет петлю, задает отношения, обладающие свойством рефлексивности.

Примеры рефлексивных отношений:

— отношение «кратно» на множестве натуральных чисел (каждое натуральное число кратно самому себе);

— отношение подобия треугольников (каждый треугольник подо­бен самому себе).

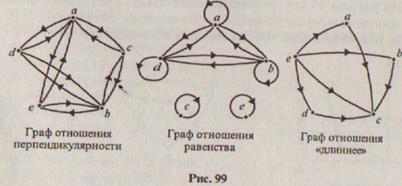
Существуют отношения, которые свойством рефлексивности не обладают. Таким, например, является отношение перпендикулярности на множестве отрезков: нет ни одного отрезка, о котором можно ска­зать, что он перпендикулярен самому себе. Поэтому на графе отноше­ния перпендикулярности (рис. 99) нет ни одной петли. Не обладает свойством рефлексивности и отношение «длиннее» для отрезков.

Обратим теперь внимание на графы отношений перпендикулярно­сти и равенства отрезков. Они «похожи» тем, что если есть одна стрелка, соединяющая пару элементов, то обязательно есть и другая, соединяющая те же элементы, но идущая в противоположном направ­лении. Эта особенность графа отражает те свойства, которыми обла­дают отношения параллельности и равенства отрезков:

— если один отрезок перпендикулярен другому отрезку, то этот «другой» перпендикулярен первому;

— если один отрезок равен другому отрезку, то этот «другой» равен первому.

Про отношения перпендикулярности и равенства отрезков гово­рят, что они обладают свойством симметричности или просто сим­метричны.

Определение. Отношение R на множестве X называется симмет­ричным, если выполняется условие: из того, что элемент х находит­ся в отношении R с элементом у, следует, что и элементу находит­ся в отношении R с элементом х.

Используя символы, это отношение можно записать в таком виде:

R симметрично на Х ↔ (х R y →yRx).

опр.

Граф симметричного отношения обладает особенностью: вместе с каждой стрелкой, идущей от х к у, граф содержит и стрелку, идущую от у к x. Справедливо и обратноеутверждение. Граф, содержащий вместе с каждой стрелкой, идущей от x к у, и стрелку, идущую от у к x, является графом симметричного отношения.

В дополнение к рассмотренным двум примерам симметричных от­ношений присоединим еще такие:

-отношениепараллельности на множестве прямых (если прямая x параллельна прямой у, то и прямая у параллельна прямой х)

-отношение подобия треугольников (если треугольник F подобен треугольнику Р, то треугольник Р подобен треугольнику F).

Существуют отношения, которые свойством симметричности не обладают. Таким, например, является отношение «длиннее» на мно­жестве отрезков. Действительно, если отрезок x длиннее отрезка у, то отрезок у не может быть длиннее отрезка х. Про отношения «длиннее» говорят, что оно обладает свойством антисимметрично­сти или просто антисимметрично.

Определение. Отношение R на множестве X называется анти­симметричным, если для различных элементов х и у из множества X выполнено условие: из того, что х находится в отношении R с элементом у, следует, что элемент у в отношении R с элементом х не находится.

Используя символы, это определение можно записать в таком виде:

R симметрично на Х ↔ (х R y _^ x≠y →yRx).

опр.

Граф антисимметричного отношения обладает особенностью: если две вершины графа соединены стрелкой, то эта стрелка только одна. Справедливо и обратное утверждение: граф, вершины которого со­единены только одной стрелкой, есть граф антисимметричного отношения.

Кроме отношения «длиннее» на множестве отрезков свойством ан­тисимметричности, например, обладают:

— отношение «больше» для чисел (если х больше у, то у не может
быть больше х);

— отношение «больше на 2» для чисел (если х боль­ше у на 2, то у не может быть больше на 2 числа х),

Существуют отношения, не обладающие ни свой­ством симметричности, ни свойством антисиммет­ричности. Рассмотрим, например, отношение «быть сестрой» на множестве детей одной семьи. Пусть в семье трое детей: Катя, Маша и Толя. Тогда граф отношения «быть сестрой» будет таким, как на рисунке 100. Он показывает, что данное отношение не обладает ни свой­ством симметричности, ни свойством антисимметричности.

Определение. Отношение R на множестве X называется транзи­тивным, если выполняется условие; из того, что элемент х нахо­дится в отношении R с элементом у и элемент у находится в от­ношении R с элементом z, следует, что элемент х находится в от­ношении К с элементом z .

Используя символы, это определение можно записать в таком виде:

R транзитивно на X ↔ (х R y _^ yRz → xRz).

опр.

Граф транзитивного отношения с каждой парой стрелок, идущих от x к у и у к z, содержит стрелку, идущую от х к z. Справедливо и обратное утверждение.

Кроме отношения «длиннее» на множестве отрезков свойством транзитивности обладает отношение равенства: если отрезок х равен отрезку у и отрезок у равен отрезку z, то отрезок х равен отрезку z, Это свойство отражено и на графе отношения равенства (рис. 99)

Существуют отношения, которые свойством транзитивности не об­ладают. Таким отношением является, например, отношение перпенди­кулярности: если отрезок а перпендикулярен отрезку d, а отрезок d перпендикулярен отрезку b, то отрезки а и b не перпендикулярны!

Рассмотрим еще одно свойство отношений, которое называют свой­ством связанности, а отношение, обладающее им, называют связанным.

Определение. Отношение R на множестве X называется связан­ным, если для любых элементов х и у из множества X выполняется условие: из того, что х и у различны, следует, что либо х находит­ся в отношении R с элементом у, либо элемент у находится в от­ношении R с элементом х.

Используя символы, это определение можно записать в таком виде:

R связано на множестве X ↔ (х ≠ у => хRу v уRх).

опр.

Например, свойством связанности обладают отношения «больше» длянатуральных чисел: для любых различных чисел х и у можно ут­верждать, что либо х > у, либо у > х.

На графе связанного отношения любые две вершины соединены стрелкой. Справедливо и обратное утверждение.

Существуют отношения, которые свойством связанности не обла­дают. Таким отношением, например, является отношение делимости на множестве натуральных чисел: можно назвать такие числа х и у, что ни число х не является делителем числа у, ни число у не является делителем числа х.

Задача 1. Сформулировать свойства отноше­ния R, заданного при помощи графа (рис. 101).

Решение. Отношение R-антисимметрично, так как вершины графа соединяются только одной стрелкой.

Отношение R свойством рефлексивности не обла­дает, так как на графе есть вершины, в которых петли нет.

Задача 2. Сформулировать свойства отношения «больше в 2 раза», заданного на множестве натуральных чисел.

Данное отношение не обладает свойством рефлексивности, пото­му что ни про одно число нельзя сказать, что оно больше самого себя в 2 раза.

Заданное отношение не транзитивно, так как из того, что число x больше числа у на 2, а число у больше числа z на 2, следует, что число х не может быть больше числа z на 2.

Это отношение на множестве натуральных чисел свойством связан­ности не обладает, так как существуют пары таких чисел х и у, что ни число х не больше числа у в два раза, ни число у не больше х в 2 раза. Например, это числа 7 и 3, 5 и 8 и др.

Упражнения

1.Докажите, что отношение R, заданное при помощи графа (рис.102), рефлексивно, анти­симметрично и транзитивно.

2.Докажите, что отношение Т, заданное при помощи графа (рис.103), симметрично и тран­зитивно.

3.Сформулируйте условия, при которых от­ношение свойством рефлексивности не облада­ет, и докажите, что отношение Т (см. упр. 2) не рефлексивно.

4. Сформулируйте условия, при которых от­ношение не обладает свойством: а) симметричности; б) антисимметричности; в)транзитивно­сти; г) связанности.

5. Докажите, что отношение Р, граф которого изображен на рисунке 104, не обладает ни свойством симметричности, ни свойством антисимметричности, ни свойством транзитив­ности.

6.Какими свойствами обладает отношение, граф которого изображен на рисунке 105? Яв­ляется ли оно рефлексивным? Транзитивным?

7.Какие из следующих утверждений истинны:

а) Отношение «x больше у на 3» антисимметрично на множестве N, так как из того, что х больше у на 3, не следует, что у больше х на 3.

б) Отношение «x больше у на 3» антисимметрично, так как из того, что х больше у на 3, следует, что у не больше х на 3.

в) Отношение «х больше у на 3» антисим­метрично, так как из того, что х больше у на 3, следует, что у меньше х на 3.

8. На множестве отрезков задано отношение «короче». Верно ли, что оно антисимметрично
и транзитивно? Рефлексивно ли оно?

9. Какими свойствами обладают следующие отношения, заданные на множестве натуральных чисел:

а) «меньше»; б) «меньше на 2»; в) «меньше в 2 раза»?

10. На множестве X =<а, b, с>задано отношение R = <(а, b), (а, а), (b,b), (с, с), (b, а), (b, с), (с, b)>.Какими свойствами оно обладает?

11. На множестве Х= <2,4,6,8, 12>заданы отношения «больше» и «кратно». В чём их сходство и различие?

12.Установите, какое отношение рассматривается в задаче; какие приемы анализа задачи можно использовать:

а) Школьники сделали к карнавалу 15 шапочек для мальчиков, адля девочек в 2 раза больше. Сколько всего карнавальных шапочек они сделали?

б) Второклассники вырезали для елки 26 звездочек, это в 2 раза меньше, чем снежинок. Сколько всего звездочек и снежинок вырезали второклассники?

Дата добавления: 2016-05-11 ; просмотров: 7954 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Если отношение порядка обладает еще свойством связности, то говорят, что оно является отношением линейного порядка.

Например, отношение «меньше» на множестве натуральных чисел является отношением линейного порядка, так как обладает свойствами антисимметричности, транзитивности и связности.

Определение. Множество Х называется упорядоченным, если на нем задано отношение порядка.

Так, множество N натуральных чисел можно упорядочить, если задать на нем отношение «меньше».

Если отношение порядка, заданное на множестве Х, обладает свойством связности, то говорят, что оно линейно упорядочивает множество Х.

Например, множество натуральных чисел можно упорядочить и с помощью отношения «меньше», и помощью отношения «кратно» – оба они являются отношениями порядка. Но отношение «меньше», в отличие от отношения «кратно», обладает еще и свойством связности. Значит, отношение «меньше» упорядочивает множество натуральных чисел линейно.

Не следует думать, что все отношения делятся на отношения эквивалентности и отношения порядка. Существует огромное количество отношений, не являющихся ни отношениями эквивалентности, ни отношениями порядка.

ПРАКТИЧЕСКАЯ РАБОТА. ОТНОШЕНИЯ НА МНОЖЕСТВЕ

Цель. Выяснить на практике свойства, которыми могут обладать отношения: рефлексивности, симметричности, антисимметричности, транзитивности, связности. Раскрыть взаимосвязь между отношением эквивалентности на множестве и разбиением этого множества на классы.

Теоретическая часть

Вопросы к изучению

1. Понятие отношения между элементами одного множества.

2. Способы задания отношений.

3. Свойства бинарных отношений.

4. Отношение эквивалентности. Отношение порядка.

Основные понятия темы

Ø бинарное отношение на множестве;

Ø отношение эквивалентности;

Ø отношение порядка

Свойства отношений

Определения, замечания, выводы

Ø В зависимости от свойств отношения делятся на отношения эквивалентности, отношения порядка и отношения, которые не являются ни отношениями эквивалентности, ни отношениями порядка.

Ø Существует взаимосвязь между отношением эквивалентности на множестве Х и разбиением этого множества ни классы.

Практическая часть

1. Приведите примеры отношений, существующих между: а) натуральными числами; б) прямыми на плоскости; в) треугольниками; г) множествами.

2. На множестве Х= <0, 3, 6, 9, 12, 15, 18>задано отношение R. Перечислите пары чисел, связанных этим отношением и постройте его граф, если: а) R – « х больше у в 3 раза»; б) R – « х больше у на 3».

3. На множестве Х = <2, 4, 6, 8>рассматриваются отношения «х = у», «х у» и «х больше у на 2».Какое из приведенных ниже подмножеств множества Х ´ Х задает данные отношения: а) <(4,2),(6,2),(8, 4),(8,6),(2,2),(4,4),(6,6),(8,8)>; б) <(4,2),(6,4),(8, 6)>; в) <(2,2),(4,4),(6,6),(8,8)>.

4. Отношение « х ³ у» рассматривается на множестве Х. Каким будет его график на координатной плоскости, если: а) Х = <2,4,6,8>; б) Х – множество натуральных чисел; в) Х – множество действительных чисел?

5. На множестве отрезков задано отношение «короче». Верно ли, что оно антисимметрично и транзитивно? Рефлексивно ли оно?

7. На множестве отрезков задано отношение Р: «отрезок х длиннее отрезка у». Постройте граф этого отношения и задайте различными способами отношение, обратное данному.

6. Докажите, что отношение R, заданное при помощи графа рефлексивно, антисимметрично и транзитивно.

7. Докажите, что отношение Т, заданное при помощи графа симметрично и транзитивно.

8. Сформулируйте условия, при которых отношение свойством рефлексивности не обладает, и докажите, что отношение Т (см. упр. 7) не рефлексивно.

9. Докажите, что отношение Р, граф которого изображен на рисунке, не обладает ни свойством симметричности, ни свойством антисимметричности, ни свойством транзитивности.

10. Какими свойствами обладает отношение, граф которого изображен на рисунке? Является ли оно рефлексивным? Транзитивным?

11. Какие из следующих утверждений истинны: а) Отношение «х больше у на 3» антисимметрично на множестве N, так как из того, что х больше у на 3, не следует, что у больше х на 3; б) Отношение “х больше у на 3” антисимметрично, так как из того, что х больше у на 3, следует. Что у не больше х на 3; в) Отношение “х больше у на 3” антисимметрично, так как из того, что х больше у на 3, следует, что у меньше х на 3.

12. На множестве Х= задано отношение R = < (a,b), (a,a), (b,b), (c,c), (b,a), (b,c), (c,b)>. Какими свойствами оно обладает?

13. На множестве Х= <2, 4, 6, 8, 12>заданы отношения «больше» и «кратно». В чем их сходство и различие?

14. Установите, какое отношение рассматривается в задаче; какие приемы анализа задачи можно использовать:

а) Школьники сделали к карнавалу 15 шапочек для мальчиков, а для девочек в 2 раза больше. Сколько всего карнавальных шапочек они сделали?

б) Второклассники вырезали для елки 26 звездочек, это в 2 раза меньше. Чем снежинок. Сколько всего звездочек и снежинок вырезали второклассники?

15. Объясните, почему отношение равенства отрезков является отношением эквивалентности, а отношение «короче» не является.

16. Х – множество прямых плоскости. Какое из следующих отношений является отношением эквивалентности на этом множестве: а) «х параллельна у»; б) «х перпендикулярна у»; в) «х пересекает у»?

17. На множестве Х = <1,2,3,4,5,6,7,8,9,10>задано отношение «иметь один и тот же остаток при делении на 4». Является ли оно отношением эквивалентности?

18. Можно ли разбить множество Х = <7-3; 2 2 ; 5´2; 60: 6; 1+ 3; 0: 4; 0´10; 4:10-10)>на классы при помощи отношения «иметь равные значения»?

19. На множестве Х = <213, 37, 21, 87, 82>задано отношение Р – «иметь в записи одинаковые цифры». Является ли Р отношением эквивалентности?

20. На множестве целых чисел от 0 до 999 задано отношение К – «иметь в записи одно и то же число цифр». Покажите, что К – отношение эквивалентности. На сколько классов эквивалентности разбивается данное множество при помощи отношения К? Назовите наименьший и наибольший элементы каждого класса.

21. Сколько классов эквивалентности порождает на множестве натуральных чисел отношение «оканчиваться одной и той же цифрой». Назовите по одному представителю каждого класса.

22. Х – множество отрезков. Какие из следующих отношений являются отношениями порядка на этом множестве: а) «х равно у»; б) «х длиннее у»; в) «х длиннее у в 3 раза»?

23. Упорядочивают ли множество натуральных чисел отношения: а) «больше в 2 раза»; б) «больше на 2»; в) «непосредственно следовать за»; г) «х – делитель у»?

24. Отношение Т – «иметь одно и то же число делителей» задано на множестве Х = <1, 2, 4, 6, 7, 8, 10, 11>. Является ли Т отношением эквивалентности? Отношением порядка?

25. Выясните, какие из следующих высказываний истинны, а какие ложны; свой ответ обоснуйте:

а) Отношение «х кратно у» на множестве натуральных чисел рефлексивно и симметрично.

б) Отношение «х кратно у» на множестве натуральных чисел антисимметрично и транзитивно.

в) Отношение «х кратно у» на множестве натуральных чисел является отношением порядка.

26. Между множествами существуют отношения равенства, равномощности, «быть подмножеством». Какие из них являются отношениями эквивалентности, а какие отношениями порядка?

27. Решите задачи для младших школьников и укажите свойства отношений, которые были при этом использованы: а) Мальчик составил пирамидку из трех колечек: желтого, красного и зеленого. В каком порядке он расположил колечки, если желтое больше зеленого, а красное меньше зеленого? б) Четверо учащихся получили разные оценки за контрольную работу. Игорь получил оценку выше, чем Петр, Петр ниже, чем Максим, но выше, чем Кирилл. Кто получил самую низкую оценку?

1. Транзитивно ли отношение, граф которого

2. Показать, что отношение «иметь одинаковые остатки при делении на 3» – эквивалентность.

3. Доказать, что если отношение несимметрично, то оно не может порождать разбиение множества на классы.

4. Доказать, что если отношение нетранзитивно, то оно не может порождать разбиение множества на классы.

5. Множество натуральных чисел разбито на множество однозначных, двузначных, трехзначных и т.д. чисел. Сформулируйте отношение эквивалентности, которому подчинено данное разбиение.

Дата добавления: 2021-01-26 ; просмотров: 182 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Контрольно-оценочные средства по учебной дисциплине «Математика», 2 курс

Государственное бюджетное профессиональное образовательное учреждение города Москвы «Московское среднее специальное училище олимпийского резерва № 4 имени А.Я. Гомельского (техникум)»

Департамента спорта и туризма города Москвы

среднего профессионального образования

программы подготовки специалистов среднего звена

49.02.01 Физическая культура

для промежуточной аттестации в 3 семестре

Согласовано: Утверждаю:

ЦМК по специальности Зам. директора по УР

49.02.01 Физическая культура

Протокол № ____ «__» _________ 20___ г.

от «__» _________ 20___ г.

__________/ Н.Н. Никитина

Составитель : Боднарь Е. Г, преподаватель

Контрольно-оценочные средства (КОС) являются составной частью образовательной программы среднего профессионального образования по подготовке специалистов среднего звена 49.02.01 Физическая культура и предназначены для контроля и оценки образовательных достижений обучающихся, освоивших программу дисциплины «Математика».

КОС включают контрольные материалы для проведения промежуточной аттестации в форме зачета.

КОС разработаны на основании:

ФГОС СПО по специальности 49.02.01 Физическая культура ;

Рекомендаций по разработке контрольно-оценочных средств (КОС) ФИРО Минобрнауки РФ;

Методических рекомендаций по формированию фонда оценочных средств УМЦ ПО ДОгМ;

рабочей программы дисциплины.

2. Результаты освоения дисциплины а, подлежащие проверке

КОС для промежуточной аттестации направлены на проверку и оценивание результатов обучения, знаний и умений:

(освоенные умения, усвоенные знания)

Коды формируемых профессиональных и общих компетенций

Основные показатели оценки

№ заданий, включенных в КОС

• применять математические методы для решения профессиональных задач;

Точность формули-ровок определений, теорем, формул;

Правильность, пол-нота и обоснован-ность решения, последовательность рассуждений.

• решать комбинаторные задачи, находить вероятность событий;

• анализировать результаты измерения величин с допустимой погрешностью, представлять их графически;

• выполнять приближенные вычисления;

Нахождение числа размещений, перестановок,

Нахождение вероятности случайного события;

Выполнение приближенных вычислений;

Правильность, пол-нота и обоснован-ность решения, последовательность рассуждений.

• проводить элементарную статистическую обработку информации и результатов исследований;

Составление закона распределения случайной величины;

Вычисление числовых характеристик случайных величин;

Правильность, пол-нота и обоснован-ность решения, последовательность рассуждений

• понятие множества, отношения между множествами, операции над ними;

Осуществление операций над множествами,

Правильность, пол-нота и обоснован-ность решения, последовательность рассуждений.

• способы обоснования истинности высказываний;

Правильность, пол-нота и обоснован-ность решения, последовательность рассуждений;

-конъюнкции и дизъюнкции высказываний

и высказывательных форм;

-высказываний с кванторами;

-отрицания высказываний и высказывательных форм.

— отношение логического следования между предложениями;

— отношение равносильности между предложениями.

• основные комбинаторные конфигурации;

Использование комбинаторных конфигураций для решения задач;

Правильность, пол-нота и обоснован-ность решения, последовательность рассуждений.

• способы вычисления вероятности событий;

Вычисление вероятности различных событий;

Правильность, пол-нота и обоснован-ность решения, последовательность рассуждений.

• понятие положительной скалярной величины, процесс ее измерения;

• стандартные единицы величин и соотношения между ними;

• правила приближенных вычислений и нахождения процентного соотношения;

Анализ результатов измерения величин с допустимой погрешностью;

Выполнение приближенных вычислений;

Правильность, пол-нота и обоснован-ность решения, последовательность рассуждений.

• методы математической статистики.

Изложение методов математической статистики.

Проведение элементарной статистической обработки информации;

Правильность, пол-нота и обоснован-ность решения, последовательность рассуждений.

3. Распределение КОС по темам дисциплины математика

Контрольно-оценочные средства представляют собой перечень практических заданий.

Практические задания охватывают разделы, темы учебной дисциплины:

Содержание учебного материала

№ заданий (из Перечня)

Тема 1.1. Понятие множества и элемента множества.

Тема 1.2. Операции над множествами

Тема 1.3. Понятие соответствия

Тема 1.4. Отношения на множестве

Раздел 2. Математические утверждения и их структура. Тема 2.1 Элементы математической логики

Тема 2.2 Высказывания и высказывательные формы

Тема 2.3 Структура теоремы. Виды теорем

Тема 2.4 Математическое доказательство

Раздел 3. Элементы теории вероятностей и математической статистики

Тема 3.1 Основные понятия комбинаторики

Тема 3.3. Случайные величины

Тема 3.4. Математическое ожидание

Раздел 4 Скалярная величина

Тема 4.1 Понятие положительной скалярной величины

4.1. Практические задания (ПЗ):

2. Найдите пересечение множеств А и В, если:

3. М – множество однозначных чисел, Р – множество нечётных натуральных чисел.

а) Из каких чисел состоит пересечение данных множеств?

б) Содержатся ли в нём числа – 7 и 9?

4. А – множество точек окружности, B – множество точек прямой а.

а) Из скольких элементов может состоять пересечение данных множеств?

б) Может ли оно быть пустым?

5. Начертите два треугольника так, чтобы их пересечением:

6. Используя координатную прямую, найдите пересечение множеств решений неравенств, в которых переменная х – действительное число:

7. Найдите объединение множеств А и В, если:

8. Среди следующих выражений найдите такие, которые представляют собой равные множества:

9. Найдите разность множеств А и В, если:

10. На множестве натуральных чисел рассматривается свойство «быть кратным 7».

Сколько классов разбиения множества N оно определяет?

Назовите по два элемента из каждого класса.

11. Из множества четырёхугольников выделили подмножество фигур с попарно параллельными сторонами.

На какие классы разбивается множество четырехугольников с помощью свойства «иметь попарно параллельные стороны»?

Начертите по два четырёхугольника из каждого класса.

12. Из 32 школьников 12 занимаются в волейбольной секции, 15 – в баскетбольной, 8 человек занимаются и в той и в другой секции.

Сколько школьников не занимаются ни в волейбольной, ни в баскетбольной секции?

13. В делегации 6 человек, знающих французский или немецкий язык. Трое из них говорят только на французском, двое – только на немецком.

Сколько человек говорят на двух языках – французском и немецком?

14. Из 100 студентов английский язык изучают 28 человек, немецкий – 30 человек, французский – 42 человека, английский и немецкий – 8 человек, английский и французский – 10, немецкий и французский – 5. Все три языка изучают три студента.

Сколько студентов изучают только один язык?

Сколько студентов не изучают ни одного языка?

15. В школе 70 учеников. Из них 27 ходят в драмкружок, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов. 3 спортсмена посещают и драмкружок, и хор.

Сколько ребят никуда не ходят?

Сколько ребят занимаются только спортом?

16. Между множеством Х – углов треугольника АВС и множеством Y – его сторон задано соответствие Т – « угол х лежит против стороны у ». Задайте соответствие Т-1, обратное соответствию Т, при помощи:

а) предложения с двумя переменными;

17. Задайте при помощи графа соответствия между множествами

так, чтобы одно из них было взаимно однозначным.

18. Докажите, что множество А счётно, если:

19. Докажите, что отношение R, заданное при помощи графа рефлексивно, антисимметрично и транзитивно.

21. Докажите, что отношение Р, граф которого изображён на рисунке, не обладает ни свойством симметричности, ни свойством антисимметричности, ни свойством транзитивности.

22. Найдите А ∪ В, А ∩ В, А \ В, если:

23. Из множества К = <0, 2, 6, 8, 9, 12, 15>выделили два подмножества:

Произошло ли разбиение множества К на классы? Почему?

24. На множестве Х= <0, 3, 6, 9, 12, 15, 18>задано отношение R. Перечислите пары чисел, связанных этим отношением и постройте его граф, если:

а) R есть « х больше у в 3 раза »;

б) R есть « х больше у на 3 ».

25. Даны два множества А = <4, 6, 8>и В =<3, 7>.

Найдите множества А × В и В × А.

Можно ли установить взаимно однозначное соответствие между ними?

26. Проверьте справедливость равенства

(А \ В) × С = (А × С) \ (В × С)

для множеств А = <3, 5, 7>, В = <5, 7>, С = <1, 4>.

27. На множестве Х = <12, 13, 14, 15, 16, 17, 18, 19, 20, 21>задано отношение « иметь один и тот же остаток от деления на 4 ».

Показать, что данное отношение есть отношение эквивалентности, записать все классы эквивалентности, на которые разбивается множество Х, построить граф этого отношения.

28. Изобразите на координатной плоскости множества истинности следующих предложений при условии, что х ∈ R, у ∈ R:

29. Решите следующие системы неравенств и объясните, что представляет собой любая система неравенств и множество её решений с точки зрения логики:

Использовалось ли вами понятие дизъюнкции высказывательных форм?

31. Вместо многоточия вставьте «и» либо «или»:

а) х ∈ А ∩ В тогда и только тогда, когда х ∈ А … х ∈ В;

б) х ∈ А ∪ В тогда и только тогда, когда х ∈ А … х ∈ В.

32. Пусть А – множество ромбов, В – множество прямоугольников.

Как называется четырёхугольник, являющийся одновременно ромбом и прямоугольником?

Как можно выразить множество К таких четырёхугольников через множества А и В?

33. Установите, какие из нижеприведенных высказываний истинны.

1) Во всяком четырёхугольнике диагонали равны;

2) Существуют числовые выражения, значения которых нельзя найти;

3) При делении на 5 некоторых натуральных чисел в остатке получается 7;

4) Любое однозначное число является решением неравенства х + 2 > 1.

34. Установите, какие из нижеприведенных высказываний истинны.

1) Существуют уравнения, множество решений которых пусто;

2) Всякое целое число является натуральным;

3) Сумма любых двух чётных чисел есть число чётное;

4) Хотя бы одно натуральное число является решением уравнения 7: х =2.

35. Переформулируйте данные предложения так, чтобы они не содержали слов «неверно, что», но имели тот же смысл:

а) Неверно, что число 9 – чётное или простое;

б) Неверно, что треугольник АВС – равнобедренный и прямоугольный;

в) Неверно, что каждый четырёхугольник является прямоугольником;

г) Неверно, что хотя бы в одном прямоугольнике диагонали взаимно перпендикулярны.

36. Сформулируйте предложения, которые начинаются словами «неверно, что» и имеют тот же смысл, что и данные:

а) Прямые АВ и СД не параллельны и не пересекаются;

б) Стороны четырёхугольника АВСД не параллельны или не равны;

в) Существуют уравнения, не имеющие действительных корней;

г) Все прямоугольники не имеют равных смежных сторон.

37. Установите, находятся ли данные пары предложений в отношении следования:

38. Равносильны ли следующие предложения А(х) и В(х), если:

39. Какие из нижеприведенных высказываний истинные:

а) Для того, чтобы число делилось на 3, достаточно, чтобы оно делилось на 6;

б) Для того чтобы число делилось на 3, необходимо, чтобы оно делилось на 6;

в) Для того чтобы число делилось на 100, необходимо и достаточно, чтобы оно делилось на 10;

г) Для того чтобы число делилось на 10, необходимо и достаточно, чтобы оно делилось на 2 и на 5.

40. Вместо многоточия вставьте слова «необходимо» либо «достаточно», либо «необходимо и достаточно», чтобы данные предложения были истинными:

а) Для того чтобы сумма двух натуральных чисел делилась на 2, …, чтобы каждое слагаемое делилось на 2;

41. Вставьте слова «и» либо «или» так, чтобы следующие высказывания были истинными:

а) а × в = 0 ⇔ а = 0 … в = 0;

б) а × в ≠ 0 ⇔ а ≠ 0 … в ≠ 0;

в) х ∈ А ∩ В ⇔ х ∈ А … х ∈ В;

г) х А ∩ В ⇔ х А … х В.

42. Докажите методом математической индукции, что

а) 1 + 3 + 5 + … + (2n – 1) = n2;

б) 1 + 3 + 6 + … + (n (n+1))/2 = (n (n+1)(n+2))/6 ;

в) 12 + 22 + 32 + … + n2 = (n (n+1)(2n+1))/6 ;

а. б. в. г.

44. Решите следующие задачи, построив дерево возможных вариантов:

а) У продавца имеется три варианта мороженого: клубничное, сливочное и ореховое. Наташа и Катя решили купить по одной порции. Сколько существует вариантов такой покупки?

б) Туристическая фирма планирует посещение туристами в Италии трёх городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута?

45. 10 выпускников пришли в кафе отпраздновать окончание школы, но не могли решить, как сесть, то есть в каком порядке. На выручку пришёл официант, который предложил сесть сегодня, как придётся, а на другой день сесть по-другому и так до тех пор, пока не наступит такой день, когда они сядут как в первый раз. Тогда их официант обещал угостить бесплатным обедом.

Как вы думаете, долго ли друзьям ждать бесплатного обеда?

46. Сколько трёхзначных чисел можно составить из цифр 1, 3, 5 и 7, используя в записи числа каждую из них не более одного раза?

47. Студенты 1 курса изучают 10 предметов. Сколькими способами можно составить расписание на один день, чтобы в нём было 4 различных предмета?

48. Сколько имеется слов длиной 3 с неповторяющимися буквами в алфавите из 6 букв?

49. В магазине «Филателия» продаётся 8 различных наборов марок, посвящённых спортивной тематике. Сколькими способами можно выбрать из них 3 набора?

50. Из 18-ти студентов группы надо выбрать двух дежурных. Сколькими способами можно сделать этот выбор?

51. Из шести врачей поликлиники двух необходимо отправить на курсы повышения квалификации. Сколькими способами это можно сделать?

52. Сколько различных двухзначных чисел можно составить, используя цифры 1, 2, 3, 4 при условии, что ни одна цифра не повторяется?

53. В группе 7 студентов успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в олимпиаде по предмету?

54. Сколько различных трёхзначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что ни одна цифра не повторяется?

55. В ящике находится 15 деталей. Сколькими способами можно взять 4 детали?

56. Сколькими способами из колоды в 36 карт можно выбрать 3 карты?

57. В шахматном турнире участвует k человек и каждый с каждым играет по одной партии. Сколько всего партий сыграно в турнире?

58. Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно выбрать двух человек одного пола?

59. Алексей занимается спортом, причём 4 дня в неделю – лёгкой атлетикой, 2 дня – силовыми упражнениями и 1 день отдыхает. Сколькими способами он может составить себе расписание занятий на неделю?

60. В студенческой столовой продают сосиски в тесте, ватрушки и пончики. Сколькими способами можно приобрести пять пирожков?

61. В кошельке находится достаточно большое количество рублей, 2-, 5- и 10-рублёвых монет. Сколькими способами можно извлечь три монеты из кошелька?

62. Согласно государственному стандарту, автомобильный номерной знак состоит из 3 цифр и 3 букв. При этом недопустим номер с тремя нулями, а буквы выбираются из набора А, В, Е, К, М, Н, О, Р, С, Т, У, Х (используются только те буквы кириллицы, написание которых совпадает с латинскими буквами).

63. Конференция длится три дня. В первый и второй день выступают по 15 докладчиков, в третий день – 20. Какова вероятность того, что доклад профессора М. выпадет на третий день, если порядок докладов определяется жеребьевкой?

64. В жеребьевке участвуют 5 немцев, 8 французов и 3 эстонца. Какова вероятность того, что первым (/вторым/седьмым/последним – не важно) будет выступать француз.

65. Когда подбрасываем монету, какова вероятность выпадения решки?

66. А если подбрасываем монету два раза? Какова вероятность того, что оба раза выпадет орел?

67. Бросаем игральную кость. Какова вероятность, что выпадет четное число?

68. Бросаем две игральные кости. Какова вероятность, что в сумме выпадет 10? (округлить до сотых)

69. В лотерее выпущено 100 билетов. Разыгрывался один выигрыш в 50 у.е. и десять выигрышей по 10 у.е. Найти закон распределения величины X – стоимости возможного выигрыша.

70. Вероятность того, что покупатель ознакомился заранее с рекламой товара равна 0,6 (р=0,6). Осуществляется выборочный контроль качества рекламы путем опроса покупателей до первого, изучившего рекламу заранее. Составить ряд распределения количества опрошенных покупателей.

71. Компьютер состоит из трех независимо работающих элементов: системного блока, монитора и клавиатуры. При однократном резком повышении напряжения вероятность отказа каждого элемента равна 0,1. Исходя из распределения Бернулли составить закон распределения числа отказавших элементов при скачке напряжения в сети.

73. При стрельбе до первого попадания с вероятностью попадания p = 0,6 при выстреле надо найти вероятность того, что попадание произойдет при третьем выстреле.

74. Пусть задан закон распределения случайной величины X:

Найти математическое ожидание.

75. Найти дисперсию случайной величины X со следующим законом распределения:

76. Пусть случайная величина задается распределением:

Найти её числовые характеристики.

77. Найти числовые характеристики дискретной случайной величины X, заданной законом распределения:

79. Производятся 4 независимых выстрела в одинаковых условиях, причем вероятность попадания в цель равна 0,25. Найти вероятности ни одного попадания, одного, двух, трех и четырех попаданий; вероятность того, что число попаданий – не менее одного и не более трех.

80. Передается 3 сообщения по каналу связи. Каждое сообщение с вероятностью 0,3 независимо от других искажается. Составить закон распределения числа искаженных сообщений. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение и наивероятнейшее число искаженных сигналов.

81. Найдите относительную погрешность и выразите ее в процентах. В приближенном значении x определите верные и сомнительные цифры:

5. Описание процедуры проведения промежуточной аттестации.

Зачет проводится за счет часов, отведенных на учебную дисциплину, в учебное время по заданиям, согласованным на ЦМК и утвержденным заместителем директора по УР.

Время на и выполнение:

оформление и сдача 5 мин.;

№ 3. а) Множество однозначных нечётных натуральных чисел.

Источник