Докажите что отношение r заданное с помощью графа рефлексивно антисимметрично и транзитивно
Если отношение порядка обладает еще свойством связности, то говорят, что оно является отношением линейного порядка.
Например, отношение «меньше» на множестве натуральных чисел является отношением линейного порядка, так как обладает свойствами антисимметричности, транзитивности и связности.
Определение. Множество Х называется упорядоченным, если на нем задано отношение порядка.
Так, множество N натуральных чисел можно упорядочить, если задать на нем отношение «меньше».
Если отношение порядка, заданное на множестве Х, обладает свойством связности, то говорят, что оно линейно упорядочивает множество Х.
Например, множество натуральных чисел можно упорядочить и с помощью отношения «меньше», и помощью отношения «кратно» – оба они являются отношениями порядка. Но отношение «меньше», в отличие от отношения «кратно», обладает еще и свойством связности. Значит, отношение «меньше» упорядочивает множество натуральных чисел линейно.
Не следует думать, что все отношения делятся на отношения эквивалентности и отношения порядка. Существует огромное количество отношений, не являющихся ни отношениями эквивалентности, ни отношениями порядка.
ПРАКТИЧЕСКАЯ РАБОТА. ОТНОШЕНИЯ НА МНОЖЕСТВЕ
Цель. Выяснить на практике свойства, которыми могут обладать отношения: рефлексивности, симметричности, антисимметричности, транзитивности, связности. Раскрыть взаимосвязь между отношением эквивалентности на множестве и разбиением этого множества на классы.
Теоретическая часть
Вопросы к изучению
1. Понятие отношения между элементами одного множества.
2. Способы задания отношений.
3. Свойства бинарных отношений.
4. Отношение эквивалентности. Отношение порядка.
Основные понятия темы
Ø бинарное отношение на множестве;
Ø отношение эквивалентности;
Ø отношение порядка
Свойства отношений
Определения, замечания, выводы
Ø В зависимости от свойств отношения делятся на отношения эквивалентности, отношения порядка и отношения, которые не являются ни отношениями эквивалентности, ни отношениями порядка.
Ø Существует взаимосвязь между отношением эквивалентности на множестве Х и разбиением этого множества ни классы.
Практическая часть
1. Приведите примеры отношений, существующих между: а) натуральными числами; б) прямыми на плоскости; в) треугольниками; г) множествами.
2. На множестве Х= <0, 3, 6, 9, 12, 15, 18>задано отношение R. Перечислите пары чисел, связанных этим отношением и постройте его граф, если: а) R – « х больше у в 3 раза»; б) R – « х больше у на 3».
3. На множестве Х = <2, 4, 6, 8>рассматриваются отношения «х = у», «х 
у» и «х больше у на 2».Какое из приведенных ниже подмножеств множества Х ´ Х задает данные отношения: а) <(4,2),(6,2),(8, 4),(8,6),(2,2),(4,4),(6,6),(8,8)>; б) <(4,2),(6,4),(8, 6)>; в) <(2,2),(4,4),(6,6),(8,8)>.
4. Отношение « х ³ у» рассматривается на множестве Х. Каким будет его график на координатной плоскости, если: а) Х = <2,4,6,8>; б) Х – множество натуральных чисел; в) Х – множество действительных чисел?
5. На множестве отрезков задано отношение «короче». Верно ли, что оно антисимметрично и транзитивно? Рефлексивно ли оно?
7. На множестве отрезков задано отношение Р: «отрезок х длиннее отрезка у». Постройте граф этого отношения и задайте различными способами отношение, обратное данному.
6. Докажите, что отношение R, заданное при помощи графа рефлексивно, антисимметрично и транзитивно.
7. Докажите, что отношение Т, заданное при помощи графа симметрично и транзитивно.
8. Сформулируйте условия, при которых отношение свойством рефлексивности не обладает, и докажите, что отношение Т (см. упр. 7) не рефлексивно.
9. Докажите, что отношение Р, граф которого изображен на рисунке, не обладает ни свойством симметричности, ни свойством антисимметричности, ни свойством транзитивности.
10. Какими свойствами обладает отношение, граф которого изображен на рисунке? Является ли оно рефлексивным? Транзитивным?
11. Какие из следующих утверждений истинны: а) Отношение «х больше у на 3» антисимметрично на множестве N, так как из того, что х больше у на 3, не следует, что у больше х на 3; б) Отношение “х больше у на 3” антисимметрично, так как из того, что х больше у на 3, следует. Что у не больше х на 3; в) Отношение “х больше у на 3” антисимметрично, так как из того, что х больше у на 3, следует, что у меньше х на 3.
12. На множестве Х=
13. На множестве Х= <2, 4, 6, 8, 12>заданы отношения «больше» и «кратно». В чем их сходство и различие?
14. Установите, какое отношение рассматривается в задаче; какие приемы анализа задачи можно использовать:
а) Школьники сделали к карнавалу 15 шапочек для мальчиков, а для девочек в 2 раза больше. Сколько всего карнавальных шапочек они сделали?
б) Второклассники вырезали для елки 26 звездочек, это в 2 раза меньше. Чем снежинок. Сколько всего звездочек и снежинок вырезали второклассники?
15. Объясните, почему отношение равенства отрезков является отношением эквивалентности, а отношение «короче» не является.
16. Х – множество прямых плоскости. Какое из следующих отношений является отношением эквивалентности на этом множестве: а) «х параллельна у»; б) «х перпендикулярна у»; в) «х пересекает у»?
17. На множестве Х = <1,2,3,4,5,6,7,8,9,10>задано отношение «иметь один и тот же остаток при делении на 4». Является ли оно отношением эквивалентности?
18. Можно ли разбить множество Х = <7-3; 2 2 ; 5´2; 60: 6; 1+ 3; 0: 4; 0´10; 4:10-10)>на классы при помощи отношения «иметь равные значения»?
19. На множестве Х = <213, 37, 21, 87, 82>задано отношение Р – «иметь в записи одинаковые цифры». Является ли Р отношением эквивалентности?
20. На множестве целых чисел от 0 до 999 задано отношение К – «иметь в записи одно и то же число цифр». Покажите, что К – отношение эквивалентности. На сколько классов эквивалентности разбивается данное множество при помощи отношения К? Назовите наименьший и наибольший элементы каждого класса.
21. Сколько классов эквивалентности порождает на множестве натуральных чисел отношение «оканчиваться одной и той же цифрой». Назовите по одному представителю каждого класса.
22. Х – множество отрезков. Какие из следующих отношений являются отношениями порядка на этом множестве: а) «х равно у»; б) «х длиннее у»; в) «х длиннее у в 3 раза»?
23. Упорядочивают ли множество натуральных чисел отношения: а) «больше в 2 раза»; б) «больше на 2»; в) «непосредственно следовать за»; г) «х – делитель у»?
24. Отношение Т – «иметь одно и то же число делителей» задано на множестве Х = <1, 2, 4, 6, 7, 8, 10, 11>. Является ли Т отношением эквивалентности? Отношением порядка?
25. Выясните, какие из следующих высказываний истинны, а какие ложны; свой ответ обоснуйте:
а) Отношение «х кратно у» на множестве натуральных чисел рефлексивно и симметрично.
б) Отношение «х кратно у» на множестве натуральных чисел антисимметрично и транзитивно.
в) Отношение «х кратно у» на множестве натуральных чисел является отношением порядка.
26. Между множествами существуют отношения равенства, равномощности, «быть подмножеством». Какие из них являются отношениями эквивалентности, а какие отношениями порядка?
27. Решите задачи для младших школьников и укажите свойства отношений, которые были при этом использованы: а) Мальчик составил пирамидку из трех колечек: желтого, красного и зеленого. В каком порядке он расположил колечки, если желтое больше зеленого, а красное меньше зеленого? б) Четверо учащихся получили разные оценки за контрольную работу. Игорь получил оценку выше, чем Петр, Петр ниже, чем Максим, но выше, чем Кирилл. Кто получил самую низкую оценку?
1. Транзитивно ли отношение, граф которого
2. Показать, что отношение «иметь одинаковые остатки при делении на 3» – эквивалентность.
3. Доказать, что если отношение несимметрично, то оно не может порождать разбиение множества на классы.
4. Доказать, что если отношение нетранзитивно, то оно не может порождать разбиение множества на классы.
5. Множество натуральных чисел разбито на множество однозначных, двузначных, трехзначных и т.д. чисел. Сформулируйте отношение эквивалентности, которому подчинено данное разбиение.
Дата добавления: 2021-01-26 ; просмотров: 183 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Лекция 21. Свойства отношений
1. Свойство рефлексивености
2. Свойство симметричности
3. Свойство транзитивности
Свойства отношений
Мы установили, что бинарное отношение на множестве X представляет собой множество упорядоченных пар элементов, принадлежащих декартову произведению X х Х. Это математическая сущность всякого отношения. Но, как и любые другие понятия, отношения обладают свойствами. Их удалось выделить, изучая различные конкретные отношения. Свойств достаточно много, в нашем курсе мы будем изучать только некоторые.
Определение. Отношение R на множестве X называется рефлексивным, если о каждом элементе множества X можно сказать, что он находится в отношении R с самим собой.
Используя символы, это отношение можно записать в таком виде:
R рефлексивно на Х ↔ х R х для любого х € X.
Если отношение R рефлексивно на множестве X, то в каждой вершине графа данного отношения имеется петля. Справедливо и обратное утверждение: граф, каждая вершина которого имеет петлю, задает отношения, обладающие свойством рефлексивности.
Примеры рефлексивных отношений:
— отношение «кратно» на множестве натуральных чисел (каждое натуральное число кратно самому себе);
— отношение подобия треугольников (каждый треугольник подобен самому себе).
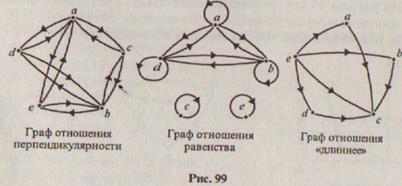
Существуют отношения, которые свойством рефлексивности не обладают. Таким, например, является отношение перпендикулярности на множестве отрезков: нет ни одного отрезка, о котором можно сказать, что он перпендикулярен самому себе. Поэтому на графе отношения перпендикулярности (рис. 99) нет ни одной петли. Не обладает свойством рефлексивности и отношение «длиннее» для отрезков.
Обратим теперь внимание на графы отношений перпендикулярности и равенства отрезков. Они «похожи» тем, что если есть одна стрелка, соединяющая пару элементов, то обязательно есть и другая, соединяющая те же элементы, но идущая в противоположном направлении. Эта особенность графа отражает те свойства, которыми обладают отношения параллельности и равенства отрезков:
— если один отрезок перпендикулярен другому отрезку, то этот «другой» перпендикулярен первому;
— если один отрезок равен другому отрезку, то этот «другой» равен первому.
Про отношения перпендикулярности и равенства отрезков говорят, что они обладают свойством симметричности или просто симметричны.
Определение. Отношение R на множестве X называется симметричным, если выполняется условие: из того, что элемент х находится в отношении R с элементом у, следует, что и элементу находится в отношении R с элементом х.
Используя символы, это отношение можно записать в таком виде:
R симметрично на Х ↔ (х R y →yRx).
опр.
Граф симметричного отношения обладает особенностью: вместе с каждой стрелкой, идущей от х к у, граф содержит и стрелку, идущую от у к x. Справедливо и обратноеутверждение. Граф, содержащий вместе с каждой стрелкой, идущей от x к у, и стрелку, идущую от у к x, является графом симметричного отношения.
В дополнение к рассмотренным двум примерам симметричных отношений присоединим еще такие:
-отношениепараллельности на множестве прямых (если прямая x параллельна прямой у, то и прямая у параллельна прямой х)
-отношение подобия треугольников (если треугольник F подобен треугольнику Р, то треугольник Р подобен треугольнику F).
Существуют отношения, которые свойством симметричности не обладают. Таким, например, является отношение «длиннее» на множестве отрезков. Действительно, если отрезок x длиннее отрезка у, то отрезок у не может быть длиннее отрезка х. Про отношения «длиннее» говорят, что оно обладает свойством антисимметричности или просто антисимметрично.
Определение. Отношение R на множестве X называется антисимметричным, если для различных элементов х и у из множества X выполнено условие: из того, что х находится в отношении R с элементом у, следует, что элемент у в отношении R с элементом х не находится.
Используя символы, это определение можно записать в таком виде:
R симметрично на Х ↔ (х R y ^ x≠y →yRx).
опр.
Граф антисимметричного отношения обладает особенностью: если две вершины графа соединены стрелкой, то эта стрелка только одна. Справедливо и обратное утверждение: граф, вершины которого соединены только одной стрелкой, есть граф антисимметричного отношения.
Кроме отношения «длиннее» на множестве отрезков свойством антисимметричности, например, обладают:
— отношение «больше» для чисел (если х больше у, то у не может
быть больше х);
— отношение «больше на 2» для чисел (если х больше у на 2, то у не может быть больше на 2 числа х),
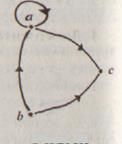
Существуют отношения, не обладающие ни свойством симметричности, ни свойством антисимметричности. Рассмотрим, например, отношение «быть сестрой» на множестве детей одной семьи. Пусть в семье трое детей: Катя, Маша и Толя. Тогда граф отношения «быть сестрой» будет таким, как на рисунке 100. Он показывает, что данное отношение не обладает ни свойством симметричности, ни свойством антисимметричности.
Определение. Отношение R на множестве X называется транзитивным, если выполняется условие; из того, что элемент х находится в отношении R с элементом у и элемент у находится в отношении R с элементом z, следует, что элемент х находится в отношении К с элементом z .
Используя символы, это определение можно записать в таком виде:
R транзитивно на X ↔ (х R y ^ yRz → xRz).
опр.
Граф транзитивного отношения с каждой парой стрелок, идущих от x к у и у к z, содержит стрелку, идущую от х к z. Справедливо и обратное утверждение.
Кроме отношения «длиннее» на множестве отрезков свойством транзитивности обладает отношение равенства: если отрезок х равен отрезку у и отрезок у равен отрезку z, то отрезок х равен отрезку z, Это свойство отражено и на графе отношения равенства (рис. 99)
Существуют отношения, которые свойством транзитивности не обладают. Таким отношением является, например, отношение перпендикулярности: если отрезок а перпендикулярен отрезку d, а отрезок d перпендикулярен отрезку b, то отрезки а и b не перпендикулярны!
Рассмотрим еще одно свойство отношений, которое называют свойством связанности, а отношение, обладающее им, называют связанным.
Определение. Отношение R на множестве X называется связанным, если для любых элементов х и у из множества X выполняется условие: из того, что х и у различны, следует, что либо х находится в отношении R с элементом у, либо элемент у находится в отношении R с элементом х.
Используя символы, это определение можно записать в таком виде:
R связано на множестве X ↔ (х ≠ у => хRу v уRх).
опр.
Например, свойством связанности обладают отношения «больше» длянатуральных чисел: для любых различных чисел х и у можно утверждать, что либо х > у, либо у > х.
На графе связанного отношения любые две вершины соединены стрелкой. Справедливо и обратное утверждение.
Существуют отношения, которые свойством связанности не обладают. Таким отношением, например, является отношение делимости на множестве натуральных чисел: можно назвать такие числа х и у, что ни число х не является делителем числа у, ни число у не является делителем числа х.
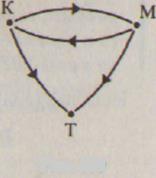
Задача 1. Сформулировать свойства отношения R, заданного при помощи графа (рис. 101).
Решение. Отношение R-антисимметрично, так как вершины графа соединяются только одной стрелкой.
Отношение R свойством рефлексивности не обладает, так как на графе есть вершины, в которых петли нет.
Задача 2. Сформулировать свойства отношения «больше в 2 раза», заданного на множестве натуральных чисел.
Данное отношение не обладает свойством рефлексивности, потому что ни про одно число нельзя сказать, что оно больше самого себя в 2 раза.
Заданное отношение не транзитивно, так как из того, что число x больше числа у на 2, а число у больше числа z на 2, следует, что число х не может быть больше числа z на 2.
Это отношение на множестве натуральных чисел свойством связанности не обладает, так как существуют пары таких чисел х и у, что ни число х не больше числа у в два раза, ни число у не больше х в 2 раза. Например, это числа 7 и 3, 5 и 8 и др.
Упражнения
1.Докажите, что отношение R, заданное при помощи графа (рис.102), рефлексивно, антисимметрично и транзитивно.
2.Докажите, что отношение Т, заданное при помощи графа (рис.103), симметрично и транзитивно.
3.Сформулируйте условия, при которых отношение свойством рефлексивности не обладает, и докажите, что отношение Т (см. упр. 2) не рефлексивно.
4. 
Сформулируйте условия, при которых отношение не обладает свойством: а) симметричности; б) антисимметричности; в)транзитивности; г) связанности.
5. 
Докажите, что отношение Р, граф которого изображен на рисунке 104, не обладает ни свойством симметричности, ни свойством антисимметричности, ни свойством транзитивности.
6.Какими свойствами обладает отношение, граф которого изображен на рисунке 105? Является ли оно рефлексивным? Транзитивным?
7.Какие из следующих утверждений истинны:
а) Отношение «x больше у на 3» антисимметрично на множестве N, так как из того, что х больше у на 3, не следует, что у больше х на 3.
б) Отношение «x больше у на 3» антисимметрично, так как из того, что х больше у на 3, следует, что у не больше х на 3.
в) Отношение «х больше у на 3» антисимметрично, так как из того, что х больше у на 3, следует, что у меньше х на 3.
8. На множестве отрезков задано отношение «короче». Верно ли, что оно антисимметрично
и транзитивно? Рефлексивно ли оно?
9. Какими свойствами обладают следующие отношения, заданные на множестве натуральных чисел:
а) «меньше»; б) «меньше на 2»; в) «меньше в 2 раза»?
10. На множестве X =<а, b, с>задано отношение R = <(а, b), (а, а), (b,b), (с, с), (b, а), (b, с), (с, b)>.Какими свойствами оно обладает?
11. На множестве Х= <2,4,6,8, 12>заданы отношения «больше» и «кратно». В чём их сходство и различие?
12.Установите, какое отношение рассматривается в задаче; какие приемы анализа задачи можно использовать:
а) Школьники сделали к карнавалу 15 шапочек для мальчиков, адля девочек в 2 раза больше. Сколько всего карнавальных шапочек они сделали?
б) Второклассники вырезали для елки 26 звездочек, это в 2 раза меньше, чем снежинок. Сколько всего звездочек и снежинок вырезали второклассники?
Дата добавления: 2016-05-11 ; просмотров: 7955 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Курс лекций по математике. Учебнометодический комплекс по дисциплине Конспект лекций (на правах рукописи) Абакан
Граф транзитивного отношения с каждой парой стрелок, идущих от x к у и у к z, содержит стрелку, идущую от х кz. Справедливо и обратное утверждение.
Кроме отношения «длиннее» на множестве отрезков свойством транзитивности обладает отношение равенства: если отрезок х равен отрезку у и отрезок у равен отрезку z, то отрезок х равен отрезку z, Это свойство отражено и на графе отношения равенства (рис. 99)
Существуют отношения, которые свойством транзитивности не обладают. Таким отношением является, например, отношение перпендикулярности: если отрезок а перпендикулярен отрезку d, а отрезок dперпендикулярен отрезку b, то отрезки а и bне перпендикулярны!
Рассмотрим еще одно свойство отношений, которое называют свойством связанности, а отношение, обладающее им, называют связанным.
Определение. Отношение R на множестве X называется связанным, если для любых элементов х и у из множества X выполняется условие: из того, что х и у различны, следует, что либо х находится в отношении R с элементом у, либо элемент у находится в отношении R с элементом х.
Используя символы, это определение можно записать в таком виде:
Например, свойством связанности обладают отношения «больше» для натуральных чисел: для любых различных чисел х и у можно утверждать, что либо х > у, либо у > х.
На графе связанного отношения любые две вершины соединены стрелкой. Справедливо и обратное утверждение.
Существуют отношения, которые свойством связанности не обладают. Таким отношением, например, является отношение делимости на множестве натуральных чисел: можно назвать такие числа х и у, что ни число х не является делителем числа у, ни число у не является делителем числа х.
Задача 1. Сформулировать свойства отношения R, заданного при помощи графа (рис. 101).
Решение. Отношение R-антисимметрично, так как вершины графа соединяются только одной стрелкой.
Отношение R — транзитивно, так как с парой стрелок, идущих от bк а и от а к с, на графе есть стрелка, идущая от bк с.
Отношение R — связанно, так как любые две вершины соединены стрелкой.
Отношение R свойством рефлексивности не обладает, так как на графе есть вершины, в которых петли нет.
Задача 2. Сформулировать свойства отношения «больше в 2 раза», заданного на множестве натуральных чисел.
Данное отношение не обладает свойством рефлексивности, потому что ни про одно число нельзя сказать, что оно больше самого себя в 2 раза.
Заданное отношение не транзитивно, так как из того, что число x больше числа у на 2, а число у больше числа zна 2, следует, что число х не может быть больше числа zна 2.
Э
то отношение на множестве натуральных чисел свойством связанности не обладает, так как существуют пары таких чисел х и у, что ни число х не больше числа у в два раза, ни число у не больше х в 2 раза. Например, это числа 7 и 3, 5 и 8 и др.
б) Отношение «x больше у на 3» антисимметрично, так как из того, что х больше у на 3, следует, что у не больше х на 3.
в) Отношение «х больше у на 3» антисимметрично, так как из того, что х больше у на 3, следует, что у меньше х на 3.
8. На множестве отрезков задано отношение «короче». Верно ли, что оно антисимметрично
и транзитивно? Рефлексивно ли оно?
9. Какими свойствами обладают следующие отношения, заданные на множестве натуральных чисел:
а) «меньше»; б) «меньше на 2»; в) «меньше в 2 раза»?
11. На множестве Х= <2,4,6,8, 12>заданы отношения «больше» и «кратно». В чём их сходство и различие?
12. Установите, какое отношение рассматривается в задаче; какие приемы анализа задачи можно использовать:
а) Школьники сделали к карнавалу 15 шапочек для мальчиков, адля девочек в 2 раза больше. Сколько всего карнавальных шапочек они сделали?
б) Второклассники вырезали для елки 26 звездочек, это в 2 раза меньше, чем снежинок. Сколько всего звездочек и снежинок вырезали второклассники?
Лекция 22. Отношения эквивалентности и порядка на множестве
1. Отношение эквивалентности. Связь отношения эквивалентности с разбиением множества на классы.
2. Отношение порядка. Строгое и нестрогое отношения порядка, отношение линейного порядка. Упорядоченность множеств.
3. Основные выводы
49. Отношения эквивалентности и порядка
Рассмотрим на множестве дробей X = <1>отношение равенства. Это отношение:
— рефлексивно, так как всякая дробь равна сама себе;
— симметрично, так как из того, что дробь m/n равна дроби p/q, следует, что дробь p/q равна дроби m/n;
— транзитивно, так как из того, что дробьm/n равна дроби p/qи дробь p/q равна дроби r/s, следует, что дробь m/n равна дроби r/s.
Про отношение равенства дробей говорят, что оно является отношением эквивалентности.
Определение. Отношение R на множестве X называется отношением эквивалентности, если оно одновременно обладает свойствами рефлексивности, симметричности и транзитивности.
Примерами отношений эквивалентности могут служить отношения равенства геометрических фигур, отношение параллельности прямых (при условии, что совпадающие прямые считаются параллельными).
П
очему в математике выделили этот вид отношений? Рассмотрим отношение равенства дробей, заданное на множестве X = <1>(Рис.106). Видим, что множество разбилось на три подмножества: <1>, <1>, <1>. Эти подмножества не пересекаются, а их объединение совпадает с множеством Х, т.е. имеем разбиение множества Xна классы. Это не случайно.
Вообще, если на множестве X задано отношение эквивалентности, то оно порождает разбиение этого множества на попарно непересекающиеся подмножества (классы эквивалентности).
Так, мы установили, что отношению равенства на множестве дробей <1>соответствует разбиение этого множества на классы эквивалентности, каждый из которых состоит из равных между собой дробей.
Верно и обратное утверждение: если какое-либо отношение, заданное на множестве X, порождает разбиение этого множества на классы, то оно является отношением эквивалентности.
Итак, имея отношение эквивалентности на некотором множестве, мы можем разбить это множество на классы. Но можно поступить и наоборот: сначала разбить множество на классы, а затем определить отношение эквивалентности, считая, что два элемента эквивалентны тогда и только тогда, когда они принадлежат одному классу рассматриваемого разбиения.
Принцип разбиения множества на классы при помощи некоторого отношения эквивалентности является важным принципом математики. Почему?
Во-вторых, поскольку в классе эквивалентности оказываются элементы, неразличимые с точки зрения некоторого отношения, то считают, что класс эквивалентности определяется любым своим представителем, т.е. произвольным элементом этого класса. Так, любой класс равных дробей можно задать, указав любую дробь, принадлежащую этому классу. Определение класса эквивалентности по одному представителю позволяет вместо всех элементов множества изучать совокупность отдельных представителей из классов эквивалентности. Например, отношение эквивалентности «иметь одинаковое число вершин», заданное на множестве многоугольников, порождает разбиение этого множества на классы треугольников, четырехугольников, пятиугольников и т.д. Свойства, присущие некоторому классу, рассматриваются на одном его представителе.
В-третьих, разбиение множества на классы с помощью отношения эквивалентности используется для введения новых понятий. Например, понятие «пучок прямых» можно определить как то общее, что имеют параллельные между собой прямые.
Другим важным видом отношений являются отношения порядка.
Определение. Отношение R на множестве X называется отношением порядка, если оно одновременно обладает свойствами антисимметричности и транзитивности.
Примерами отношений порядка могут служить: отношение «меньше» на множестве натуральных чисел; отношение «короче» на множестве отрезков, поскольку они антисимметричны и транзитивны.
Если отношение порядка обладает еще свойством связанности, то говорят, что оно является отношением линейного порядка.
Например, отношение «меньше» на множестве натуральных чисел является отношением линейного порядка, так как обладает свойствами антисимметричности, транзитивности и связанности.
Определение. Множество X называется упорядоченным, если на нем задано отношение порядка.
Так, множество N натуральных чисел можно упорядочить, если задать на нем отношение «меньше».
Если отношение порядка, заданное на множестве X, обладает свойством связанности, то говорят, что оно линейно упорядочивает множество X.
Не следует думать, что все отношения делятся на отношения эквивалентности и отношения порядка. Существует огромное число отношений, не являющихся ни отношениями эквивалентности, ни отношениями порядка.
Упражнения
1.На множестве Xпрямоугольников (рис. 107) задано отношение «иметь равные площади». Постройте граф отношения и докажите, что оно является отношением эквивалентности. Какие классы эквивалентности порождает это отношение на множестве X«?
