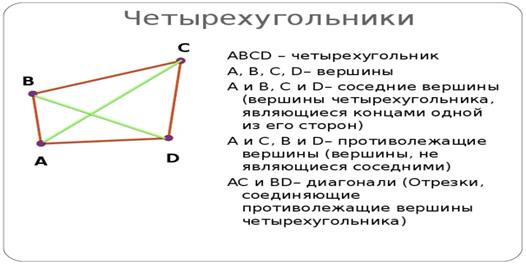
Докажите что параллелограмм противоположные стороны равны и противоположные углы равны

Параллелограмм

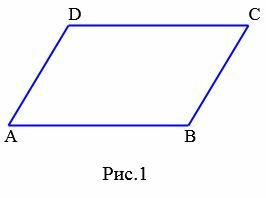
Определение 1. Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны.

Свойства параллелограмма

Свойство 1. В параллелограмме противоположные углы равны и противоположные стороны равны.

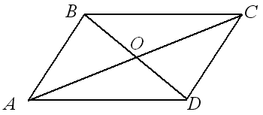
Доказательство. Рассмотрим параллелограмм ABCD (Рис.2).

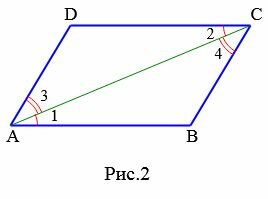Диагональ AC разделяют параллелограмм на два треугольника ACB и ACD. \( \small \angle 1=\angle 2 \) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC (см. теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично \( \small \angle 3=\angle 4 \), если рассмотреть параллельные прямые AD и BC пересеченные секущей AC. Тогда треугольники ACB и ACD равны по одной стороне и двум прилежащим углам: AC общая, \( \small \angle 1=\angle 2 \), \( \small \angle 3=\angle 4 \) (см. статью Треугольники. Признаки равенства треугольников). Поэтому \( \small AB=CD, \;\; AD=BC, \;\; \angle B=\angle D. \)

Из рисунка Рис.2 имеем: \( \small \angle A=\angle 1+\angle 3, \;\; \angle C=\angle 2+\angle 4. \) Учитывая, что \( \small \angle 1=\angle 2 \) и \( \small \angle 3=\angle 4 \), получим: \( \small \angle A=\angle C. \)

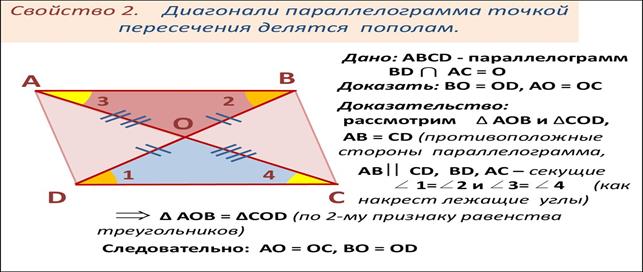
Свойство 2. Диагонали параллелограмма точкой пересечения разделяются пополам.

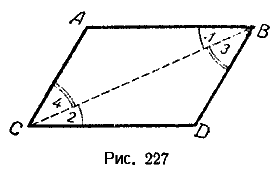
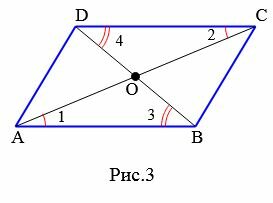
Доказательство. Рассмотрим параллелограмм ABCD (Рис.3) и пусть O точка пересечения диагоналей AC и BD. \( \small \angle 1=\angle 2 \) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC. \( \small \angle 3=\angle 4 \), если рассмотреть параллельные прямые AB и CD пересеченные секущей BD. Поскольку в параллелограмме противоположные стороны равны: AB=CD (Свойство 1), то треугольники ABO и CDO равны по стороне и прилежашим двум углам. Тогда AO=OC и BO=OD.

Признаки параллелограмма

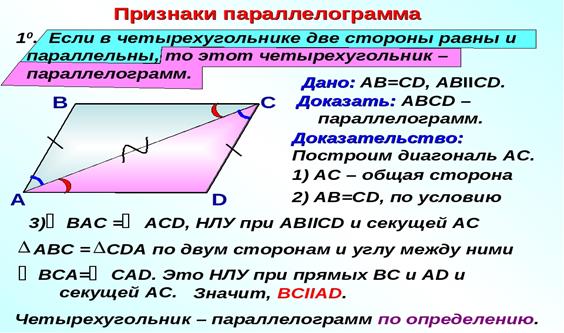
Признак 1. Если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник является параллелограммом.

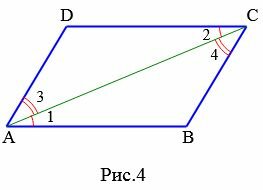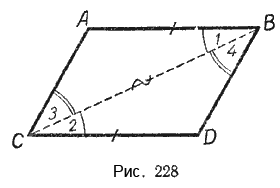
Доказательство. Рассмотрим параллелограмм ABCD. Пусть AB=CD и AB || CD. Проведем диагональ AC (Рис.4). Поскольку AB || CD, то \( \small \angle 1=\angle 2 \) как накрест лежащие углы − при рассмотрении параллельных прямых AB и CD пересеченных секущей AC. Тогда треугольники ACB и ACD равны, по двум сторонам и углу между ними. Действительно, AB=CD, AC− общая сторона \( \small \angle 1=\angle 2 \). Но тогда \( \small \angle 3=\angle 4. \) Рассмотрим прямые AD и BC, пересеченные секущей AC. Поскольку \( \small \angle 3 \) и \( \small \angle 4 \) являются накрест лежашими углами, то по теореме 1 статьи Параллельные прямые. Признаки параллельности прямых, эти прямые параллельны. Таким образом, в четырехугольнике противоположные стороны попарно параллельны (AB || CD, AD || BC) и, значит, данный четырехугольник параллелограмм.

Признак 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник является параллелограммом.

Доказательство. Рассмотрим параллелограмм ABCD (Рис.4). Проведем диагональ AC (Рис.4). Рассмотрим треугольники ACB и ACD. Эти треугольники равны по трем сторонам (см. статью Треугольники. Признаки равенства треугольников). Действительно. AC − общая для этих треугольников и по условию AB = CD, AD = BC. Тогда \( \small \angle 1=\angle 2 \). Отсюда следует AB || CD. Имеем, AB = CD, AB || CD и по признаку 1 четырехугольник ABCD является параллелограммом.

Признак 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения разделяются пополам, то данный четырехугольник − параллелограмм.

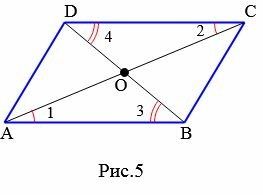Доказательство. Рассмотрим четырехугольник ABCD (Рис.5). Пусть диагонали четырехугольника пересекаются в точке O и точкой пересечения делятся пополам:

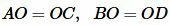Углы AOB и COD вертикальные, следовательно \( \small \angle AOB=\angle COD \). Тогда треугольники AOB и COD равны по двум сторонам и углу меду ними:

,

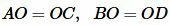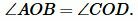Тогда AB = CD и \( \small \angle 1=\angle 2 \). Но по признаку параллельности прямых следует, что AB || CD (теорема 1 статьи Параллельные прямые. Признаки параллельности прямых). Получили:

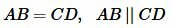и, по признаку 1 четырехугольник ABCD − параллелограмм.

Источник

Параллелограмм — признаки и свойства

Клод Бернард однажды сказал:

«Думать, что всё знаешь, останавливает тебя от того, чтобы учиться новому»

Давай узнаем что-то новое сегодня, разбирая, казалось бы, такую простую тему!

Статья поможет тебе окончательно разобраться с самыми «популярными» параллелограммами, а наши вебинары дадут тебе необходимую практику.

И на ЕГЭ ты сможешь решить любую задачу на эту тему!

Параллелограмм — коротко о главном

Параллелограмм – четырехугольник, противоположные стороны которого попарно параллельны.

Свойства параллелограмма:

Прямоугольник – четырехугольник, все углы которого прямые: \( \displaystyle \angle A=\angle B=\angle C=\angle D=90<>^\circ \).

Свойства прямоугольника:

Ромб – четырехугольник, все стороны которого равны между собой: \( \displaystyle AB=BC=CD=DA\).

Свойства ромба:

Квадрат – четырехугольник, у которого все стороны равны между собой, а все углы – прямые: \( \displaystyle AB=BC=CD=DA\); \( \displaystyle \angle A=\angle B=\angle C=\angle D=90<>^\circ \).

Свойства квадрата:

\( \displaystyle ABCD\) – ромб

Источник

Параллелограмм, его признаки и свойства

Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.

Теоремы (свойства параллелограмма):

В параллелограмме противоположные стороны равны и противоположные углы равны: , , ,.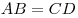

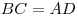
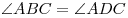
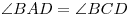
Диагонали параллелограмма точкой пересечения делятся пополам: , .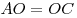

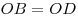
Углы, прилежащие к любой стороне, в сумме равны .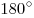

Диагонали параллелограмма делят его на два равных треугольника.

Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон: .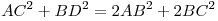

Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм.

Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Середины сторон произвольного (в том числе невыпуклого или пространственного) четырехугольника 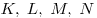являются вершинами параллелограмма Вариньона.

Стороны этого параллелограмма параллельны соответствующим диагоналям четырехугольника . Периметр параллелограмма Вариньона равен сумме длин диагоналей исходного четырехугольника, а площадь параллелограмма Вариньона равна половине площади исходного четырехугольника.

Источник

Признаки параллелограмма

Теорема 1. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.

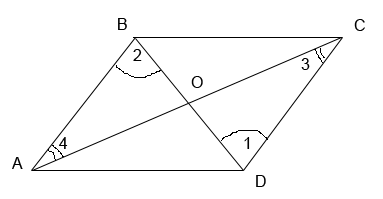
Пусть в четырёхугольнике AВDС (рис. 227) АВ = СD и АС = ВD. Докажем, что при этом условии АВ || СD и АС || ВD, т. е. четырёхугольник АВDC — параллелограмм.

Соединим отрезком какие-нибудь две противоположные вершины этого четырёхугольника, например С и В. Четырёхугольник ABDС разбился на два равных треугольника: \(\Delta\)СAВ и \(\Delta\)СDВ. В самом деле, сторона СВ у них общая, AB = СD и АС = ВD по условию. Таким образом, три стороны одного треугольника соответственно равны трём сторонам другого, поэтому \(\Delta\)СAВ = \(\Delta\)СDВ.

В равных треугольниках против равных сторон лежат равные углы, поэтому

Углы 1-й и 2-й являются внутренними накрест лежащими углами при пересечении прямых AB и СD прямой СВ. Следовательно, AB || СD.

Точно так же углы 3-й и 4-й являются внутренними накрест лежащими углами при пересечении прямых CA и ВD прямой СВ, следовательно, CA || ВD.

Теорема 2. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.

Пусть в четырёхугольнике ABDС AB = СD и AB || СD. Докажем, что при этих условиях четырёхугольник ABDС — параллелограмм (рис. 228).

Соединим отрезком СВ вершины С и В. Вследствие параллельности прямых AB и СD углы 1 и 2, как углы внутренние накрест лежащие, равны.

Тогда треугольник СAB равен треугольнику СDВ, так как сторона СВ у них общая,

AB = СD по условию теоремы и ∠1 = ∠2 по доказанному.

Из равенства этих треугольников вытекает равенство углов 3 и 4, так как они лежат против равных сторон в равных треугольниках.

Но углы 3 и 4 — это внутренние накрест лежащие углы, образованные при пересечении прямых АС и ВD прямой СВ, следовательно, АС || ВD, т. е. четырёхугольник ABDС — параллелограмм.

Теорема 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник будет являться параллелограммом.

Рассмотрим четырехугольник ABCD. Проведем в нем две диагонали AC и BD, которые будут пересекаться в точке О и делятся этой точкой пополам.

Следовательно, AB = CD и ∠1 = ∠2. Из равенства углов 1 и 2 имеем, что AB || CD.

Тогда имеем, что в четырехугольнике ABCD стороны AB = CD и AB || CD, и по первому признаку параллелограмма четырехугольник ABCD будет являться параллелограммом.

Признаки параллелограмма кратко:

1. Противоположные стороны попарно равны

2. Противоположные стороны равны и параллельны

3. Диагонали пересекаются и в точке пересечения делятся пополам

Источник

Докажите,что в параллелограмме противоположные стороны и углы равны

3. Приведите примеры букв, обладающих центром симметрии.

О Н Х Ж

Практика

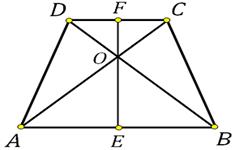
Постройте равнобедренную трапецию и проведите её оси симметрии.

Найдите сумму углов выпуклого пятиугольника.

угол В=120 сумма углов А+В=180 по определению ромба как параллелограмма. угол А=180-120=60. Диагональ BD делит ромб на два равных равносторонних треугольника, с длиной стороны 8см.

Периметр ромба равен 32 см.

Билет 2

Какой многоугольник называется выпуклым? Объясните, какие углы называются углами выпуклого многоугольника.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины

Углом выпуклого многоугольника при заданной вершине называется угол, образованный его сторонами, сходящимися в этой вершине.

2) Докажите, что в параллелограмме диагонали точкой пересечения делятся пополам

3)Приведите примеры букв, обладающих горизонтальной осью симметрии.

Практика

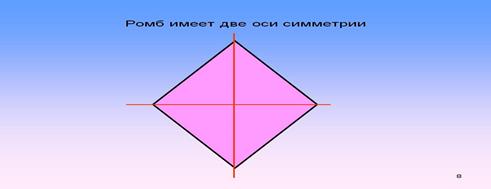
1) Постройте ромб и проведите, его оси симметрии.

2) Найдите сумму углов выпуклого семиугольника.

Билет №3

Теория

Выведите формулу для вычисления суммы углов выпуклого n-угольника.

Разобьем многоугольник на треугольники с общей вершиной О для каждого треугольника.

Получится n треугольников.

Рассмотрим один треугольник.

Сумма углов при его основании равна 180º – α1, где α1 это угол при вершине О треугольника.

Тогда, для следующего треугольника сумма углов при основании равна 180º – α2.

Общая сумма углов при основаниях n треугольников равна:

Сумма углов при вершине О равна 360º.

Поэтому α1 + α2 + α3 + … + αn = 360º.

Докажите, что если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм

Начертите четырёхугольник и покажите его диагонали, противоположные стороны и противоположные вершины.

Практика

1) 1. Приведите примеры букв, обладающих вертикальной осью симметрии.

2) 2. Найдите сумму углов выпуклого четырехугольника.

3. Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых на 30 0 меньше другого.

х+х+30+90=180

2х+120=180

2х=60

1 угол = 30 градусов, тогда 2 угол 2х30=60

Поскольку ромб это параллелограмм то он имеет все свойства параллелограмма, соответственно противолежащие углы равны. Тоесть, если 1 угол равен 30, то противолежащий угол тоже равен 30 градусов. С 2 углом тоже самое. Ответ: 30, 60, 30, 60.

Такс, в ромбе диагональ выполняет функцию биссектрисы, значит 2х30=60, 2х60=120, потому что биссектриса делит углы пополам.

Билет 4

1.Дайте определение параллелограмма. Является ли параллелограмм выпуклым четырёхугольником?

Источник