Докажите что площадь прямоугольной трапеции описанной около окружности равна произведению основания

Докажите что площадь прямоугольной трапеции описанной около окружности равна произведению основания

Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.

$$ 4.<2>^<○>$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).

$$ 4.<3>^<○>$$. В равнобокой трапеции углы при основании равны (рис. 22).

$$ 4.<4>^<○>$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).

$$ 4.<5>^<○>$$. В равнобокой трапеции диагонали равны (рис. 24).

$$ 4.<6>^<○>$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме

(рис. 25, основания равны `a` и `b`, `a>b`).

$$ 4.<7>^<○>$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).

$$ 4.<8>^<○>$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).

Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.

$$ 4.<10>^<○>$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).

$$ 4.<11>^<○>$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.

Применяем теорему косинусов (см. рис. 29а и б):

`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,

`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).

Проводим `CK«|\|«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:

В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем

Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.

Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то

Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.

Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна

Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).

Найти радиус окружности, описанной около этой трапеции.

Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда

$$ 4.<12>^<○>$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.

Источник

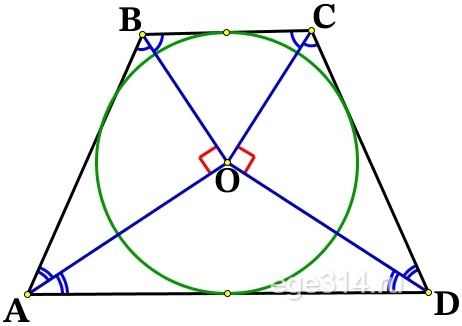
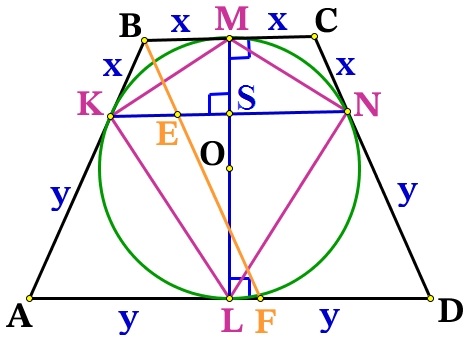
Решение №2566 Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.

Около окружности с центром О описана трапеция ABCD с основаниями AD и ВС.

а) Докажите, что ∠AOB = ∠COD = 90°.
б) Найдите отношение большего основания трапеции к меньшему, если известно, что АВ = CD, а площадь четырёхугольника с вершинами в точках касания окружности со сторонами трапеции составляет \frac<12> <49>площади трапеции ABCD.

Источник: Ященко ЕГЭ 2022 (36 вар)

Окружность вписана в углы: ∠ВAD, ∠ADC, ∠DCB и ∠CBA. Центр окружности, которая вписана в угол, расположен на биссектрисе этого угла, значит АО, DO, СО, ВО – биссектрисы и делят соответствующие углы пополам.

∠ВAD + ∠CBA = 180°
∠ADC + ∠DCB = 180°

Как односторонние углы, при параллельных прямых AD||ВС (основания трапеции) и секущих AB и СD соответственно.
Зная о биссектрисах поделим всё на 2:

Рассмотрим треугольники ΔАВО и ΔDCO, сумма углов любого треугольника равна 180°, тогда:

∠AOB = ∠COD = 90°

Что и требовалось доказать.

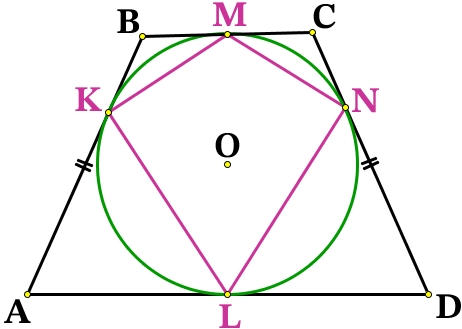
б) Найти: \frac , если АВ = СD, S_=\frac<12><49>\cdot S_ :

Отрезки касательных к окружности, проведённые из одной точки, равны:

BM = BK
CM = CN
AK = AL
DL = DN

Т.к. AB = CD, то:

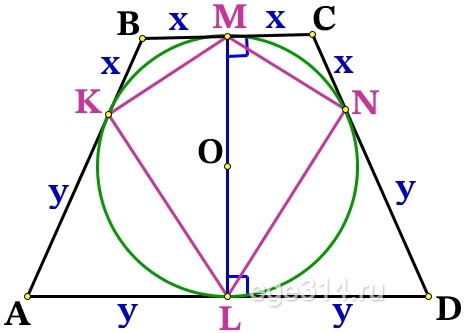
BK = СN = BM = CM = x
AK = DN = AL = DL = y

Проведём радиусы из точки О к касательным ВС и AD, тогда ОМ⊥ВС, OL⊥AD, точка О∈OM, O∈OL, значит МL это одна прямая и высота трапеции:

Проведём ещё одну высоту трапеции СН:

HD = LD – LH = y – x

Из прямоугольного ΔСHD по теореме Пифагора найдём СН:

СН 2 + HD 2 = CD 2
CH 2 + (y – x) 2 = (y + x) 2
CH 2 = (y + x) 2 – (y – x) 2 = y 2 + 2xy + x 2 – y 2 + 2xy – x 2 = 4xy
CH=\sqrt<4xy>=2\sqrt

Выразим площадь S_{ABCD :}

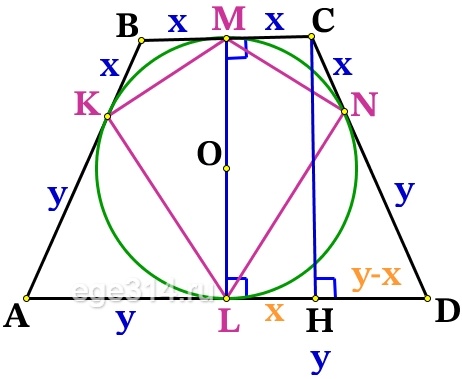
В четырёхугольнике проведём KMNL диагональ KN, прямые ВС и KN отсекают равные отрезки ВК = СN = x, значит они по теорема Фалеса параллельны ВС||KN, т.к. BC⊥LM, то KM⊥ML, значит угол между диагоналями ∠MSK = 90°.
Диагональ ML = 2\sqrt , как высота трапеции.
Проведём BF||CD и пересекающая KN в точке Е. BCDF – параллелограмм, значит EN = BC = 2x.

ΔАВF подобен ΔВКЕ (∠В – общий, ∠ВКЕ = ∠ВАF – соответственные). Из пропорциональности сторон найдём КЕ:

Найдём диагональ KN:

Выразим площадь S_KMNL :

S_=\frac<1><2 >\cdot ML\cdot KN\cdot \sin \angle MSK=\frac<1><2 >\cdot 2\sqrt\cdot \frac<4xy>\cdot \sin 90^<\circ>=\sqrt\cdot \frac<4xy>\cdot 1= \frac<4xy\sqrt>

Подставим выраженные площади с исходное отношение:

Т.к. у нас у большее основание, а х меньшее, то их отношение равно 6.

Источник