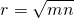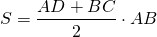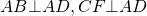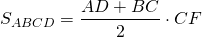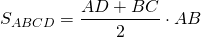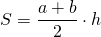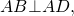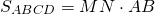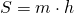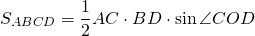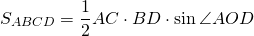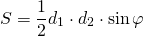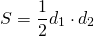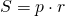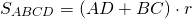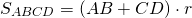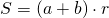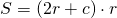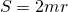Докажите что площадь прямоугольной трапеции в которую можно вписать окружность равна произведению
Узнать ещё
Знание — сила. Познавательная информация
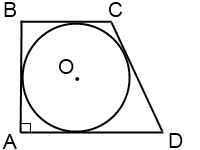
В прямоугольную трапецию вписана окружность
Если в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства.
1. Сумма оснований трапеции равна сумме боковых сторон.
2. Расстояния от вершины трапеции до точек касания вписанной окружности равны.
3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности.
4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.
5. Если точка касания делит боковую сторону на отрезки m и n, то радиус вписанной окружности равен
И еще два полезных свойства прямоугольной трапеции, в которую вписана окружность:
1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции — квадрат, сторона которого равна радиусу. (AMOE и BKOM — квадраты со стороной r).
2) Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований.
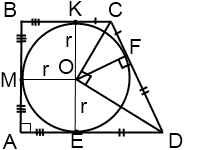
Обозначим CF=m, FD=n. Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а
Площадь прямоугольной трапеции
Площадь прямоугольной трапеции можно найти по любой из формул для площади произвольной трапеции. Некоторые из общих формул могут быть упрощены на основании свойств прямоугольной трапеции.
I. Площадь трапеции равна произведению полусуммы оснований на высоту.
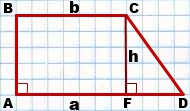
Так как меньшая боковая сторона прямоугольной трапеции перпендикулярна основаниям, то она равна высоте трапеции, то есть
Если обозначить AD=a, BC=b, CF=AB=h, то формула площади прямоугольной трапеции через основания и высоту (меньшую боковую сторону):
II. Площадь трапеции равна произведению средней линии на высоту.

Если обозначить среднюю линию MN=m, меньшую боковую сторону AB=h, получим формулу для нахождения площади прямоугольной трапеции через среднюю линию:
III. Площадь трапеции равна половине произведения диагоналей трапеции на синус угла между ними.

Если AC=d1, BD=d2, ∠COD=φ, то

VI. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.
Обозначив AD=a, BC=b, CD=c, AB=h=2r, получим формулы площади прямоугольной трапеции через радиус вписанной окружности:
Если в трапецию вписана окружность, площадь трапеции также можно найти как удвоенное произведение радиуса и средней линии. Формула
Если в прямоугольную трапецию вписана окружность, ее площадь равна произведению оснований.