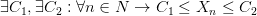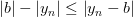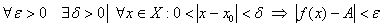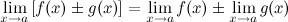Докажите что последовательность ограничена

Определение предела последовательности. Свойства сходящихся последовательностей.

Числовые последовательности.

Если каждому натуральному числу n сопоставлено в соответствие некое число x_n, то говорят, что задана числовая последовательность

Как мы видим, x_n — это функция, множеством определения которой является множество N всех натуральных чисел, а множество значенией этой функции, то есть значение всех x_n, n∈N, называют множеством значений последовательности.

Множество значений последовательности может быть как конечным, так и бесконечным, но множество ее элементов всегда бесконечно, так как любые два разных элемента последовательности отличаются своими номерами.

Последовательность может быть задана формулой, которая позволяет вычислить каждый член последовательности по ее номеру. Например, если \(x_n=\frac<\left(-1\right)^n+1>2\), то каждый нечетный член последовательности будет равен 0, а каждый четный член равен 1.

Зачастую используют реккурентный способ записи формулы последовательности, когда каждый следующий член последовательности можно найти по известным предыдущим.

Определение предела последовательности.

Записать с помощью логических символов отрицания следующих утверждений:

Пользуясь определением: найти предел последовательности \(\\>\), если:

Пусть \(\displaystyle \lim_x_n=a,\ \lim_y_n=a\). Доказать, что последовательность
$$
x_<1>,\ y_<1>,\ x_<2>,\ y_<2>\ldots,\ x_, \ y_\ldots\label
$$
сходится и ее предел также равен a.

\(\triangle\) По определению предела для любого \(\varepsilon > 0\) существуют \(N_1=N_1(\varepsilon)\) и \(N_<2>=N_<2>(\varepsilon)\) такие, что для всех \(n\geq N_<1>\) выполняется неравенство \(|x_-a| N_<\varepsilon>\geq N_<1>\), и поэтому \(|z_-a|=|x_-a| Пример 4.

Таким образом, а—предел последовательности \(\left\\), если для каждой ε—окрестности точки а найдется номер, начиная с которого все члены последовательности принадлежат этой окрестности, так что вне этой окрестности либо нет ни одного члена последовательности, либо содержится конечное число членов.

С помощью логических символов данное определение можно записать следующим образом

Доказать, что последовательность \(\left\\), где \(x_n=(-1)^n\), является расходящейся.

Единственность предела последовательности.

Числовая последовательность может иметь только один предел.

Предположим, что \(\left\\) имеет два различных предела a и b, причем a Рис. 4.2

Выберем ε > 0 таким, чтобы ε—окрестности точек a и b не пересекались, то есть не имели общих точек. Возьмем, например, ε = (b − a)/3. Так как число a—предел последовательности <x_n>, то по заданному ε > 0 можно найти номер N такой, что \(x_n\in U_\varepsilon(a)\) для всех n > N. поэтому вне интервала \(U_\varepsilon(a)\) может оказаться лишь конечное число членов последовательности. В частности, интервал \(U_\varepsilon(b)\) может содержать лишь конечное число членов последовательности. Но это противоречит тому, что b—предел последовательности, так как согласно определению предела, любая окрестность точки b должна содержать бесконечное число членов последовательности. Данное противоречие показывает, что последовательность не может иметь два различных предела. Итак, сходящаяся последовательность имеет только один предел.

Ограниченность сходящейся последовательности.

Последовательность \(\left\\) называется ограниченной снизу, если существует такое число С₁, что все члены последовательности удовлетворяют условию \(x_n\geq C_1\), то есть

Последовательность \(\left\\) называется ограниченной сверху, если

Последовательность, ограниченная как сверху, так и снизу, называется ограниченной, то есть последовательность \(\left\\) называется ограниченной, если

$$ \exists \ C_1 \ \exists \ C_2: \ \forall n \ \in\mathbb \ \rightarrow C_1\leq x_n\leq C_2\label $$

Заметим, что условие \eqref равносильно следующему

$$ \exists \ C > 0: \ \forall n\in\mathbb\rightarrow\left|x_n\right|\leq C\label $$

Геометрически ограниченность последовательности означает, что все члены последовательности содержатся в С-окрестности точки нуль.

Если последовательность имеет предел, то она ограничена.

В силу теоремы 2 всякая сходящаяся последовательность является ограниченной. Обратное неверно: не всякая ограниченная последовательность является сходящейся. Например, последовательность \(\left\<\left(-1\right)^n\right\>\) ограничена, но не является сходящейся.

Доказать, что последовательность \(\left\<<\textstyle\frac1>\right\>\) является ограниченной, если \(\undersety_n=b, \ b\neq0, \ y_n\neq0 \ для \ всех \ n\in\mathbb\).

Теорема о трех последовательностях или теорема о пределе «зажатой» последовательности.

Если последовательности \(\, \ \, \ \\) таковы, что

$$x_n\leq y_n\leq z_n \ для \ всех \ n\geq N_0,\label$$

то последовательность \(\\) сходится и \(\undersety_n=a\).

По определению предела для любого \(\varepsilon > 0\) найдутся номера \(N_1=N_1(\varepsilon) \ и \ N_2=N_2(\varepsilon)\) такие, что \(x_n\in U_\varepsilon(a)\) при всех \(n\geq N_1\) и \(z_n\in U_\varepsilon(a)\) при всех \(n\geq N_2\).

Рис. 4.3

Отсюда и из условия \eqref следует, что при всех n ≥ N, где N = max(N₀, N₁, N₂), выполняется условие \(y_n\in U_\varepsilon(a)\). Это означает, что существует \(\undersety_n=a\).

\(\triangle\,\)Заметим, что \(\sqrt[n]n-1=\alpha_n > 0\), при \(n > 1\), откуда \(n=(1+\alpha_n)^n > C_n^2\alpha_n^2,\) где\(\displaystyle C_n^2=\frac2 > \frac4,\) при \(n > 2\). Следовательно, \(\displaystyle n > \frac4\alpha_n^2,\) или \(\displaystyle \alpha_n^2 0\), то \(\displaystyle 0 Пример 10.

Если \(a > 1\), то \(a=1+\alpha\), где \(\alpha > 0\), откуда \(a^n=\displaystyle \left(1+\alpha\right)^n > C_n^\alpha^\), при \(n > p\).

Пусть \(n > 2p\), тогда \(\displaystyle C_n^=\frac <(p+1)!>> \frac n<(p+1)!>\left(\frac n2\right)^p\), так как \(\displaystyle n-k > \frac n2\) при \(\displaystyle 1\leq k\leq p\). Отсюда следует, что \(\displaystyle 0 Теорема 4.

Если \(\displaystyle \lim_x_=a\) и a Следствие 2.

\(\circ\) Предположим, что неравенство \eqref не выполняется. Тогда \(a Замечание 3.

В частности, если для сходящейся последовательности \(\\>\) выполняется для всех \(n\in\mathbb\) (или для всех \(n\geq N_0)\) неравенство \(x_\geq \alpha\quad(x_ \leq\beta)\), то \(\displaystyle \lim_x_\geq \alpha\quad(\lim_ x_n\leq\beta)\). Отсюда следует, что если все члены сходящейся последовательности \(\\) принадлежат отрезку \([a,b]\), то есть \(a\leq x_n\leq b\) для всех \(n\in\mathbb\), то и предел этой последовательности принадлежит отрезку \([a,b]\), то есть \(\displaystyle a\leq\lim_x_\leq b\).

В следствии 2 утверждается, что если соответствующие члены двух сходящихся последовательностей связаны знаком нестрогого неравенства, то такое же неравенство справедливо и для пределов этих последовательностей. Короче: предельный переход сохраняет знак нестрогого неравенства. Однако знак строгого неравенства, вообще говоря, не сохраняется, то есть если \(x_n > у_n\) при \(n\geq N_0\) и последовательности \(\\>, \ \\>\) сходятся, то \(\displaystyle <\lim_x_\geq\lim_y_>\). Например, если \(x_=1+\displaystyle \frac<1>, \ y_=1-\displaystyle \frac<1>\), то \(x_n > y_, \ n\in\mathbb\quad\), но \(\displaystyle \lim_x_=\lim_y_=1\).

Источник

Ограниченность сходящейся последовательности

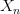
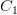
Последовательность называется ограниченной снизу, если существует такое число , что все члены последовательности удовлетворяют условию , т. е.:

Последовательность называется ограниченной сверху, если:

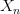
Последовательность, ограниченную как снизу, так и сверху, называют ограниченной, т. е. последовательность 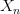называется ограниченной, если:

это можно записать и так:

Таким образом, последовательность называют ограниченной, если множество ее значений ограничено.

Теорема: ( об ограниченности сходящейся последовательности)

Если последовательность имеет предел, то она ограничена.

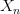
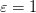
Пусть последовательность имеет предел, равный а. По определению предела для найдем номер N такой, что при всех имеет место неравенство . Так как модуль суммы не превосходит суммы модулей, то:

.

Поэтому при всех выполняется неравенство:

.

Положим , тогда при всех , т. е. последовательность ограничена.

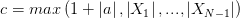
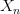
Замечание: В силу предыдущей теоремы всякая сходящаяся последовательность является ограниченной. Обратное неверно: не всякая ограниченная последовательность является сходящейся! Например, последовательность ограничена, но не является сходящейся.

Замечание: Если условие не выполняется, т. е.

,

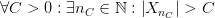
то говорят, что последовательность 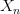не ограничена.

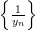
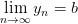
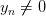
Пример: Доказать, что последовательность является ограниченной, если , и , для всех .

Так как , то . По заданному числу в силу определения предела последовательности найдется номер такой, что:

.

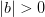
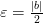
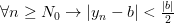
Используя неравенство для модуля разности

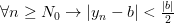
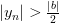
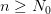
и неравенство , получаем , откуда . И поэтому для всех справедливо неравенство .

Пусть C = max , для всех выполняется неравенство , т. е. – ограниченная последовательность.

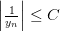
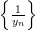
8 Основные свойства сходящихся последовательностей.

Свойства сходящихся последовательностей:

Основные свойства сходящихся последовательностей

1. Если все элементы бесконечно малой последовательности <х_n> равны одному и тому же числу с, то с = 0.

2. Сходящаяся последовательность имеет только один предел.

3. Сходящаяся последовательность ограничена.

4. Сумма (разность) сходящихся последовательностей <х_n> и <у_n> есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностей <х_n> и <у_n>.

5. Произведение сходящихся последовательностей <х_n> и <у_n> есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей <х_n> и <у_n>

6. Частное двух сходящихся последовательностей <х_n> и <у_n> при условии, что предел последовательности <у_n>отличен от нуля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей <х_n> и <у_n>.

7. Если элементы сходящейся последовательности <х_n> удовлетворяют неравенству x_n ≥ b (х_n ≤ b) начиная с некоторого номера, то и предел а этой последовательности удовлетворяет неравенству а ≥ b (а ≤ b).

8. Произведение бесконечно малой последовательности на ограниченную последовательность или на число есть бесконечно малая последовательность.

9. Произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Справедлива следующая теорема (основная теорема теории пределов): если то: ; ; при условии, что b ≠ 0 и для всех n.

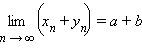
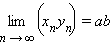
9 Подпоследовательности и их пределы. Лемма больцано-вейерштрасса.

Подпоследовательности

Определение.

Пусть задана некоторая последовательность < > и

есть строго возрастающая последовательность натуральных чисел.Тогда последовательность

называется подпоследовательностью последовательности < >.

Пример.
Пусть задана последовательность

Запишем некоторые ее подпоследовательности:

;

;

;
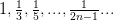
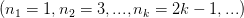
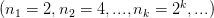
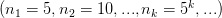
Но последовательность

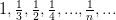
уже не является подпоследовательностью последовательности .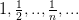

Определение.
Будем писать

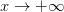
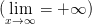
и говорить, что последовательность < > стремится к плюс бесконечности, если для каждого числа найдется номер , такой что при любом
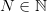
Аналогично даются определения для случая ,

Теорема Больцано — Вейерштрасса, или лемма Больцано — Вейерштрасса о предельной точке — фундаментальная теорема математического анализа, гласящая, что из любой ограниченной последовательности точек пространства 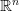можно выделитьсходящуюся подпоследовательность. Т. Б. — В., используется при доказательстве многих теорем анализа, например, теоремы о достижении непрерывной на отрезке функцией своих точных верхней и нижней граней. Теорема названа в честь чешского математикаБернарда Больцано и немецкого математика Карла Вейерштрасса, которые независимо друг от друга вывели ее формулировку и доказательство.

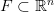
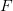
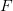
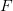
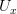
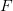
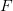
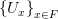
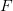
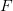
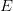
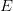
Формулировка.Любое бесконечное ограниченное множество имеет по крайней мере одну предельную точку. Доказательство. Пусть множество является бесконечным и ограниченным множеством. Предположим, что оно не имеет предельных точек. Следовательно, оно является замкнутым. Поскольку еще и ограничено, то, по теореме Гейне – Бореля, компактно. Для каждой точки построим такую окрестность , в которой нет других точек из , кроме (если бы для какой-то точки такой окрестности не было, то эта точка была бы предельной для ). Тогда семейство образуетоткрытое покрытие компактного множества . Пользуясь компактностью , выберем из него некое конечное подпокрытие, иными словами. конечный набор шаров, в каждом из которых содержится лишь по одной точке из множества . Но это противоречит тому, что множество бесконечно.
Замечание. Предельная точка, существование которой утверждается в данной теореме, вообще говоря, не обязана принадлежать множеству .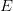

10 Определение пределов функции по коши и гейне.

Предел функции по Гейне: число называется пределом функции в точке , если для любой последовательности точек (принадлежащих и отличных от ), которая сходится к точке , соответствующая последовательность значений функции сходится к .

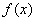
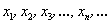
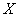
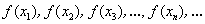
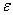
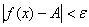
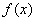
Второе определение предела соорудил… да-да, вы правы. Но сначала разберёмся в его конструкции. Рассмотрим произвольную -окрестность точки («чёрная» окрестность). По мотивам предыдущего параграфа, запись означает, чтонекоторое значение функции находится внутри «эпсилон»-окрестности.

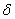
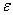
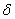
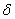
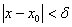
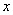
Теперь найдём -окрестность, которая соответствует заданной -окрестности(мысленно проводим чёрные пунктирные линии слева направо и затем сверху вниз). Обратите внимание, что значение выбираетсяпо длине меньшего отрезка, в данном случае – по длине более короткого левого отрезка. Более того, «малиновую» -окрестность точки можно даже уменьшить, поскольку в нижеследующем определенииважен сам факт существования этой окрестности. И, аналогично, запись означает, что некоторое значение находится внутри «дельта»-окрестности.

Предел функции по Коши: число называется пределом функции в точке , если для любой заранее выбранной окрестности (сколь угодно малой),существует -окрестность точки , ТАКАЯ, что: КАК ТОЛЬКО значения (принадлежащие ) входят в данную окрестность: (красные стрелки) – ТАК СРАЗУ соответствующие значения функции гарантированно зайдут в -окрестность: (синие стрелки).

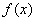
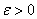
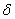
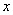
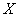
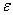
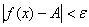
Должен предупредить, что в целях бОльшей доходчивости я немного сымпровизировал, поэтому не злоупотребляйте =)

Короткая запись: , если

В чём суть определения? Образно говоря, бесконечно уменьшая 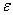-окрестность, мы «сопровождаем» значения функции до своего предела, не оставляя им альтернативы приближаться куда-то ещё. Довольно необычно, но опять же строго! Чтобы как следует проникнуться идеей, перечитайте формулировку ещё раз.

! Внимание: если вам потребуется сформулировать только определение по Гейне или только определение по Коши, пожалуйста, не забывайте о существенномпредварительном комментарии: «Рассмотрим функцию , которая определена на некотором промежутке за исключением, возможно, точки ». Я обозначил это единожды в самом начале и каждый раз не повторял.

11 Свойства пределов функции.

1° Предел суммы/разности двух функций равен сумме/разности их пределов:

2° Предел произведения двух функций равен произведению их пределов:

3° Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю:

4° Константу можно выносить за знак предела:

5° Предел степени с натуральным показателем равен степени предела:

Источник