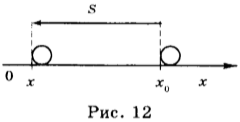
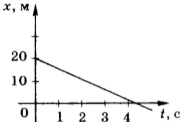
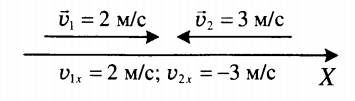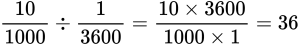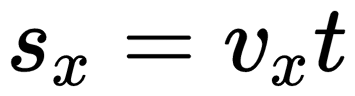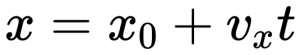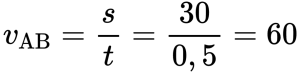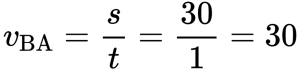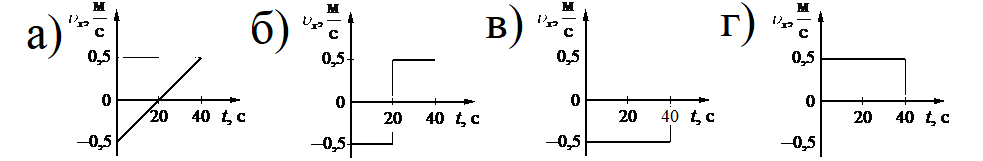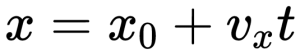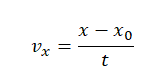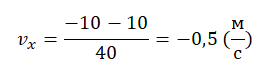Докажите что при равномерном прямолинейном движении точки в плоскости x0y
Равномерное прямолинейное движение
теория по физике 🧲 кинематика
Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.
Скорость при прямолинейном равномерном движении
Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.
Векторный способ записи скорости при равномерном прямолинейном движении: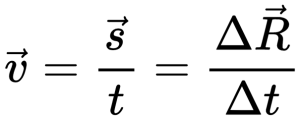
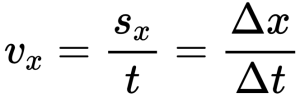
Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.
Спидометр — прибор для измерения модули скорости тела.
График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:
Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.
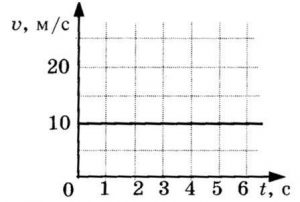
Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.
График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:
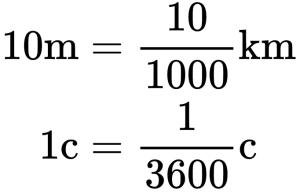
Перемещение и координаты тела при равномерном прямолинейном движении
Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.
При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:
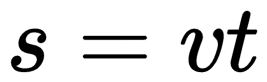
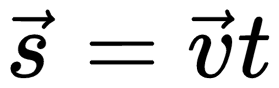
При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.
Формула проекции перемещения:
График проекции перемещения
График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:
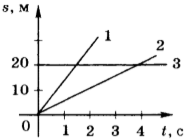
Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси sx.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси sx меньше.
График координаты
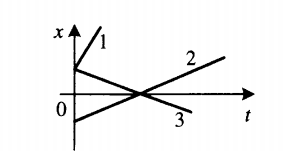
График координаты представляет собой график зависимости координаты от времени. Выглядит он так:
Так как график координаты представляет собой график линейной функции, уравнение координаты принимает вид :
Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.
Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.
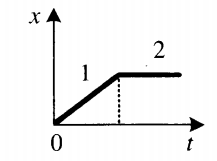
Пример №2. График зависимости координаты тела от времени имеет вид:
Изучите график и на его основании выберите два верных утверждения:
На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.
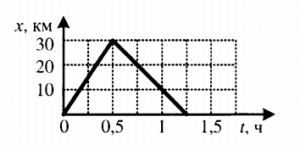
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?
Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:
Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:
Скорость во время движения от В к А равна:
Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.
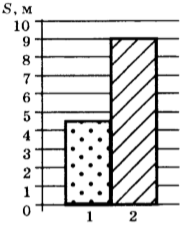
На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v2 больше скорости первого тела v1 в n раз, где n равно…
Алгоритм решения
Решение
Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:
Скорость определяется формулой:
Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:
Скорость первого тела:
Скорость второго тела:
Отношение скорости второго тела к скорости первого тела:
pазбирался: Алиса Никитина | обсудить разбор | оценить
На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении тела по оси Ox.
Алгоритм решения
Уравнение координаты при равномерном прямолинейном движении имеет вид:
Отсюда проекция скорости равна:
Начальная координата xo = 10 м, конечная x = –10 м. Общее время, в течение которого двигалось тело, равно 40 с.
Вычисляем проекцию скорости:
Этому значению соответствует график «в».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Весь график можно поделить на 3 участка:
По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t1 = 20 c до t2 = 50 с. Этому времени соответствуют два участка:
Записываем формулу искомой величины:
s1 — путь тела, пройденный на первом участке, s2 — путь тела, пройденный на втором участке.
s1и s2 можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:
Теперь рассчитаем пути s1и s2, а затем сложим их:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Равномерное прямолинейное движение
1. Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Слова «любые равные» означают, что за каждый час, за каждую минуту, за каждые 30 минут, за каждую секунду, за каждую долю секунды тело совершает одинаковые перемещения.
Равномерное движение — идеализация, поскольку практически невозможно создать такие условия, чтобы движение тела было равномерным в течение достаточно большого промежутка времени. Реальное движение может лишь приближаться к равномерному движению с той или иной степенью точности.
2. Изменение положения тела в пространстве при равномерном движении может происходить с разной быстротой. Это свойство движения — его «быстрота» характеризуется физической величиной, называемой скоростью.
Скоростью равномерного прямолинейного движения называют векторную физическую величину, равную отношению перемещения ко времени, за которое это перемещение произошло.
Если за время \( t \) тело совершило перемещение \( \vec \) , то скорость его движения \( \vec >
3. Поскольку основной задачей механики является определение в любой момент времени положения тела, т.е. его координаты, необходимо записать уравнение зависимости координаты тела от времени при равномерном движении.
Полученная формула позволяет определить координату тела при равномерном движении в любой момент времени, если известны начальная координата и проекция скорости движения.
4. Зависимость координаты от времени можно представить графически.
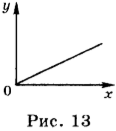
Предположим, что тело движется из начала координат вдоль положительного направления оси ОХ с постоянной скоростью. Проекция скорости на ось ОХ равна 4 м/с. Уравнение движения в этом случае имеет вид: \( x \) = 4 м/с · \( t \) . Зависимость координаты от времени — линейная. Графиком такой зависимости является прямая линия, проходящая через начало координат (рис. 13).
Для того чтобы её построить, необходимо иметь две точки: одна из них \( t \) = 0 и \( x \) = 0, а другая \( t \) = 1 с, \( x \) = 4 м. На рисунке приведён график зависимости координаты от времени, соответствующий данному уравнению движения.
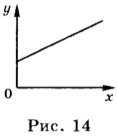
Если в начальный момент времени координата тела \( x_0 \) = 2 м, а проекция его скорости \( v_x \) = 4 м/с, то уравнение движения имеет вид: \( x \) = 2 м + 4 м/с · \( t \) . Это тоже линейная зависимость координаты от скорости, и её графиком является прямая линия, проходящая через точку, для которой \( t \) = 0, \( x \) = 2 м (рис. 14).
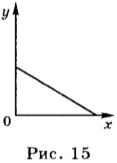
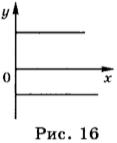
В том случае, если проекция скорости отрицательна, уравнение движения имеет вид: \( x \) = 2 м – 4 м/с · \( t \) . График зависимости координаты такого движения от времени представлен на рисунке 15.
Таким образом, движение тела может быть описано аналитически, т.е. с помощью уравнения движения (уравнения зависимости координаты тела от времени), и графически, т.е. с помощью графика зависимости координаты тела от времени.
График зависимости проекции скорости равномерного прямолинейного движения от времени представлен на рисунке 16.
5. Ниже приведён пример решения основной задачи кинематики — определения положения тела в некоторый момент времени.
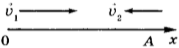
Задача. Два автомобиля движутся навстречу друг другу равномерно и прямолинейно: один со скоростью 15 м/с, другой — со скоростью 12 м/с. Определите время и место встречи автомобилей, если в начальный момент времени расстояние между ними равно 270 м.
При решении задачи целесообразно придерживаться следующей последовательности действий:
Применим эту последовательность действий к приведённой выше задаче.
Автомобили можно считать материальными точками, поскольку расстояние между ними много больше их размеров и размерами автомобилей можно пренебречь
Система отсчёта связана с Землёй, ось \( Ox \) направлена в сторону движения первого тела, начало отсчёта координаты — т. \( O \) — положение первого тела в начальный момент времени.
Начальные условия: \( t \) = 0; \( x_ <01>\) = 0; \( x_ <02>\) = 270.
Уравнения для каждого тела с учётом начальных условий: \( x_1=v_1t \) ; \( x_2=l-v_2t \) . В месте встречи тел \( x_1=x_2 \) ; следовательно: \( v_1t=l-v_2t \) . Откуда \( t=\frac
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Чему равна проекция скорости равномерно движущегося автомобиля, если проекция его перемещения за 4 с равна 80 м?
1) 320 м/с
2) 80 м/с
3) 20 м/с
4) 0,05 м/с
2. Чему равен модуль перемещения мухи за 0,5 мин., если она летит со скоростью 5 м/с?
1) 0,25 м
2) 6 м
3) 10 м
4) 150 м
1) \( v_1=v_2 \)
2) \( v_1=2v_2 \)
3) \( 2v_1=v_2 \)
4) \( 1,2v_1=10v_2 \)
1) \( v_1=v_2 \)
2) \( v_1=2v_2 \)
3) \( 3v_1=v_2 \)
4) \( 2v_1=v_2 \)
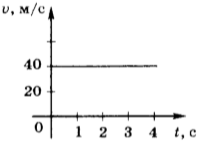
5. На рисунке приведён график зависимости модуля скорости равномерного движения от времени. Модуль перемещения тела за 2 с равен
1) 20 м
2) 40 м
3) 80 м
4) 160 м
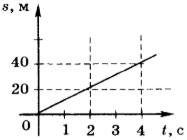
6. На рисунке приведён график зависимости пути, пройденного телом при равномерном движении от времени. Модуль скорости тела равен
1) 0,1 м/с
2) 10 м/с
3) 20 м/с
4) 40 м/с
7. На рисунке приведены графики зависимости пути от времени для трёх тел. Сравните значения скорости \( v_1 \) , \( v_2 \) и \( v_3 \) движения этих тел.
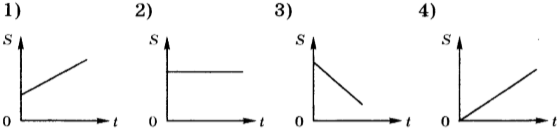
8. Какой из приведённых ниже графиков представляет собой график зависимости пути от времени при равномерном движении тела?
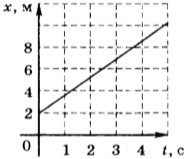
9. На рисунке приведён график зависимости координаты тела от времени. Чему равна координата тела в момент времени 6 с?
1) 9,8 м
2) 6 м
3) 4 м
4) 2 м
10. Уравнение движения тела, соответствующее приведённому в задаче 9 графику, имеет вид
1) \( x=1t \) (м)
2) \( x=2+3t \) (м)
3) \( x=2-1t \) (м)
4) \( x=4+2t \) (м)
11. Установите соответствие между величинами в левом столбце и зависимостью значения величины от выбора системы отсчёта в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ВЕЛИЧИНА
A) перемещение
Б) время
B) скорость
ЗАВИСИМОСТЬ ОТ ВЫБОРА СИСТЕМЫ ОТСЧЁТА
1) зависит
2) не зависит
12. На рисунке приведён график зависимости координаты тела от времени. Какие выводы можно сделать из анализа графика? Укажите два правильных ответа.
1) тело двигалось все время в одну сторону
2) в течение четырёх секунд модуль скорости тела уменьшался, а затем увеличивался
3) проекция скорости тела все время была положительной
4) проекция скорости тела в течение четырёх секунд была положительной, а затем — отрицательной
5) в момент времени 4 с тело остановилось
Часть 2
13. Два автомобиля движутся друг за другом равномерно и прямолинейно: один со скоростью 20 м/с, другой — со скоростью 15 м/с. Через какое время второй автомобиль догонит первый, если в начальный момент времени расстояние между ними равно 100 м?
§ 4. Равномерное прямолинейное движение. Скорость. Уравнение движения (окончание)
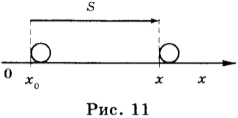
Выберем оси координат так, чтобы точка двигалась по какой-либо оси, например по оси ОХ. Тогда векторы 


Запомни
Уравнение (1.5) есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме.
Оно позволяет найти координату х точки при этом движении в любой момент времени, если известны проекция её скорости на ось ОХ и её начальная координата х0.
Если 

x = x0 + 
y = y0
z = z0,
где х0, у0, z0 — проекции радиус-вектора 

Отметим, что, строго говоря, равномерного прямолинейного движения не существует. Автомобиль на шоссе никогда не едет абсолютно прямо, небольшие отклонения в ту или иную сторону от прямой всегда имеются. И значение скорости слегка изменяется. Но приближённо на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.
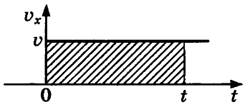
Графическое представление равномерного прямолинейного движения. Полученные результаты можно изобразить наглядно с помощью графиков. Особенно прост график зависимости проекции скорости от времени (рис. 1.11). Это прямая, параллельная оси времени. Площадь прямоугольника ОАВС, заштрихованная на рисунке, равна изменению координаты точки за время t. Ведь сторона ОА есть υx, а сторона ОС — время движения t, поэтому Δx = υxt.
На рисунке 1.12 приведены примеры графиков зависимости координаты от времени для трёх различных случаев равномерного прямолинейного движения. Прямая 1 соответствует случаю х0 = 0, υx1 > 0; прямая 2 — случаю х0 0, а прямая 3 — случаю х0 > 0, υx3 Образцы заданий ЕГЭ
A1. Зависимость координаты точки от времени при равномерном прямолинейном движении выражается
1) линейной функцией 3) тригонометрической функцией
2) квадратичной функцией 4) показательной функцией
A3. В таблице приведены координаты корабля, плывущего по прямому каналу.
Согласно данным таблицы, движение корабля является