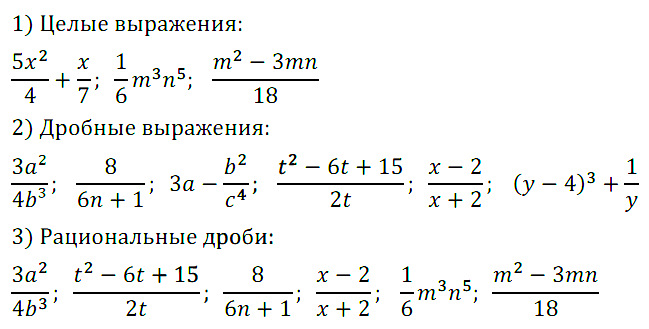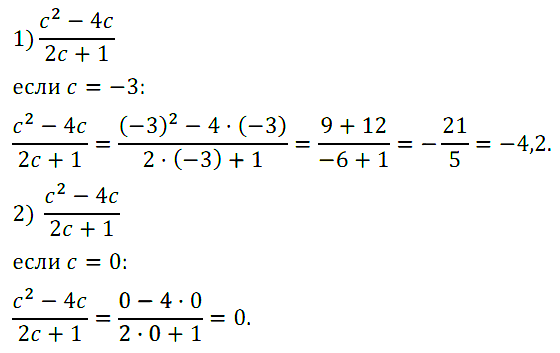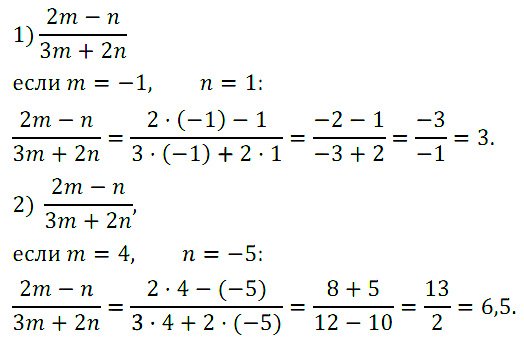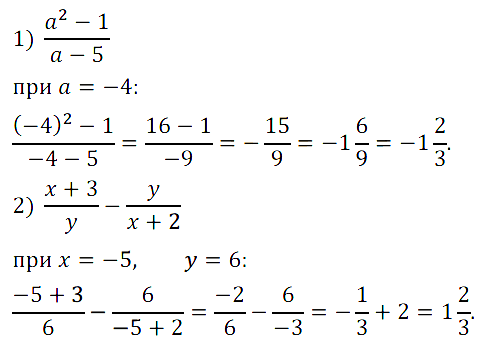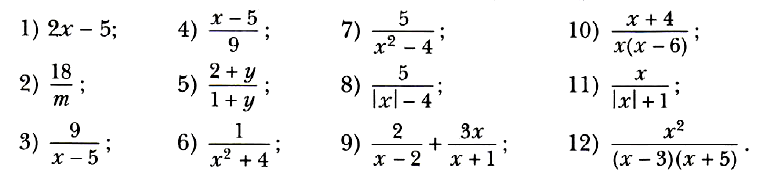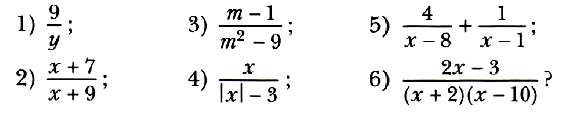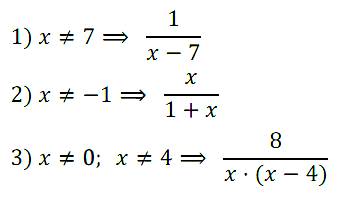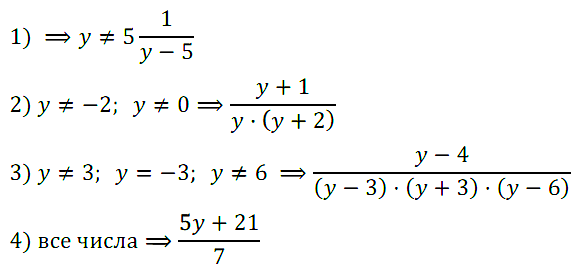Докажите что при всех допустимых значениях переменной x значение дроби отрицательное

Алгебра 8 класс Мерзляк Упражнения 1-26

Алгебра 8 класс УМК Мерзляк. Упражнения №№ 1 — 26 из учебника с ответами и решениями. Глава 1. Рациональные выражения. § 1. Рациональные дроби. Алгебра 8 Мерзляк Упражнения 1-26 + ОТВЕТЫ.

Нажмите на спойлер, чтобы посмотреть ответ на задание.

Алгебра 8 класс Мерзляк
§ 1. Упражнения №№ 1 — 26:

Задание № 2. Чему равно значение дроби (c 2 – 4c)/(2c + 1), если: 1) с = –3; 2) с = 0?

Задание № 3. Найдите значение выражения (2m – n)/(3m + 2n), если: 1) m = –1, n = 1; 2) m = 4, n = –5.

Задание № 4. Чему равно значение выражения: 1) (a 2 – 1)/(a – 5) при а = –4; 2) (х + 3)/у – у/(х + 2) при х = –5, у = 6?

Задание № 5. Найдите допустимые значения переменной, входящей в выражение:

Задание № 6. При каких значениях переменной имеет смысл выражение:

Задание № 7. Запишите рациональную дробь, которая содержит переменную х и имеет смысл при всех значениях х, кроме: 1) х = 7; 2) х = –1; 3) х = 0 и х = 4.

Задание № 8. Запишите рациональную дробь, содержащую переменную у, допустимыми значениями которой являются:
1) все числа, кроме 5; 3) все числа, кроме 3, –3 и 6;
2) все числа, кроме –2 и 0; 4) все числа.

Задание № 9. Автомобиль проехал по шоссе а км со скоростью 75 км/ч и по грунтовой дороге b км со скоростью 40 км/ч. За какое время автомобиль проехал весь путь? Составьте выражение и найдите его значение при а = 150, b = 20.

Задание № 10. Ученик купил тетради по 8 р., заплатив за них m р., и по 14 р., заплатив за них n р. Сколько тетрадей купил ученик? Составьте выражение и найдите его значение при m = 24, n = 56.

Задание № 11. Докажите, что при всех допустимых значениях переменной х значение дроби: 1) 1/x 2 положительное; 2) (x 2 + 1)/(6x – 9 – x 2 ) отрицательное.

Источник