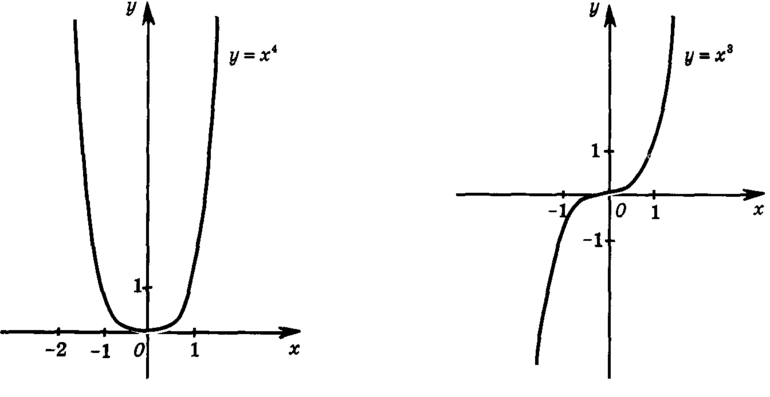Докажите что произведение четной функции на нечетную есть функция нечетная
Понятие четной и нечетной функции
Понятие четности и нечетности функции
Главное условие при исследовании функции на четность/нечетность — это симметричность области определения относительно 0. Если она не симметрична, то функция не является ни четной, ни нечетной, и дальнейшее исследование производить не нужно. Например, \(D(y)\in(-\infty;+\infty)\) симметрична относительно 0, а \(D(y):x\in(-5;9)\) — нет.
Четная функция
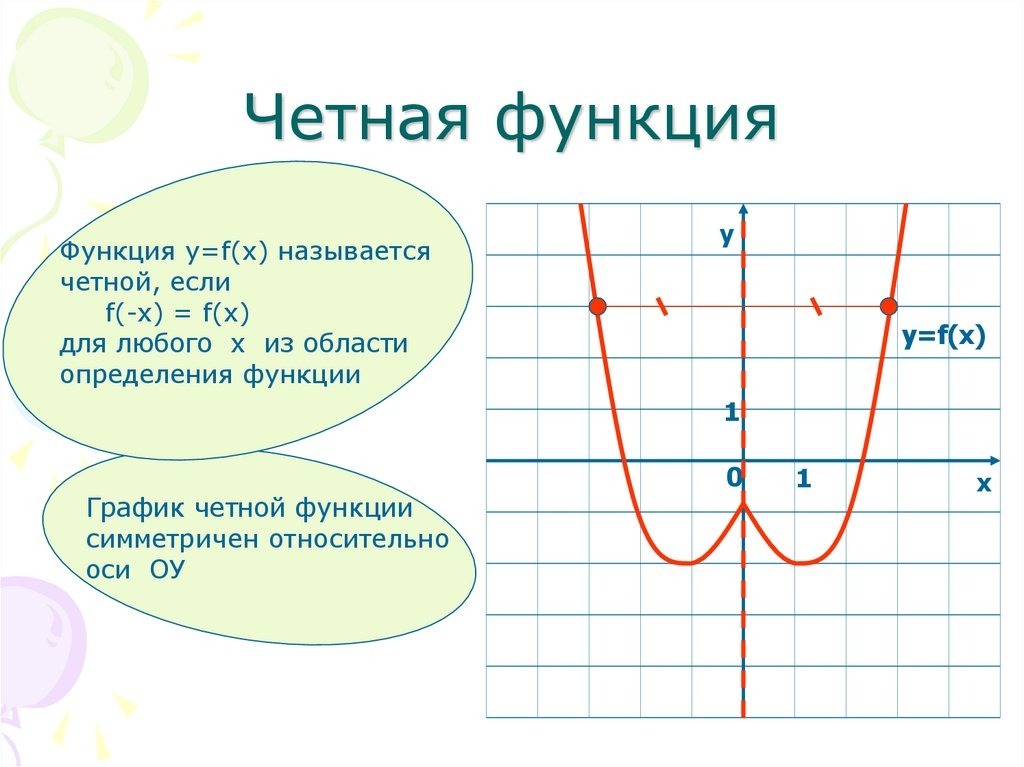
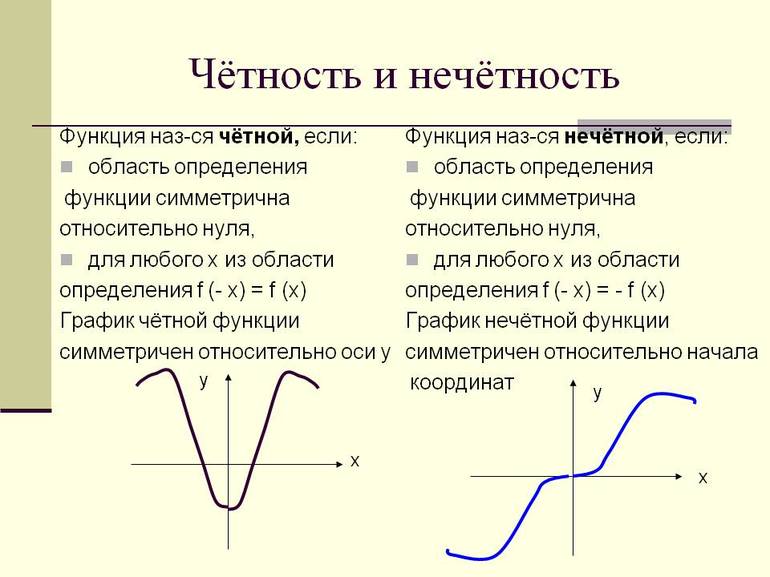
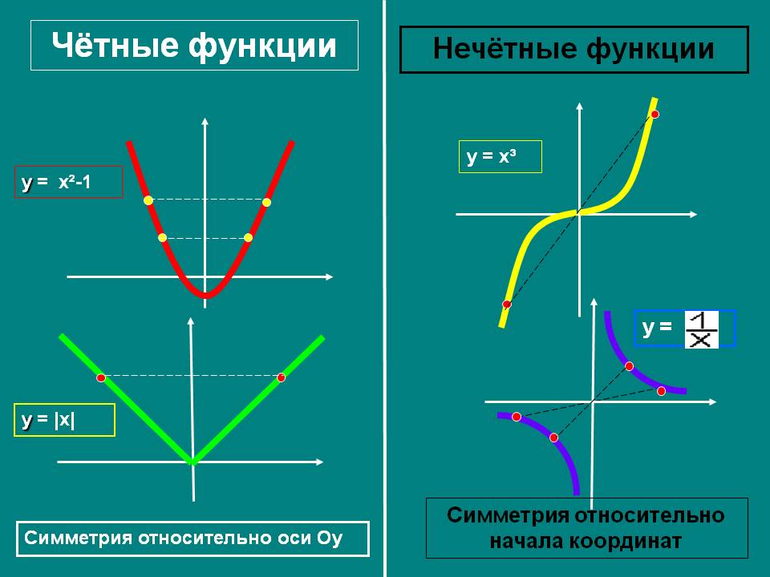
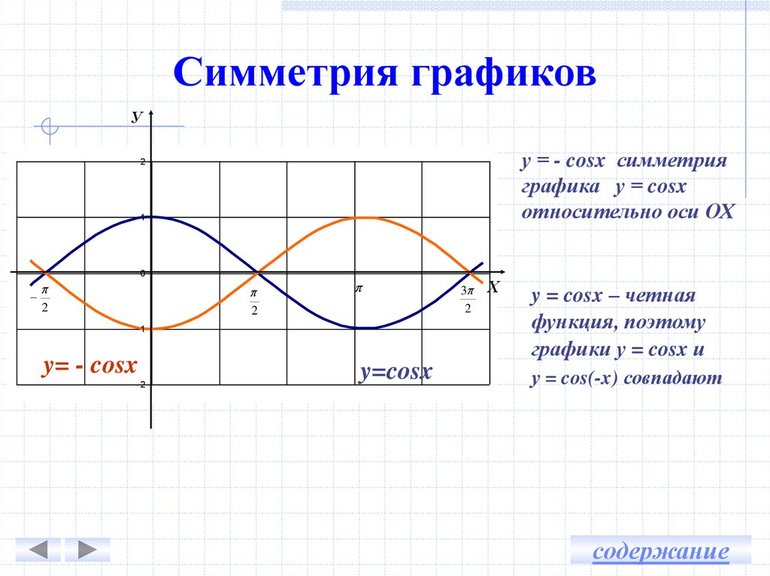
Функцию \(f(x)\) называют четной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=f(x).\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
График четной функции симметричен относительно оси Ох.
Нечетная функция
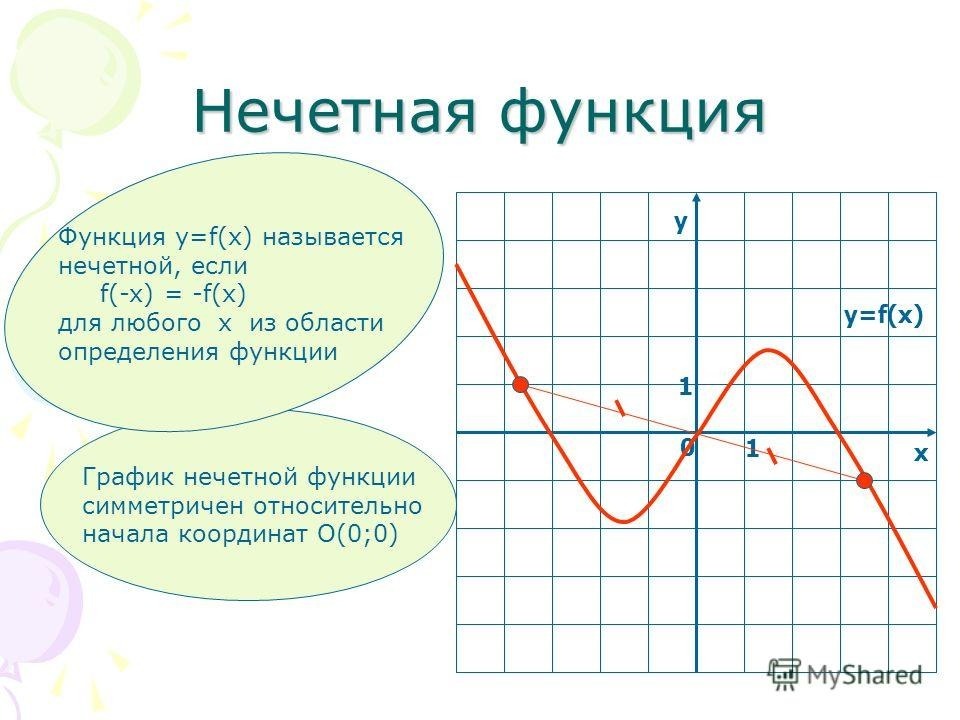
Функцию \(f(x)\) называют нечетной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=-f(x).\)
График нечетной функции симметричен относительно начала координат (точки (0;0)).
Произведение четной и нечетной функции
Произведение четной и нечетной функций есть нечетная функция.
Пусть \(f(x)\) — четная функция, а \(g(x)\) — нечетная. Тогда \(f(x)=f(-x), а g(-x)=-g(x).\)
Исследование функций в примерах
Доказать, что функция \(y=x^2\) четная.
1. Найдем область определения: \(D(y):x\in(-\infty;+\infty)\) — симметрична относительно 0.
Исследовать на четность и нечетность функцию \(f(x)=8x^3-7x.\)
1. Найдем область определения: \(D(f):x\in(-\infty;+\infty)\) — симметрична относительно 0.
Исследовать на четность и нечетность функции \(f_1(x)=\frac
Рассмотрим первую функцию:
1. Найдем область определения: x — любое число, кроме 1. Она не симметрична относительно 0, значит \( f_1(x)\) относится к функциям общего вида, то есть не является ни четной ни нечетной.
Рассмотрим вторую функцию:
Четные и нечетные функции
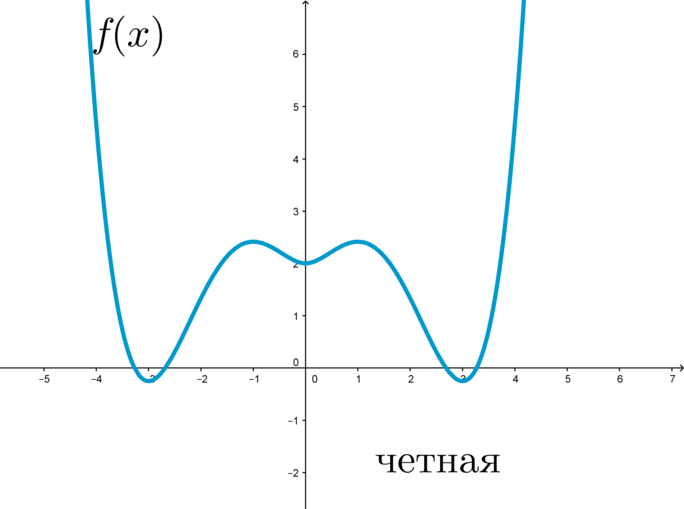
График четной функции симметричен относительно оси \(y\) :
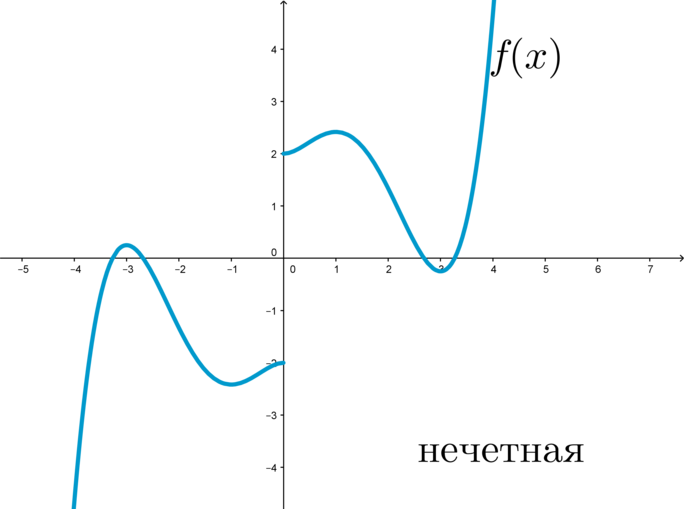
График нечетной функции симметричен относительно начала координат:
\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.
\(\blacktriangleright\) Некоторые свойства:
1) Произведение и частное двух функций одинаковой четности — четная функция.
2) Произведение и частное двух функций разной четности — нечетная функция.
3) Сумма и разность четных функций — четная функция.
4) Сумма и разность нечетных функций — нечетная функция.
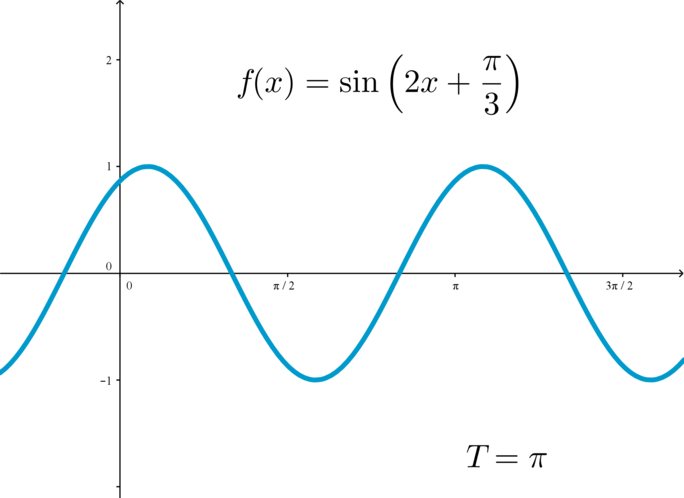
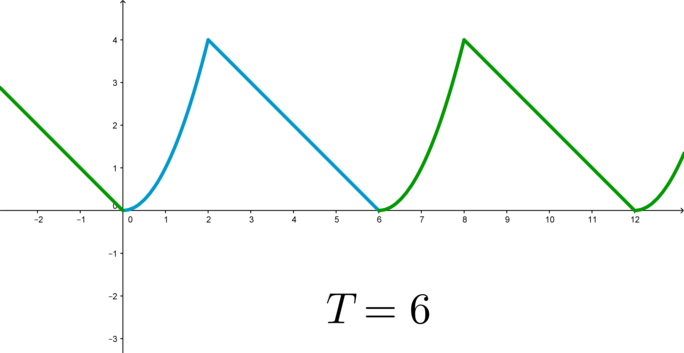
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:
При каких значениях параметра \(a\) уравнение
имеет единственное решение?
\[2\cdot 0+a\mathrm
симметричен относительно начала координат.
Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)
\(\dfrac n2, n\in\mathbb
(Задача от подписчиков)
имеет хотя бы один корень.
(Задача от подписчиков)
имеет шесть различных решений.
Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.
1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \[D=a^2-16a+52>0\quad\Leftrightarrow\quad a\in (-\infty;8-2\sqrt3)\cup(8+2\sqrt3;+\infty)\]
2) Также нужно, чтобы оба корня были положительными (так как \(t>0\) ). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: \[\begin
Общие сведения
Исследование функции на четность и нечетность — базовый элемент, показывающий ее поведение, которое зависит от значения аргумента. Последний является независимой переменной, соответствующей определенным допустимым значениям. Множество чисел, которое может принимать неизвестная независимого типа, называется областью определения. Областью значений функции вида y = f (x) являются все значения зависимой переменной «y».
Теперь следует сформулировать список базовых знаний, которые необходимы для анализа выражений на четность. Если нужно выполнить другие процедуры исследования, то его следует расширить. Например, для нахождения максимума следует ознакомиться с производной. Необходимый минимум знаний о функциях следующий:
Первый элемент необходим для выявления аргумента, при котором можно узнать его недопустимые значения, а также определить симметричность. От свойств и вида также зависит четность. Первое рекомендуется применять в частных случаях, например, произведение двух нечетных тождеств. Результат следует проверять при помощи соответствующего программного обеспечения. Например, онлайн-калькулятор четности и нечетности функций позволяет следить за правильностью решения.
Область определения
Первый элемент, который нужен для анализа, следует рассмотреть подробнее. Область определения функции z = g (y) специалисты рекомендуют обозначать литерой «D». Полная запись выглядит таким образом: D (z). Кроме того, следует выяснить симметричность множества. Под последним понимается некоторый интервал, который нужно найти.
D (z) записывается в виде множества. Например, D (z) = [1;8]. Запись значит ограниченность аргумента, принимающего значения от 1 включительно до 8 включительно, то есть следующие цифры: 1, 2, 3, 4, 5, 6, 7 и 8. Если указана запись в виде (1;4), то ее нужно трактовать таким образом: от 1 не включительно до 4 не включительно, то есть в интервал входят только числа 2 и 3.
Для определения величины D (z) необходимо решить неравенство, корнем которого являются все значения аргумента. Для этих целей можно использовать и специализированное программное обеспечение. Математики рекомендуют свести пользование решебниками и программами к минимуму, поскольку не всегда предоставится возможность воспользоваться ими на экзаменах или контрольных.
Основные виды
Исследование функции зависит от ее вида, который нужно правильно определять. Для начала следует обозначить сложность, поскольку от этого параметра зависят дальнейшие действия и свойства, которыми придется руководствоваться. Математики производят разделение таким образом:
Алгебраические делятся на рациональные (без корня) и иррациональные (наличие радикала). Первые состоят из целых и дробных. D (z) для этих типов — все множество действительных чисел. Если функция представлена в виде обыкновенной дроби, то значение аргумента, приводящее к пустому множеству (знаменатель равен нулю), нужно исключить. Когда аргумент находится под знаком радикала (корня), тогда она считается иррациональной. Однако следует проверить, чтобы под корнем четной степени не было отрицательного значения, которое приводит к неопределенности.
Все функции, содержащие sin, cos, tg и ctg, являются тригонометрическими. Кроме того, arcsin, arccos, arctg и arcctg — обратные тригонометрические. Трансцендентные можно разделить на такие три группы: показательные, степенные и логарифмические.
Второе отличается от первого формулой. Другой тип классификации основан на периодичности. В зависимость от этого параметра все функции делятся на периодические и непериодические. Параметр периодичности означает повторение ее поведения через определенный период Т.
Существует еще один критерий. Он называется монотонностью. В зависимости от него, функции бывают монотонными и немонотонными. Первая группа характеризуется постоянностью, то есть она либо убывает, либо возрастает. Все остальные могут убывать и возрастать на определенных промежутках. Примером является y = cos (x), поскольку она является убывающей и возрастающей через определенный период.
Правила для выявления
Для того чтобы исследовать на четность, существует два правила или теоремы, которые записываются в виде двух формул. Четная — функция вида w (x), для которой справедливо такое равенство: w (-x) = w (x). Для нечетной соотношение немного другое: w (-x) = w (x). Однако бывают выражения, к которым не применимы эти тождества. Они принадлежат общему виду.
Для оптимизации решения специалисты рекомендуют использовать некоторую последовательность действий или специальный алгоритм. Он позволяет определить четность за минимальный промежуток времени и без ошибок. Необходимо обратить внимание на пункты или шаги, по которым выполняется подробная оценка:
Следствия из утверждений
Свойства или следствия из утверждений расчетов позволяют оптимизировать процесс решения, поскольку нет необходимости выполнять какие-либо действия. Очень часто приходится тратить много времени на задание, которое можно решить за несколько минут. Математики выделяют следующие свойства для таких функций:
Второе свойство можно записать математически таким образом: z (x) = y (x) + w (x). Выражение y (x) можно выразить следующим образом: y (x) = [z (x) — z (-x)] /2. Тождество w (x) выражается через z (x) формулой: w (x) = [z (x) + z (-x)] /2.
Классификация по четности
Специалисты давно уже исследовали некоторые функции. Примеры четных и нечетных можно классифицировать по признаку четности. Эти данные значительно ускоряют процесс анализа любого выражения. К нечетным функциям относятся следующие (следует учитывать, что аргумент «x» принадлежит множеству действительных чисел Z):
Кроме того, существуют еще составные выражения, элементами которых являются простые функции. Для анализа необходимо руководствоваться свойствами. Следующий класс, который объединяет все четные выражения, состоит из следующего перечня:
Остальные составляют класс общего вида, который не принадлежит к четным и нечетным. При решении задач необходимо иметь таблицу всех функций, которая должна быть составлена перед обучением. Следует учитывать, что на экзаменах и контрольных функции, используемые для описания каких-либо процессов, практически не исследуются. Зная алгоритм, не составит особого труда проверить выражение на четность. Следующим этапом, который поможет закрепить теоретические знания, считается практика.
Пример решения
Задачи исследования функции на четность встречаются редко, поскольку этот элемент входит в полный анализ ее поведения. Пусть дано тождество z (y) = (y 2 — y — 2) / (y 2 — 1). В этом случае следует действовать по алгоритму:
Задачу можно решить вторым способом — проанализировать составляющие элементы. Например, знаменатель всегда будет нечетным, поскольку от четного y 2 отнимается нечетное число (6 — 1 = 5). Этот способ используется в некоторых языках программирования, для написания подпрограмм и процедур, позволяющих проверить или отобрать все нечетные значения. Числитель также является нечетным, поскольку он содержит нечетный элемент «y». Если построить график, используя любой из веб-ресурсов, то он окажется симметричным относительно начала координат.
Первое свойство свидетельствует о том, что функция является нечетной. Некоторые новички делают распространенную ошибку, считая, что отношение нечетных есть величина четная. Однако такое утверждение не применимо в этом случае. Если бы было произведение двух нечетных выражений, то результат являлся бы четным. Об этой особенности свидетельствует свойство под номером 4.
Таким образом, для исследования функции на предмет ее четности или нечетности нужно воспользоваться специальным алгоритмом, который рекомендуют математики. Он позволит выполнить операцию без ошибок и за короткий промежуток времени.
Исследовательская работа по теме: «Четность произведения двух функций»
Муниципальное образовательное учреждение
средняя общеобразовательная школа №129
Советского района Волгограда
Исследовательская работа по теме:
«Четность произведения двух функций»
обучающиеся 8 «Б» класса
Иванас Ирина Анатольевна,
Глава 1. Теоретическая подготовка и сбор материала исследования. 5
Сбор первичного фонда информации. 5
Классификация фонда. 5
Составление модели для исследования. 6
Сбор дополнительного фонда для того, чтобы можно было
исследовать все виды моделей. 6
Глава 2. Исследование собранного материала. 7
2.1. Исследование полученных моделей на четность
(по выбранному вопросу). 7
Глава 3. Гипотеза и ее проверка на практических примерах. 8
3.1. Формулировка гипотезы. 8
3.2. Проверка гипотезы на дополнительном фонде. 8
Глава 4. Обобщенная формулировка гипотезы и её теоретическое обоснование. 9
4.1. Формулировка гипотезы в виде теорем (если…, то…). 9
4.2. Доказательство теоремы в общем виде. 9
Список литературы 12
Проблема. Четность произведения двух функций.
изучение алгоритма определения четности произведения двух функций;
содействие углублению теоретического материала;
развитие познавательного интереса, расширение представления о свойствах произведения двух функций;
развитие умения осуществлять самостоятельный поиск информации, анализировать и обобщать её.
расширить знания программного материала о четности функции;
продолжить формирование умения исследовать функцию на четность с помощью определения;
формировать культуру построения графиков функций, культуру формулирования новой гипотезы и её доказательства;
развивать способность к исследовательской и проектной деятельности;
повысить информационную и коммуникативную компетентность.
расширение знаний о четности функции, четности произведения двух функций;
развитие средствами составления гипотез и их доказательства своих индивидуальных способностей и своего саморазвития;
умение использовать новую информацию и дополнительную литературу, выполнять анализ полученного материала и синтезировать его в доказательстве гипотезы.
Объектная область : математика.
Объект исследования: функции.
Предмет исследования : четность функции.
метод визуализации данных.
Новизна и практическое значение:
Изучая свойства элементарных функций (линейная, квадратичная, степень с натуральным показателем, обратная пропорциональность, модуль), мы узнали, как исследовать функцию на четность по определению. Изучаемые в школьной программе функции были исследованы нами на четность. В данной работе с помощью теоретического материала и графиков функций исследована четность произведения двух функций, что способствует углублению знаний и расширению кругозора.
Глава 1. Теоретическая подготовка и сбор материала исследования.
Изучая теоретический материал по теме «Функции и их свойства мы
познакомились со свойством четности.
По определению, которое мы нашли в дополнительной литературе,
четной называется функция f(x), обладающая следующими свойствами:
1). Область определения функции (D(f)) симметрична относительно начала отсчета;
Сбор первичного фонда информации.
Из собственного опыта мы собрали копилку конкретных примеров функций, известных из курса алгебры:
y=5x; y=-7x+5; y=x 2 ; y=x 3 ; y=x 4 ; y=x 5 ; y=|x|; y=3/x; y=5; y=x; y=5x 2 +2x-3
На этом этапе мы провели классификацию собранного фонда функций по четности.
Составление модели для исследования.
Для четности произведения двух функций, четность которых известна, возможны варианты:
Ч 
Ч 
Н 
Сбор дополнительного фонда для того, чтобы можно было исследовать все виды моделей.
у=5х 
у= х 5 
у=х 
Глава 2. Исследование собранного материала.
2.1. Исследование полученных моделей на четность (по выбранному вопросу).
2). z (- x ) = (- x ) 2 
2). f (- x ) = (- x ) 
Глава 3. Гипотеза и ее проверка на практических примерах.
3.1. Формулировка гипотезы.
В первом случае: Ч 
Во втором случае: Ч 
В третьем случае: Н 
3.2. Проверка гипотезы на дополнительном фонде.
2). у(х)=|x| 
2). у(-x) =|-x| 

3). у(х)= х 5 
2). у(-x) =(-x) 5 

Глава 4. Обобщенная формулировка гипотезы и её теоретическое обоснование.
4.1. Формулировка гипотезы в виде теорем (если…, то…).
1). Если перемножить две четные функции, то в результате получится четная функция.
2). Если перемножить четную и нечетную функции, то в результате получится нечетная функция.
3). Если перемножить две нечетные функции, то в результате получится четная функция.
4.2. Доказательство теоремы в общем виде.
1). Если перемножить две четные функции, то в результате получится четная функция.
2). Если перемножить четную и нечетную функции, то в результате получится нечетная функция.
3). Если перемножить две нечетные функции, то в результате получится четная функция.
Изучив теоретический материал, рассмотрев свойство четности элементарных функций, мы исследовали четность произведения двух функций, четность которых была нам уже известна. Работая над этой темой мы выяснили, что произведение двух четных функций и двух нечетных функций есть четная функция, а произведение четной функции и нечетной функции есть нечетная функция.
При помощи определения четности функции нам удалось провести исследование частных примеров, затем проверить и доказать гипотезу четности и нечетности произведения двух функций.
Изучение данной проблемы помогло нам выбрать дальнейший путь исследований.
Нами были определены следующие направления работы:
увеличить фонд за счет добавления более сложных функций. Здесь можно доказать теорему о том, что произведение любого количества четных функций есть функция четная (Ч 



рассмотреть частные случаи (отыскание возможных следствий из доказанной теоремы);
составить и проверить обратные утверждения.
Полученные знания и умения сбора и анализа материала, составления гипотезы и доказательства её помогут нам провести исследование по выбранному направлению.
Урок алгебры «Четность и нечетность функции» (11 класс)
Муниципальное бюджетное общеобразовательное учреждение средняя
рабочего посёлка Мухен муниципального района имени Лазо Хабаровского края
Четность (нечетность) функции
Кушнарь Лариса Александровна
Тема урока: Четность (нечетность) функции.
Тип урока, форма : урок итогового повторения, урок подготовки к ЕГЭ.
Учебная задача урока: Обобщить и систематизировать знания по теме «Четность (нечетность) функций» для подготовки учащихся к ЕГЭ по алгебре на основе анализа заданий типа А и В, свойственных для ЕГЭ.
В результате ученик:
— определение четной (нечетной) функции;
— как по графику функции определить является функция четной, нечетной или функцией общего вида;
— как по аналитическому заданию функции определить является ли она четной, нечетной или функцией общего вида;
— частные виды четных (нечетных) функций;
— сумма четных ( нечетных) функций есть функция четная (нечетная);
— произведение четных (нечетных) функций есть четная функция;
— произведение четной и нечетной функции есть нечетная функция;
— если внешняя функция действует на четную функцию, то композиция этих функций есть функция четная.
— по аналитическому и графическому заданиям функций определять является функция четной, нечетной или функцией общего вида;
— решать задачи на применение определения и свойств четной (нечетной) функции;
— что график четной функции симметричен относительно оси Оу, а график нечетной функции – относительно начала координат.
Ученикам выдается раздаточный материал, на котором в разброс изображены графики четных, нечетных функций и функций общего вида..
— Перед вами несколько графиков функций. На какие группы можно разбить эти графики?
(1 группа: графики симметричные относительно оси Оу;
2 группа: графики симметричные относительно начала координат;
3 группа: оставшиеся.)
— Какое свойство функции говорит нам о симметрии относительно оси ординат? Начала координат?
— Запишите тему нашего сегоднешнего урока: « Четные и нечетные функции».
-Вспомните определение четной (нечетной) функции.
— Запишите данное определение в таблицу.
— В какой из выделенных вами групп находятся графики четных функций? Нечетных? Функций общего вида?
— Чем вы руководствовались при выполнении этого задания?
( определением четной и нечетной функции)
— Сформулируйте правило по которому по графику функции можно определить к какому типу функции принадлежит этот график.
( если график функции симметричен относительно оси ординат, то функция четная, если график функции симметричен относительно начала координат, то функция нечетная)
— Запишите это правило в таблицу.
— какой вывод можно сделать об областях определения четных и нечетных функций?
(для любой четной или нечетной функции областью определения может являться только такое множество, для которого оба числа х и – х либо одновременно входят в область определения функции, либо одновременно не входят в область определения).
— Сконструируйте несколько множеств, которые могут быть областью определения четных или нечетных функций.
— Хорошо. Теперь начертите 4 системы координат, пронумеровав их цифрами 1,2, 3,4. Изобразите в них графики четырех функций так, чтобы одна из них являлась функцией четной, другая – нечетной, а третья – функцией общего вида. На оставшейся системе координат начертите произвольный график функции. Попросите соседа по парте определить номер графика, соответствующего функции четной, функции нечетной, а также функции общего вида.

— Определите является функция четной, нечетной или функцией общего вида:
в) f ( x ) = x 3 + 5 sinx ;
— Постройте алгоритм определения четности 9нечетности функции по ее аналитическому заданию.
1) проверить симметричность области определения функции. Если не симметрична, то функция общего вида
3)сравнить f (- x ) и f ( x ):
а) f (- x ) = f ( x ), то четная;
— Запишите этот алгоритм в таблицу.
( так как функция четная, то ее график будет симметричен относительно оис ординат, то есть достаточно построить график при х ≥ 0 и отразить его симметрично относительно Оу.
Далее учитель разбивает класс на 10 групп. Каждая группа получает индивидуальное задание.
1 группа: определить четной или нечетной является функция, полученная в результате суммы (разности)двух четных функций;
2 группа: определить четной или нечетной является функция, полученная в результате суммы (разности) двух нечетных функций;
3 группа: определить четной или нечетной является функция, полученная в результате суммы (разности) четной и нечетной функции;
4 группа: определить четной или нечетной является функция, полученная в результате произведения(частного) двух четных функций;
5 группа: определить четной или нечетной является функция, полученная в результате произведения (частного) двух нечетных функций;
6 группа: определить четной или нечетной является функция, полученная в результате произведения(частного) четной и нечетной функции;
7 группа: определить четной или нечетной является функция, полученная как композиция двух четных функций;
8 группа : определить четной или нечетной является функция, полученная как композиций четной и нечетной функции;
9 группа: определить четной или нечетной является функция, полученная как композиция нечетной и четной функции;
10 группа: определить четной или нечетной является функция, полученная как композиция двух нечетных функций.
Через 5 минут проверяем и делаем выводы:
Сумма и разность нечетных функций – нечетные функции, а произведение и частное двух нечетных функций (кроме деления на 0) – четные функции;
Сумма, разность, произведение и частное (кроме деления на 0) четных функций – четные функции;
Если в композиции обе функции нечетные, то функция будет нечетной, во всех остальных случаях получаем четную функцию.
В конце урока предлагаем ученикам выполнить небольшой тест:
1) Среди предложенных функций выберите четную:
2) На одном из следующих рисунков изображен график нечетной функции. Укажите этот рисунок.
3)Непрерывная нечетная функция f ( x ), определенная на всей числовой оси, на промежутке (0; +∞) обращается в 0 в четырех точках. Найдите число корней уравнения f ( x ) = 0 на промежутке (-∞; +∞).
Приведите примеры четных и нечетных функций. Докажите, что приведенные вами функции являются четными или не четными.
Приведите примеры функций, которые не являются четными и не являются нечетными из-за того, что область определения несимметрична относительно точки О.
Постройте график функции f , если при х≤0 значения функции находятся по формуле у = х +4 и известно, что функция f – четная.