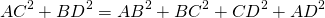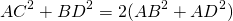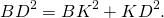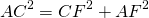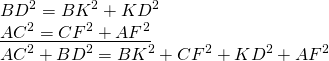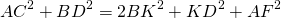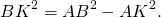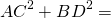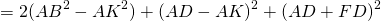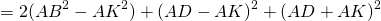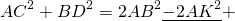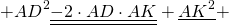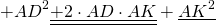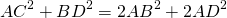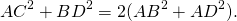Докажите что сумма квадратов диагоналей параллелограмма равна

Сумма квадратов диагоналей параллелограмма

Теорема. (Свойства диагоналей параллелограмма).

Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Так как противолежащие стороны параллелограмма равны: AB=CD, AD=BC, то сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон:

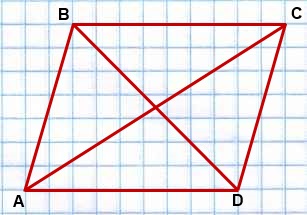
AC и BD — диагонали.

1) Опустим перпендикуляры BK и CF на прямую, содержащую сторону AD.

2) Рассмотрим прямоугольный треугольник BDK.

По теореме Пифагора

3) Аналогично, из прямоугольного треугольника ACF

4) Сложим почленно полученные равенства:

BK=CF (как высоты параллелограмма, проведенные к одной стороне), поэтому

5) Из прямоугольного треугольника ABK по теореме Пифагора

6) KD=AD-AK, AF=AD+FD, поэтому

7) BK=CF, AB=CD. Значит, прямоугольные треугольники ABK и DCF равны (по катету и гипотенузе).

Следовательно, их соответствующие стороны равны: AK=DF. Отсюда,

Что и требовалось доказать.

Свойство диагоналей параллелограмма можно рассматривать как следствие из теоремы косинусов.

Этот способ доказательства будет рассмотрен в следующий раз.

2 Comments

почему 2ой способ не приведен?

В следующем посте. Следствия теоремы косинусов.

Источник

Как доказать, что сумма квадратов диагоналей параллелограмма равна суме квадратов его сторон?

Лучший ответ по мнению автора

Степин Александр

Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Так как противолежащие стороны параллелограмма равны: AB=CD, AD=BC, то сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон:

AC и BD — диагонали.

1) Опустим перпендикуляры BK и CF на прямую, содержащую сторону AD.

2) Рассмотрим прямоугольный треугольник BDK.

По теореме Пифагора

3) Аналогично, из прямоугольного треугольника ACF

4) Сложим почленно полученные равенства:

BK=CF (как высоты параллелограмма, проведенные к одной стороне), поэтому

5) Из прямоугольного треугольника ABK по теореме Пифагора

6) KD=AD-AK, AF=AD+FD, поэтому

7) BK=CF, AB=CD. Значит, прямоугольные треугольники ABK и DCF равны (по катету и гипотенузе).

Следовательно, их соответствующие стороны равны: AK=DF. Отсюда,

Источник

Как доказать, что сумма квадратов диагоналей параллелограмма равна суме квадратов его сторон?

Лучший ответ по мнению автора

Степин Александр

Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Так как противолежащие стороны параллелограмма равны: AB=CD, AD=BC, то сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон:

AC и BD — диагонали.

1) Опустим перпендикуляры BK и CF на прямую, содержащую сторону AD.

2) Рассмотрим прямоугольный треугольник BDK.

По теореме Пифагора

3) Аналогично, из прямоугольного треугольника ACF

4) Сложим почленно полученные равенства:

BK=CF (как высоты параллелограмма, проведенные к одной стороне), поэтому

5) Из прямоугольного треугольника ABK по теореме Пифагора

6) KD=AD-AK, AF=AD+FD, поэтому

7) BK=CF, AB=CD. Значит, прямоугольные треугольники ABK и DCF равны (по катету и гипотенузе).

Следовательно, их соответствующие стороны равны: AK=DF. Отсюда,

Источник

Параллелограмм: свойства и признаки

Определение параллелограмма

Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Как выглядит параллелограмм:

Частные случаи параллелограмма: ромб, прямоугольник, квадрат.

Диагонали — отрезки, которые соединяют противоположные вершины.

Свойства диагоналей параллелограмма:

Биссектриса параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.

Свойства биссектрисы параллелограмма:

Как найти площадь параллелограмма:

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!

Свойства параллелограмма

Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.

Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:

А сейчас докажем теорему, которая основана на первых двух свойствах.

Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.

В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.

Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:

Теорема доказана. Наше предположение верно.

Признаки параллелограмма

Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.

Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Докажем 1 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.

Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.

Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:

Шаг 3. Из равенства треугольников также следует:

Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.

Вот так быстро мы доказали первый признак.

Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

Докажем 2 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:

Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.

Шаг 3. Из равенства треугольников следует:

А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.

Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.

Доказали второй признак.

Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Докажем 3 признак параллелограмма:

Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:

Шаг 2. Из равенства треугольников следует, что CD = AB.

Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).

Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.

Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.

Источник

Применение теоремы Вариньона к решению задач

2. 2. Применение теоремы Вариньона к решению задач.

Рассмотрим применение теоремы Вариньона к решению планиметрических задач повышенной трудности. Дело в том, что планиметрические задачи на олимпиадах встречаются значительно чаще.

Задача 1. В выпуклом пятиугольнике ABCDE середины сторон AB и CD, BC и DE соединены отрезками. K, L – середины этих отрезков. Доказать, что отрезок KL параллелен пятой стороне AE и составляет ¼ от неё.

Решение: отрежем четырёхугольник ABCD и пусть Р-середина AD, тогда по теореме Вариньона A1B1C1P – параллелограмм, А1С1 – его диагональ и К – середина А1С1, значит, К – середина и второй

диагонали параллелограмма В1Р. Значит, KL – средняя линия треугольника PB1D1, поэтому KL||PD1 и KL=1/2 PD1, но PD1 – средняя линия треугольника ADE, значит, PD1||AE и PD1=1/2AE, поэтому KL||AE и KL=1/4 AE.

Задача 2. Верно ли, что можно составить треугольник из любой средней линии треугольника и отрезков, вдвое меньших его диагоналей?

Решение: верно, так как параллелограмм Вариньона существует для любого выпуклого четырёхугольника. Например, условию задачи удовлетворяют треугольники KLM и LMN на рис. 10. рис. 10

Задача 3. Средние линии четырёхугольника ABCD равны a и b, а угол между ними 60˚. Найдите диагонали четырёхугольника.

Решение: пусть KM=a, LN=b, (рис. 10). Тогда NM=, а LT=.

Из треугольника LTM по теореме косинусов . Но LM= BD, поэтому , откуда BD=. Аналогично из треугольника TNM найдём MN, потом вычислим AC: AC=.

Ответ: ;

Задача 4. Докажите, что сумма квадратов диагоналей четырёхугольника в два раза больше суммы квадратов его средних линий.

Доказательство: в параллелограмме Вариньона, как и в любом другом параллелограмме, сумма квадратов рис. 11 диагоналей равна сумме квадратов всех его сторон, т. е. Учитывая, что KL=1/2 AC и LM= 1/2 BD (рис. 11), получим: KM2+LN2=1/2(AC2+BD2), AC2+BD2=2(KM2+LN2).

Задача 5. Докажите, что площадь параллелограмма Вариньона равна половине площади четырёхугольника ABCD.

Доказательство: (рис. 12).

Учитывая, что , KL=1/2 AC и KN=1/2 BD, получим: рис. 12

.

Задача 6. Докажите, что все четырёхугольники, имеющие общие середины

Доказательство: действительно, для всех таких четырёхугольников определён один и тот же параллелограмм Вариньона. Его площадь равна половине площади каждого из исходных четырёхугольников (задача 5), тем самым их равновеликость доказана.

Задача 7. Докажите, что если диагонали четырёхугольника равны, то его площадь равна произведению средних линий.

Доказательство: в случае равенства диагоналей AC и BD параллелограмм Вариньона KLMN является ромбом (рис. 13), а рис. 13

площадь ромба равна половине произведения диагоналей:

, тогда .

Задача 8. Диагонали четырёхугольника ABCD равны d1 и d2, а средние линии равны между собой. Найдите площадь четырёхугольника.

Решение: из условия задачи следует, что в параллелограмме Вариньона диагонали KM и LN равны (рис. 12). Значит, KLMN – прямоугольник и SKLMN=1/2 d1d2, а с другой стороны, SKLMN=1/2 SABCD, следовательно, SABCD=1/2d1d2.

Ответ: SABCD=1/2d1d2.

Задача 9. Докажите, что площадь четырёхугольника равна произведению средней линии на одну из диагоналей и на синус угла между ними.

Доказательство: согласно рис. 14 необходимо доказать, рис. 14

что . Треугольник KLN представляет собой половину параллелограмма Вариньона. (). Так как KL=1/2AC, то , значит, , а с другой стороны, (см. задачу 8), тогда .

Задача 10. Докажите, что сумма квадратов сторон четырёхугольника равна сумме квадратов его диагоналей, сложенной с учетверённым квадратом отрезка, соединяющего середину его диагоналей.

Доказательство: согласно рис. 11 надо доказать, что. Для медианы ET треугольника ELN имеем: , где , , откуда . Аналогично, выразив медиану FT треугольника KFM и учитывая, что и , получим: .

Кроме того, (задача 7).

Итак, получаем: , откуда:

Задача 11. Постройте трапецию по диагоналям, одному из углов и отрезку, соединяющему середины оснований.

Решение: пусть в трапеции ABCD, которую необходимо построить, известны длины диагоналей AC и BD, отрезка LN и величина угла А (рис. 15).

Поскольку и , нетрудно построить по трём рис. 15

сторонам треугольник KLN. Далее построим его до параллелограмма Вариньона. Затем на отрезке KN построим сегмент, вмещающий угол А, и проведём через точку N параллельно KM прямую, она пересечёт сегмент в точке А. Дальнейшее построение очевидно.

В ходе работы мы прорешали более двадцати пяти задач, формулировки и решения наиболее интересных из них дополнительно приведены в приложении. Мы убедились в том, что теорема Вариньона помогает красиво, оригинально решать задачи, открывать и доказывать новые свойства четырёхугольников.

Источник